钻井液连续波信号发生器控制方法

王正旭，房 军，裴科飞

(1.石油工程教育部重点实验室(中国石油大学(北京))，北京 102249；2.油气资源与工程国家重点实验室(中国石油大学(北京))，北京 102249；3.广州特种承压设备检测研究院，广东广州510663)

钻井过程中，井下信息高效、快速传输是提高钻井效率的重要途径之一。与传统正脉冲传输方式相比,采用钻井液连续波信号传输井下信息具有更高的信息传输速率[1_4]。目前，Schlumberger公司已有相关产品并成功应用于钻井现场[5_6]，其井下信息传输速率达到10 b/s，而国内一直沿用传输速度较低的正脉冲传输技术，在连续波信号传输技术领域仍未取得实质性进展。房军等人[7_9]应用液压系统控制理论对往复式锥阀的信号发生器进行研究，建立了二通阀进液控制式信号发生器的数学模型;贾朋等人[10_14]分析了旋转阀式连续波信号发生器的水力特性，并设计了相关试验;WANG Zhengxu等人[15]对多排圆形往复阀口进行了优化设计，优化后的阀口能产生钻井液连续波，且相关系数达到0.998 3;房军等人[16]还对快速产生钻井液连续波信号发生器的往复主阀阀口形状及分布进行了研究。但是截至目前，对于往复式钻井液连续波信号发生器的控制机构及控制方法尚无相应的设计及特性分析。因此，在前人研究成果的基础上，笔者对驱动主阀运动的控制机构进行了设计，并对电动机控制特性及方法进行了研究，以期为钻井液连续波信号发生器的整体设计及其现场应用提供参考。

1 连续波信号产生机理及其控制机构

1.1 连续波信号产生机理

钻井液连续波信号发生器主要由主阀、往复轴和控制机构组成[16]，如图1所示。控制机构首先将电动机的旋转运动转化为往复轴的往复运动，然后往复轴驱动主阀对流过主阀的钻井液产生节流作用。在主阀往复运动1个周期内，钻井液出现不同程度的局部水力损失，最终产生压力波动信号。

图1 连续波信号发生器结构Fig.1 Structure of the continuous wave signal generator

对信号发生器来说，产生的液压信号特性主要受阀口形状及控制机构驱动规律的影响[15,17]。同时，控制机构也是产生信号最重要的动力来源，因此主要从控制机构和控制方法2方面进行研究，以实现钻井液连续波传递井下信息，最终为连续波信号发生器控制机构的设计及特性分析提供指导。

1.2 斜面凸轮机构

斜面凸轮机构以其结构简单、易于加工的特点，被优选为连续波信号发生器的控制机构。它主要由推杆、斜面凸轮、调心球轴承、推力球轴承和传动轴组成，如图2所示。其中，斜面凸轮的凸轮面为斜面，且斜面上可以有1个或2个推杆。当斜面凸轮从图2位置开始旋转，经过半个周期，右边的推杆从位移最小点运动至位移最大点，继续旋转半个周期，右边推杆恢复至初始位置。可见，斜面凸轮旋转的周期和推杆往复运动周期是相同的。

图2 双推杆斜面凸轮机构Fig.2 Beveled cam actuator with double push rods

斜面凸轮机构中，推杆的运动规律与凸轮面倾斜角度、转速和有效直径有关。斜面凸轮的简化模型如图3所示。由于推杆的直径较小，在计算过程中可以忽略。斜面凸轮推动推杆的有效直径为D，凸轮面倾角为α。推杆起始时位于t=0时刻的位置，此时推杆位移为0。由于主阀受到液压的作用，斜面凸轮在旋转过程中，推杆始终与凸轮斜面保持接触。当凸轮以角速度ω旋转、历经时间t、旋转角度为θ时，推杆的位移为h。

图3 斜面凸轮简化模型Fig.3 Simplified model of beveled cam

由几何关系推导出推杆的位移h与斜面凸轮旋转角度θ之间的关系：

(1)

其中θ=ωt

(2)

式中：h为推杆的位移，m；D为斜面凸轮的有效直径，m；α为斜面凸轮的斜面倾角，(°)；θ为电动机旋转的角度，rad；ω为凸轮旋转角速度，rad/s；t为凸轮旋转时间，s。

对式(1)求导，得到推杆往复运动的速度随时间的变化关系：

(3)

式中：v为推杆运动的速度，m/s。

2 连续波信号发生器控制分析

斜面凸轮的旋转由电动机提供力矩，对电动机进行调速可以产生特定规律的钻井液压力波，因此需要对电动机的运行特性及控制方法进行研究，以实现传输井下信息的目的。

主阀的往复运动是通过电动机正反转来实现的，所以电动机的旋转是变速的。同时，在产生正弦连续波的过程中，也需要电动机变速旋转，若电动机匀速旋转驱动推杆匀速运动时，主阀产生的液压脉冲波不是正弦连续波[17]。经过筛选，选择经济性能较好的普通无刷直流电动机，它具有运行效率高、调速性能好、运行顺畅、寿命长和维护成本低等优点[18]。井下使用过程中，需要对其进行特殊密封设计，以保证其正常工作及延长使用寿命。井下复杂的工作环境对电动机的工作性能有苛刻的要求，优选电动机性能参数是顺利产生连续波信号的保证。

2.1 无刷直流电动机调速方法

根据机电传动控制理论[19]，他励直流电动机的机械特性表达式为：

(4)

式中：n为电动机的转速，r/min；U为直流电动机的供电电压，V；Φ为一对磁极的磁通量，Wb；Ra为电枢电阻，Ω；Rad为电枢电路的外加电阻，Ω；T为电磁转矩，N·m；Ke和Kt为电动机的电势常数，Kt=9.55Ke。

从式(4)可知，电动机的调速方法有3种，分别为改变电枢电路内的外加电阻Rad、电枢供电电压U或磁通量Φ。改变电枢供电电压可以实现平滑无极调速，且电动机的机械特性硬度不变，调速范围大，因此，本文选择通过改变电枢电压的方式来实现调速。

2.2 电动机转速分析

假设主阀产生钻井液正弦连续波，则根据阀口流量压力特性方程可以得出主阀运动规律，从而推导出电动机转速随时间的变化关系。

钻井液正弦波波形曲线方程为[16]：

Δp=asin(ω0t+φ)+b

(5)

(6)

(7)

式中：Δp为钻井液正弦压力波，MPa；Δpmax和Δpmin分别为预期最大和最小压差，MPa；φ为正弦压力曲线的初始相位，rad；ω0为预期正弦压力曲线的角速度，rad/s。

ω0的表达式为：

(8)

式中：T0为正弦压力波曲线的周期，s；f0为正弦压力波曲线的频率，Hz。

连续波信号发生器阀口的流量压力特性方程为[20]：

(9)

式中：Q为钻井液流量，m3/s；Cd为阀口的流量系数；ρ为钻井液密度，kg/m3；Δp为阀口前后压差，MPa；A为阀口通流面积，m2。

阀口通流面积计算式为[17]：

A=m1m2(L-x)W+A0

(10)

式中：L为单个矩形阀口的长度，m；x为主阀的位移，m；W为单个矩形阀口的宽度，m；A0为预留阀口的面积，m2；m1为阀口沿径向分布数量；m2为阀口沿周向分布数量。

由于推杆驱动主阀运动，推杆位移与主阀位移相等。联立式(1)、式(5)、式(9)和式(10)，得到电动机转角的表达式：

电动机的转速可表达为：

(12)

将式(11)代入式(12),即得到电动机转速n与时间t的关系式。

2.3 电动机负载转矩分析

在电动机旋转驱动推杆往复运动过程中，对电动机负载转矩的定量分析是电动机顺利调速的保证。对斜面凸轮在旋转过程中进行受力分析,结果如图4所示。这里只考虑斜面凸轮与推杆接触面的摩擦作用。由于主阀受到的液压力要远远大于推杆的重力，因此推杆重力可以忽略。

图4 斜面凸轮受力分析Fig.4 Force analysis of beveled cam

根据对斜面凸轮的受力分析，可得电动机的负载转矩表达式为：

(13)

其中F0=μF1cos2α

(14)

式中：T为电动机的负载转矩，N·m；F0为凸轮旋转所需的力，N；F1为推杆受到的力，N；μ为凸轮斜面与推杆接触面的摩擦系数。

由于推杆和主阀连接，推杆受到的力F1等于主阀受力，因此结合式(5)可将推杆受力表示为：

(15)

式中：d为主阀直径，m。

将式(14)和式(15)代入式(13)，得到电动机负载转矩T随时间t的变化关系：

(16)

最后，将式(11)、式(12)和式(16)代入式(4)，令Rad=0，便得到电动机电枢电压U随时间t的变化关系。

3 算例分析

本文研究的钻井液连续波信号发生器控制方法主要是为文献[17]中的试验主阀提供驱动力，从而实现产生钻井液连续波的目的。已知主阀参数、斜面凸轮参数、正弦连续压力波参数和无刷直流电动机参数，分析电动机转角、转速、负载转矩和电枢电压等控制特性随时间的变化情况。

主阀参数[17]：阀口沿径向分布3排、周向对称分布2个，单个矩形阀口长度6 mm、宽度24 mm，主阀有效直径为6 mm，阀口预留面积为9×10-5m2，阀口流量系数为0.6，钻井液流量为250 L/min，钻井液密度为1.0 kg/L，不考虑钻井液黏度等因素对压力波信号的影响。

斜面凸轮参数：有效直径为40 mm，斜面倾角为13°，推杆与凸轮面之间的摩擦系数为0.05。

无刷直流电动机参数：额定电压为24 V,额定电流为1.6 A,额定转速为3 000 r/min,空载转速4 000 r/min,额定力矩为0.08 N·m,电动机内阻为3 Ω[18],ΦKe和ΦKt分别为0.006 4和0.061 0。

通过计算式(11)和式(12)，得到电动机转角和转速随时间的变化规律，分别见图5和图6。

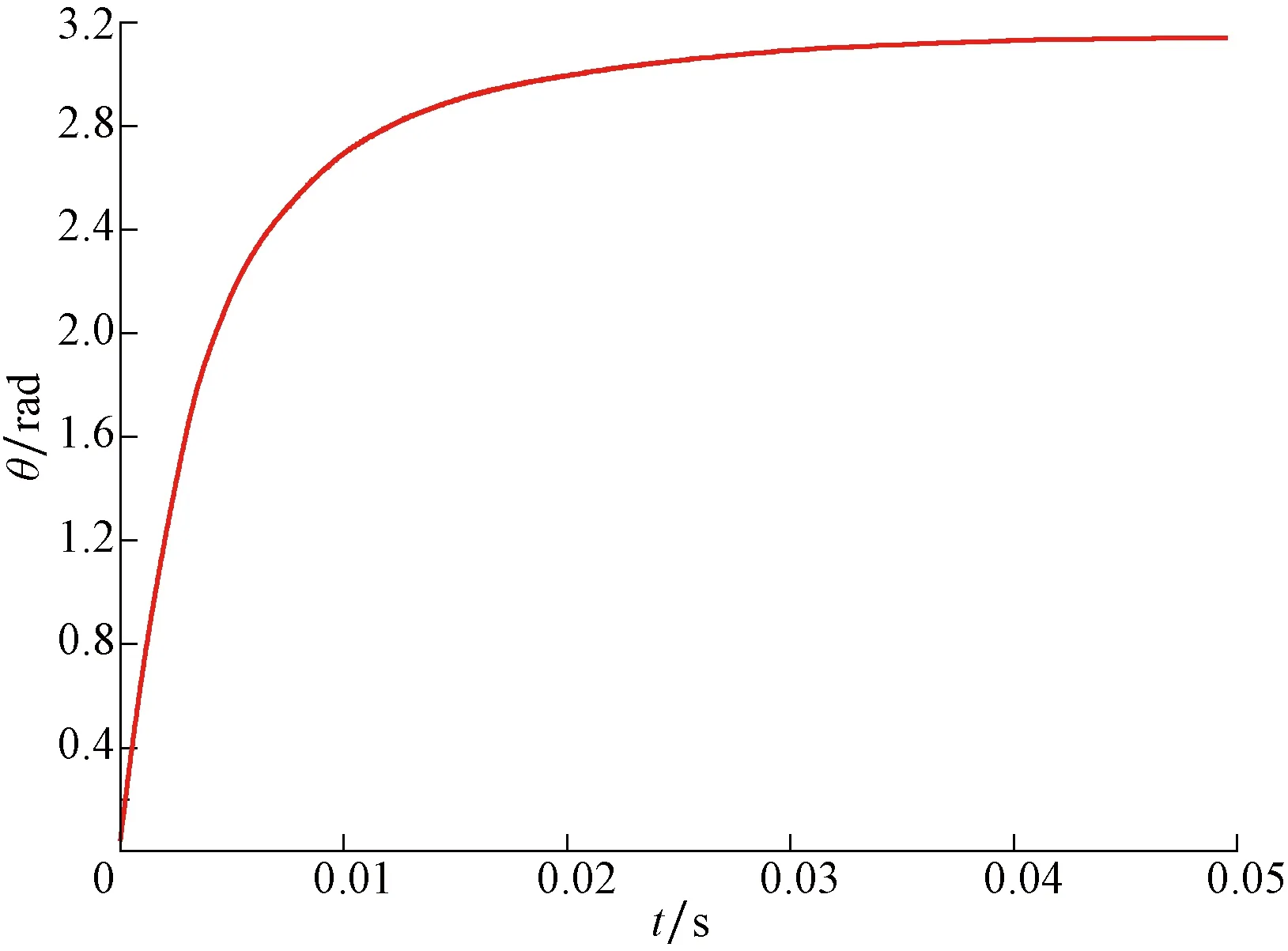
图5 电动机转角随时间的变化曲线Fig.5 Variation curve of motor rotary angle with time

由图5、图6可知，在推杆驱动主阀往复运动过程中，阀口开始被关闭时，凸轮即将旋转，此时转角为0，电动机转速产生阶跃变化，电动机转速最大为3 334 r/min；随着凸轮旋转，阀口逐渐关闭，电动机转角非线性增加，电动机转速开始下降，直到完全关闭阀口，电动机停止转动，以上过程只持续了半个周期；同样，当主阀从最大位移处反向运动时，电动机开始反向转动，直至主阀恢复到初始位置。重复以上运动过程，便产生了正弦连续压力波。

图6 电动机转速随时间的变化曲线Fig.6 Variation curve of motor rotary speed with time

根据式(16)，可得到电动机旋转过程中的负载转矩变化曲线，如图7所示。由图7可知，转矩呈非线性增加的趋势，当主阀完全关闭阀口时受到的液压力是最大的，其转矩也达到最大，符合实际情况，此时电动机的最大负载转矩Tmax为0.46 N·m。

图7 电动机负载转矩随时间的变化曲线Fig.7 Variation curve of motor load torque with time

电动机电枢电压随时间的变化曲线见图8。

图8 电动机电枢电压随时间的变化曲线Fig.8 Variation curve of motor armature voltage with time

从图8可以看出，根据电动机电压变化规律，可以控制主阀产生钻井液正弦连续压力波。

以上对电动机控制特性的计算是在产生某一恒定频率连续波的条件下进行的。 要将井下信息传输至地面,需要对压力波信号进行调频。 笔者运用Huffman编码形式来控制电动机以产生不同频率的连续波，然后根据2种不同频率波形的交替变化传递钻井参数信息。

Huffman编码是1个二进制的编码，算例分析中设定的正弦压力波的频率为10 Hz，用1代表这个频率，再产生1个频率为5 Hz，用0代表这个频率，通过0和1编码传递信息。

例如，要传输的数据是55.8°井斜角和118.3°方位角，数据报表格式为：

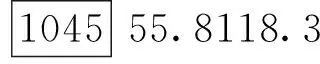
Huffman编码形式为[21]：

截取其中一段编码(110010)对电动机进行调制，调制过程中钻井液连续压力波变化曲线、电动机转速和电压的变化曲线见图9。该示例表明，通过调节电动机转速可以产生钻井液连续压力波，对连续波调频可以实现井下信息的传输。

图9 电动机编码调制图Fig.9 Motor code modulation diagram

4 结 论

1) 斜面凸轮机构不仅具有结构简单、易于加工的优势，而且能够将电动机的旋转运动转化为主阀的往复运动，满足连续波信号发生器的使用要求。

2) 利用建立的电动机转速、负载转矩及电枢电压计算模型，可以定量分析产生钻井液连续波的电动机特性，为优选电动机提供指导。

3) 算例分析表明，通过改变电枢电压的调速方法可以产生钻井液连续压力波，对连续波调频可以实现井下信息传输。

4) 提出的往复式钻井液连续波信号发生器的控制方法，可以为井下信号发生装置的设计提供理论指导。