“小数乘法”起点在哪儿

□ 郜舒竹

“小数乘法”作为小学数学课程内容，通常安排在五年级第一学期的第一单元。课程内容主要包括：竖式算法、乘积取近似数、应用运算律简便计算以及在实际情境中的应用。其中对于竖式算法的介绍，是将小数转化为整数，通过整数竖式计算的方法计算小数乘法。这样的安排试图将整数乘法的方法直接应用于小数乘法运算。

这样安排的问题在于，两个小数相乘已经失去了“相同加数求和”的含义。对于一个算式，如果仅知道怎样算，不知道何时这样算，显然是计算教学的缺失。因此学习小数乘法的起点不应当是怎样算的问题，而是如何理解两个小数相乘的过程。

一、“乘”的本质是放缩

把两数相乘的过程视为相同加数求和，或者简称为“重复加（Repeated Addition）”，是认识乘法运算的初步阶段，这样的认识是以“数数（音：shǔ shù；英：Counting）”的活动为基础的。比如，某商品每千克3.5元，如果买3千克，需要多少元？实际就是求“3个3.5等于多少”，数数的思考过程可以用图1表示。

图1 “3个3.5”直观示意图

用加法算式表示出来就是：

3.5＋3.5＋3.5

由于重复加法可以表示为乘法，因此3个3.5可以写成乘法算式“3.5×3”。像这样将两数相乘的运算过程看作重复加，在两个因数都是小数的情况下，就无法解释其含义了。比如，某商品每千克3.5元，如果买0.5千克，需要多少元？

这时列出的算式“3.5×0.5”，就没有重复加的过程。因此在学习小数乘法之前，首先需要拓展对两个数相乘意义的理解。

事实上，题目中出现了两类不同的“变量（Vari⁃able）”，分别是“质量（Capacity）”和“价格（Price）”，二者具有“协变（Covariation）”的关系，也就是相互依赖、协同变化的关系。其中的变化，可能是变大，也可能是变小。

表格中把“1千克对应3.5×1元”看作变化的起点，如果质量从1千克扩大为3千克，那么价格就从3.5×1元，协同扩大为3.5×3元。同样，如果质量从1千克缩小为0.5千克，那么价格就从3.5×1元协同缩小为3.5×0.5元。

按照这样的理解，对于3.5×0.5的算法，首先想到的不是将3.5和0.5分别乘10，变为整数乘法算式35×5。而应当是0.5和1的关系，如果已经知道0.5是1的一半（或），那么接下来就要想3.5的一半（或）是多少？根据小数与整数的位值关系可以知道：

3.5＝3＋0.5

再根据对于分数的初步认识，可以知道3的一半是1.5，0.5的一半是0.25。所以可以得到3.5×0.5的结果为：

3.5× 0.5＝1.5＋0.25＝1.75

这样的思考过程叫作“比例思维（Proportional Thinking）”，实质上是将乘的过程看作是“放缩（Scaling）”的过程，也就是把乘的过程理解为放大或缩小的变化过程。

放缩的过程，不同于重复加的过程，本质上是基于“测量（Measure）”的认识活动。测量过程一般是源于比较的需要，主要包含两个基本要素，第一是确定标准（单位），第二是被测对象与标准的关系。前面题目中是将“3.5×1”视为标准，然后看3.5×3和3.5×0.5相对于标准发生了怎样的变化，前者是扩大为原来的3倍，后者缩小为原来的一半或二分之一。

依据这样的认识，乘的过程不仅是放大，而且可能缩小，更正了“越乘越大”的误解。放缩在数学中是类似于平移、旋转和对称的一种变换，主要描述某对象在原有状态下放大和缩小的规律。是将不同对象看作同一对象在一个变化过程中的不同状态。比如对于3×2，运用重复加的认识，可以看作是2条长度为3或者3条长度为2的线段的总长度。按照这样的认识，就无法解释算式0.3×0.2。

如果运用放缩变换的眼光看3×2，首先确定一条长度为1的线段，将其放大3倍，得到长度为3的线段，再将其放大2倍，这时线段的长度就是3×2。这样的方法同样可以应用于0.3×0.2。首先仍然是确定一条长度为1的线段，将其缩短为1的0.3倍得到长度为0.3的线段，再将其缩短0.2倍，这时线段长度就是0.3×0.2。用这样放缩变换的方法认识乘法，还可以解释对于长方形面积公式的困惑。

二、“长方形面积”的再认识

长方形面积公式的初步认识，通常安排在小学三年级第二学期数学课程中，认识的基本过程是利用小方格（面积单位）的行列关系，得到长方形面积等于长的长度与宽的宽度相乘（简称：长乘宽）。这样的认识，仍然是基于对两数相乘为重复加的理解，思考过程同样是以数数为基础的。只能将长方形面积公式的正确性局限于边的长度为正整数的情况。

如果长方形的长和宽都是小数，比如分别为1.2米和0.8米，那么就不易推理出这个长方形面积仍然是长乘宽。因此在教学中，首先需要让学生理解，长为1.2米、宽为0.8米的长方形面积，为什么可以写成乘法算式“1.2×0.8”？

运用放缩变换的方法，首先画出边长为1米的单位正方形ABCD，作为放缩的起点（标准）（见图2）。

图2 单位正方形

而后将AB边扩大1.2倍，也就是1.2米。这时边长为1米的正方形就放大为原来的1.2倍，成为长方形AEFD（见图3）。

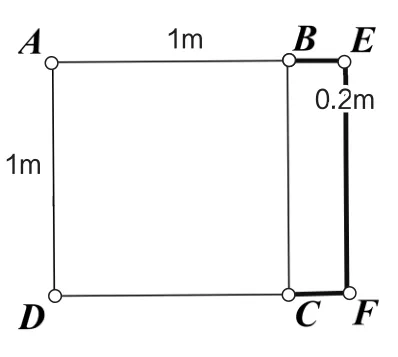
图3 第一次放大示意图

接下来将AD边缩小0.8倍，也就是0.8米。这时图3中长方形AEFD的面积也随之缩小为原来的0.8倍，成为长方形AEHG（见图4）。

图4 第二次缩小示意图

此时，长为1.2米、宽为0.8米的长方形AEHG的面积，就可以写成乘法算式1.2×0.8，这个算式的出现经历了如下的放缩过程。

第一步：确定以边长为1米的单位正方形ABCD作为标准，也就是放缩过程的起点，其面积为

1米 ×1米 =1平方米。

第二步：将单位正方形的面积放大为原来的1.2倍，方法是将正方形ABCD一条边长AB扩大为1.2米。此时长方形面积计算的算式为：

(1.2× 1米 )×1米 =1.2米 × 1米 =1.2平方米

第三步：将长方形AEFD的面积缩小为原来的0.8倍，方法是将图3长方形AEFD的另外一条边长AD缩短为0.8米。这时就得到长为1.2米、宽为0.8米的长方形面积为：

1.2米 ×(0.8×1米 )=1.2米 ×0.8米=0.96平方米

在小学三年级通过“数方格”以及“重复加”所得到的长方形面积公式，并不能直接适用于边的长度为小数或分数的情况。数学课程中的此类问题很多，其本质是关于正整数范围内的规律，如何应用于更广泛范围中的继承性（Permanence）问题。

表1 常见量列表

“继承性”这一说法始见于英国19世纪数学家乔治·皮克科（George Peacock，1791—1858），于1830年在剑桥大学出版社出版的《论代数》①英译：A Treatise on Algebra.前言中，本意是研究算术中的形式如何继承到代数系统中，也就是如何保持算术运算规律和法则适用于代数运算的问题[1]。后来被广泛应用于数学不同领域的类似研究中。

小学低年级对于四则运算的学习，往往局限于对于离散量的直观认识，这些认识往往不能适用于高年级，乃至更高水平的学习。因此运用继承性的思想[2]，让四则运算的认识逐步拓展、提升，体现螺旋上升的课程原理，是数学课程与教学研究的重要课题。

三、小数乘法第一课

小数乘法作为一个单元的学习内容，起始阶段应当让学生熟悉什么情况下会出现两个小数相乘，以及两个小数相乘的放缩过程。为此，可以从思考讨论小数与整数以及小数与小数之间的关系入手。

数是描述客观世界中量（Magnitude）的语言，所谓量指的是范围、大小、多少等方面出现程度变化与差异的对象。比如长短变化带来“长度”，范围大小带来“面积”等等。小学数学课程中常见的量如表1所示。

除了这些体现延展（Extensive）意义的量之外，还有利用以上不同量复合而成，主要描述集中程度（Intensive）的量，比如速度、浓度（密度）、工作效率等。数学课程中关于这些量的内容，既有“概念性（Conceptual）”的意义，也有“背景性（Contextual）”的意义。就是说关于量的知识除了本身作为理解的对象，还可以成为引出其他内容的背景，学习其他内容的工具。小数乘法学习中，充分利用这些内容，将其融入到学习活动中，对于理解小数以及拓展乘法的认识十分有益。

让学生利用熟悉的量，描述数之间的关系，对于体会运算的意义十分有益。比如可以给学生布置如下的任务（Task）：用尽可能多的实例与方法，说明0.5与0.25的关系。学生思考交流的过程中，产生的方法一定是多样的。

方法1：利用加法运算。因为0.25＋0.25＝0.5，所以0.5是0.25的2倍，或者0.25是0.5的二分之一。

方法2：利用长度（数轴）。在数轴上标记0.25和0.5，可以发现0.5是1的二分之一，0.25是1的四分之一，因此0.5是0.25的2倍（见图5）。

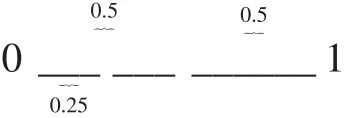
图5 数轴示意图

方法3：利用人民币。因为0.5元是5角（或50分），0.25元是2角5分（或25分），所以0.5是0.25的2倍。

方法4：利用时间。0.5小时等于30分钟，0.25小时等于一刻钟，也就是15分钟。30分钟是15分钟的2倍，所以0.5是0.25的2倍。

凡此都是利用学生已经熟悉的量的放缩过程，引出算式0.25×2=0.5。至此对于算式的理解就不局限于“2个0.25相加”，还包括放缩变换的意义。比如，0.25放大4倍等于1，0.5放大2倍等于1，所以0.25放大2倍是0.5。再比如，长度为1的线段缩短一半是0.5，再缩短一半就是0.25。所以0.5缩短一半是0.25。由此还能够引出算式0.5×0.5=0.25。

在此基础上，可以进一步引导学生思考算式0.25×0.2的含义。比如可以给学生布置任务：用尽可能多的实例说明算式0.25×0.2的含义。

学生首先可能想到的是前面算式0.25×2与0.25×0.2的关系，因为0.2是2缩小10倍的结果，所以0.25×0.2的结果应当是0.5缩小10倍，也就是0.05。

还可以用学生已经熟悉的长度进行解释，如果把因数0.2视为0.2米，也就是20厘米。根据前面的经验，20厘米乘0.25就是将20厘米缩短一半的一半，第一次缩短一半等于10厘米，第二次缩短一半是5厘米，5厘米等于0.05米。

学生学习计算，学习目标不能局限于“怎么算”，至少还应当包括“何时这样算”和“为何这样算”。如今的课堂教学倡导“学习活动为核心（Learning Centered）”，这就要求教学过程和方法的改变，从“教师教的活动为主”转变到“学生学的活动为主”。实现这种转变首先需要研究的问题是如何设计学习活动？学生的学习活动是通过教师布置的学习任务而开展的，学习任务是依据学习目标而设计的。因此，教学研究的着力点首先应当放在“学什么”的问题上。