考虑m弱化效应的水平循环受荷桩分析
魏丽敏,张超凡,翟顺,何群,李宏泉
考虑弱化效应的水平循环受荷桩分析
魏丽敏,张超凡,翟顺,何群,李宏泉
(中南大学 土木工程学院,湖南 长沙,410075)
现行规范采用法分析水平受荷桩的内力和变位时,将地基系数的比例系数视为定值。承受水平循环荷载作用的桩,当桩周土体发生较大位移时,其随桩在地面处位移增大和加载次数增加均呈减小趋势。基于现场原型试验结果,分别建立随桩在地面处位移0及循环加载次数的幂函数关系式;考虑的上述弱化效应,构建水平循环受荷桩桩身挠曲微分方程,编制其内力与变位有限差分求解程序,通过与现场试验对比分析,验证该计算方法能较好地适用于深厚软土地区在地面处水平位移大于4 mm的水平循环受荷桩的内力与变位计算。
水平受荷桩;循环荷载;弱化;有限差分法;现场原型试验
国内外许多研究者对水平受荷桩的内力与变位进行了系统研究[1−4]。目前,常用的理论分析方法有法、法、法和−曲线法等。国内设计规范普遍采用的法假定地基土处于弹性状态,地基系数随深度呈线性变化,其比例系数是与土层特性相关的常量。而在实际工程中,当土体位移较大时,土体处于弹塑性状态,其不再是常量,随桩在地面处位移呈非线性变化[5]。王梅等[6]将与位移建立幂函数关系,引入单桩法分析中,以考虑的非线性影响;吴峰 等[7]基于大量桩基水平静荷载试验,建立与桩在地面处位移的相互关系式,用于推算土体大位移下的。计算结果表明,考虑随桩在地面处位移的非线性变化,能够提高计算结果的精度。桩基除承受一般静荷载外,有时还要受循环荷载的影响,如铁路桥梁桩基受列车动荷载、海岸高桩基础受风浪荷载等,会引发土体力学强度与刚度出现循环弱化效应[8−9]。POULOS等[10−13]结合桩基循环荷载试验,采用曲线法研究了桩基力学响应规律。俞剑等[14]结合水平循环荷载下海上风电桩基模型试验,在对现有曲线改进的基础上提出了大周数水平循环荷载下单桩计算方法。胡安峰等[15]通过对ABAQUS二次开发实现土体刚度衰减模拟,进而研究长期风浪荷载下桩基础的累计侧向位移问题。王其标等[16]采用流函数波浪理论,将Morison方程和曲线结合以分析桩基础内力与变形。然而,受限于现场测试技术、试验成本等因素,实测曲线通常难以获得;而采用规范曲线(如美国API规范)计算结果又与实际工程结果有所差别[17−18],这些无疑制约了曲线法的推广应用。与此同时,在常规法应用中,考虑循环荷载引起土体强度与刚度弱化而导致逐渐减小的研究很少,忽略的循环弱化效应对实际工程存在安全隐患,有必要对此进行深入研究。为此,本文作者基于钻孔灌注桩水平荷载试验,考虑土体发生大位移情况下的非线性及其循环弱化效应,确定与桩在地面处位移0、循环次数的函数关系,建立相应的桩身挠曲微分方程;采用有限差分法进行求解并编制相应程序,结合现场试验验证计算方法的准确性。
1 现场试验与m弱化效应
1.1 试验概况
钻孔灌注桩水平荷载试验采用双桩对推的加载方式,场地位于浙江省宁波市,桩径为1.00 m,桩长为45.00 m,桩帽长×宽×高为1.80 m×1.40 m×1.00 m,采用C40混凝土浇筑。图1所示为试验装置的正面示意图。桩在地面处水平位移采用百分表测量,在桩帽底以上10.00,60.00和95.00 cm高度处对称于水平力作用面分别安装2只百分表,间距为1.00 m。桩身应变采用对称布置于钢筋笼上的钢筋计量测,在地面下34.00 m的深度范围内,按照上密下疏的原则,共设置10个测试断面。为保证试验精度,基准桩布置在试桩侧面,距试桩净距为3.50 m,如图2所示。
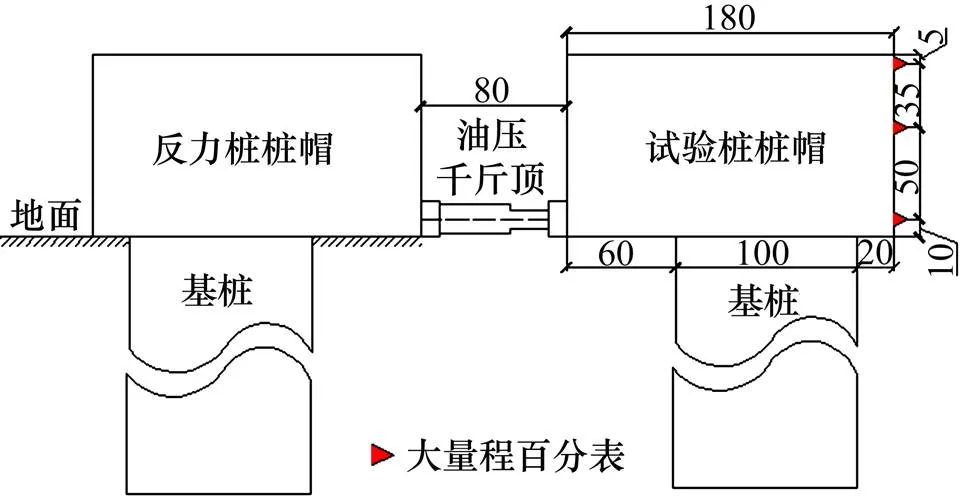
数据单位:cm。
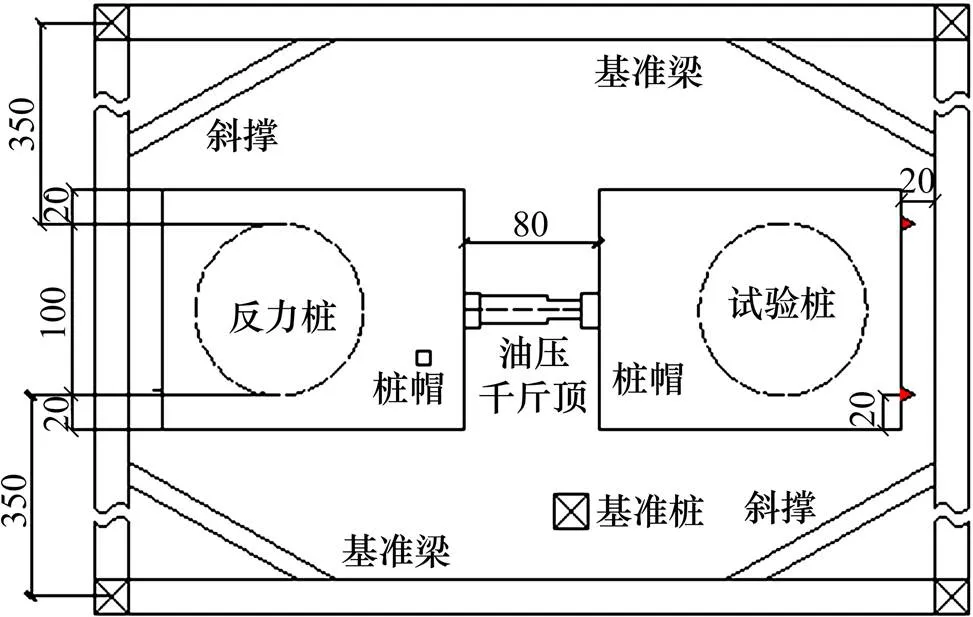
数据单位:cm。
本次试验分别采用单向循环加卸载法和慢速维持荷载法进行。依据相关规范[19−20],单向循环加卸载法以40 kN为初始水平荷载,以20 kN为增量逐步增大,当桩顶位移达到6.00 mm时,终止加载;卸载完成并静止72 h后,进行慢速维持荷载法试验,以100 kN为初始荷载,根据桩顶位移变化及桩基条件以25 kN为增量逐步增大,加载至桩基被破坏为止。
试验场地土层自上而下分布为:0~4.80 m为杂填土,结构松散,均匀性差;4.80~13.10 m为流塑状淤泥,具有高孔隙比、高压缩性;13.10~17.90 m为软塑状粉质黏土,局部粉粒质量分数高,具有中—高压缩性;17.90~30.50 m范围内为流—软塑淤泥质粉质黏土,具有高压缩性;30.50 m以下为软塑粉质黏土,具有中等压缩性。
1.2 桩在地面处的位移
根据单向循环加卸载法试验结果,绘制试验桩在地面处位移−时间−荷载曲线,如图3所示;每级荷载第5次循环加载时桩在地面处位移随荷载变化曲线,如图4所示。
从图3和图4可见桩在地面处位移变化分2个 阶段。
1) 弹性阶段(桩在地面处位移0≤4.00 mm)。随着荷载以20 kN为增量增加,桩在地面处位移基本呈线性增大趋势,每级增量大致为0.60 mm;该阶段桩在经受任一级水平荷载反复作用时,桩在地面处位移大致相同且变形大部分可以恢复,16%~19%不能恢复,桩周土近似处于弹性阶段。
2) 弹塑性阶段(0>4.00 mm)。当荷载由140 kN增至160 kN时,桩在地面处位移增量为2.80 mm,明显大于线弹性阶段位移增量(0.60 mm)。桩在地面处位移急剧增大为6.64 mm,说明此时土体已经进入弹塑性状态。可以认为:当深厚软土地区桩在地面处位移小于4.00 mm时,桩周土可视为弹性状态,按常规法进行计算;当桩在地面处位移大于4.00 mm时,桩周土体进入弹塑性状态,采用法计算时需考虑随桩在地面处位移变化的非线性。
1.3 m的非线性变化与循环弱化效应
1.3.1 常规法
传统法基于竖向弹性地基梁模型,将桩周土体离散为相互独立的水平弹簧,假定地基抗力系数沿深度线性分布,桩身挠曲微分方程如下:
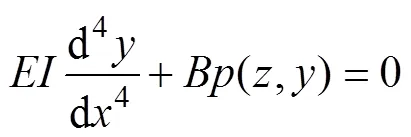
其中:

()为地面以下深度处桩侧土抗力;为桩身水平位移;为基桩刚度;为桩身宽度。上述方法适用于土体发生小位移0(0cr,cr为土体弹性、弹塑性界限时桩在地面处位移)的情况,此时,桩周土处于弹性状态,为常量,应采用试验实测值,无实测资料时可参考相关规范取值[21]。
1.3.2随桩在地面处位移的非线性变化
单向循环加卸载法与慢速维持荷载法试验成果均可用于研究随桩在地面处位移的变化规律。为节约试验成本,本次单向循环加卸载试验终止较早(桩顶位移<6.00 mm)。为分析土体的全过程变化规律,以慢速维持荷载法试验结果为例进行说明。
“建筑基桩检测技术规范”[19]规定:当桩顶自由且水平力作用位置位于地面处时,应按

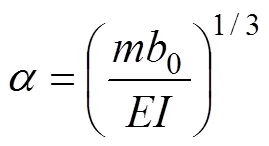

由式(3)和(4)计算各级荷载下地基系数的比例系数,并绘制随桩在地面处位移0的变化曲线,见图5。由图5可知:随桩在地面处位移0的增大而衰减,且衰减速率越来越慢,符合规范[21]的规定,即当土体发生较大位移时(0>cr),其应适当降低。
将图5试验结果采用幂函数

进行拟合(其中,a和k为拟合参数),可得a =10.763,k =−0.84,相关系数R=0.98。这说明土体位移较大时,m随在地面处位移y0增加呈幂函数衰减趋势。
当无试验资料时,式(5)中的非线性参数和可按以下方法确定:基于现场试验,软黏土的可取−0.70~−0.85,土体越软,对应的越小[21];被确定后,由0=6.00 mm查找相关规范[15]获取对应的,由式(5)反算[22]。
1.3.3随循环次数的弱化
循环荷载作用下桩周土体会产生弱化效应,对应的会逐渐降低。依据单向循环加卸载试验所得桩顶位移及式(3)和(4)所得第次加载时土体,绘制不同荷载等级下随水平荷载循环次数变化的曲线,如图6所示。
由图6可知:在同一荷载等级下,水平地基系数的比例系数随循环次数的增加呈幂函数衰减。
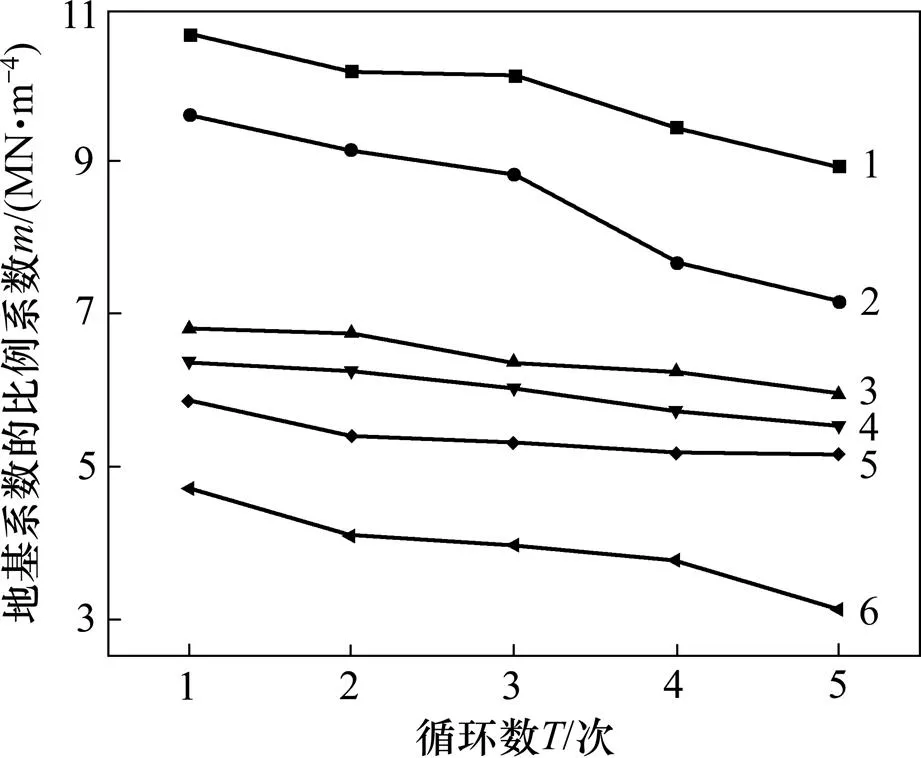
水平荷载H/kN:1—60;2—80;3—100;4—120;5—140;6—160。
据此可得出与加载次数之间的衰减因子E为

式中:c和s分别为每级荷载下第次循环加载和第1次加载的地基系数的比例系数;为循环弱化因子。依据模型(6)对图6中数据进行拟合,结果如表1所示。
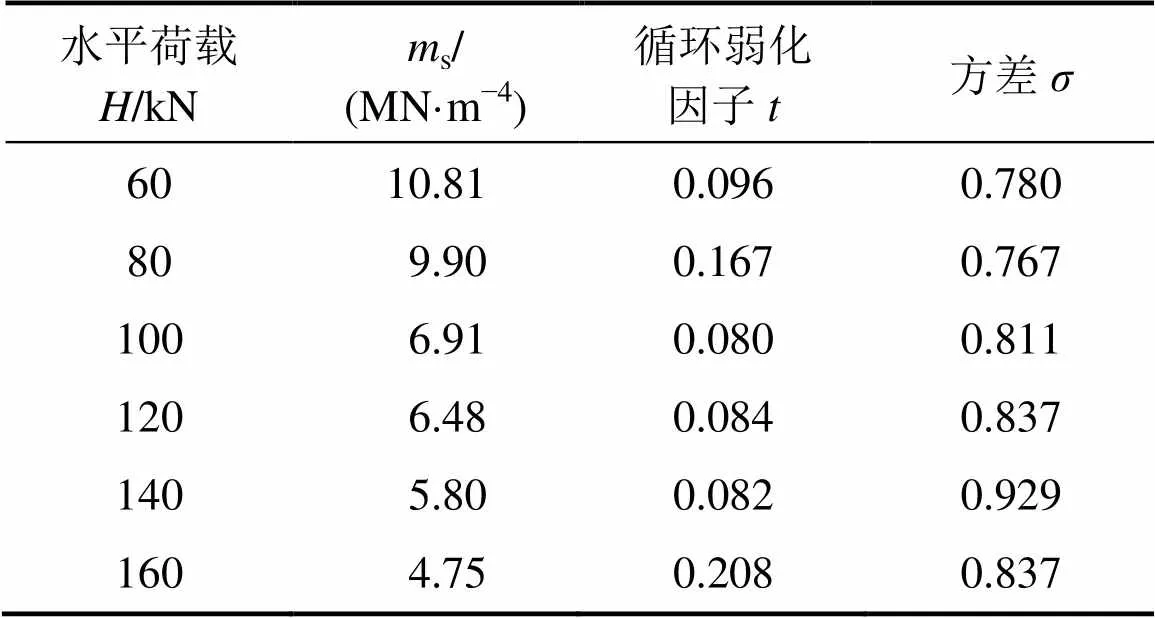
表1 循环弱化因子拟合
由表1可知:当荷载为60~140 kN,桩周土近似处于弹性阶段时,循环弱化因子基本处于0.080~0.096之间,可忽略其的循环弱化效应;当荷载达到160 kN,桩周土进入弹塑性状态时,增大至0.2左右。无试验数据时,可依据土体性质取值,为0~0.3[10]。
2 水平循环受荷桩内力与变位分析
2.1 桩身挠曲差分方程建立
对工程桩,除水平荷载外,桩顶往往还承受竖向荷载和弯矩作用,如图7所示。

图7 有限差分法计算模型示意图
假设桩身为弹性,桩身抗弯刚度为,桩顶力为常数,则考虑非线性及循环弱化效应的桩身挠曲微分方程如下:

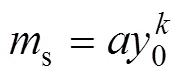
如图7所示,为使用差分法求解方程,设桩全长为,将其等分成段,每段长度为。为避免编程时出现零下标和负下标,将桩顶节点编为3号,桩尖节点则为+3,且两端分别延长并设虚拟节点1,2和+4,+5,对于第个节点,有以下关系:
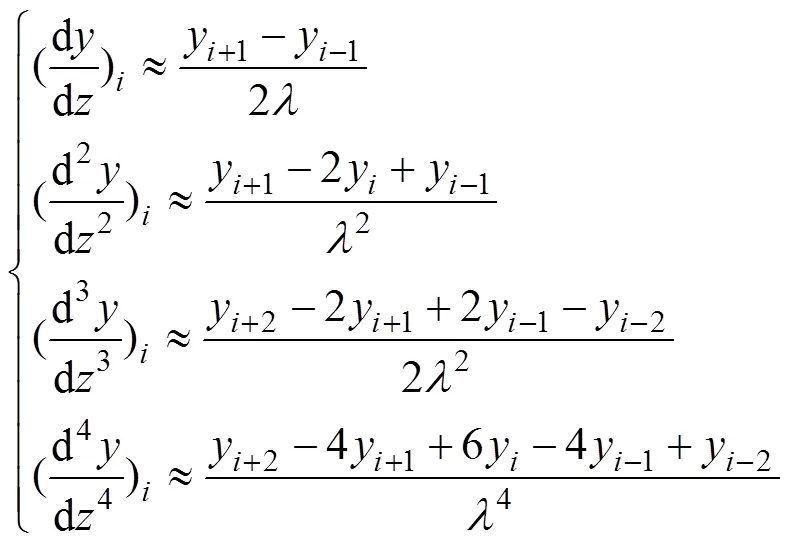
将式(8)代入式(7),可得桩身挠曲差分方程:
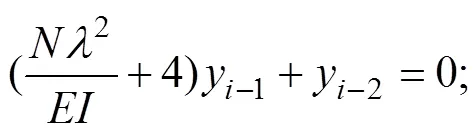
将桩在地面处荷载0、0作为边界条件,则有
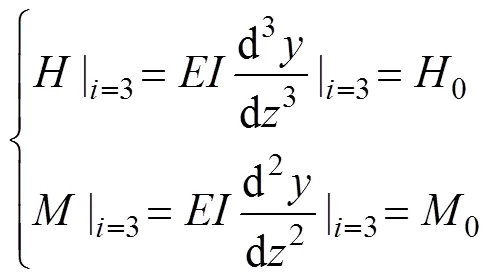
对非嵌岩弹性桩,可忽略桩底水平力与弯矩,则桩底边界条件为
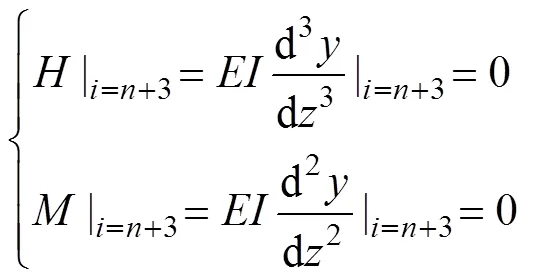
2.2 方程求解与程序编制
根据式(8)和(9),结合边界条件式(10)和(11),采用追赶法解得各节点处桩身挠度y,代入式(8)可得各节点处桩身弯矩为
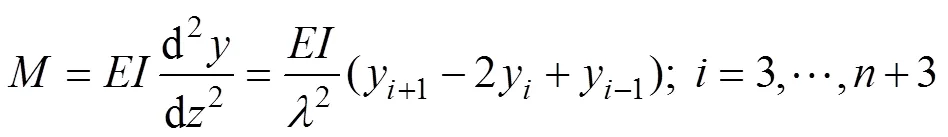
桩侧土抗力为

为便于求解,将上述过程采用FORTRAN语言编程,程序流程如图8所示。
3 单桩试验结果与理论计算结果对比
3.1 桩身挠度
按照文献[23]中方法,根据桩身布设的钢筋计测得的应变获得每级荷载第5次循环加载时桩身挠曲线、桩在地面处位移随加载次数的变化规律,将其与按前述理论计算所得结果进行对比,如图9和图10所示。
由图9可见:计算与实测获得的桩身挠度变化趋势基本一致,沿深度均呈递减趋势,在地面处最大,主要分布在地面以下10.00 m深度范围内。
由图10可见:当桩在地面处位移小于4.00 mm时,位移随加载次数增加基本不变,即不存在循环弱化;当桩在地面处位移大于4.0 mm时,桩周土进入弹塑性状态;随着加载次数增加,桩在地面处位移由4.90 mm增大至6.64 mm,且增量由第1次加载时的1.10 mm减小到第5次加载时的0.30 mm,这主要是由于循环荷载造成桩周土体刚度下降,由此使土体产生循环弱化效应;在同级荷载作用下位移计算值与实测桩在地面处位移差值介于0.01~0.47 mm,验证了计算方法的正确性。

1—60 kN时的实测值;2—60 kN时的计算值;3—100 kN时的实测值;4—100 kN时的计算值;5—140 kN时的实测值;6—140 kN时的计算值;7—160 kN时的实测值;8—160 kN时的计算值。

1—60 kN时的实测值;2—60 kN时的计算值;3—100 kN时的实测值;4—100 kN时的计算值;5—140 kN时的实测值;6—140 kN时的计算值;7—160 kN时的实测值;8—160 kN时的计算值。
3.2 桩身弯矩
每级荷载第5次循环加载时桩身弯矩计算值与实测值对比分别如图11和图12所示。

1—60 kN时的实测值;2—60 kN时的计算值;3—100 kN时的实测值;4—100 kN时的计算值;5—140 kN时的实测值;6—140 kN时的计算值;7—160 kN时的实测值;8—160 kN时的计算值。
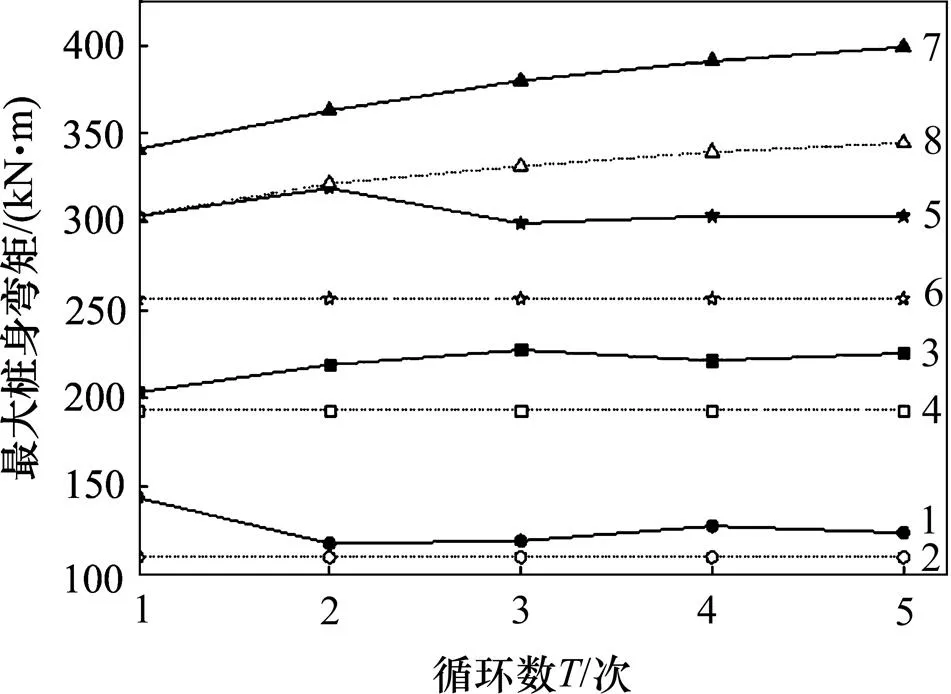
1—60 kN时的实测值;2—60 kN时的计算值;3—100 kN时的实测值;4—100 kN时的计算值;5—140 kN时的实测值;6—140 kN时的计算值;7—160 kN时的实测值;8—160 kN时的计算值。
从图11可见:桩身弯矩计算值与实测值变化趋势基本一致,沿深度均先增加后急剧减小,在地面下0~10 m范围内弯矩较明显,最大弯矩约在地面下 3.50 m处。
从图12可见:当水平荷载小于140 kN时,桩身最大弯矩随加载次数变化不大;当荷载达到160 kN后,随着加载次数增多,最大弯矩逐渐增大;在同级荷载下,最大弯矩的计算值与实测值的差值介于20~50 kN··m,相对误差为11%~14%,验证了计算方法的正确性。
4 结论
1) 当桩在地面处位移0大于cr时,桩身挠度和弯矩随着荷载增大而急剧增大,随加载次数的增加而增大,揭示了大位移情况下地基系数的比例系数存在弱化效应。
2) 建立了大位移情况下随桩在地面处位移0增大而衰减的幂函数关系,建立了随循环加载次数变化的幂函数关系。
3) 考虑随地面处位移变化的非线性及循环弱化效应,建立了基桩挠曲微分方程,编制了桩身内力与变位的有限差分法求解程序。现场试验结果验证了该计算方法的正确性。
[1] 苏静波, 邵国建, 刘宁. 基于曲线法的水平受荷桩非线性有限元分析[J]. 岩土力学, 2006, 27(10): 1781−1785. SU Jingbo, SHAO Guojian, LIU Ning. Nonlinear finite element analysis of piles under lateral load based oncurves[J]. Rock and Soil Mechanics, 2006, 27(10): 1781−1785.
[2] 张玲, 赵明华, 赵衡. 双层地基水平受荷桩受力变形分析[J]. 岩土力学, 2011, 32(S2): 302−305. ZHANG Ling, ZHAO Minghua, ZHAO Heng. Analysis of a laterally loaded pile in a two-layer soil[J]. Rock and Soil Mechanics, 2011, 32(S2): 302−305.
[3] 常林越, 王金昌, 朱向荣, 等. 双层弹塑性地基水平受荷桩解析计算[J]. 岩土工程学报, 2011, 33(3): 433−440. CHANG Linyue, WANG Jinchang, ZHU Xiangrong, et al. Analytical calculation of laterally loaded piles in double-layered elastoplastic soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 433−440.
[4] 卓杨, 刘兹胜, 吴锋, 等. 水平受荷桩桩−土作用的有限元分析[J]. 地下空间与工程学报, 2009, 5(S2): 1554−1556, 1561. ZHUO Yang, LIU Zisheng, WU Feng, et al. Finite element analysis on pile−soil interaction of pile under horizontal load[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(S2): 1554−1556, 1561.
[5] 李建光, 马培贤, 刘春来. 地基土水平抗力系数的比例系数与桩顶水平位移相互关系研究[J]. 地基处理, 2007, 18(3): 3−7. LI Jianguang, MA Peixian, LIU Chunlai. A study on correlation of proportionality factor of coefficient of subgrade horizontal reaction and pile heads horizontaldisplacement[J]. Ground Improvement, 2007, 18(3): 3−7.
[6] 王梅, 楼志刚, 李建乡, 等. 水平荷载作用下单桩非线性法试验研究[J]. 岩土力学, 2002, 23(1): 23−26. WANG Mei, LOU Zhigang, LI Jianxiang, et al. Nonlinear analysis ofmethod for single pile under lateral loading[J]. Rock and Soil Mechanics, 2002, 23(1): 23−26.
[7] 吴锋, 时蓓玲, 卓杨. 水平受荷桩非线性法研究[J]. 岩土工程学报, 2009, 31(9): 1398−1401. WU Feng, SHI Beiling, ZHUO Yang. Nonlinearmethod for piles under lateral load[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1398−1401.
[8] ANDERSEN K H, ROSENBRAND W F, BROWN S F, et al. Cyclic and static laboratory tests on Drammen clay[J]. Journal of the Geotechnical Engineering Division, 1980, 106(5): 499−529.
[9] VUCETIC M, DOBRY R. Degradation of marine clays under cyclic loading[J]. Journal of Geotechnical Engineering, 1988, 114(2): 133−149.
[10] POULOS H G. Single pile response to cyclic lateral load[J]. Journal of the Geotechnical Engineering Division, 1982, 108(3): 355−375.
[11] ROSQUOET F, THOREL L, GARNIER J, et al. Lateral cyclic loading of sand-installed piles[J]. Soils and Foundations, 2007, 47(5): 821−832.
[12] 朱斌, 杨永垚, 余振刚, 等. 海洋高桩基础水平单调及循环加载现场试验[J]. 岩土工程学报, 2012, 34(6): 1028−1037. ZHU Bin, YANG Yongyao, YU Zhengang, et al. Field tests on lateral monotonic and cyclic loadings of offshore elevated piles[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1028−1037.
[13] 陈仁朋, 顾明, 孔令刚, 等. 水平循环荷载下高桩基础受力性状模型试验研究[J]. 岩土工程学报, 2012, 34(11): 1990−1996. CHEN Renpeng, GU Ming, KONG Linggang, et al. Large-scale model tests on high-rise platform pile groups under cyclic lateral loads[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 1990−1996.
[14] 俞剑, 黄茂松, 张陈蓉. 黏土中两种不同直径单桩水平循环加载模型试验与分析[J]. 岩土力学, 2016, 37(4): 973−980. YU Jian, HUANG Maosong, ZHANG Chenrong. Model tests and analysis of single piles with two different diameters subjected to cyclic lateral loadings in clay[J]. Rock and Soil Mechanics, 2016, 37(4): 973−980.
[15] 胡安峰, 张光建, 贾玉帅, 等. 刚度衰减模型在大直径桩累积侧向位移分析中的应用[J]. 浙江大学学报(工学版), 2014, 48(4): 721−726. HU Anfeng, ZHANG Guangjian, JIA Yushuai, et al. Application of degradation stiffness model in analysis of cumulative lateral displacement of monopile foundation[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(4): 721−726.
[16] 王其标, 杨敏, 靳军伟. 基于流函数理论的近海风机桩基础受力性能比较分析[J]. 岩土工程学报, 2013, 35(S2): 1122−1125. WANG Qibiao, YANG Min, JIN Junwei. Mechanical properties of pile foundation of offshore wind turbines based on stream function wave theory[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 1122−1125.
[17] 李雨润, 袁晓铭, 李帆. 基于API规范的液化土层桩基曲线修正计算公式[J]. 地震工程与工程振动, 2010, 30(6): 148−153. LI Yurun, YUAN Xiaoming, LI Fan. Modified formula for calculatingcurves of pile foundation in liquefied soil layer based on API code[J]. Earthquake Engineering and Engineering Dynamics, 2010, 30(6): 148−153.
[18] 李炜, 陈法波, 吕娜, 等.曲线法在海上风电基础桩土作用计算中的适用性研究[J]. 水力发电, 2011, 37(10): 96−99.LI Wei, CHEN Fabo, LÜ Na, et al. Suitability ofcurve on pile-soil interaction analysis for offshore wind turbine[J]. Water Power, 2011, 37(10): 96−99.
[19] JGJ 106—2014, 建筑基桩检测技术规范[S].JGJ 106—2014, Technical code for testing of building foundation piles [S].
[20] JGJ 94—2008, 建筑桩基技术规范[S]. JGJ 94—2008, Technical code for building pile foundations[S].
[21] TB 10093—2017, 铁路桥涵地基和基础设计规范[S]. TB 10093—2017, Code for design on subsoil and foundation of railway bridge and culvert[S].
[22] 翟顺. 深厚软土地区水平循环受荷桩工作特性研究[D]. 长沙: 中南大学土木工程学院, 2017: 41−56. ZHAI Shun. Single pile response to cyclic lateral load in deep soft soil area[D]. Changsha: Central South University. School of Civil Engineering, 2017: 41−56.
[23] 夏启迪. 邻近开挖对深厚软土桩基内力与变形影响现场试验研究[D]. 长沙: 中南大学土木工程学院, 2014: 20−25. XIA Qidi. Study on pile foundation adjacent to excavation in deep-soft soil area[D]. Changsha: Central South University. School of Civil Engineering, 2014: 20−25.
(编辑 陈灿华)
Analysis of lateral cyclic loaded pile considering weakening effect ofvalue
WEI Limin, ZHANG Chaofan, ZHAI Shun, HE Qun, LI Hongquan
(School of Civil Engineering, Central South University, Changsha 410075, China)
The ratio coefficientof the ground coefficient was considered as a constant, whenmethod was used to analyze the internal force and displacement of lateral loaded pile in current specifications.of the soil around the lateral cyclic loaded pile decreases with the increase of the displacement of pile top and the loading cycles times. Two power function relationships were established separately based on the field prototype test results. One was thatdecreased with the increase of the displacement of pile top, and the other was thatdecreased with the increase of the loading cycles numbers. Based on the weakening effect of, the differential equation of pile deflection of lateral cyclic loaded pile was established, and then the finite difference program to calculate internal force and displacement was compiled. After comparing the field test results with those from calculation, it is proved that the proposed method is proved can be applied well in the calculation of lateral cyclic loaded pile, of which the horizontal displacement at the ground surface is larger than 4 mm in deep soft soil area.
laterally loaded pile; cyclic loading; weakening effect of; finite difference method; field prototype test
10.11817/j.issn.1672-7207.2018.09.021
TU447
A
1672−7207(2018)09−2272−08
2017−10−12;
2017−12−27
上海铁路局科研计划项目(2013144);国家自然科学基金资助项目(51478478) (Project(2013144) supported by Scientific Research Program of Shanghai Railway Bureau; Project(51478478) supported by the National Natural Science Foundation of China)
魏丽敏,博士,教授,博士生导师,从事岩土工程研究;E-mail: lmwei99@163.com

