四足变胞爬行机器人步态规划与运动特性

赵欣，康熙，戴建生, 2



四足变胞爬行机器人步态规划与运动特性

赵欣1，康熙1，戴建生1, 2

(1. 天津大学 现代机构学与机器人学国际中心，天津，300350；2. 国王学院 机械工程系，英国 伦敦，WC2R 2LS)

为解决绝大多数足式机器人的腰部是固定不可变的问题，研究一种腰部可变的四足爬行机器人，并分析腰部和腿部的形态，从数学上给出腰部构态变换的条件。另外，考虑腰部可变设计出扭腰直行步态和扭腰原地旋转步态，并将其与传统步态进行比较，分析不同步态在稳定裕度、活动空间和通过狭窄弯道等方面不同的优势。最后，研究腰部变胞使机器人在足尖活动空间、视觉观察等方面具有的特征，显示所设计的机器人对环境的适应能力。研究结果表明：可基于变胞机构设计爬行机器人腰部使其构态可变，腰部构态可变可以提高四足机器人的灵活性和环境适应能力。

四足变胞爬行机器人；腰部构态；步态规划；运动特性

近几年，四足机器人由于机构简单、运动灵活以及方便控制等特点，在抢险救灾、探险等方面具有广阔的应用前景[1]，是机器人领域的研究重点。在此背景下，国内外许多学者研究开发了多种四足机器人。例如较为著名的TITAN[2]系列机器人、LittleDog[3]以及BigDog[4]，这些机器人实现了较复杂的控制，能够完成一定的任务。随着机器人技术的不断进步，机器人面临的任务更加复杂多变，工作环境更加复杂，这不仅要求机器人具有更智能的控制水平，而且对机器人骨架−机构提出了更高的要求，因此，一些腰部可动的机器人也相继被研发。LEWIS[5]设计了机器人GEO，其腰部安装4个电机，使腰部可以实现俯仰、扭动和平面旋转动作；PARK等[6]设计了一种腰部具有1个旋转关节的四足机器人，研究证明了具有腰部关节的机器人在行走时具有更好的稳定性，并且可以通过狭窄的弯曲轨道。DAI等[7−8]创造性地提出了变胞灵巧手，将变胞原理应用于手掌结构之中，使之可以作变胞运动，极大地提高了机械手的操作度和灵巧度。而爬行机器人是机械手的倒置[9]，将变胞机构应用于机器人的腰部，就得到了腰部可变的变胞爬行机器人。相比以往腰部固态的爬行机器人只能靠腿部形状的改变来实现特定的动作而言，腰部可变的爬行机器人可通过腰部变形实现不同的步态，以适应不同的应用环境要求，同时增强了机器人本身的稳定性和稳定裕 度[10]。基于变胞原理以及MÜLLER[11]提出的平面四杆奇异构型，提出一种四足变胞爬行机器人，其腰部只有1个舵机，仅依靠1个驱动控制腰部完成构态变化，从而实现变胞过程。针对提出的新型四足变胞爬行机器人，本文介绍其机构设计以及腰部结构；说明机器人腰部构态变化，明确腰部变胞条件；提出2种扭腰步态，并与传统步态进行对比，分析新型步态和传统步态的不同特征；对机器人腿部活动空间、实际应用进行分析。

1 四足变胞爬行机器人机构设计

从MÜLLER[11]提出的平面四杆奇异构型出发，改变平面四杆机构每个杆件的形状，使其成为机器人的腰部，由此得到的四足变胞爬行机器人样机和简化模型分别如图1和图2所示。

图1 四足变胞爬行机器人样机

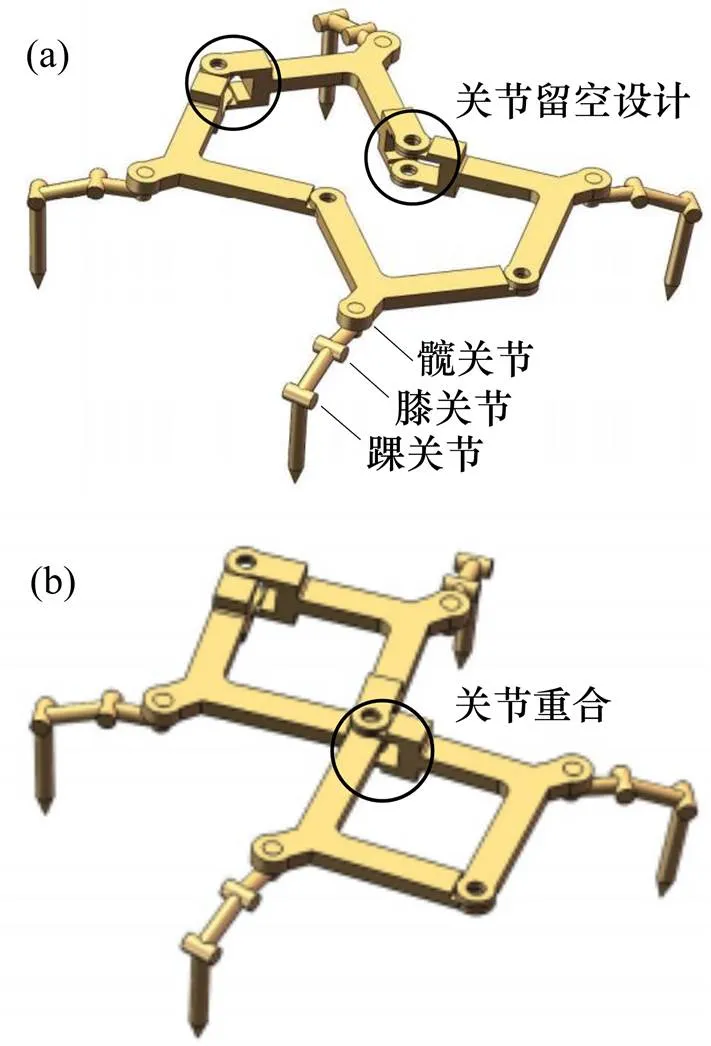
(a) 腰部关节设计；(b) 腰部关节重合

由图1和图2可见：机器人腰部为平面四杆机构，每个杆件设计为尺寸相等、形状一致的直角杆件；腰部有4个旋转关节，其轴线均垂直于腰部平面；机器人腿部采用昆虫型设计，由3个旋转关节组成，分别定义为髋关节、膝关节、踝关节，髋关节与腰部直角杆件弯折处相连，其轴线在腿部平面内并垂直于腰部所在平面，膝关节、踝关节轴线垂直于腿部平面；3个关节将腿部分为大腿、中间腿、小腿3部分。

在腰部关节设计上，将2个相邻的关节中间部分留空，保证其留空的距离可以使与之相对的关节进入这个空隙，如图2(a)所示；关节中间留空的设计，使腰部关节在旋转的过程中，相对2个关节的轴线可以重合，如图2(b)所示。同时，在留空关节右侧增加挡板，保证关节轴线能够完美重合。

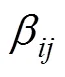
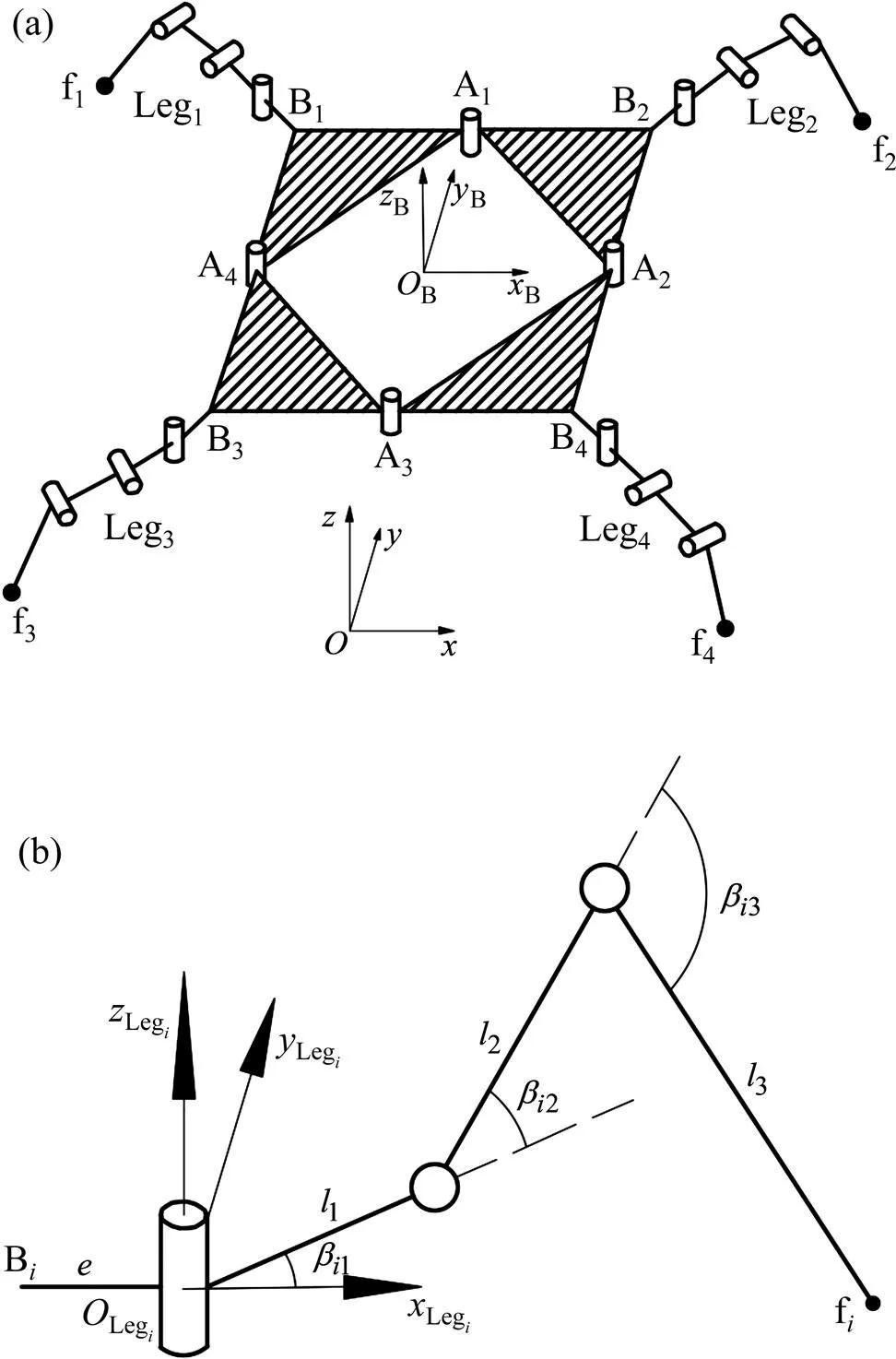
(a) 机器人机构简图；(b) 腿部机构简图

机器人各机构尺寸设定如表1所示。

表1 机器人几何尺寸

为方便简明地表示机器人的腰部形态，以下适当简化机器人腰部的形态图，用“○”表示各旋转关节，用三角形表示直角杆件，其杆件数及旋转关节数仍 为4。

在之后的机器人分析中，为使表述更简化、精确，进行以下假设。

假设1：机器人位于平坦地面，且腰部平面始终与地面平行。机器人移动或变形过程中，腰部平面与地面平行，方便进行稳定性分析。

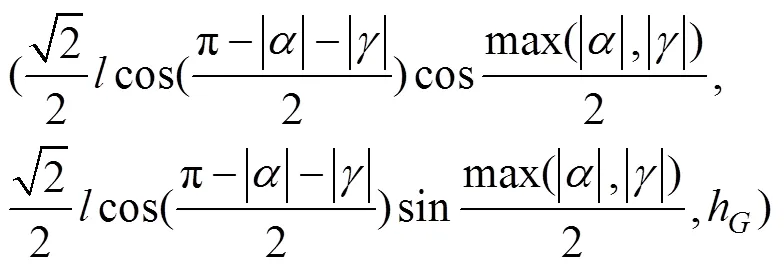
式中：h为重心在轴的坐标，与身体高度以及腿的位置形态有关。

(a) 机器人初始位姿；(b) 机器人腰部重合时初始位姿；(c) 机器人腰部扭动时位姿

图4 机器人重心位置假设

Fig. 4 Hypothesis of gravity center of robot

2 腰部构态变换

直角杆件和关节留空的设计使四足变胞爬行机器人在行走的过程中，可根据环境需要改变腰部构态，接下来明确腰部构态的变化规律和条件。

由于平面四杆机构以及2杆机构只有1个自由度，因此，要实现腰部构态的变化，只需在1个旋转关节处安装驱动装置。选定A2为主动关节，A1，A3和A4为被动关节。因此，在腰部变化过程中，腰部构态便由A2处的关节角度确定。

随着A2处内角变化，腰部构态会逐渐发生变化，各腰部构态如图6所示。腰部构态与A2处内角的对应关系如表2所示。由于只在关节A2处安装驱动，因此，图5(d)所示关节A1和A3轴线重合后并不能作为二杆机构进行研究。综上，本文只针对图6(a)()以及图6(c)()进行研究。

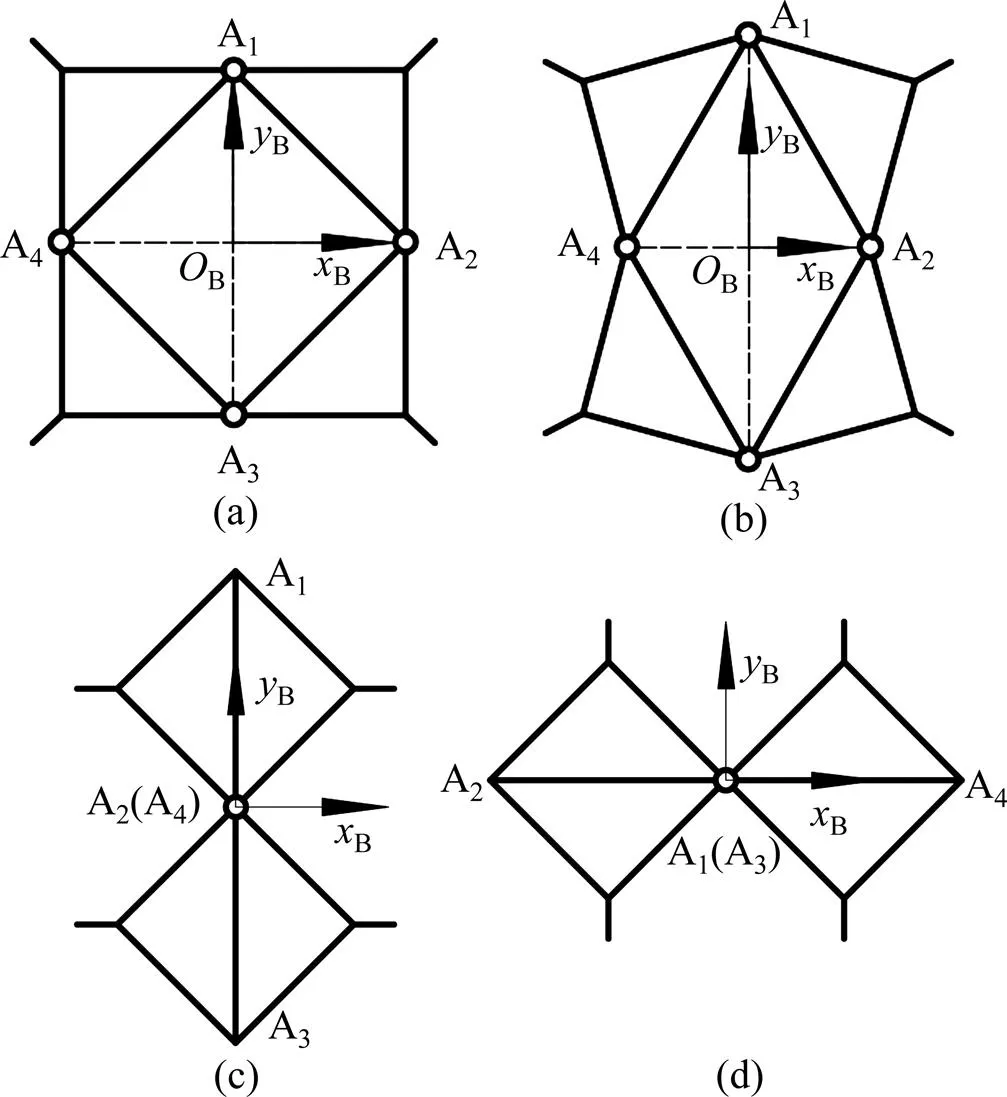
(a) 正方形构态；(b) 过渡构态；(c) 关节轴线重合构态；(d) 关节轴线重合构态

表2 θ2与腰部构态的关系

当腰部A2和A4关节轴线重合腰部变为二杆机构，重合的关节轴线变为二杆机构的转动副。现说明腰部为2杆机构时，腰部扭动的条件。

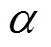
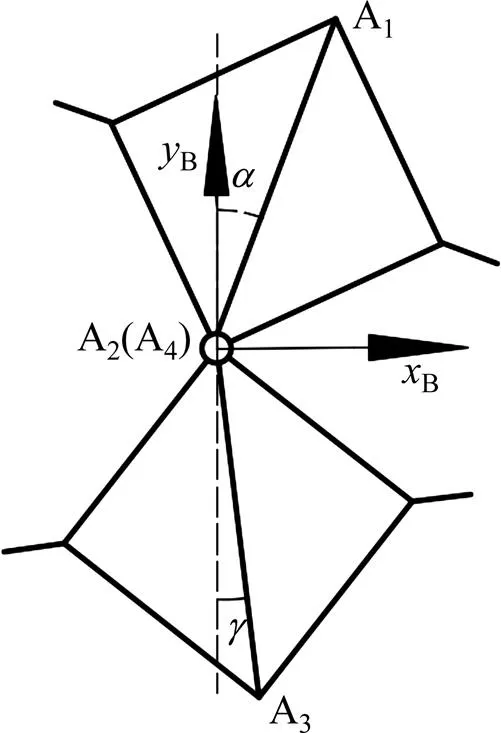
图7 腰部绕重合关节转动

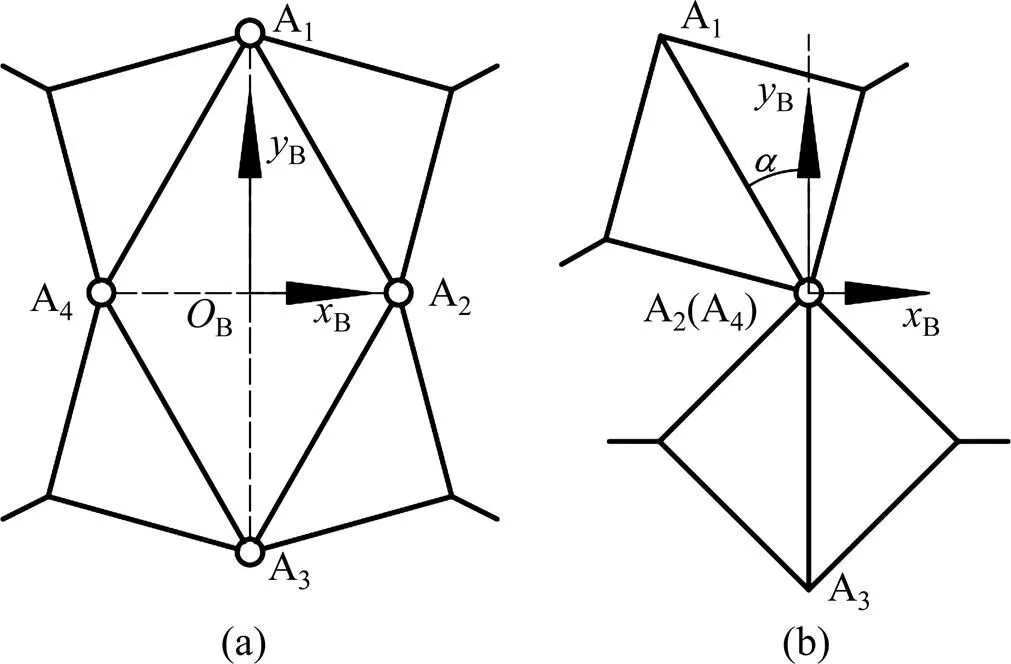
(a) 过渡构态；(b) 关节轴线重合构态

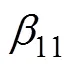
图9 腰部扭转最大角度说明

通过上述说明，明确了四足变胞机器人腰构态以及构态变换条件以及腰部扭转角度，接下来便分析这种变胞结构在机器人腰部的应用以及使机器人具有的运动特性。

3 四足变胞爬行机器人步态规划

针对四足爬行机器人的步态规划已有较多的研究成果[12−14]，在此基础上，利用本文所介绍的机器人腰部可变的特征，提出扭腰直行步态和扭腰原地旋转步态，并与传统步态进行比较，分析不同步态具有的特点、优势，在不同行走需求下可以选择相应步态。此节传统步态均设定腰部为正方形构态。

3.1 直行步态

在以往的直行步态规划中，为保证稳定裕度，腿2和腿4 向后平移半个步长。之后按照腿4—腿2—移动身体—腿3—腿1—移动身体的顺序，完成1个周期的直行步态。

自然界中动物爬行多与腰部的扭动相关。因此，当机器人腰部为关节轴线重合状态时，可仿照自然界中动物爬行生成扭腰直行步态。

在扭腰直行步态中，初始站姿如图10(a)所示，实心原点表示机器人重心；然后腰部前部分逆时针扭动，使机器人重心向右下方移动，落在脚2，3与4构成的三角形中，因此，可平稳移动腿1，随后迈动腿2。

图10(e)中，在腰部恢复为原始状态的过程中，将身体向前推动一个步长；腰部后部分逆时针扭动，使重心向左上方偏移，依次迈动腿3、腿4；然后腰部恢复到初始状态，完成1个周期的扭腰直行步态。

接下来从稳定裕度、步长、通过狭窄通道3方面，对传统直行步态和扭腰直行步态进行比较分析。

(a) 直行初始阶段；(b) 直行步态阶段1；(c) 直行步态阶段2；(d) 直行步态阶段3；(e) 直行步态阶段4；(f) 直行步态阶段5；(g) 直行步态阶段6；(h) 直行结束阶段

根据稳定裕度的定义[15]，选择机器人重心在地面的投影到机器人支撑三角形各边的垂直距离最小值为爬行机器人步态的稳定裕度。分别针对2种直行步态迈腿过程进行计算，得到如图11所示的稳定裕度曲线。从图11可以看出：传统直行步态与扭腰直行步态均满足稳定裕度要求，对比之下传统直行步态稳定裕度更大，更满足稳定裕度要求。

1—传统直行步态；2—扭腰直行步态。

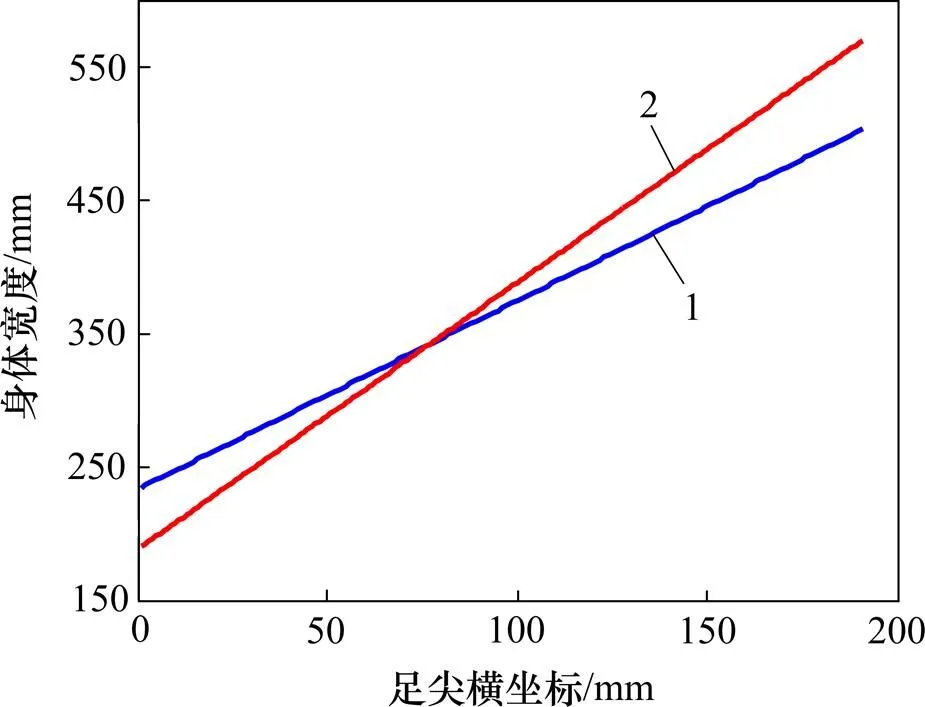
另外，每个步态周期的步长也是直行步态重要的运动特性，传统直行和扭腰直行步长示意图如图12所示。根据第2节中说明的足尖在腿部坐标系中横坐标leg的取值范围，随着腿部髋关节旋转，得到图12所示扇形的腿部足尖工作空间。图12中，1，2，3和4为点，1，2与3为交点。

(a) 正方形构态步长；(b) 关节轴线重合构态步长

传统直行步态初始站姿中，腿1、腿3中腿部髋关节不转动，腿部自然伸长，腿2则在自然伸长的基础上向后移动半个步长，然后在行走过程中向前迈动1个步长。因此，图12(a)中过足尖的竖直线与扇形边界相交，线段1与2中较短的即为半个步长的最大 值，并且此值随着足尖自然伸长的轴坐标的改变而改变。

在−平面中，点1的坐标为

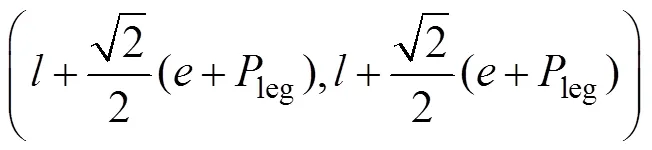
竖直线方程为

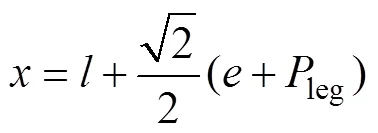
扇形边界方程为

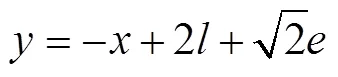
以及

算得竖直线与扇形边界交点，继而可算出交点与点1之间的线段1与2的长度为

图12(b)中，竖直方向为扭腰直行步态中机器人初始站姿，腿部自然伸直，扇形为足尖可达区域。当腰部发生扭动时，足尖位置保持不变，但足尖可达区域发生偏移，从图12(b)可以看出：初始站姿中腿部水平直线到扇形上部分边界的长度即为机器人扭腰直行步态的步长，其最大值为水平直线到扇形顶点的距离。

水平直线方程为

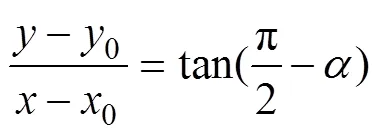
因此，可求出最大步长为

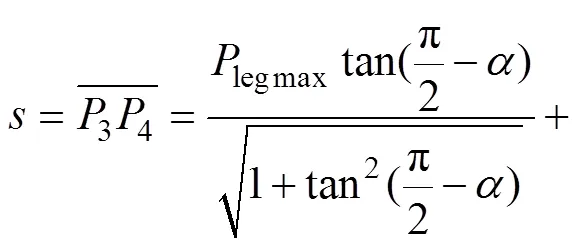
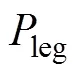
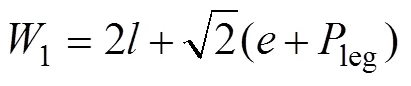
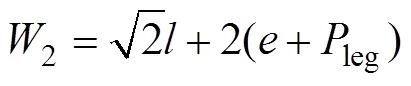
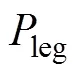
1—W1；2—W2。

从稳定裕度、步长、宽度3方面进行讨论和比较，如表3所示。由表3可知：传统直行步态和扭腰直行步态具有各自的特点，可根据实际需求进行选择。若在直行中需要较大的稳定裕度和行走速度，则可以选择传统直行步态；若需要机器人穿过较狭窄的通道，则可以选择扭腰直行步态。

3.2 原地旋转步态

传统顺时针原地旋转步态中，按照腿2—腿4—腿3—腿1的顺序依次旋转腿部，然后旋转身体完成原地旋转。根据第1节中机器人重心的假设，机器人重心与其几何中心重合，因此，旋转腿2和旋转腿1时，机器人重心落在三角形边界上，为临界稳定状态，在实际情况中，并不能保证行走稳定，因此，需要探索避开临界稳定状态的机器人步态。

表3 扭腰与直行步态比较

利用机器人腰部可变胞的特性，在原地旋转步态中，采用关节轴线重合构态，可通过腰部2杆发生相对扭转使机器人重心偏移，在迈腿时落在支撑三角形内，提高机器人原地旋转步态稳定性。扭腰原地旋转的步骤如图14所示。首先腰部扭动上部分，机器人重心向右下方移动，落在腿2，3和4支撑三角形内，腿1可以平稳旋转；随后依次旋转腿2、腿4及腿3；最后，机器人身体扭动回初始形态，重心回到初始位置完成原点旋转。

针对传统原地旋转步态和扭腰原地旋转步态，在稳定裕度以及活动空间2方面进行对比。

分析2种步态旋转腿时的稳定裕度，见图15。由图15可知：在传统旋转步态中出现了2次稳定裕度为0 mm，为临界稳定状态，并不能保证稳定性；而扭腰旋转步态的稳定裕度一直大于0 mm，满足稳定裕度条件。

将旋转步态的活动空间定义为旋转所需要的圆形区域的半径。传统原地旋转步态活动空间半径为

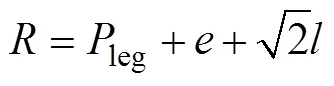
扭腰原地旋转步态活动空间半径为

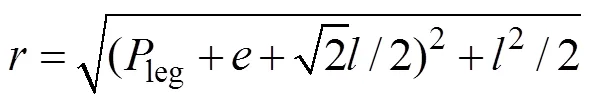
活动空间半径与足尖横坐标的关系如图16所示，经计算可得，传统原地旋转步态最小活动空间半径min=165.6 mm，扭腰原地旋转步态最小活动空间半径min=118.1 mm，即扭腰原地旋转步态可以在更小的空间内完成。

表4所示为2种步态的特点比较，因此，综合稳定裕度与活动空间2方面因素，推荐选用关节轴线重合构态进行原地旋转步态。

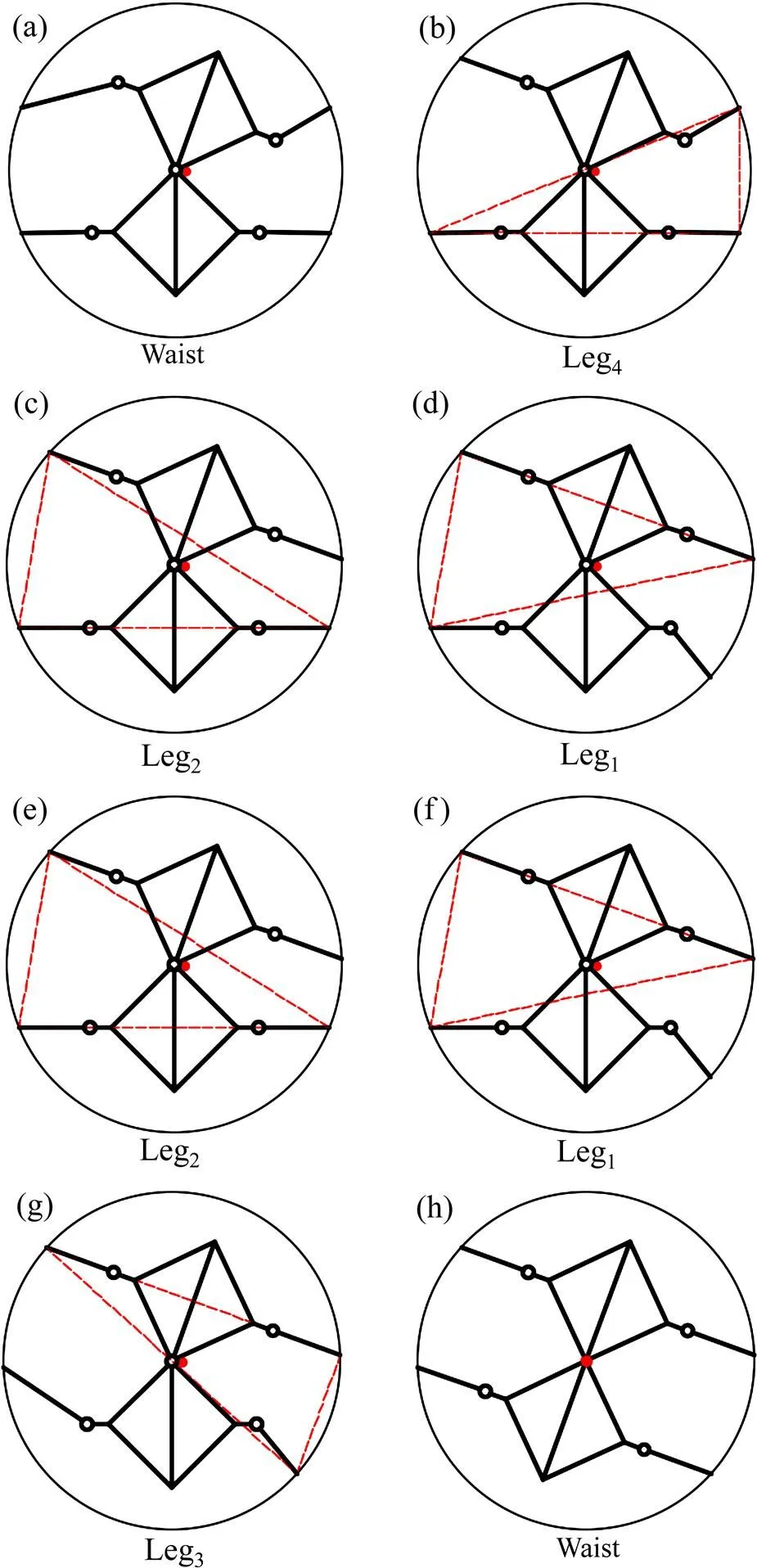
(a) 旋转初始阶段；(b) 旋转步态阶段1；(c) 旋转步态阶段2；(d) 旋转步态阶段3；(e) 旋转步态阶段4；(f) 旋转步态阶段5；(g) 旋转步态阶段6；(h) 旋转结束阶段

1—传统原地旋转；2—扭腰原地旋转。

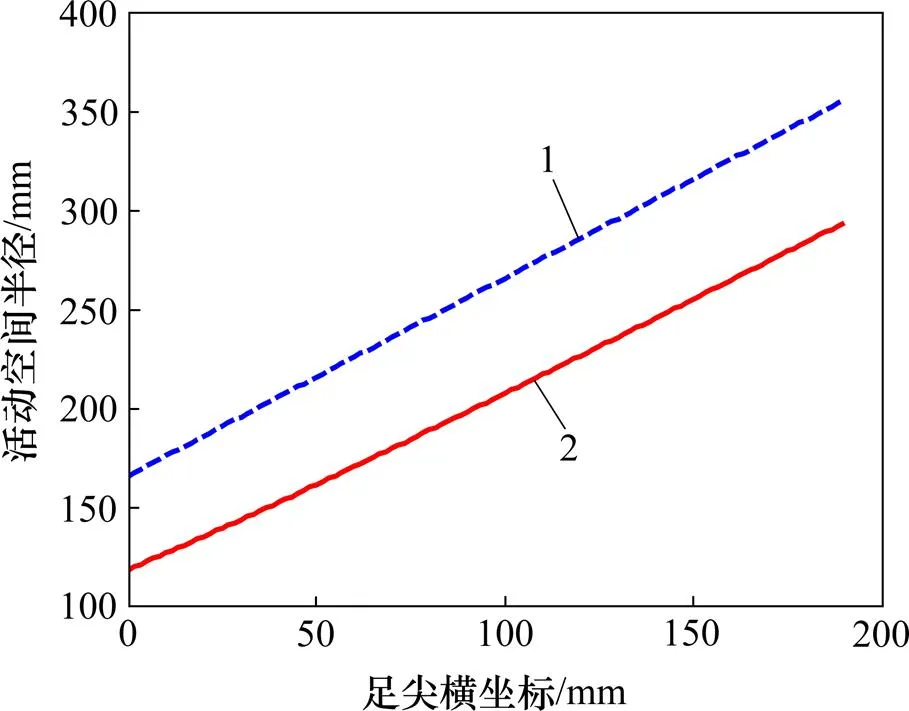
1—传统原地旋转；2—扭腰原地旋转。

表4 扭腰与直行步态稳定裕度和活动空间比较

4 四足变胞爬行机器人运动特性分析

四足变胞爬行机器人腰部可变胞的特征，使其在足尖活动空间、视觉探测等方面具有较明显的应用优势，在实际应用中，能够更好地适应复杂的环境。

4.1 足尖活动空间分析

以足尖可以到达的区域集合来表示机器人足尖的活动空间。当机器人在地面的位置保持不变时，若腰部构态固定，则机器人腿部髋关节的位置也会保持不变，髋关节转动，leg在一定范围内变化，便能确定机器人腿部足尖可到达的位置。当机器人腰部构态可变时，腿部髋关节的位置会随着腰部构态的改变而改变，而髋关节每个位置都对应足尖可达的空间区域。

(a) 正方形构态；(b) 关节重合构态初始位姿；(c) 关节重合构态小角度扭腰位姿；(d) 关节重合构态大角度扭腰位姿

图18 不同腰部构态下足尖活动区域集合

4.2 对机器人视觉功能的影响

在机器人的实际应用中，安装视觉系统能够给机器人提供较为丰富的环境感知信息，提高其智能化程度[16]。机器人依靠视觉传感器(如摄像机)获取信息，识别环境，其可以“看到”的范围便会影响其对环境的识别水平。一般来说，摄像机的视角是一定的，当机器人在地面站立不动时，只能观察到固定范围内的环境，因此，其对环境的感知能力受到限制。

图19 机器人头部摄像头观察范围

5 结论

1) 变胞机构可使爬行机器人腰部构态可变，从而得到变胞爬行机器人。

2) 针对爬行机器人腰部可变的特征，提出扭腰直行步态和扭腰原地旋转步态，其与传统步态各有优势，可根据实际需求选择相应步态。

3) 腰部构态可变使机器人活动空间变大，可以通过更加狭窄的直角弯道，在视觉观察方面也有较大优势，具有较强的灵活性和环境适应能力。

4) 在后续的研究中，将使用运动仿真软件，对机器人的步态规划、稳定性等进行研究，分析影响机器人稳定步行的因素；再利用机器人样机进行步态、稳定性以及环境适应性实验，以便对机器人的实际应用提供参考。

致谢：天津大学现代机构学与机器人学国际中心唐昭、王雁东、崔旭在机器人的机构设计、建模以及样机加工安装等方面作了大量工作，宋智斌、张春松对本论文提出了宝贵建议，在此表示感谢。

[1] 王吉岱, 卢坤媛, 徐淑芬, 等. 四足步行机器人研究现状及展望[J]. 制造业自动化, 2009, 31(2): 4−6.WANG Jidai, LU Kunyuan, XU Shufen, et al. Research situation and prospect on quadruped walking robot[J]. Manufacturing Automation, 2009, 31(2): 4−6.

[2] HIROSE S, MASUI T, KIKUCHI H. TITAN-III: a quadruped walking vehicle, its structure and basic characteristics[M]. 2nd. Cambridge: The MIT Press, 1985: 325−331.

[3] LittleDog: the legged locomotion learning robot[EB/OL]. http:// www.bostondynamics.com/ robot_littledog. html. [2017−08 −17].

[4] RAIBERT M, BLANKESPOOR K, NELSON G. Big Dog, the rough-terrain quadruped robot[C]// IFAC Proceedings of the 17th World Congress. Seoul, Korea: IFAC, 2008: 10822−10825.

[5] LEWIS M A. Self-organization of locomotory controllers in robots and animals[D]. California: University of Southern California. Department of Electrical Engineering, 1996: 87−99.

[6] PARK S H, KIM D S, LEE Y J. Discontinuous spinning gait of a quadruped walking robot with waist joint[C]// Intelligent Robots and Systems. Edmonton, Canada: IEEE, 2005: 2744−2749.

[7] DAI J S, WANG D, CUI L. Orientation and workspace analysis of the multifingered metamorphic hand: metahand[J]. IEEE Transactions on Robotics, 2009, 25(4): 942−947.

[8] 戴建生, 丁希仑, 邹慧君. 变胞原理和变胞机构类型[J]. 机械工程学报, 2005, 41(6): 7−12.DAI Jiansheng, DING Xilun, ZOU Huijun. Fundamentals and categorization of metamorphic mechanisms[J]. Chinese Journal of Mechanical Engineering, 2005, 41(6): 7−12.

[9] 戴建生. 机构学与机器人学的几何基础与旋量代数[M]. 北京: 高等教育出版社, 2014: 380−400. DAI Jiansheng. Geometrical foundations and screw algebra for mechanisms and robotics[M]. Beijing: Higher Education Press, 2014: 380−400.

[10] 甄伟鲲, 康熙, 张新生, 等. 一种新型四足变胞爬行机器人的步态规划研究[J]. 机械工程学报, 2016, 52(11): 26−33. ZHEN Weikun, KANG Xi, ZHANG Xinsheng. Gait planning of a novel metamorphic quadruped robot[J]. Journal of Mechanical Engineering, 2016, 52(11): 26−33.

[11] MÜLLER A. Higher derivatives of the kinematic mapping and some applications[J]. Mechanism and Machine Theory, 2014, 76: 70−85.

[12] 胡斌. 四足机器人结构化地貌典型步态研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2011: 1−8. HU Bin.Research on typical gait of quadruped robot on structured terrain[D]. Harbin: Harbin Institute of Technology.Institute of Mechanical and Electrical Engineering, 2011: 1−8.

[13] 马东兴. 四足机器人步态规划与仿真[D]. 南京: 南京航空航天大学机电学院, 2008: 1−9. MA Dongxing.Gait planning and simulation of quadruped robot[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. School of Mechanical and Electrical, 2008: 1−9.

[14] PARK S, LEE Y J. Discontinuous zigzag gait planning of a quadruped walking robot with a waist-joint[J]. Advanced robotics, 2007, 21(1/2): 143−164.

[15] SANTOS P G D, ENG E G, ESTREMERA J. Quadrupedal locomotion[M]. Berlin: Springer, 2006: 42−50.

[16] 李彬. 视觉地形分类和四足机器人步态规划方法研究与应用[D]. 济南: 山东大学控制科学与工程学院, 2012: 21−22. LI Bin. Research and application on visual terrain classification and gait planning approaches of quadruped robot[D]. Jinan: Shandong University. School of Control Science and Engineering, 2012: 21−22.

(编辑 刘锦伟)

Gait planning and motion characteristic analysis of a metamorphic quadruped walking robot

ZHAO Xin1, KANG Xi1, DAI Jiansheng1, 2

(1. International Centre for Advanced Mechanisms and Robotics, Tianjin University, Tianjin 300350, China; 2. Department of Mechanical Engineering, King’s College, London WC2R 2LS, UK)

To solve the problem of fixed and immutable waists in most walking robots, a quadruped walking robot with a changeable waist was introduced with the structures of the waist and legs being analyzed, and the conditions for waist configuration transformation were presented by using mathematical method. In addition, taking waist action into consideration, two gaits, i.e. twisting forward gait and spinning gait, were designed and compared with traditional gaits to analyze their different advantages in terms of stability margin, motion space and movement through narrow corners. At last, the characteristics in motion space and visual observation of the robot with a changeable waist were researched to demonstrate the environmental adaptability of the designed robot.The results show that the waist configuration of the walking robot can be changed based on the metamorphic mechanism, which can improve the flexibility and environmental adaptability of the quadruped robot.

metamorphic quadruped walking robot; waist configuration; gait planning; motion characteristic

10.11817/j.issn.1672-7207.2018.09.008

TH112

A

1672−7207(2018)09−2168−10

2017−10−03；

2017−11−26

国家自然科学基金资助项目(51535008) (Project(51535008) supported by the National Natural Science Foundation of China)

戴建生，博士，教授，从事机构学与机器人学研究；E-mail: jian.dai@kcl.ac.uk