欠定模型下动态谐波阻抗矩阵的估计
王 亚, 崔 浩, 赵惠咏, 朱英伟
(1. 国网山西省电力公司运城供电公司,山西 运城,044000;2. 国网湖北省电力有限公司襄阳供电公司,湖北 襄阳,441000;3. 四川大学电气信息学院,四川 成都,610065)
0 引言
随着电力系统的发展,大量非线性负荷并入电网,导致谐波污染问题日益严重,如何准确定位谐波源及对谐波责任进行准确划分亟待解决。谐波源定位成为谐波污染责任划分的前提,也是当前国内外研究的热点和难点[1-3]。在谐波源定位过程中,电网的运行方式在不断改变,同时存在一些必要的开关操作,导致电力系统中谐波源信号和谐波阻抗矩阵处于实时波动的状态,从而使得独立分量分析独立分量分析(independent component analysis,ICA)算法难以实现[4-6]。目前,欠定情形下的谐波源定位是一个更符合实际情况的问题[7],要求在谐波电压的量测个数少于谐波源信号个数的情况下进行谐波阻抗矩阵的估计。
文中谐波阻抗矩阵的估计主要采用基于稀疏表征的两步法。但电力系统中当前时刻存在谐波源信号,在下一时刻可能不存在于电网中;或者说当前时刻不存在谐波源信号,在下一时刻可能将突然存在于电网中。此外,环境对电力系统也存在一定影响,所以基于上述情况下的欠定谐波阻抗矩阵估计,常规的两步法已经不能对谐波阻抗矩阵的变化时刻做出准确的判断和估计[8],准确地实现谐波源定位也比较困难。因此,本文对基于欠定模型下动态谐波阻抗矩阵的估计进行了研究和探讨。首先采用稀疏域二维最小偏差角估计谐波阻抗矩阵变化时刻,然后采用重构观测信号采样点搜索方法估计谐波阻抗矩阵和谐波源动态数目,最后对比验证本文方法实现欠定模型下谐波阻抗矩阵变化时谐波阻抗矩阵估计的准确性和合理性。
1 稀疏信号的特征及表示
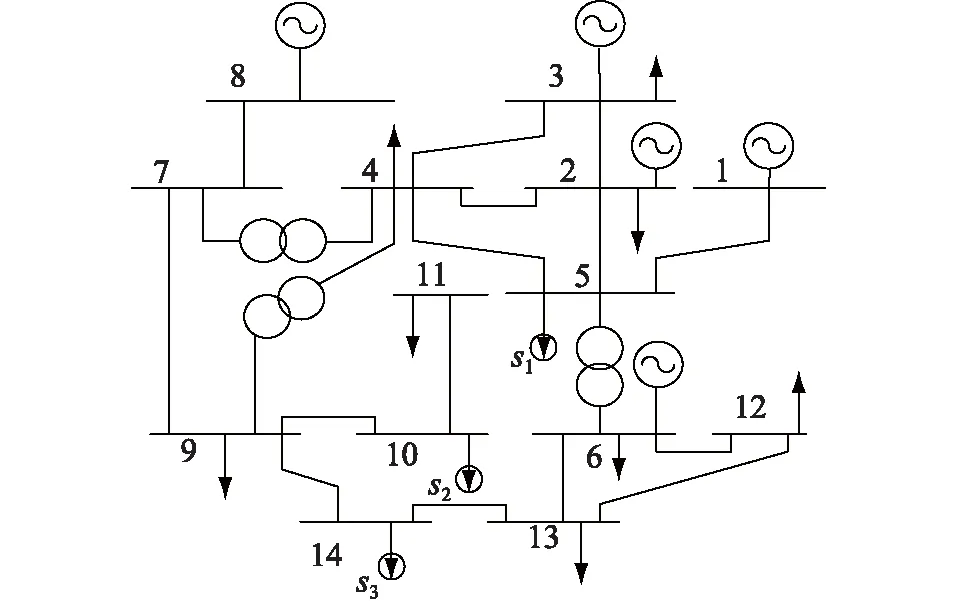
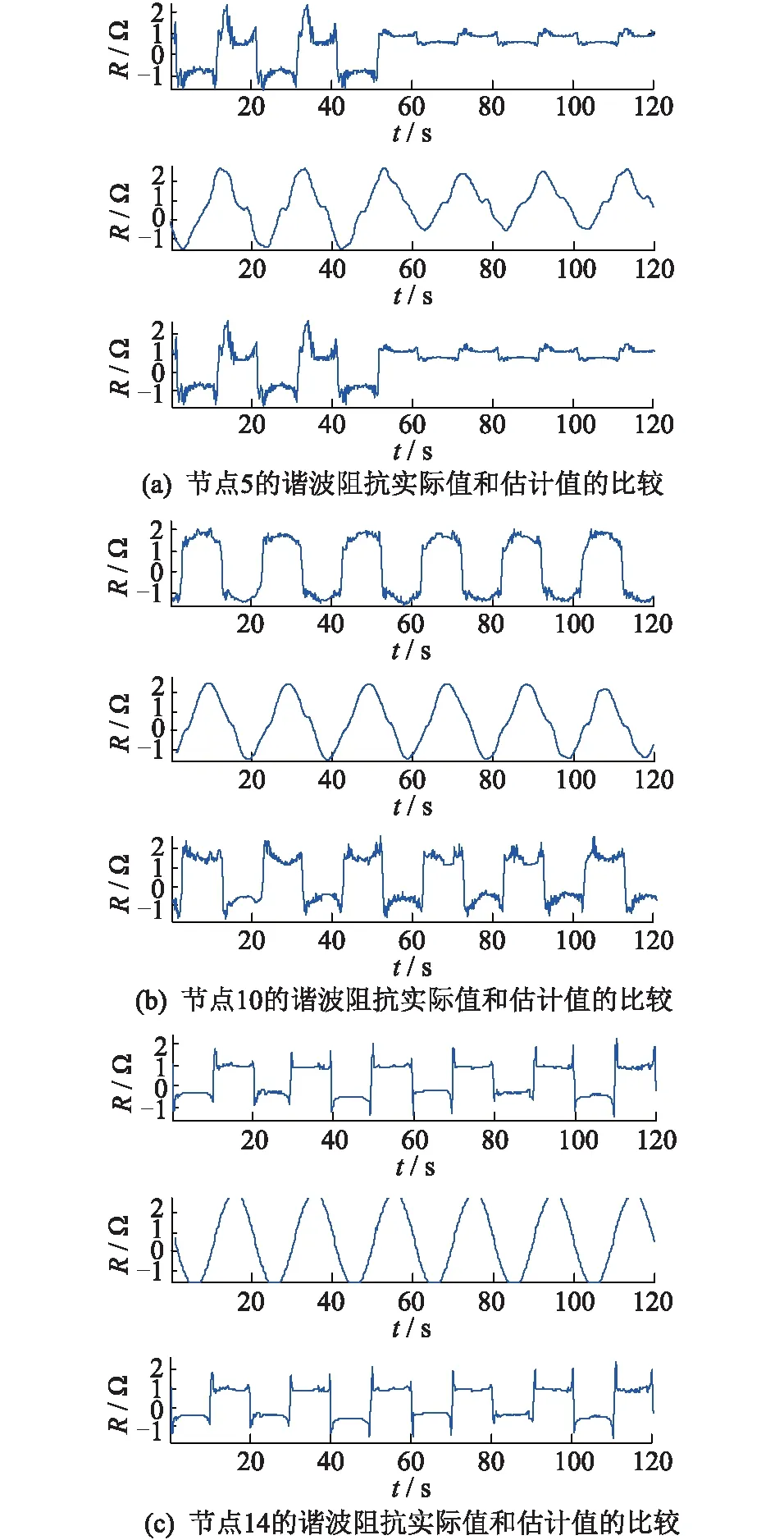
将电力系统中谐波阻抗的估计问题抽象为盲源分离问题[9],在不确定源信号和传输通道的条件下,假设I=[i1,i2,···,in]T是N维相互独立的谐波电流源信号,U=[u1,u2,···,um]T是M维关注母线的谐波电压的量测值信号,Z表示m×n阶的未知阻抗矩阵(m U=ZI (1) 欠定模型下的位于公共连接点(point of common coupling,PCC)节点上的谐波源数量与谐波阻抗矩阵的估计是以信号具有一定的稀疏性为前提的[10]。稀疏信号在多数时刻信号的取值为0,则两个稀疏的谐波源信号几乎不可能同时出现幅值较大的情况,即多数时间段最多仅有一个谐波源信号取值占优。式(1)可以展开表示为: (2) (3) 由式(3)可知,谐波注入电流与量测的谐波电压和动态谐波阻抗矩阵有关。而在估计各节点的谐波注入电流时谐波阻抗矩阵处于随时波动的状态[11],所以首先必须估计出动态变化的谐波阻抗矩阵的变化时刻和变化后的谐波阻抗矩阵。 估计谐波阻抗矩阵最关键的一步是检测其变化时刻[12]。设在t=0,1,…,T1-1,T1时刻,阻抗矩阵为A,在t=T1+1,T1+2,…,T2-1,T2时刻,阻抗矩阵变为B。其中A、B分别是m×p1阶和m×p2阶未知阻抗矩阵,p1,p2分别为t=0,1,…,T1-1,T1时刻和t=T1+1,T1+2,…,T2时刻的谐波源个数,且p1,p2>m。u(t)=[u1(t),u2(t),…,um(t)]T是PCC节点上m个节点的谐波电压量测量。对于t=0,1,…,T1-1,T1时刻,稀疏域中的混合模型可表示为: (4) (5) 对式(5)的各分量做②式除以①式的变换[13],再取反正切变换后得: (6) (7) 定义初始混合矩阵各列矢量的二维方向角为α0(j)(j=1,2,…,n): (8) 由式(6)可知,对i=1,2,…,M的每帧信号的二维观测信号,其在稀疏域采样点中必有一些与初始混合矩阵A的某一列向量具有相同或相近的二维方向角。二维稀疏域最小偏差角可表示为: 同样教授WSET三级的讲师秦岭对此也为学员喊冤:“首先是学员有点冤,考三级也花了不少钱,周期也差不多需要半年时间。但是从WSET的专业角度来说,规矩已经定了,必须要执行。其中最大的问题是学员之间座位分配太近,容易被认为作弊。如果现场非常规范,只是发抖音视频的话,可能只针对机构警告或处罚,并不会针对学生。” δ(k)=min|αi(k)-α0(j)| (9) 在i=1,2,…,M的M帧观测信号中,设定a,b两个阈值[15],a阈值用来判断第i帧观测信号的最小偏差角是否超过a,且超出该阈值的采样点标记num(i);b阈值用来判断超出a阈值的采样点num(i)占第i帧所有采样点数的百分比是否超过b。若判断连续稳定出现超过a的num(i)所占比例超过b值,则认为谐波阻抗矩阵发生波动。 判断了谐波阻抗矩阵的动态变化时刻后,在阻抗矩阵波动前后通过量测不同时刻的母线节点的谐波电压对不同时间段的阻抗矩阵进行估计。以t=0,1,…,T1-1,T1时间段为例,阻抗矩阵A没有发生改变,由(5)得: (10) (11) 在欠定模型下的谐波源定位,需要知道谐波源的数目。针对谐波源数目动态变化的情况,由于谐波源数目与谐波阻抗矩阵的列数相同,为随时波动的变量,采用上述方法估计出某一时刻谐波阻抗矩阵的列数便可以得到动态变化的谐波源数目。 (1) 选取适当的处理域。将谐波电压的量测信号变换到该处理域中,目的是使得谐波电压的观测信号尽可能的稀疏化。 (2) 判断谐波阻抗矩阵是否发生变化。如果没有发生变化,跳转至步骤(3);若谐波阻抗发生变化,使用2.1节的方法判断阻抗发生变化的时刻T1,跳转至步骤(3)。 (3) 采用2.2节的方法对谐波阻抗矩阵及谐波源个数进行估计。 实验仿真使用MATLAB 8.1编程,在图1所示系统上进行测试分析,在持续2 s的时间内对动态谐波阻抗进行估计。谐波电流源设置在节点5,10,14,使谐波源在电气与地理中均相隔较远,其中设置节点5的谐波源在1~2 s内消失。初步选取两个谐波电压的量测节点,关注节点5和10,两个谐波电压的量测节点观测的谐波电压的波形如图2。在欠定模型下对谐波阻抗矩阵的变化时刻进行估计。全部的仿真过程在一台处理器主频为2.33 GHz,内存为2.00 GB的HP计算机上进行。 图1 IEEE-14节点仿真系统Fig.1 IEEE-14 node simulation system 图2 谐波电压的量测节点观测的混合信号的波形Fig.2 Observation waveform of mixed signal of harmonic voltage measurement node 假设在IEEE-14系统中同时注入非线性负荷,其数据来源于New York ISO[17]。信号持续的时间为2 s,采样频率为1000 Hz,取阈值b=50%,分析各帧谐波电压的量测信号的最小偏差角超出一定角度的num(i)在该帧所有采样点中所占比例的变化曲线如图3所示。其中第十帧以后的信号均超过了阈值b,前十帧信号的num(i)都稳定的小于阈值b。故可分析得0~1 s的时间波阻抗矩阵没有发生变化,1~2 s的时间谐波阻抗矩阵发生了变化。 图3 各帧观测信号的num(i)百分比变化曲线Fig.3 Change curve of num(i) percentage of observed signals in each frame 对1~2 s已经发生变化的阻抗矩阵进行估计,设定搜索子区间Q=100。对变化后的某一列阻抗矩阵进行估计,如图4所示。图4(a)表示谐波电压量测值的全部重构采样点组合的散点图;图4(b)表示Q=100的所有子区间内分布的采样点个数;图4(c)表示在重构谐波电压量测信号对区间重新进行分割搜索后采样点的散点图。结合图4(c)的采样数据和公式(11)即能估计出某一列谐波阻抗矩阵,最后再估计变化后的谐波阻抗矩阵。 图4 混合矩阵某一列的估计过程Fig.4 Estimation process of a mixed matrix column 截取谐波阻抗矩阵0~2 s的幅值变化曲线,对比分析实际值、基于稀疏表示的两步算法和基于本文算法估计得到IEEE-14节点系统中节点5、节点10、节点14的谐波阻抗幅值,其分布情况如图5所示。 图5 谐波阻抗的幅值估计Fig.5 Amplitude estimation of harmonic impedance 各节点由上至下的3个波形分别为实际谐波阻抗幅值波形,稀疏表示法估计的谐波阻抗幅值波形和本文算法估计的谐波阻抗幅值波形。采用稀疏表示算法的估计值和本文算法估计得到的谐波阻抗与实际谐波阻抗之间存在误差,但本文算法估计得到的谐波阻抗更接近实际值。图5(a)中,在0~1 s时,稀疏表示法还可以大致估计谐波幅值的变化趋势,但在1~2 s时,实际谐波阻抗幅值变化较小,比较稳定,稀疏表示法完全失真,而本文算法仍能够准确估计谐波阻抗矩阵,同时节点5的谐波阻抗幅值在1~2 s的变化验证了该谐波源在该时段消失。 为了进一步确定本文算法和稀疏表示算法估计的谐波阻抗与实际值之间的误差,表1给出了图5中谐波阻抗幅值的仿真结果,表中的相似系数是描述估计谐波阻抗矩阵和实际谐波阻抗矩阵相似性的参数,定义为: (12) 表1 谐波阻抗估计的相似系数Tab.1 Similarity coefficient of harmonicimpedance estimation 通过表1的相似系数可以看出,从估计精度上比较,在0~1 s时,稀疏表示法和本文算法都能以较高的估计精度估计出谐波阻抗矩阵,本文方法对于节点5、节点14的谐波阻抗矩阵估计精度略高一些;对节点10的估计精度较低一些。在1~2 s时,本文方法仍能以较高的估计精度估计谐波阻抗矩阵,而稀疏表示法估计失败。因此,使用常规的稀疏表示算法是不能适应信源及信道动态变化情况的。从估计速度上比较,本文方法的估计速度约是基于稀疏表示算法的95倍。如果只考虑在混合矩阵未发生变化的0~1 s时段混合谐波阻抗的估计,稀疏表示法虽然能估计出谐波阻抗矩阵,但速度也不及本文方法。在同等仿真环境下,只对0~1s时段混合谐波阻抗的估计仿真表明,稀疏表示法的估计速度是20.370 s,本文方法的估计速度是0.304 s。总之,在本文方法中,由稀疏域中观测信号的一些采样点,可以在判断谐波阻抗矩阵是否发生变化的同时,对动态变化的谐波阻抗矩阵完成估计并获得动态源信号的数目;而稀疏表示法没有对动态变化的混合矩阵采取判断和估计,只是对原观测信号直接进行估计,因此估计失败。 针对欠定模型下电力系统中谐波源信号时而出现时而消失,时变谐波源的数量导致谐波阻抗动态变化的问题,本文提出改进稀疏表征的两步算法估计谐波阻抗。该方法应用到工程实际中的前提是确保每一个待估计的谐波源信号具有稀疏性。该方法的优点是克服了时变谐波源数量对谐波阻抗的影响,可以判断谐波阻抗变化的时刻及精确估计谐波阻抗矩阵。通过MATLAB仿真软件进行IEEE-14节点系统的仿真验证,结果表明,在欠定模型下改进稀疏表征的两步算法估计谐波阻抗具有精确性和合理性,并且在信号的采样点处无需优化,因此本文所提方法比稀疏表示法估计速度快了十多倍。通过本文方法为谐波源定位奠定了基础,比如谐波源定位设备的选型、安装位置等,具有广阔的应用前景。2 动态谐波阻抗矩阵的判断与估计
2.1 动态变化的谐波阻抗矩阵的判断


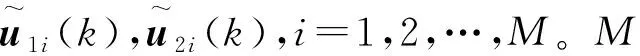
2.2 动态变化的谐波阻抗矩阵的估计
3 欠定模型下动态谐波阻抗矩阵估计步骤
4 仿真实验分析
4.1 仿真模型的建立

4.2 谐波阻抗估计过程


4.3 谐波阻抗的估计结果对比分析


5 结语

