基于改进线路效能的电网脆弱性辨识方法研究

吴 晨， 韩海腾， 祁万春， 张文嘉， 孙文涛， 蔡 晖

(1. 国网江苏省电力有限公司经济技术研究院，江苏 南京 210008；2. 东南大学电气工程学院，江苏 南京 210096)

0 引言

我国的能源资源地理分布与区域经济发展呈现非均衡的特性，西部地区能源资源丰富但经济发展较落后[1-2]，东部及南部经济相对发达但能源资源则相对匮乏，促使我国电网向着长距离、大容量电能传输方向发展。随着特高压和大区互联电网的建设，我国电网已成为一个具有超大规模的复杂系统[3-5]，电网的稳定性问题日趋严重，局部故障的影响范围扩大，进而引起连锁故障，可能引发大面积停电事故[6-9]，造成巨大经济损失和不良社会影响。因此，加强电力系统稳定问题分析，提前辨识电网脆弱环节，有着重要的研究意义，对预防大规模停电事故具有实际的指导作用。

电网脆弱性反映了系统中一个或多个参数的变化对系统安全裕度的影响[10]。通过电网建模和脆弱性评估指标计算，可以从总体上把握电网的薄弱环节，为进一步的电网安全稳定分析提供研究基础，增强电网应对突发事故的能力。

电网脆弱性评估可分为状态脆弱性评估和结构脆弱性评估[11]。状态脆弱性评估[12-15]以电网中各状态变量偏离正常状态及距离临界状态的程度为研究对象，相应的分析方法有能量函数法、灵敏度分析法和基于概率的风险理论分析法等；结构脆弱性评估[16-17]则是以电网中某个单元在网络结构中的重要程度为研究对象，相应方法有基于复杂网络理论的分析方法、关键割集法以及与人工智能相结合的方法等。

电网是一个复杂的网络系统，单一地从运行状态或是网络结构角度进行脆弱程度分析都存在一定的局限，与实际情况相违背[18]。文献[19]定义了综合介数指标，通过加权求和的方法辨识电网脆弱环节，并考虑了节点电压、线路潮流和电网结构的影响。文献[20]用支路抵抗扰动的能力与有向电气介数的比值来定义线路综合脆弱性，同时反映支路本身的抗扰能力及其在系统结构中重要程度。文献[21]基于二维平面拟合的方法分析电网脆弱性，探索运行状态和拓扑特征二者的耦合关系，结合故障线路的有功负载和介数分布进行二维叠加分析。然而，现有文献多是通过数学组合的方法定义综合脆弱性评估指标，并不能完全反映电网的实际运行情况。

本文基于复杂网络理论对电网拓扑结构进行建模，在此基础上，用各支路的有功功率值重新定义了网络线路效能权值，并以此构建了综合脆弱性评估模型，建立同时反映系统运行状态和拓扑结构的综合脆弱性评估指标。

1 基于复杂网络理论的电网拓扑建模

1.1 建模的基本思想和假设条件

复杂网络理论[22]是对复杂系统的抽象和描述。电力系统是一个典型的复杂网络系统，网络包含大量节点，如发电厂、变电站等。同时，网络中各节点相互之间也有着复杂的连接关系。文献[23—24]将复杂网络理论引入电力系统分析中，为电网脆弱性分析提供了新的研究思路。

基于复杂网络理论对电网进行脆弱性评估和脆弱环节辨识，首先须对电网进行简化建模，将电网拓扑结构简化为点线图，其中发电厂和变电站简化为网络中的节点，输电线路简化为网络中的边，以便于研究节点、支路之间的相互关系，找出相对的薄弱环节。在建模过程中，不考虑发电厂、变电站的内部接线，将所有输电线路简化为无向有权边，定义线路电抗值作为每条线路的权重。根据以上建模方法，电网被简化为一个具有n个节点、L条边的点线图。

1.2 电网拓扑特征参数

在建模的基础上，通过以下几个复杂网络特征参数对电网进行描述。

(1) 最短路径。最短路径指从起始的电源节点到终止的负荷节点所有路径中权值和最小的一条路径，即：

(1)

式中：dml表示连接节点m和节点l的支路权值，即该支路的电抗值；R表示节点i和节点j之间任一路径沿线线路的标号集合。

(2) 线路效能。若节点i和节点j之间没有线路直接相连，其线路效能eij为0；反之，当节点i和节点j之间有线路直接连接，其线路效能eij为1。对于所有线路，正常运行情况下eij都为1；在退出运行时，线路效能eij为0。

(3) 最短路径效能。最短路径效能εij是指发电机节点i和负荷节点j之间连通最短路径的线路效能的倒数和的倒数，即：

(2)

式中：S表示节点i和节点j之间最短路径沿线线路的标号集合。最短路径效能反映了发电机节点与负荷节点间的电能输送能力，路径的效能越大，电力传输能力越大。

(4) 系统全局效能。系统的全局效能E定义为网络中所有发电机节点与负荷节点之间最短路径效能的均值，其定义为：

(3)

式中：εij表示节点i，j间的最短路径效能；NG表示网络中发电机节点总数；NL表示网络中负荷节点总数。

系统全局效能反映了整个网络的电能输送能力，系统全局效能越高，整个系统的电能传输容量越大。

2 线路效能定义的改进

在建模过程中，仅从电网的拓扑结构考虑网络的电能输送能力是不全面的。网络的传输能力与系统的运行状态有着密切联系，当电网受到扰动或发生故障后，节点电压，支路潮流等状态变量发生变化。在系统中无功充裕的假设下，发生扰动时，线路的无功传输量变化很小，可以忽略不计。根据潮流计算公式，系统中任一支路的有功输潮流为：

(4)

式中：Pij为支路当前有功传输量；Vi和Vj分别是节点i和节点j的电压幅值；Bij为支路电纳；Gij为支路电导；δij为节点i和节点j的电压相角差。

重新定义后的线路效能eij表征如下：

(5)

改进后的eij是[0,1]区间内的值，相较于原先简单的布尔值，更加具有实际意义，可以定量描述支路的有功传输状态。当线路效能为1时，表示该线路有功功率达到支路最大传输功率，线路输送能力得到充分利用；当线路效能为0时，表示此时线路传输有功为0，线路并未发挥传输潮流的作用。

3 电网综合脆弱性评估指标

当电网运行状态偏离正常工况时，线路传输功率也将随之变化；另一方面，当电力网络发生故障时，由于线路元件自身原因或是继电保护装置的动作，部分元件从网络中移除，会导致网络的拓扑结构和运行参数发生变化，从而引起最有效路径的重新分布。系统运行状态或结构发生变化后，系统全局效能的变化量ΔE为：

ΔE=E0-E′

(6)

式中：E0表示初始系统全局效能；E′表示电网结构变化后系统全局效能。

将全局效能的变化作归一化处理，定义电网综合脆弱性指标C为系统全局效能变化量ΔE与系统初始效能E0的比值，即：

(7)

其中：

(8)

(9)

4 算例分析

为验证综合脆弱性评估指标的准确性和有效性，本文采用IEEE-30节点标准算例进行仿真分析，图1为测试系统的网络结构图，其中包含6台发电机，分别位于节点1(平衡节点)、2、5、8、11、13；初始支路共41条，支路编号分别为1～41。

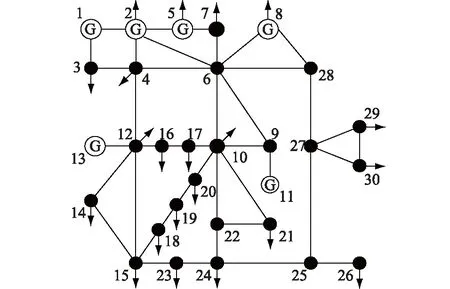
图1 IEEE-30节点网络拓扑图Fig.1 Topology of IEEE-30bus system

4.1 电网脆弱节点辨识

首先通过仿真分析发电机出力和负荷变化对电网综合脆弱性的影响，辨识电网脆弱节点。保持网络结构不变，2、5、8、11、13节点发电机节点出力增加50 MW，各负荷节点的有功需求依次分别增加50 MW时的系统脆弱度如图2所示。

图2 节点脆弱度曲线Fig.2 Nodal vulnerability curves

结果表明，负荷节点26、29、30节点的脆弱程度最高，由网络拓扑结构可见，上述节点均处于电网末端，供电距离远，因此易于受到潮流波动的影响。当末端节点负荷需求增加时，网络的整体脆弱度大幅度增大，接近于1的临界值，可见末端节点负荷的稳定非常重要；其次，负荷节点3和4的脆弱程度也相对较高，两者均是网络的重要枢纽，其本身负荷需求量大且是网络中多条最有效路径的关键节点，当节点负荷需求增大时，邻近线路负担加重，导致网络整体脆弱度增加。由此可见，对于一个电力网络而言，末端节点和重要枢纽节点对网络整体脆弱性指标影响较大，对这些节点应加以重视。

4.2 电网脆弱线路辨识

4.2.1N-1故障下的电网综合脆弱性分析

将网络中41条支路分别断开，进一步研究电网综合脆弱性指标的变化情况，支路依次断开时的综合脆弱度曲线如图3所示。结果表明，一些与电源连接紧密的线路，如支路L2,5、L1,2、L1,3，L3,4(Li,j表示连接节点i和j的线路)在网络传输中起着非常重要的作用，需要格外重视。

图3 N-1故障下的综合脆弱度曲线Fig.3 Vulnerability curves under N-1 scenarios

4.2.2N-2故障下的电网综合脆弱性分析

相同条件下，采用电网连通率指标辨识出的脆弱支路为L1,2、L1,3、L3,4、L2,6、L4,12，与本文建立的综合脆弱指标评估结果基本一致。除上述支路外，本文建立的指标还能辨识出L12,13、L9,11等电源并网线路以及对整体网络潮流分布影响较大的支路(例如支路L2,5)，更加符合实际电网情况。

图4 N-2故障下的综合脆弱度曲线Fig.4 Vulnerability curves under N-2 scenarios

5 结语

本文基于复杂网络理论对电网进行抽象建模，用线路输送功率改进了传统线路效能权值的定义，再通过最短路径计算方法，求取了系统全局效能以及系统运行状态或结构改变后的全局效能变化量，以此建立了电网综合脆弱性评估指标，并分别对电网中节点和线路脆弱环节进行了辨识。仿真结果表明，电网中与周围连接紧密的枢纽节点、位于电网末端的节点以及与电源连接紧密的线路多为整个网络中的脆弱环节。因此，在实际电网运行中，对于重要枢纽变电站和终端负荷变电站，需要加强运行监控以及风险防控，从而提高电网安全稳定水平。由于本文提出的综合脆弱性评估指标不仅能定位系统的脆弱节点和脆弱支路，还能评估电网在某一特定状态下的整体脆弱程度，因此在坚强电网的规划建设方面具有实际应用价值。