四边形网格自动生成方法改进及工程应用

徐 青，奚鹏飞

(武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

随着计算机技术和数值分析理论的发展，有限单元法在工程结构分析中的应用越来越广泛。有限元网格划分是有限元分析前处理的主要工作内容，其复杂性及鲁棒性一直以来都是有限元分析的瓶颈问题，一定程度上影响着有限单元法的推广应用和发展[1]。

网格生成方法有结构化网格生成方法和非结构化网格生成方法。结构化网格生成方法主要有坐标转换法、Paving法等，生成的网格质量好，但仅适用于简单域，一般用在流体动力学分析中；非结构化网格生成方法主要有八叉树法(Octree method)、Delauney法、Octree/Delauney法以及行波法(advancing front method)等，生成的网格质量要求宽松，可适应复杂域，主要用于结构数值分析中[2]。对于自由曲面网格的划分与优化，也有学者开展了专门研究[3,4]。

坐标转换法[5]是通过坐标转换，将不规则域转换成规则域，在规则域上进行网格生成，然后转换回不规则区域。Paving法[6]是由边界向内部逐排生成单元，对边界的适应性较强，但域内单元密度由边界决定，难以生成梯度变化较大的网格。八叉树法[7]是先将研究域划分为子域，实现对复杂边界的分解，再按照一定的要求划分成单元。该法可以实现对网格生成进程的控制，边界适应性强，离散区域的几何拓扑关系不变，但八叉树法仅仅是一种边界简化方法，不是一种真正的网格生成方法，须依赖于其他的网格生成方法。Delauney法[8]概念简单，易于实施，可以得到网格尺度场梯度变化较大的网格，但边界和域内会生成可能引起计算问题的点，以及得不到所需网格密度等问题。1987年，Peraire等人提出了行波法[9]。行波法是在生成结点的同时生成单元网格，应用背景网格存放离散所需要的信息，能够很好地控制所生成的四面体单元的形状。

陈胜宏等在进行系统的自适应有限单元分析时，采用行波法实现了二维四边形、三维四面体及三维六面体网格自动离散[2,10-12]，编制了core-AFEM系列软件。本文基于已有研究成果，针对水工建筑物中具有水平边和铅直边的薄层构造及其他复杂边界，在进行网格自动划分时可能出现异常中断等问题，探讨二维四边形网格自动生成的优化及改进方法，提高程序的鲁棒性，优化网格质量。

1 平面四边形网格生成

水工结构及岩土工程，其研究区域通常由多种材料构成，且存在断层、软弱夹层、防渗墙等薄层结构，以及廊道(孔洞)等，使得网格划分形状不规则，随机性较大。针对这些特点，网格生成的总体思想是，将多介质复杂区域转换为若干由单一介质构成的子域，每一子域单独生成网格，由各子域的网格组合成复杂区域的网格。

图1为四边形网格划分流程，主要技术特点是包含节理边处理、边界离散、三角单元生成过程中节点选取、三角形合并为四边形的控制过程，以及网格质量的初步优化。

1.1 区域描述

计算域由子域、边界和节点3级数据结构进行描述。首先根据材料分区和结构分区，将复杂区域分解成若干个简单的子区域，由边界线描述子区域，再由节点构造边界线，最后把由边界线描述的子区域转换为由其边界节点描述。边界节点按逆时针方向排列，区域位于节点排列方向的左侧，逆向排列的节点封闭环唯一确定了区域。

1.2 背景网格

背景网格是一套覆盖全部区域的尺度网格，用于给定区域内单元尺寸的分布信息。网格上每一节点给定了该点的相邻单元尺寸，区域内任一点的相邻单元尺寸由该点所在的背景网格单元插值确定。

1.3 边界离散

边界线准备数据文件中，边界点是区域几何形态等发生变化的点，一般不直接用于网格生成，而是依据背景网格，先离散边界线，增加节点数。对于任意线段，其上任意一点的尺度可由该点所在的背景单元内插确定。设δ(l)为单元尺寸沿边界线l的分布函数，L为l的长度，边界节点加密后边界线l的线段数N取与N′最接近的整数，N′由下式计算得到：

(1)

子域内生成全四边形网格的必要条件是：边界节点数必须是偶数。对于任一子区域，选取一个最长待划分边，通常是划分份数最多的普通边，该划分边的划分份数可能会增减1，以保证总节点数为偶数。

1.4 节理处理

研究域中存在节理、防渗墙等薄层结构时，统一定义其中线为节理边。先对边界进行离散，再根据薄层结构的厚度t，生成节理单元，如图2所示。

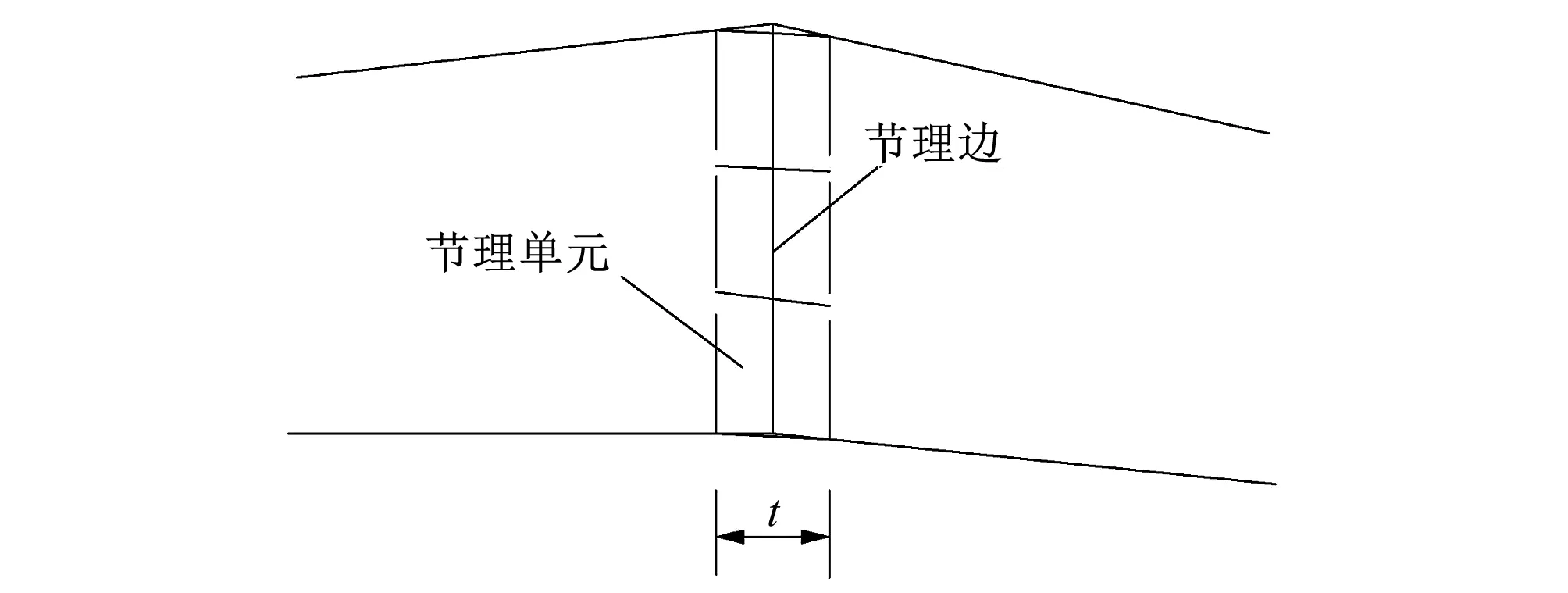
图2 节理单元生成Fig.2 Joint element generation

1.5 网格生成

网格自动划分算法以三角形单元生成为基础，设置四边形单元的状态参数，在一个三角形单元基础上生成相邻三角形单元，从而构成四边形单元，完成全域的四边形网格划分。

新生成的单元需进行单元质量控制，主要包括有效性检验、单元形状控制和奇异性检验。若有一项为否，则跳到下一节点再次判断。若全部满足，则该节点与活动边形成新的三角形单元。

1.6 网格质量控制

(1)有效性控制。网格生成过程中，需对其有效性进行控制，新生成的三角形网格不能穿过已生成的四边形网格，以保证网格的合理性和有效性。

(2)四边形内角控制。四边形单元的最优形式是正方形，因此控制四边形的内角可以对网格的质量进行基本控制，本程序中控制四边形的各内角不大于120°。若不满足，则判定网格质量为不合格。

(3)奇异单元控制。对于边界单元，尤其是在边相邻的区域单元，可能会出现三边四结点的三角形奇异单元，对此本文通过控制四边形单元中各边节点数不超过2来避免此类单元的产生。

1.7 网格质量优化

对于复杂域，通常会出现自动生成的网格质量不高的现象，因此需对网格进行优化。优化方式包括节点位置优化和拓扑关系优化2种。

1.7.1 节点位置优化

节点位置优化是通过保持网格拓扑关系不变的情况下改变节点的位置，以此来提高网格质量的一种技术。其中最经典的是拉普拉斯光滑算法，该算法简单，且耗时短。

节点位置优化通过调整网格单元内部的节点或者表面非边界节点实现。假设要移动的节点为K，优化后的K点坐标为：

(2)

式中：Ni为该节点所在单元内的其他节点总数。

1.7.2 拓扑关系优化

当网格局部区域有一些节点的度值不理想时，无法仅通过移动节点的位置来提髙网格的质量，需要先改善网格的拓扑结构，才能更好地提髙网格的质量。

网格的边界节点是不变的，因此拓扑关系优化主要针对内部节点进行。对四边形网格而言，内部节点的相邻单元个数NE最好等于4。当某一个内部节点的相邻单元个数NE比4大或小很多时，环绕该节点的单元则会产生较大的畸变，此时应进行调整。调整方法主要有(见图3)。

(1)节点删除[图3(a)]。如果内部节点A的相邻单元数NE=2，则节点A将被删除。

(2)单元删除[图3(b)]。如果某单元的2个相对节点A、B都是内部节点，且NE(A)=NE(B)=3，则删除该单元。

(3)对角线交换[图3(c)]。由于四边形网格中每个节点所在边的个数NE等于4时，网格质量最优。因此，首先检查由2个内部节点连成的边AB，若NE(A)+NE(B)≥9，再检查以AB为边的2个单元组成的六边形AEDBFC中其他对角线的2个节点是否更接近最优。有3种情况：当[NE(A)+NE(B)]-[NE(C)+NE(D)]>[NE(A)+NE(B)]-[NE(E)+NE(F)]≥3时，则用CD代替AB；当[NE(A)+NE(B)]-[NE(E)+NE(F)]>[NE(A)+NE(B)]-[NE(C)+NE(D)]≥3时，则用EF代替AB；否则不进行对角线交换。

(4)边删除[图3(d)]。检查所有2个内部节点连成的边EF，若NE(A)=NE(B)=3，且含有EF边的2个相邻单元中没有边界边，则删除边EF。当NE(A)+NE(D)≤NE(B)+NE(C)时，用AD作为新的替代边；否则用BC作为新的替代边。

图3 拓扑优化示意图Fig.3 Pattern of topological optimization

2 四边形网格自动生成算法改进及优化

在坝工工程中，防渗墙是常用的工程措施，与大坝相比，防渗墙属于薄层结构；同时，坝基岩体通常存在着各类软弱夹层。本文针对具有水平边或垂直边的薄层单元等，提出四边形网格生成改进方法，以提高算法的鲁棒性，并进一步优化网格质量。

2.1 四边形网格生成算法改进

2.1.1 网格嵌入

网格嵌入或交叉是网格生成过程中最为常见的情形，通常是由于算法逻辑没有考虑到某些特殊情形(如具有水平边或铅直边的薄层单元)，交叉判定时产生错误，从而影响网格鲁棒生成。

(1)水平薄层单元。如图4所示，N1、N2为当前活动波前，(X,Y)为可能的新单元点。首先考察点P是否满足新点要求。从图4可以清晰地看到，点P与N1、N2构成的新三角嵌入到已生成单元中(图4中阴影部分)，不满足网格的有效性要求，故应排除该点，并进入下一阶段新单元点选取。

图4 新单元点嵌入相邻单元中Fig.4 New node inserted into adjacent element

引起该嵌入发生的原因是：线段PM与线段BN1的交叉判定出错。在计算交点J的过程中，由于舍入误差的存在，计算所得的J点纵坐标Y可能出现无限接近却不等于点P和点M的纵坐标的情况(PM是一水平线)，导致J点被认为不在PM上，从而该三角单元被允许生成，形成嵌入。对于由于计算误差产生的线段相交误判，本文提出的改进方法是：对线段相交模块进行优化，在直线相交子程序中，当存在水平边时，直接用水平边的纵坐标指定交点Y值，再计算交点X值，从而避免线段相交误判。

(2)铅直薄层单元。如图5所示，N1、N2为当前活动波前，虚线为节理边。点P为可能的新的单元点。考察点P是否满足新点要求，从图5可以清晰地看到：P与N1、N2构成的新三角嵌入到节理单元中，不满足网格的有效性要求。

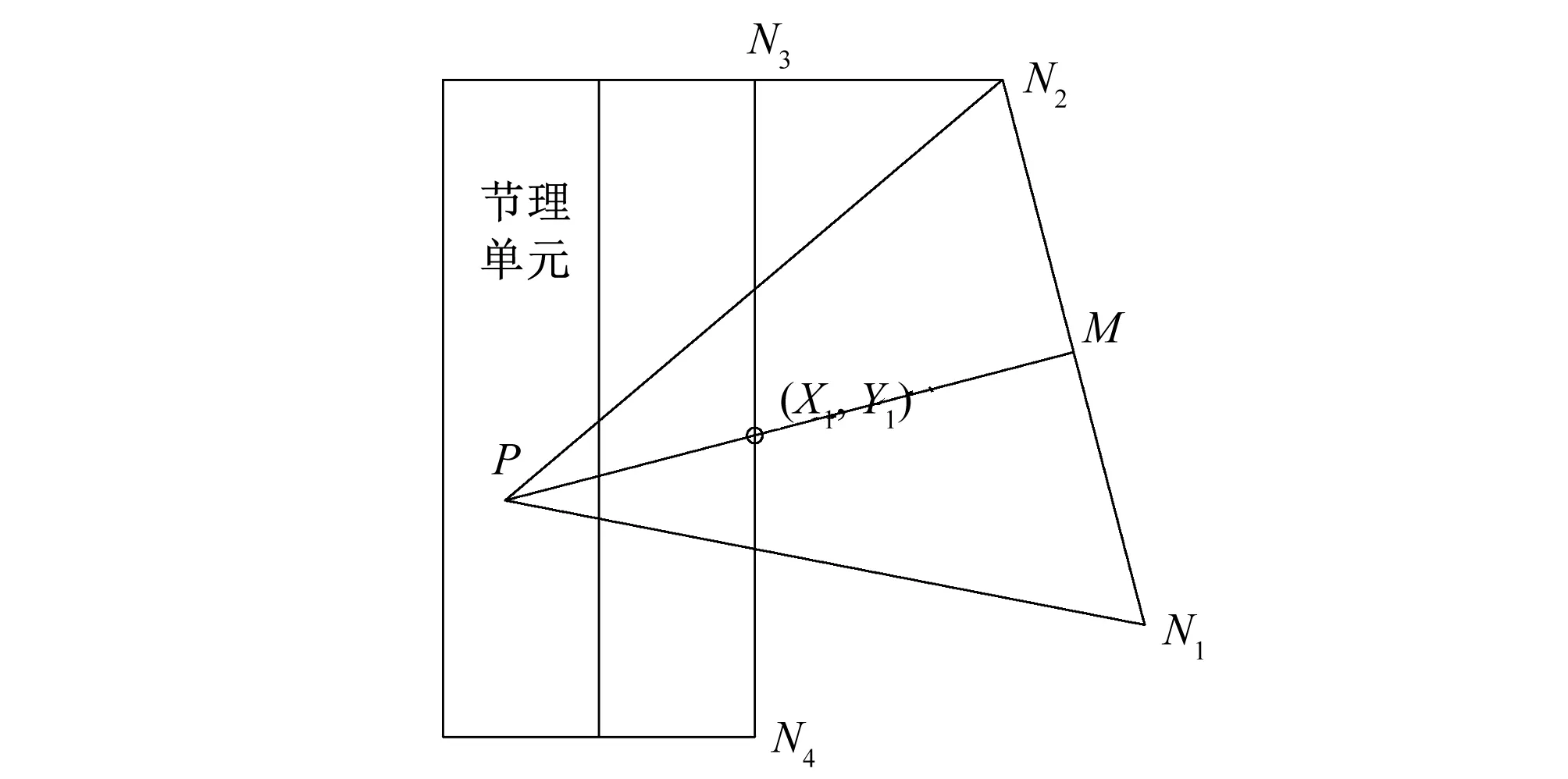
图5 新单元点嵌入节理单元中Fig.5 New node inserted into joint element

引起该嵌入发生的原因是：线段PM与线段N3N4的交叉判定出错。这里存在2次舍入误差。第1次舍入误差是N4的坐标计算，N4是节理扩展边上的节点。在计算该点横坐标的过程中，由于舍入误差的存在，使得计算得到的节点N4的横坐标也是与N3横坐标十分接近的一个数值，因此N3N4线段的节点斜率绝对值极大。第2次舍入误差来源于PM与线段N3N4计算所得交点横坐标，十分接近，但是不相等，计算纵坐标时由于斜率极大，使得纵坐标与理论结果相差较大，得出相交节点不在N3N4上的结论，从而生成嵌入单元。

2.1.2 内部断层单元处理优化

在有限元数值模型建模阶段，常常将内部节理边延伸至模型边界，这样不可避免地会影响周围区域的波前，使网格划分更加密集，增加网格数量，见图6。

图6 断层边延伸至边界Fig.6 Extend the joint edge to the boundary

本文对内部节理边的处理提出如下优化方案。

(1)对节理边不进行延伸。将节理边细分，并生成节理单元，同时更新节理边相邻的边端节点。

(2)对边界与节理边垂直的面域B和E，检查面域的连续性。这种面域在节理单元生成、节理边端点更新后，面域端点更新为节理单元两端，整个面域波前不再连续。

(3)增加补充边。增加边12和边34，如图7所示。将该补充边默认为已划分状态，避免被后续可能的边界加密，产生额外的节点，破坏已生成的节理单元。

(4)为避免补充边的生成引起受影响面域的波前总节点数由偶数变为奇数，四边形网格自动生成的前提条件不满足，使得网格划分失败，须将操作过程与边界离散操作的顺序进行交换。

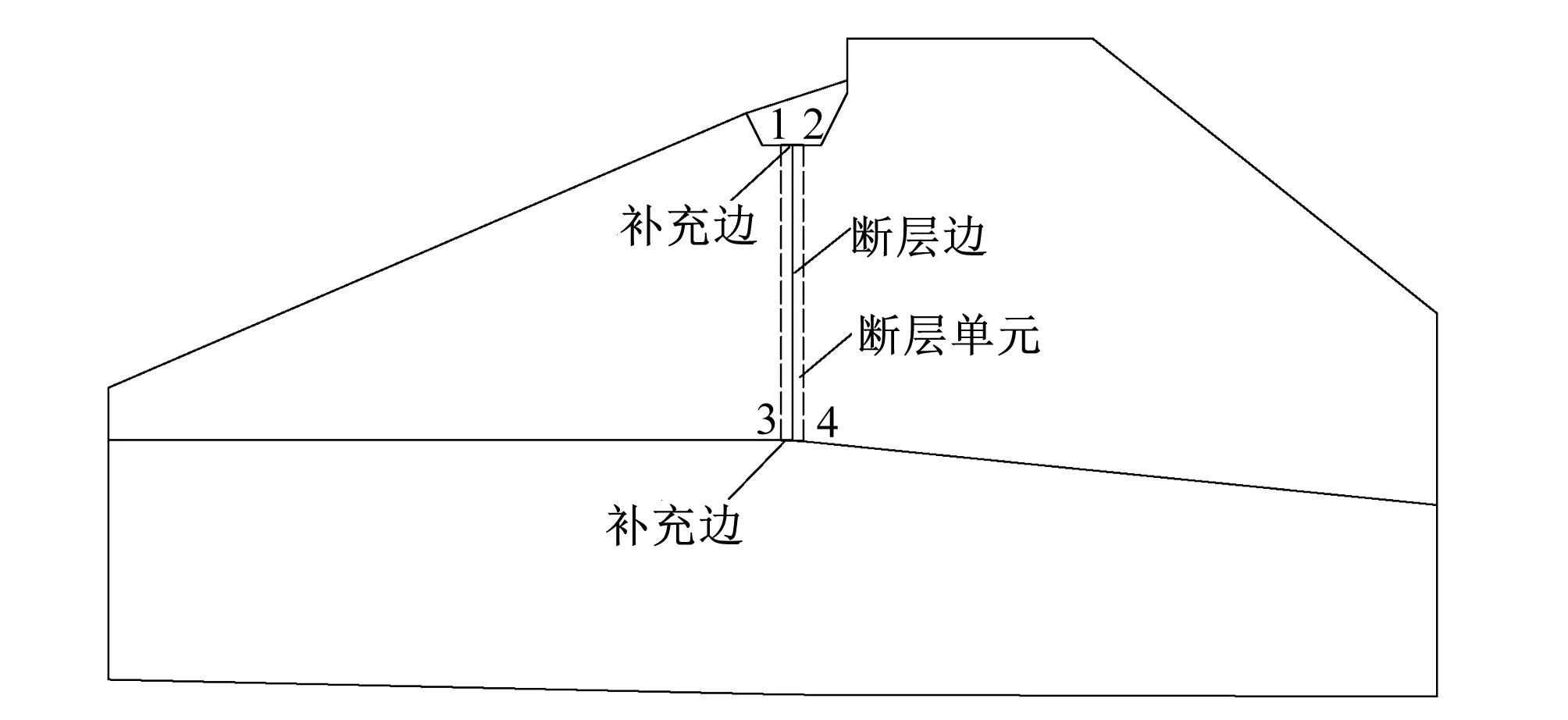
图7 补充边示意图Fig.7 Supplementary side

2.2 网格质量优化改进

在网格质量优化的过程中，网格拓扑关系发生改变，从而影响周围网格的拓扑关系，可能会产生新的不良单元。对此，本文提出了相应的优化方案。

如图8所示，由图8(a)到图8(b)，表示拓扑关系优化中的节点删除，但由于该操作又产生了新的低质量单元，且单元中存在边界节点，拓扑关系优化操作受到限制。改进思路是：从单元的内部节点入手，调整节点A至节点C，将该单元直接删除，如图8(c)所示，周围单元拓扑关系不变，网格质量得到优化。

图8 边界三角单元处理Fig.8 Treatment of singular element on boundary

3 工程应用

本文选取具有复杂地质构造，并设置有混凝土防渗墙的土石坝剖面，如图9所示。将其分为16个面域，80条边，65个端点。各区域材料的渗透系数如表1所示。由于逸出点处及混凝土防渗墙处渗透坡降较大，表1中也给出了相应材料的允许渗透坡降，用以判断土石坝的渗透稳定性。

图9 土石坝剖面(单位：m)Fig.9 Section of an embankment dam

依据上述改进方法，四边形网格自动划分过程顺利，网格质量良好，如图10所示。

采用课题组开发的软件core-AFEM/seep2对该土石坝进行渗流分析，坝体自由面、等水头线及渗透坡降、流速如图11～图13所示。计算结果显示：①自由面及各渗透特性分布规律符合常规；②J混凝土防渗墙≤40，J二期填土<0.48，vmax<10-6m/s，说明满足渗透稳定要求，与实际工程状况相符。

表1 各区域材料渗透系数Tab.1 The permeability coefficient

图10 四边形网格划分结果Fig.10 The quadrilateral mesh

图11 等水头线分布Fig.11 The equipotential line distribution

图12 渗透坡降分布Fig.12 The seepage gradient distribution

4 结 语

本文基于行波法，针对具有水平边和铅直边的薄层单元(如混凝土防渗墙、断层等)，提出了二维四边形网格自动划分改进方法，提高了网格自动生成的鲁棒性，并经工程应用检验，可以很好地应用于有限元数值分析，并具有网格划分合理、易于掌握等特点，极大地提高了网格自动生成的适用范围。

图13 流速分布Fig.13 The flow velocity distribution

□