基于HAR-Copula模型的沪港股市动态相关性研究———“沪港通”实施背景及高频数据视角

刘光强

(西南交通大学经济管理学院,四川 成都 610031)

一、引 言

利用高频数据度量金融资产的波动率在信息含量、模型构建及参数估计等方面均具有重要优势，成为近年来的研究热点。Andersen 和Bollerslev 、Barndorff-Nielsen 和Shephard 提出的已实现波动率方法(Realized Volatility，RV)，通过利用积分波动率(Integrated Volatility)估计RV为高频波动研究奠定了基础。Corsi提出的具有长记忆的异质自回归模型(Heterogeneous Autoregression，HAR)克服了前期分整模型(ARFIMA)在计算复杂性等方面的不足，成为研究RV模型的重要思路[1-2]。在此基础上，将总波动分为连续性波动和非连续性波动(跳跃)，Gallo和Otranto借助Barndorff-Nielsen和 Shephard所提出的二次变差理论，衍生出了跳跃型HAR模型(HAR-with-Jumps，HAR-J)和连续型HAR模型(Continuous-HAR，CHAR)。而Patton 和 Sheppard[3]通过对总波动进一步分析，考虑其正向波动和负向波动的不同影响，建立了Semivariance-HAR模型(SHAR)。

目前，应用相关高频波动率建模主要集中在探讨RV的预测，如陈浪南和杨科[4]利用上证综指2000—2008年的高频数据实证检验了中国股市高频波动率的特征，并综合分析了相关模型的样本外预测能力。宋亚琼和王新军[5]则重点考虑了对跳跃强度的拟合，其结果表明跳跃强度对RV具有显著影响。瞿慧和程思逸[6]考虑宏观信息发布因素对沪深300指数的影响并对其RV进行建模。由此可见，从基础的HAR类模型所衍生出来的考虑了跳跃成分的相关建模取得了理想的实证效果。

现有高频波动建模的文献大多局限于对波动率本身的探讨，而缺少进一步对波动率建模在风险管理等方面的深入研究。本文拟结合HAR理论与Copula理论，并以沪港股市为研究对象，对沪港股市两者间的相互关系展开分析。提出这一研究设想主要基于：(1)现有文献在探讨股市之间相互关系时往往应用日数据，而较少利用高频交易信息，如龚朴和李梦玄[7]探讨沪港股市的波动溢出和时变相关性时采用的是沪港股市间的日数据，刘镜秀等[8]利用了1991—2011年的日数据对中外股市间的动态相关性进行了实证研究。(2)Copula理论对两个时间序列间的相关性具有很好的拟合效果，但将HAR与之相互结合的相关研究还比较少见。如李强和周孝华[9]利用Copula函数对我国台湾和韩国股票市场相关性展开了实证分析，黄在鑫和覃正[10]基于Copula理论对中美主要金融市场相关结构及风险传导路径进行了研究。(3)虽然目前已有学者以“沪港通”为背景展开了相关研究，如蔡彤彤和王世文[11]等，但公开的文献中未有同时将HAR模型与Copula理论相结合展开的分析。

二、相关理论

(一)高频波动率理论

若假定资产的价格为p，那么，其价格的微分方程服从：

dlog(pt)=μt+δtdWt

(1)

也就是说，价格微分方程为连续波动μt和瞬时波动过程δt与布朗运动Wt之间的乘积，这里分析基于不考虑是否有跳跃情况，考虑跳跃的情形将在以下内容中进行阐述。在对RV研究过程中，现有文献均是为了如何准确预测未来时间之内的积分波动率(Integrated Variance，IV)，IV为：

(2)

但IV无法直接观测，常用已实现波动率(Realized Variance，RV)代替，RV为：

(3)

也就是说，RV表示在时间t内所有收益率的平方和，而M=1/Δ表示在交易频率Δ下时间t内的所有交易总次数，rt,i=log(Pt-1+iΔ)-log(Pt-1+(i-1)Δ)。当Δ→0时，RVt的估计误差可以表示为：

RVt=IVt+ηt， ηt～MN(0,2ΔIQt)

(4)

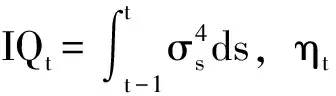
(5)

HAR模型是当前对RV建模的重要基础，HAR模型为：

RVt=β0+β1RVt-1+β2RVt-1|t-5+β3RVt-1|t-22+ut

(6)

在基础的HAR模型上，通过对总的波动率进一步分解，若考虑了跳跃情形的HAR-J模型。也就是说，在HAR模型的基础上，增加了跳跃因子，则有：

RVt=β0+β1RVt-1+β2RVt-1|t-5+β3RVt-1|t-22+βJJt-1+ut

(7)

其中，Jt=max[RVt-BPVt,0]，BPV为：

(8)

除了考虑跳跃情形外，仅仅考虑非跳跃，也就是仅仅考虑连续模型CHAR被定义为：

RVt=β0+β1BRVt-1+β2BRVt-1|t-5+β3BRVt-1|t-22+ut

(9)

另外，Patton 和 Sheppard[3]在Barndorff-Nielsen等所提出的半方差测度基础上，通过对总的波动进一步分解为正向波动和负向波动提出了半方差HAR模型(Semivariance-HAR，SHAR)：

(10)

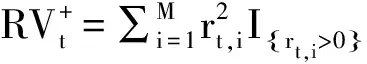
(二)Copula理论模型

Sklar[12]提出的Copula函数是描述变量之间相关性的一个全新概念。其具体定义为，若F为具有边缘分布Fi(i=1，2，…，n)的一个联合分布函数，F与各个边缘分布函数之间的关系可以通过一个称之为Copula的函数C进行描述，即：

F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(11)

(12)

其中，ui=Fi(i=1，2，…，n)。如果F是n阶可微的，则其联合密度函数为：

(13)

(14)

要对Copula函数的参数进行估计，可以对其进行取对数似然函数，然后进行最优化计算，即：

(15)

其中，ξ=(φ1,φ2,…,φn,θ)是包含了边缘分布的参数φi和Copula的参数θ。

如果刻画两个变量之间的相关性，则可以运用二元Copula函数，而常用的二元Copula函数为正态Copula(Norm Copula，N-Copula)和二元t-Copula。Patton[13]依据ARMA(1,10)过程，提出了二元N-Copula和二元t-Copula的相关系数的方程形式：

(16)

(17)

三、经验分析

(一)数据及描述性统计

考虑到“沪港通”于2014年11月17日实施这一背景，为了前后便于对比分析，本文将样本的数据区间定为2013年1月1日至2016年12月31日，即前后大致为两年，共计4年的样本。同时，本文采用的是5分钟高频数据，然而沪港两市交易机制的差别，每天的高频数据量不同。沪市每天上午9:30—11:30，下午13:00—15:00共计4个小时，48个5分钟高频数据，港市每天上午9:30—12:00、下午13:00—16:00共计交易5.5小时，66个5分钟高频数据，为了进行对比分析和Copula建模研究，剔除了两个市场之中独有的交易日期之后共计939个交易日。沪港指数日收益率的描述性统计如表1所示。由表1可知，虽然港市相比沪市而言与正态分布更加接近，如峰度为5.1900，比沪市的峰度8.7135低，其偏度也较沪市更加接近于0，但从正态分布检验的统计值Jarque-Bera可知，两个市场均拒绝服从正态分布的原假设。因而正态分布无法对两市进行准确建模分析。

表1 HS300指数日收益率的描述性统计

注：***、**和*分别表示在1%、5%和10%的水平上显著(下同)，Jarque-Bera为正态分布检验的统计值。

(二)沪港股市的高频波动建模

首先，根据HAR等模型的建模需要，计算RV、RQ、RJ、BPV、R_S_n_d和R_S_p_d序列，具体的计算过程请参阅前文理论部分。沪港股市RV及RQ等序列的描述性统计如表2所示。由表2可知，沪市相较港市，以上各序列均较大，而这些序列具有对每日波动的刻画能力，因此，沪市较港市具有较大的波动。另外，根据Dickey-Fuller单位根检验结果可知，各序列均显示为平稳序列，因而可以对其进一步建模分析，为HAR等长记忆波动率建模奠定了良好的基础。而在滞后24阶的情况下，除了恒生指数RQ之外，沪港其余的RV等序列均显著存在自相关性，因此，运用HAR、HAR-J等具有刻画长记忆能力的相关模型对波动率进行建模具有合理之处。

表2 RV及RQ等序列的描述性统计

注： ADF为Dickey-Fuller单位根检验(下同)。

这里的估计是对整个样本区间，即2013年1月—2016年12月的5分钟高频数据进行样本内建模。表3展示了各模型对RV估计结果的统计分析，由表3可知，HAR、HAR-J、CHAR和SHAR四种模型的估计结果差异不大，沪市波动率的绝对值在24上下，而港市在4上下，由此可知，沪市日内波动大致为港市的6倍。为了便于进一步运用Copula理论分析，这里对各模型的结果进行ADF单位根检验，其结果均显示各序列为平稳序列，因而可以对其进一步采用Copula函数进行建模分析。

表3 各模型对RV估计结果的统计分析

注：这里是各模型所预测的RV扩大了10 000倍后所得出的统计值，极差为最大值减去最小值。

(三)基于Copula模型的动态相关性分析

本文同时采用了二元动态N-Copula和t-Copula两种模型，在进行Copula建模时，笔者采用对应的序列进行拟合，如沪市的HAR序列和港市的HAR序列为一组、沪市的HAR-J和港市的HAR-J为对应的一组，依此类推，四种长记忆模型和日数据，一共考虑了五组数据，即同时对这五组数据运用动态N-Copula和t-Copula进行建模。2013年1月至2016年12月间沪港股市之间运用动态N-Copula和t-Copula具体的估计结果如表4和表5所示。同时，也对日收益率运用Copula进行建模对比分析。

表4 2013年1月至2016年12月动态N-Copula估计结果

注：括号内为参数估计的标准差，L-Likelihood为对数似然函数值，加粗为最小的AIC、BIC对应模型(下同)。

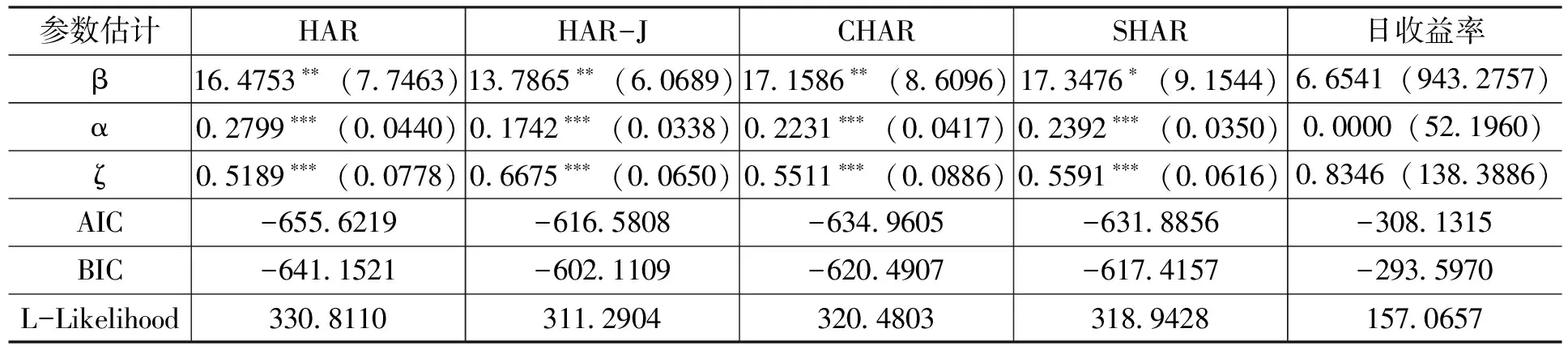
表5 2013年1月至2016年12月动态t-Copula估计结果

从表4和表5可知，在2013—2016年，无论是正态N-Copula还是t-Copula，HAR模型均具有最小的AIC和BIC，因此，可判断基于HAR模型的Copula方法更能够刻画沪港两市之间的相关性。在各种模型下，t-Copula较N-Copula均具有较低的AIC和BIC，由此可以判断动态二元t-Copula较动态二元N-Copula能够更加准确地刻画沪港股市之间的相关性。这是由于刻画t分布自由度的参数均在5%的水平上显著(除SHAR模型在10%水平上显著)，因此，t-Copula充分刻画了两市极端波动之间的相关性。而直接采用日收益率建模的方式对两市之间相关性的刻画能力最弱。

(四)“沪港通”实施前后对比分析

“沪港通”开通前后两市之间的相关性是否具有差别，具有什么样的差别？这是本文拟研究解决的关键问题，下面将继续应用前文的分析方法对此展开分析。由于“沪港通”是2014年11月17日开始实施，为了前后数据对称，本文将从2015年1月1日为中点将样本分为两个子样本区间，即前后各两年时间进行对比分析，以期了解“沪港通”开通之后对两市所带来的影响。

先对各样本区间的5分钟高频数据分布应用HAR、HAR-J、SHAR和CHAR四种模型对沪港两市子样本进行对应建模，并以此估计结果为基础采用动态t-Copula对其相关性进行拟合，表6和表7分别为2013年1月至2014年12月和2015年1月至2016年12月两子样本间动态t-Copula估计结果，由此可以发现，在前半部分HAR模型具有最小的AIC和BIC，但在具有较大波动的后半部分，具有跳跃刻画能力的HAR-J模型显示为最佳模型。与总样本一样，两个子区间中直接采用日收益率建模方式对两市之间相关性的刻画能力最弱。从表6中刻画t-Copula自由度的参数可知，HAR-J和CHAR模型在5%的水平上显著，HAR和SHAR模型在10%水平上显著，而此区间沪港股市均有较大的波动，t-Copula的估计结果表明了两市剧烈波动之间的相互影响。

本文对沪港两市间各模型所估计的动态相关系数的均值进行了统计，具体结果如表7所示。总体而言，HAR、HAR-J、CHAR和SHAR四种模型所估计的动态相关系数差异不大，各个区间其均值差异在3%左右。从2013年1月至2016年12月总样本以及2013年1月至2014年12月和2015年1月至2016年12月两个子样本区间来看，基于日收益率的相关系数则在整个样本期间和两个分样本期间相差不大，但基于高频数据的其他模型则在前后两个不同样本期间具有较大的差异。具体而言，在沪港通开通之后沪港两市之间的相关性较之前有大幅提升，以后半段刻画沪港股市动态相关性最佳的HAR-J模型为例，其前后相差达到了17.10%，表明“沪港通”实施之后两市之间的相关性提升17.10%。其他几个模型所估算的相关性提升幅度同样在12%以上。

表6 动态t-Copula估计结果

表7 各模型动态t-Copula相关系数均值统计结果

注：子区间差异为2015年1月至2016年12月的相关系数均值减2013年1月至2014年12月的相关系数均值。

(五)沪港股市风险传染分析

从上文的经验分析可知，“沪港通”的实施使得两市之间的关联程度大幅提升，相关性提升是来源于沪市对港市的影响增强还是相反？这是本文进一步研究的问题。两个序列之间的因果联系可以通过格兰杰因果检验进行判断。格兰杰因果关系检验要求估计以下回归模型：

(18)

(19)

其中，Xt和Yt为X、Y原始序列当期值；Xt-i、Yt-i为X、Y原始序列滞后i期的值；αi、βi、λi、δi为回归系数；μ1、μ2为误差项。

格兰杰检验是通过构造F值，利用F检验完成的。如针对X不是Y的格兰杰原因这一假设，即针对式中X滞后项前的参数整体为零的假设，分别做包含与不包含X滞后项的回归，记前者的残差平方和为RSSU，后者的残差平方和为RSSR，再计算F值：

F=(RSSR-RSSu)×(N-2n-1)/RSSu×n

(20)

其中，n为X的滞后项的个数，N为样本容量。

如果计算的F值大于给定显著水平α下F分布的响应的临界值Fα(n，N-2n-1)，则拒绝原假设，即认为X是Y的格兰杰原因。

在经验分析之前，本文对沪港股市的日收益率进行了ADF检验，显示为平稳序列，因而在选取滞后2阶情况下，本文对沪港股市各阶段之间收益率的格兰杰因果关系进行了分析。以5%为置信水平，在2015年1月至2016年12月间，格兰杰检验拒绝了“港市不是沪市的格兰杰原因”的原假设，即港市是沪市的格兰杰原因，而其他区间则两市之间显示没有因果关系。这结论进一步说明了，在2014年年末之后，港市与沪市之间的联系进一步增强，且主要是港市对沪市的影响增强所致。

四、结 论

本文利用日内高频交易数据详细探讨了沪港股市之间的相关关系和因果关系。首先，同时利用了能够刻画长记忆的HAR、HAR-J、CHAR及SHAR四种模型对沪港股市的高频波动进行建模，然后在此基础上利用了动态N-Copula和t-Copula模型对沪港股市2013年1月至2016年12月间的相关关系进行分析，同时以2014年11月17日实施的“沪港通”为标志，将样本分为前后各两年两个子样本进行了经验分析。本文的实证结果表明：动态的t-Copula模型较N-Copula模型更能准确刻画沪港股市之间的相关关系；基于HAR及HAR-J模型较CHAR及SHAR模型对沪港股市间的相关关系具有更佳的拟合效果；“沪港通”实施之后两市之间的相关关系提升幅度达到12%以上，且格兰杰因果关系表明港市对沪市的影响逐渐增强。

本文的经验分析利用了日内高频交易信息，较以往文献利用日收益建模研究在利用信息方面更加符合实际，为研究沪港两市间的相互关系提供了新的视角和经验依据。本文研究结果与现实推理高度吻合，且从定量角度估算了沪港股市在“沪港通”实施之后两者间的相关关系和因果关系。本文的研究结果表明，参与沪市的投资者、管理者应重视港市对沪市的重要影响，将港市的相关情况纳入到沪市风险管理的范畴之中，做好应对港市变化所带来的相关风险。