不同温度的双卡尔曼滤波算法电池组SOC估计

何 耀，黄东明，刘新天

（合肥工业大学新能源汽车工程研究院，合肥 230009）

电动汽车的发展已经得到世界各国的普遍重视，动力锂电池组作为电动汽车的心脏，为整个电动汽车的运行提供能源支持，其性能和状态会直接影响电动汽车的续航状态。因此动力锂电池组的发展和各参数的实时检测尤其是电池组的荷电状态SOC（state of charge）估计成为电动汽车发展过程中的一个关键性问题[1]。

目前对于电池SOC常见的估计方法有：安时积分法、开路电压法、神经网络法、数学模型法、卡尔曼滤波法和放电试验法[16]等。安时积分法通过对电池放电电流进行时间积分来估计电池的SOC[2]，开路电压法通过对电池组的端电压进行测量从而实现对SOC的估计，但是这种测量方法需要对电池组进行长时间的静置；神经网络法比较适用于电池组运行过程中的实时SOC估计[3]，需要大量相似的锂电池组参考数据作为训练数据；数学模型法是通过建立数学模型来估计电池组的SOC[4]，但是当环境发生变化时，就需要对模型进行修正，并重新估计SOC；卡尔曼滤波法通过递推迭代的方式实现对电池组SOC的最优化估计[5]。但是其对电池模型的选择较为关键。对于上述方法中存在的问题，蒋炜等提出了一种改进的电池组SOC估计方法[6]，其采用开路电压法估算t0时刻的初始SOC值SOC0，再根据温度、循环次数等参数来修正SOC0，最后结合Ah积分法估计任意t时刻的SOC值；邱纲等在单输入神经网络模型的基础上建立了多输入神经网络模型[7]，能比较明显地减小对电池组SOC估计的误差，但对于神经网络模型，其需要采集所有单体电池的实验数据作为训练数据；Pleet和夏超英在电池状态空间模型上运用卡尔曼滤波算法进行递推去修正SOC估计结果[8]；刘新天等针对锂电池组中各单体的不一致性提出了Vmin模型[9]，从而实现了对电池组SOC的较精确估计。但是上述方法在确定模型各参数时，均未考虑各参数受温度的影响，实际上电动汽车在行驶过程中，温度的变化很明显，其对模型准确性的影响也是不可忽视的[15]。

对于上述SOC估计方法中存在的问题，本文在Vmin模型的基础上，通过对模型中的参数进行分析，并运用统计学的方法拟合各参数与相关影响因素之间的关系，从而对原模型进行改进，得到更加精确的模型。以此为基础，采用双重卡尔曼滤波算法实现了对电池组的状态和时变参数的同时在线估计[10-12]，使电池组的SOC估计精度得到提高。

1 动力锂电池组的Vmin模型

Vmin模型是针对电池组的各单体电池的差异性，根据木桶效应推出的一种由电池组中容量最低的单体电池SOC值来反映整个电池组的SOC值，模型的提出是基于电池组内各单体电池为串联的前提。图1为此模型的电池组等效电路。图中Rn表示第n节单体电池的内阻，Vn表示第n节电池的开路电压，V表示电池组负载电压。

其模型表达式为

图1 电池组等效电路Fig.1 Equivalent circuit of battery pack

式中：SOCn为电池组中第n节电池的SOC值；Vmin为电池组中各单体电池最低的负载电压；Im为电池组m时刻的放电电流；h为电池的开路电压与电池SOC之间的单调函数关系[13]；为电池组中各单体电池的近似内阻。

根据木桶效应的原理，可知电池组SOC为

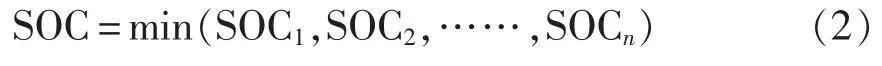
由式（1）和（2）可得

即电池组的SOC值可用组内容量最低的单体电池的SOC值表示。

1.1 模型观测方程

对于式（3）中Vmin的测量可采用Pleet提出的电池模型[14]，其中描述了电池的负载电压与电池充满电的空载电压，电池的内阻、电池的SOC值等因素之间的数学关系，即

式中:Vm为m时刻电池的负载电压；V0为电池充满电的空载电压；Rm为m时刻电池的内阻，其会随着环境因素的变化而变化；k1、k2、k3、k4为与温度有关的系数。

1.2 电池组Vmin的改进

电动汽车在行驶的过程中，遇到的环境会随时变化，其温度差异会非常明显，而在不同的温度下Rm及 k1，k2，k3，k4的实时值都会受到影响，所以需要具体讨论各系数与温度之间的数学关系。

图2给出了3组电池在不同SOC情况下电池内阻的变化情况，显然，电池的内阻随着SOC的增大而有所减小，但是其变化幅度很小。

图3给出了不同温度下电池内阻的变化情况，可见，当温度升高时电池的内阻会逐渐减小；在低温时曲线的变化率较大，说明温度越低，电池内阻受温度变化的影响越加明显。由图2和图3综合可见，温度对电池内阻的影响非常明显，而电池SOC对电池内阻的影响很小。本文将着重考虑各系数与温度之间的关系。

图2 不同SOC时的电池内阻的变化曲线Fig.2 Changing curves of battery internal resistance in different SOCs

图3 不同温度时电池内阻的变化曲线Fig.3 Changing curves of battery internal resistance at different temperatures

根据图3，可以对电池内阻与温度之间的关系进行建模。其模型为

式中：R0为常数项；h1，h2为模型系数；T为温度。

根据实验可得不同温度下的内阻Rm，见表1。

本文运用最小二乘法进行数据拟合，最小二乘法方程为

表1 不同温度下的内阻RmTab.1 Internal resistance Rmat different temperatures

拟合可得模型的各项系数为

1.3 模型观测方程系数 t0，t1，t2，t3 的拟合

结合模型观测方程，在不同温度和SOC条件下进行实验，可以得到不同温度下的系数观察值，如表2所示。再应用最小二乘法进行参数拟合，可以得到各系数与温度之间的数学关系。实验中，通过在-10℃、0℃、10℃、20℃和 30℃的温度环境下对电池放电，并测量相关数据进行分析。

在坐标系中绘出各系数在不同温度下所得的观测值，并且用最小二乘法对点进行拟合，结果如图4～图7所示。

表2 不同温度下系数Tab.2 Coefficient values at different temperatures

图4 t0的拟合曲线Fig.4 Fitting curve of t0

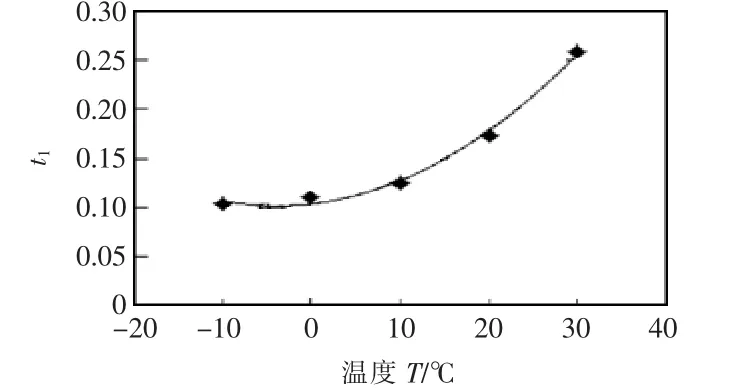
图5 t1的拟合曲线Fig.5 Fitting curve of t1

图6 t2的拟合曲线Fig.6 Fitting curve of t2

图7 t3的拟合曲线Fig.7 Fitting curve of t3

根据曲线的形状，对曲线方程进行建模，其模型为

运用最小二乘法计算得

最后计算得到各方程中所对应系数，如表3所示。表中，R2为决定系数，体现出曲线和实际数据之间的拟合程度，数值越接近于1，其可靠性越高。

表3 各系数的拟合值Tab.3 Fitting value of each coefficient

2 基于Dual EKF的SOC估计

双卡尔曼滤波器Dual EKF（dual extended Kalman filter）是将2个卡尔曼滤波器进行耦合并行工作，同时在线估计系统的状态和时变参数，从而可以提高对电池组SOC的估计精度。

根据Ah积分法可得

式中：SOC为t时刻的SOC瞬时值；SOC0为初始时刻的 SOC 值；ηC为充放电效率；I（t）为充放电过程中任意t时刻的瞬时电流值。

将式（4）和式（9）离散化，可得模型状态方程为

式中，xk+1为k+1时刻系统的状态变量；uk为k时刻系统的电池电流；yk为系统的观测变量；θk为引入的参数向量；f和h分别为由Ah积分法计算SOC的计算公式和单体电池端电压计算公式决定的数学函数；wk、vk为高斯白噪声。在建模时，本文认为新引入的参数向量具有微小扰动，可认为θk+1=θk+rk，rk为噪声干扰。

定义

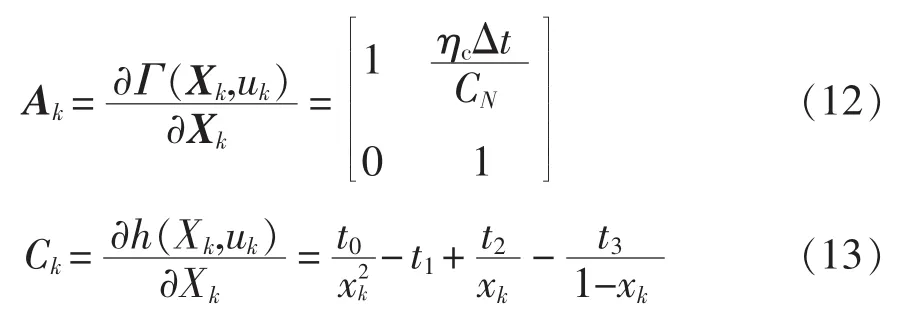
Dual EKF算法估计SOC的步骤如下：

（1）初始化：选取 x0、θ0的初始值；

（2）误差协方差为

（3）时间状态变量更新为

（4）误差协方差更新为

式中：Qw,v为Ah积分法的噪声协方差矩阵。

（5）计算卡尔曼增益为

式中：Qv为电池组端电压估计的协方差矩阵。

（6）系统观测变量的测量更新为

（7）再将更新得到的xk+1和Pk+1代回到第（1）步，重新进行迭代运算就可以得到最有估计值，并且通过2个卡尔曼滤波器的耦合工作，可以较准确地得到系统状态变量和时间变量的实时估计。

3 仿真实验及结果分析

为了验证考虑温度因素之后对锂电池组SOC估计的准确性的影响，选取额定电压240 V，额定容量为20 A·h的电动汽车动力锂电池组作为实验对象。以《电动道路车辆用锂离子蓄电池测试标准》为依据，对整个电池组进行充放电实验。步骤如下。

（1）将电池组充满电（SOC（0）=100%）。

（2）在恒温条件下（30℃±2℃），按照图 8 所示的放电波形进行放电，每个放电阶段先进行电流为60 A的尖峰放电，然后以5 A的恒定电流放电46 min，共放出20%的电量。整个实验过程16 480 s。

（3）静置 30 min，重复步骤（2）4 次。

（4）将温度调整为 10℃和-10℃，再进行 2次实验。

图8 实验中电池组放电电流波形Fig.8 Discharge current waveform of battery pack in the experiment

由于实验只能通过测控机来测量电池组的电流电压，然后应用开路电压法查表得到电池组的SOC值，而本文所提出的改进模型对于电池组的SOC估计，需要结合双重卡尔曼滤波算法、初始值的设定以及各参数的实时更新来估计，并不能直接通过实验得到，所以需要进行仿真得到估计结果。利用上文计算出的参数，在Matlab中建立加入温度因素的电池组SOC估计模型，进行状态向量的初始化，时间状态向量的更新，系统状态的更新，状态向量和时变参数的卡尔曼增益和观测变量的测量更新等步骤。分别以-10℃、10℃、30℃为条件进行仿真实验，将仿真结果与Vmin-EKF法进行比较，结果如图9～图14所示。

图9 -10℃时SOC估计值Fig.9 Estimation value of SOC at-10℃

图10 -10℃时估计误差Fig.10 Estimation error at-10℃

图11 10℃时SOC估计值Fig.11 Estimation value of SOC at 10℃

由图可以看出，在不同的温度下，原来的卡尔曼滤波算法得到的误差较大，而加入温度因素之后再运用双卡尔曼滤波算法对于整个电池组SOC的估计精度能够得到一定程度的提高，两种估计方法在初始时刻的差别并不大，经过时间的推移，差别变得明显起来。主要原因就是双重卡尔曼滤波算法在迭代计算的过程中能够实时在线更新时变参数并且根据实时测得的温度、电压和电流等数据实现电池组状态的实时更新，从而能够更加准确地实现对电池组SOC的估计。本实验选取了3个不同的恒温条件，验证了在不同的温度条件下，加入温度因素后都能够更精确的实现对于SOC的估计，下一步要做的工作就是在温度变化的条件下进行实验，来检测温度时变的情况下是否依然能得到较精确的结果。

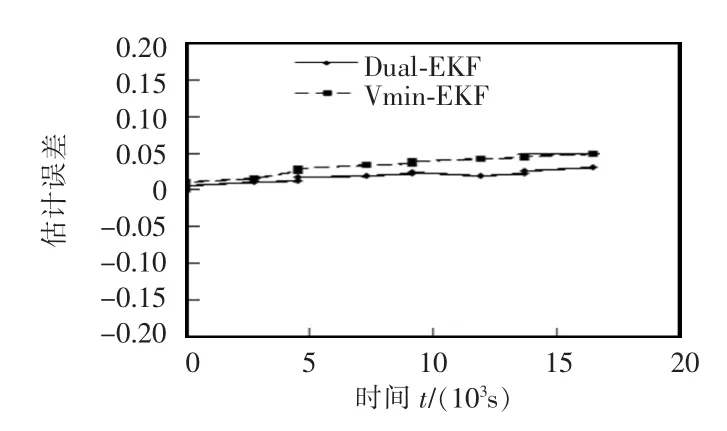
图12 10℃时估计误差Fig.12 Estimation error at 10℃

图13 30℃时SOC估计值Fig.13 Estimation value of SOC at 30℃

图14 30℃时估计误差Fig.14 Estimation error at 30℃

表4为在不同温度下改进Dual-EKF估计方法和EKF方法估计误差的对比，说明了加入温度因素之后SOC的估计精度得到了提高。

表4 不同温度下改进Dual-EKF法与EKF法估计误差对比Tab.4 Comparison of estimation error between the improved Dual-EKF method and the original method at different temperatures

4 结语

本文针对电动汽车锂电池组SOC估计问题中的行驶环境变化大，各单体电池的不一致性，在Vmin模型的基础上，提出考虑温度因素，并进行数据拟合，得出各参数与温度之间的关系，从而使原模型得到改进，以改进的模型为基础，提出用Dual-EKF算法来进行模型的迭代运算，进而实现了系统状态变量和时间变量的实时在线估计。仿真结果表明该方法能够提高电池组的SOC估计精度。后续研究可以考虑电池SOC对电池内阻的影响，让模型更加精确。