利用安培力的冲量公式巧解难题

郑金

(凌源市职教中心 辽宁 朝阳 122500)

将二者联立可得电荷量与磁通量变化量的关系式

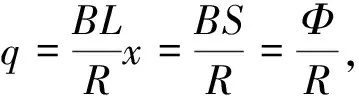
当用“电磁感应笔”的笔尖在特制的书写板上书写时，电池正极、笔尖、书写板、鳄鱼铗通过导线与电池负极形成了通断的电流回路，PVC管中流过通断变化的直线电流，PVC管周围激发出环形变化的磁场，引起绕在磁环上线圈中的磁通量的变化，产生感应电动势和感应电流，使套在PVC管上与线圈连接的LED不断闪亮.

图6 组装完成的“电磁感应笔”

通过“电磁感应笔”还可将奥斯特的“电生磁”，与法拉第的“磁生电”有机地统一起来.实验装置如图7所示.

上述实验过程中还可引导学生进一步观察思考以下内容，为后续学习奠定基础：(1)“电磁感应笔”为何只有书写过程中LED才有闪亮，不书写时不论笔尖接触的是绝缘层还是导通层，LED都不亮；(2)书写时为何与线圈连接的正反向的LED都会闪亮；(3)将实验中的电源直接连接LED，其亮度却很低，而同样的这组电池，在书写的过程中引起线圈上LED的亮度却大为增强，这说明线圈中产生的电的某些方面的性能比原有电池还强.从而有效激发学生的进一步思考，增强学生学习的主动性和积极性.

图7 用“电磁感应笔”“磁生电”和“电生磁”

1 人民教育出版社.普通高中课程标准实验教科书 物理·选修3-2(第2版) .北京:人民教育出版社,2010.2～5

2 熊小兰，黄春如.模拟制作法拉第线圈.物理教师,2017(02):56～57

灵活应用安培力的冲量公式和动量定理解答有关问题，可化繁为简，下面举例分析.

【例1】如图1所示，很长的光滑磁棒竖直固定在水平面上，在它的侧面有均匀向外的辐射状的磁场．磁棒套一个质量均匀的圆形线圈，质量为m，半径为r，电阻为R，线圈所在磁场处的磁感应强度为B．让线圈从磁棒上端由静止释放沿磁棒下落，经一段时间与水平面发生弹性碰撞并反弹，线圈反弹速度减小到零后又沿磁棒下落，这样线圈会不断地与水平面相碰下去，直到停留在水平面上.已知第1次碰后反弹上升的时间为t1，下落的时间为t2，重力加速度为g，不计线圈中电流产生磁场的影响.求：

(1)线圈第1次下落过程中的最大速度vm；

(2)第1次与水平面碰后上升到最高点的过程中通过线圈某一截面的电荷量q；

(3)第2次落地时的速度.

图1 例1题图

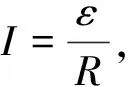
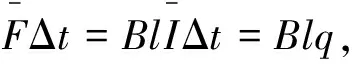
Blq+mgt1=mvm-0

解得

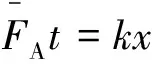
mg(t1+t2)=mv-m(-vm)

可得

v=g(t1+t2)-vm

点评:解题关键是利用微元累加法来求圆形线圈受到安培力的冲量，而且用到了两个安培力的冲量公式.

【例2】(2014年安徽二模)如图2所示，在光滑绝缘水平桌面上，有一直径为L的圆形线圈，空间有竖直向下的有界匀强磁场，宽度为2L，线圈以垂直于磁场边界的初速度v0进入磁场且最终离开.则线圈在进入磁场和离开磁场的过程中，下列说法正确的是( )

A.线圈中产生的感应电流方向相同

B.线圈速度的变化量相同

C.线圈受到的安培力方向相反

D.线圈中产生的热量相等

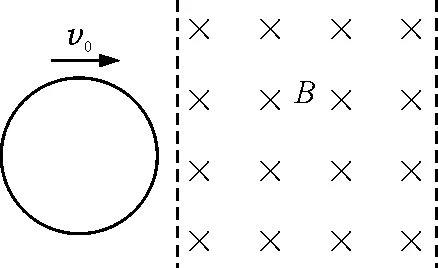
图2 例2题图

解析：由于线圈进入磁场时磁通量增加，离开磁场时磁通量减少，因此感应电流方向相反，选项A错误.线圈先后受到的安培力始终为阻力，则方向相同，选项C错误.

线圈进入磁场过程中，速度较大，电流较大，受到的安培力较大；而线圈离开磁场过程中，速度较小，电流较小，受到的安培力较小.但发生的位移相同，因此两个过程中克服安培力做的功不同，则产生的热量不相等.选项D错误.只有选项B正确.

假设线圈为矩形线圈，左右两边长度为L，由动量定理有

BLq=mv0-mv1

对于线圈穿出磁场过程，由动量定理有

BLq=mv1-mv2

可知两个过程中的动量变化量相同，因此速度变化量相同.

对于圆形线圈，切割磁感线导体的等效长度不断变化，则安培力的冲量Bql是变化的，但在两个过程中的l都是从零增大到L，再减小到零，而Bql中不含有其他变量，只有l一个变量，最小值是零，最大值是L，那么l的平均值不是对位移平均，也不是对时间平均，而是对自己各值取平均，由于线圈在进入磁场和离开磁场的两个过程中，切割磁感线导体的长度变化是一致的，是相同的，则平均值是相同的，因此在两个过程中安培力的冲量相同，所以动量的变化量相同，则速度的变化量相同.故选项B正确.

点评：解题关键是对圆形线圈进入磁场和离开磁场两个过程中受到安培力冲量大小的比较，方法很巧妙.

【例3】如图3所示，一根电阻R=6Ω的导线弯成一根圆形线圈，圆半径r=1m，线圈质量m=0.1kg，此线圈放在绝缘光滑的水平面上.在y轴右侧有垂直于线圈平面的匀强磁场，磁感应强度大小B=0.5T.若线圈以初速度v0=10m/s沿x轴方向滑进磁场，当线圈恰有一半进入磁场时，求此时线圈的瞬时速度以及圆环内产生的焦耳热.

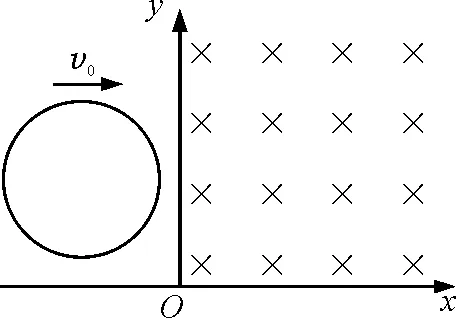
图3 例3题图

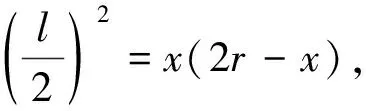
进行积分可得全过程中安培力的冲量

由于l2=4x(2r-x)=-4x2+8rx，则

由动量定理有I=mv0-mv，可得线圈有一半进入磁场时的速度为

由能量守恒定律可知，焦耳热为

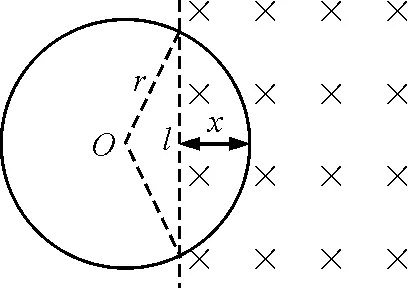
图4 线圈进入磁场x时的示意图

点评:解题关键是对圆形线圈利用微积分来求安培力的冲量，即先用微元法表示安培力的冲量，然后再取积分.由于该题在常规解法中涉及到微积分运算，因此常见一些改编的错题，即在题中给出电荷量或焦耳热的数值，以避免微积分运算，但却容易导致数据不自洽，这是值得注意的.可作出图像如图5所示，利用抛物线与横轴之间面积的结论来计算x=r时对应抛物线与横轴之间的面积.

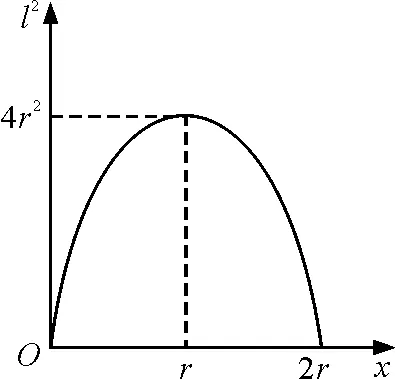
图5 l2-x图像

综上可见，对于某些有关圆形线圈穿越磁场而引发电磁感应的疑难问题，利用安培力的冲量公式和动量定理解答，不仅拓展了思路，而且降低了难度.但在分析安培力的冲量时，要注意圆形线圈在匀强磁场中的等效长度是变化的.