高中数学习题课变式教学的研究探讨

（贵州省独山县民族中学 贵州独山 558200）

一、高中数学习题具有的特点

1.抽象性和概括性比较普遍。相比较其他学科的知识而言，数学知识要比其他学科的更加具有概括性和抽象性，并且概括程度要高出很多，使得概括出来的数学知识仅具有形式的数量关系而完全脱离了具体的实际。所以，在高中数学习题中使用的大都是高度概括和抽象化了的语言。

2.具有很强的严谨性。由于数学本身具有很强的严谨性，因此使得高中数学习题具有很强的严谨性。

3.具有大量的频繁性。由于数学是每天都必须有的必修课程，并且具有很强的实用性，这就使得高中习题也要具有很强的频繁性来巩固学生每天所学的内容。

二、变式教学的定义

对变式的定义研究的人有很多，但大多数人都一致认为变式就是指对象正例的变化，具体的说就是在变式的过程中，保持事物的本质属性不改变，而仅仅改变事物的非本质属性。同样对变式教学研究的人也挺多，本文主要概括为高中数学变式教学就是将所要解决的数学问题通过改变条件、添加背景、联系实际等多种办法变为开放性题目等多种方式对该题进行研究和探讨。

三、浅谈变式教学的几种主要模式

变式教学在高中数学课堂上以多种模式存在，比如有常量和变量相互转化的模式、有条件与结论的变式、有维数升降的变量模式等等。下面详细讲解几个变量模式：

1.常量变式的应用。对某个数学问题解决完后只进行横向变式和纵向变式，则不叫作变式；当将某个问题解决完后，改变其中的某个常数将其形成一个不一样的问题则变式就产生了。这一方法被广大师生所普遍使用，高效且简单，是加强和培养学生学习能力的一大法宝。但是于此同时如果使用不当就会使得问题的本质发生改变造成更多的问题出现，因此使用该方法要谨慎。比如，复习完函数的图像性质后，并分析它与 siny x= 的图像的关系，通常还利用函数等来分析与y=sinx的函数图像性质。并且以上面以上面的题为例来作为变式研究其他的题目就会变得轻松很多。

2.常量与变量进行互相转化的变式及其应用。

常量与变量进行转化主要有两方面，其一是将常量转化为变量，即将原问题当中的常量变换为变量。这一改变如果不改变原问题的问题性质就符合变式性质，是一个成功的改变。但是如果改变了原问题当中的问题性质，就需要寻求解决办法，通常是将若干情形列举并加以解决，然后依次为铺垫并归纳变式到新的问题当中。如此下来解决新的变式问题就轻松了许多。比如，求函数f( x) = x2- 3 x +1在区间[-1 ,4]上的值域，这一例题讲解完之后就可以设计类似更多的变式了 f ( x) = 2 x2- 6 x +1[-1,4],

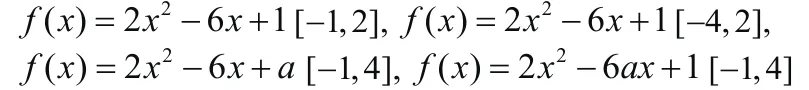
并且，最后一次的变式依赖于前4次的变式，如果没有前面4次的变式，第5次这种概括性很强的变式就比较难发挥其作用。所以，前面的4次变式需要为第5次变式做好铺垫并逐渐过渡到第5次。

3.条件和结论互换的变式。

主要就是指在原问题当中将条件和结论互相置换的变式。

4.设置问题角度不同的变式及其应用。

对同一种材料，如果观察视角不同就会有不同的问题和结论。同样，对同一个图形，如果观察的角度不同也会有不同的问题和不同的结论。比如在讲解立体几何的时候通常可以设置下面的变式方法，来促进对问题的进一步解决能力。在正方体ABCD-A1B1C1D1中，O为AC1的中点，E为CD1的中点，F为BD1的中点，G为AB的中点，H为AC的中点，M为AD的中点，N为CC1的中点.求证：ON平行于上平面，OM平行于右平面，OG平行于前平面，OE平行于上平面，OF平行于下平面EH平行于前平面，FH平行于后平面等类似的问题，只要通过连接各个面的中心，棱的中点以及体的中心三者中的任意两个总能找到某个平行平面。

因此，在同一个图形中，只要不断变化观察的角度就会得出不一样的结论。如此就可以不断地设置新的问题，并引导学生观察、分析和思考问题，培养学生的观察和分析能力，对提高学生的学习兴趣和学习积极性有很大的帮助，这就使得变式教育的精华。并且经过观察证明同一个原理只有经过多次重复学习才能让学生掌握，并且每次的重复学习

对培养学生的观察能力、分析能力、思维能力大有好处；对巩固双基，调动学生学习积极性大有裨益，这正是变式教学的魅力所在。这也正是变式教学的精髓。经验证明同一原理只有多次反复学生才能掌握，并且每次学习不等于简单机械的重复，因为简单的重复学习只能降低学生的学习兴趣，所以这种变式教学要注重对同一种原理、本质和方法的学习，逐渐的变化讲课背景和角度，才能达到变式教学的基本要求。

5.横向变式的方法及其应用。为了建立起各个部分的知识之间的联系，并形成系统完备的知识结构，或者加强学生对某一个知识点的方法的透彻学习就需要采取这种横向变式，使得和原问题处于平行和并列的地位来加宽原问题的应用。如x∈- 则[1,2]

6.横向变式的方法及其应用。为了使学生更好的掌握问题的本质，通常采取递进式的方法层层设计问题，使得问题逐渐深入，引出问题的本质。比如在学生学习数列的时候，可设计如下问题。在数列中，求na，则

总之，变式教学正是在不断的变化问题的背景的同时，使得学生理解原理并牢固掌握方法、规律和问题的本质。