基于DEM数据的地貌类型快速划分系统研究

仲伟敬, 邢立新, 潘 军, 王 婷, 王 凯, 张文哲

(1. 吉林大学 地球探测科学与技术学院, 长春 130026; 2. 西安卫星测控中心 第一活动站, 陕西 渭南 714000)

0 引 言

地貌划分方法很多, 但通常都很复杂, 且人为主观影响较大。DEM(Digital Elevation Model)为地貌学的定量描述提供了丰富的数据支持, 通过DEM数据不仅可以获得高程信息, 还可以派生出许多反应地形地貌特征的地形因子。为了提高地貌提取方法的普适性, 近年来, 不少学者在以DEM数据为基础, 进行地貌分类的方法上取得了一定的进展。此方法以DEM数据为基础, 通过相关算法模型进行一系列操作后, 选取最佳地形因子组合分别实现了对西南、 三峡等地区地貌类型的自动划分, 分类结果较为理想[1-3]。该方法虽然技术相对成熟, 而且可以流程化操作, 但是在实际提取过程中： 部分地形因子不可直接提取, 而且中间步骤过多也使得操作显得异常繁琐。笔者在充分理解相关地形因子模型和相关算法的基础上, 以ENVI(The Environment for Visualizing Images)二次开发平台, 采用IDL(Interactive Data Language)语言, 将流程开发集成, 实现一键化寻找某一地区的最佳地形因子组合, 全(半)自动对地貌信息快速提取。

1 基于DEM的地貌类型快速提取原理

提取流程如图1所示。微观地形因子选取3×3窗口、 采用均值变点分析法分别获得各宏观地形因子的最佳窗口, 将各地形因子采用极差法进行标准化处理, 然后将统一量纲后的地形因子获得相关系数矩阵、 采用雪式熵值法剔除相关系数过大的地形因子, 进而选取最佳地形因子组合。最后采用ENVI中的非监督分类实现地貌信息快速提取。上述过程大致可以概括为最佳窗口下的地形因子获取、 选取最佳地形因子组合和地貌类型自动划分。

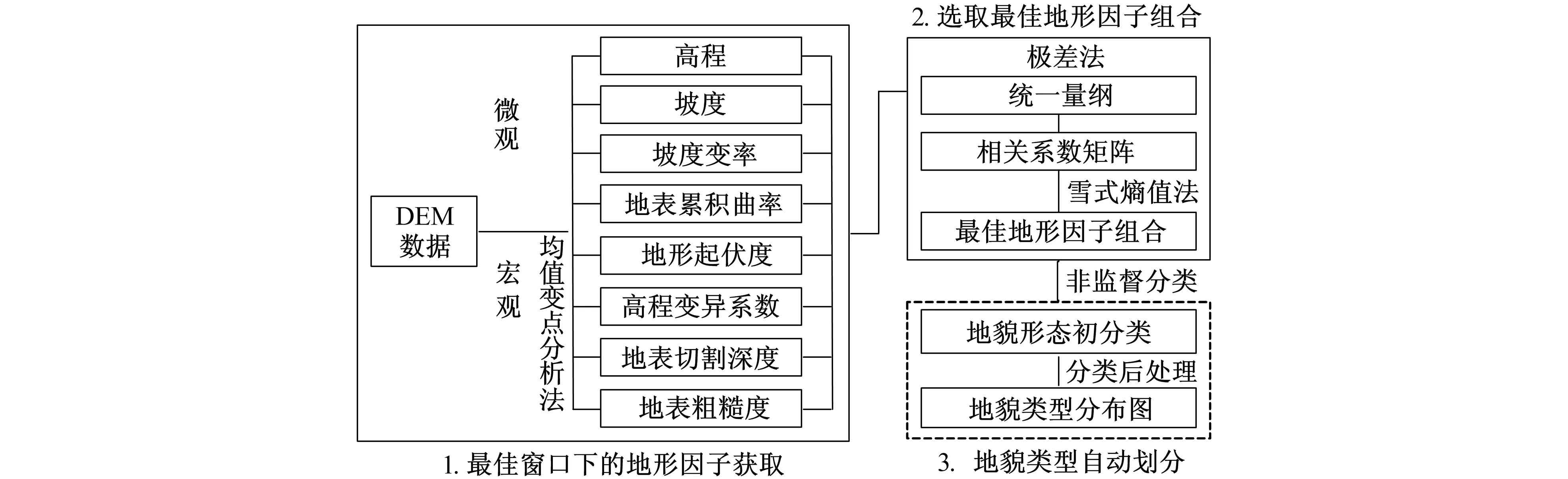
图1 地貌类型快速提取流程图Fig.1 Rapid extraction flow chart of landform types

1.1 相关地形因子概念以及算法

地形因子种类繁多, 笔者结合前人地貌分类经验, 选取高程、 坡度、 坡度变率、 全累积曲率、 地形起伏度、 高程变异系数、 地表切割深度和地表粗糙度8种地形因子[1,2]。其中高程、 坡度、 坡度变率为微观地形因子, 剩余5个为宏观地形因子。地形因子概念以及算法[4]如表1所示。

表1 地形因子概念以及算法

1.2 均值变点分析法确定宏观地形因子最佳窗口

对于微观地形因子, 普适的分析窗口为3×3窗口； 而对于宏观地形因子, 选取最佳分析窗口可以有效提升分类效果, 针对不同区域, 如何确定最佳窗口是宏观地形因子算法模型的关键。笔者选择均值变点分析法确定宏观地形因子的最佳窗口, 并从3×3窗口一直计算到33×33窗口, 步长为2, 以求取地形起伏度的最佳窗口为例, 计算步骤如下[5-7]。

1) 计算序列X

Xi=ln(ti/si)(1)

其中序列X为{Xi,i=3,5,7,…,33}；ti为各窗口下的地形起伏度均值(m)；si为各窗口面积大小(m2)；i为窗口大小。

(2)

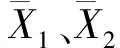
(4)

4) 计算S与Si的差值ΔSi

ΔSi=S-Si(5)

找出ΔSi的最大值, 即为拐点, 对应的i值即为最佳窗口大小。

1.3 极差法统一量纲

由于各地形因子的值域不同, 在实际地貌分类时往往会造成权重不同, 为了消除这种影响, 需要对其统一量纲。笔者采用极差法进行标准化处理, 算法如下[6]

=255(xij-xmin)/(xmax-xmin)(6)

1.4 雪式熵值法选取最佳地形因子组合

在实际地貌分类过程中, 地形因子维度过多可能会造成分类混淆或者分类不理想, 往往只选取几个彼此隔离程度好、 又最具有代表性的地形因子组合参与分类。在求取各地形因子相关系数矩阵后, 某几个地形因子彼此间相关系数较大, 这时采取雪式熵值法确定各地形因子, 算法如下

S=n/2+n/2ln(2n)+1/2ln|Ms|(7)

其中n为选取的因子数；Ms为n×n的方差-协方差矩阵；S为n维数据子集的熵： 行列式值|Ms|越大,S值越大,n维数据子集含的信息越多, 这时n维因子即为最佳地形因子组合。

2 基于DEM的地貌类型快速提取设计与实现

图2 系统流程以及关键步骤图Fig.2 System processes and key step diagrams

2.1 系统设计

按照图1中地貌类型快速提取流程, 系统流程以及关键算法设计如下(见图2)： 1)输入DEM影像后, 通过均值变点分析法确定宏观地形因子的最佳窗口； 2) 根据各地形因子的概念和算法按照最佳窗口大小分别提取最佳窗口下的微观和宏观地形因子； 3) 通过极差法对提取结果进行统一量纲； 4) 取得各地形因子间相关系数矩阵后, 根据雪式熵值法确定最佳地形因子组合； 5) 最后将最佳窗口下而且统一量纲后的8个地形因子、 相关系数矩阵和最佳地形因子组合输出。

2.2 系统实现

系统以ENVI二次开发平台为基础, 采用IDL语言进行开发, 调用IDL函数包、 ENVI二次开发函数接口, 在函数里设置相应的参数, 根据相关算法实现[8-12], 关键技术如下。

1) DEM影像读取。通过读取文件地址来读取影像和投影信息, 部分代码如下。

dem_image=Read_tiff(dem_address,GeoTiff=geoInfor);读取影像存储到dem_image

dem_geo=ENVI_GET_PROJECTION(FID=dem_fid,PIXEL_SIZE=pixel_size);dem_geo存储影像投影信息

2) 均值变点分析法确定宏观地形因子最佳窗口, 根据算法公式, 以地形起伏度为例, 部分代码如下。

tr_Xi=fltarr(16);tr_Xi用来存放序列Xi

FORi=1,16,1 DO BEGIN

tr_Xi[i-1]=ALOG(tr_mean_0[i-1]/(3+(i-1)*2)/(3+(i-1)*2)/8100);先计算各窗口下地表切割深度均值与各窗口面积的比值、 然后将其结果取对数

ENDFOR

tr_X_average=mean(tr_Xi);tr_X_average用来存放序列Xi的算术平均值

tr_X1_average=mean(tr_Xi[0:7]);tr_X1_average用来存放第1段样本的算术平均值

tr_X2_average=mean(tr_Xi[8:15]);tr_X2_average用来存放第2段样本的算术平均值

tr_Si_DS=fltarr(16);tr_Si_DS用来存放序列Xi与总体平均值的离差平方,DS是离差平方的缩写

tr_X1_DS=fltarr(16);tr_X1_DS用来存放序列Xi与第1段平均值的离差平方

tr_X2_DS=fltarr(16);tr_X2_DS用来存放序列Xi与第2段平均值的离差平方

FOR i=1, 16 DO BEGIN

tr_Si_DS[i-1]=(tr_Xi[i-1]-tr_X_average)*(tr_Xi[i-1]-tr_X_average)

tr_X1_DS[i-1]=(tr_Xi[i-1]-tr_X1_average)*(tr_Xi[i-1]-tr_X1_average)

tr_X2_DS[i-1]=(tr_Xi[i-1]-tr_X2_average)*(tr_Xi[i-1]-tr_X2_average)

ENDFOR

tr_S=total(tr_Si_DS);tr_S用来存放序列Xi的离差平方和

tr_Si_DV=fltarr(15);tr_Si_DV用来存储tr_S与各窗口的离差平方和的差值

FOR i=1,15 DO BEGIN

tr_Si_DV[i-1]=tr_S-total(tr_X1_DS[0:i-1])-total(tr_X2_DS[i:15])

ENDFOR

tr_Si_DV_max=max(tr_Si_DV,index);在S与Si的差值中找最大值点并且找到它的索引值

tr_bestwindow_size=(index+1)*2+1;通过索引值来计算最佳窗口大小

3) 地形因子提取。微观地形因子提取： 对于坡度、 坡度变率以及全累积曲率, 根据算法其中间结果可以在ENVI软件的地形模型模块中直接提取。本系统在实现时需要将该功能抽调出使用, 方法是直接调用ENVI二次开发提供的函数包ENVI_DOIT, 此函数包已经把涉及到的算法集成到一个函数里, 只需根据需要设置几个参数即可, 以坡度为例, 提取代码如下。

ENVI_DOIT,‘TOPO_DOIT’,BPTR=[0],DIMS=dims,FID=dem_fid,IN_MEMORY=1,pos=[0],R_FID=slope_fid,PIXEL_SIZE=pixel_size,KERNEL_SIZE=3

slope_image=ENVI_GET_DATA(FID=slope_fid,DIMS=dims,pos=[0])

宏观地形因子提取。对于地形起伏度、 地表切割深度以及高程变异系数, 根据算法首先需要计算得到中间结果： 窗口下高程的最大值、 最小值、 均值和标准差。然后根据相关公式再一次计算, 将计算结果填充到窗口中间的格网, 然后在整幅影像下进行移动、 循环分别填充到窗口中心。以3×3窗口为例, 如图3所示。

以提取地形起伏度为例, 部分代码如下。

tr_image=fltarr(length,width)

n1=tr_bestwindow_size;n1用来存储地形起伏度的最佳窗口

FORi=1,width-n1+1,1 DO BEGIN;外侧行循环

FORj=1,length-n1+1,1 DO BEGIN;里侧列循环, 从第1列开始循环, 步长为1, 设置窗口宽度为n, 当窗口右侧顶到整幅影像最外侧停止, 停止位置为length-n1+1

window_max=max(dem_image[j-1:j+n1-2,i-1:i+n1-2]); 算窗口内的最大值

window_min=min(dem_image[j-1:j+n1-2,i-1:i+n1-2]); 算窗口内的最小值

window_tr=window_max-window_min;算窗口内地形起伏度： 在一个特定区域内, 最高点与最低点高程的差值

tr_image[j+(n1-1)/2-1,i+(n1-1)/2-1]=window_tr;窗口中心点坐标存进地形起伏度数组

ENDFOR

ENDFOR

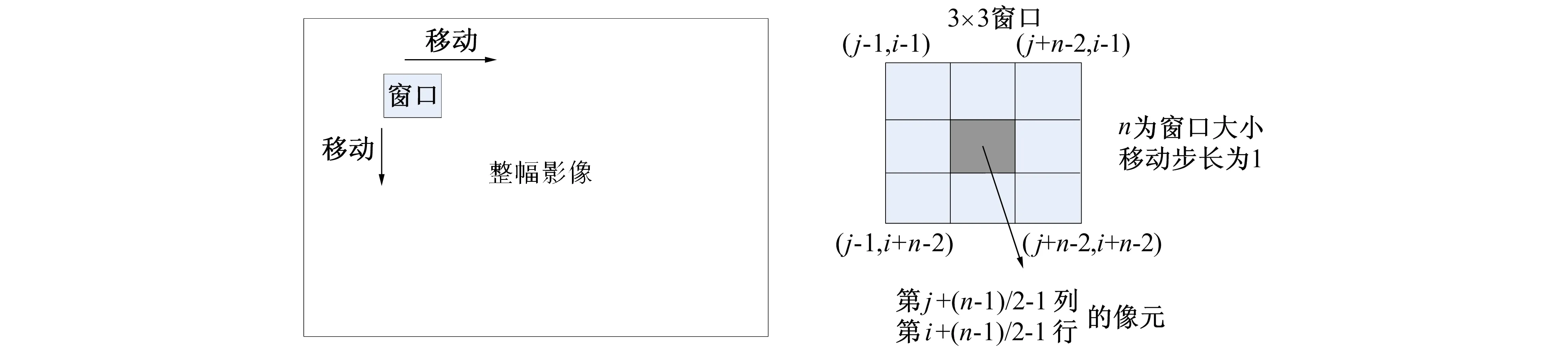
图3 窗口移动示意图Fig.3 Window move diagram

宏观地形因子： 地表粗糙度提取, 先求取不同窗口下的坡度, 然后以坡度为基础根据公式再求取相应窗口下的地表粗糙度, 部分代码如下。

ENVI_DOIT,‘TOPO_DOIT’,BPTR=[0],DIMS=dims,FID=dem_fid,IN_MEMORY=1,pos=[0],R_FID=slope_fid,PIXEL_SIZE=pixel_size,KERNEL_SIZE=33

slope_33=ENVI_GET_DATA(FID=slope_fid,DIMS=dims,pos=[0])

surface_roughness_33=1/cos(slope_33*!DTOR)

surface_roughness_mean_0[(33-3)/2]=mean(surface_roughness_33)

4) 极差法统一量纲, 以高程因子为例, 部分代码如下。

dem_min=min(dem)

dem_max=max(dem)

dem_gui=fltarr(after_n);dem_gui存储归一化后的数据

FORi=1,after_n,1 DO BEGIN

dem_gui[i-1]=(dem[i-1]-dem_min)*255/(dem_max-dem_min)

ENDFOR

5) 相关系数矩阵, 雪式熵值法确定最佳地形因子组合直接调用IDL函数即可, 求矩阵相关系数函数“CORRELATE”、 求方差-协方差矩阵函数“IMSL_COVARIANCES”、 求矩阵行列式值函数“DETERM”, 部分代码如下。

r[i-1,j-1]=CORRELATE(p,q);r为系数

i_c=IMSL_COVARIANCES(all_n1);算方差-协方差矩阵

zhi=DETERM(i_c);算行列式值

6) 结果输出, 以输出坡度变率和不同地形因子组合以及其行列式值为例, 部分代码如下。

write_tiff,‘e: empwork坡度变率3x3窗口.tif’,sv_gui_zhuan,GeoTiff=geoInfor,/FLOAT

openw,lun,‘E: empwork从大到小排列后的地形因子组合以及对应行列式值.txt’,/append,/Get_lun

printf,lun,lian

free_lun,lun

3 应用实例

3.1 研究区以及数据源

长白山位于吉林省东南部, 地处中朝两国的边境线上, 最高峰白头峰2 700 m左右, 研究区以长白山天池景区、 望天鹅景区为中心, 地貌整体形态呈起伏状、 高度逐渐向四周递减, 不同位置相对高程跨度大, 是提取基本地貌类型典型的试验区。笔者数据源选取SRTMDEM数字高程数据产品, 分辨率为90 m×90 m, 精度相当于1 ∶25万DEM, 数据下载自地理空间数据云, 其已经经过一定的数据加工, 根据研究区覆盖范围以及国家线为界限, 将影像裁剪, 地理范围为41°～43°N、 127°～129°E。

3.2 系统快速提取研究区内最佳地形因子组合

将裁剪的DEM影像输入系统后, 不用像以往经过很多步骤、 繁琐操作后得出相应结果, 本系统可一键化先后输出最佳窗口大小下而且归一化后的8个地形因子、 相关系数矩阵以及根据行列式值从大到小排列后的最佳地形因子组合。

1) 宏观地形因子最佳窗口确定：以提取地形起伏度的最佳窗口为例, 如表2所示。在窗口为15×15时ΔSi值最大7.81, 此点即为拐点, 所以地形起伏度的最佳窗口选取为15×15, 面积相当于1.82 km2。其他宏观地形因子最佳窗口提取结果为： 高程变异系数15×15, 地表切割深度15×15, 地表粗糙度13×13。

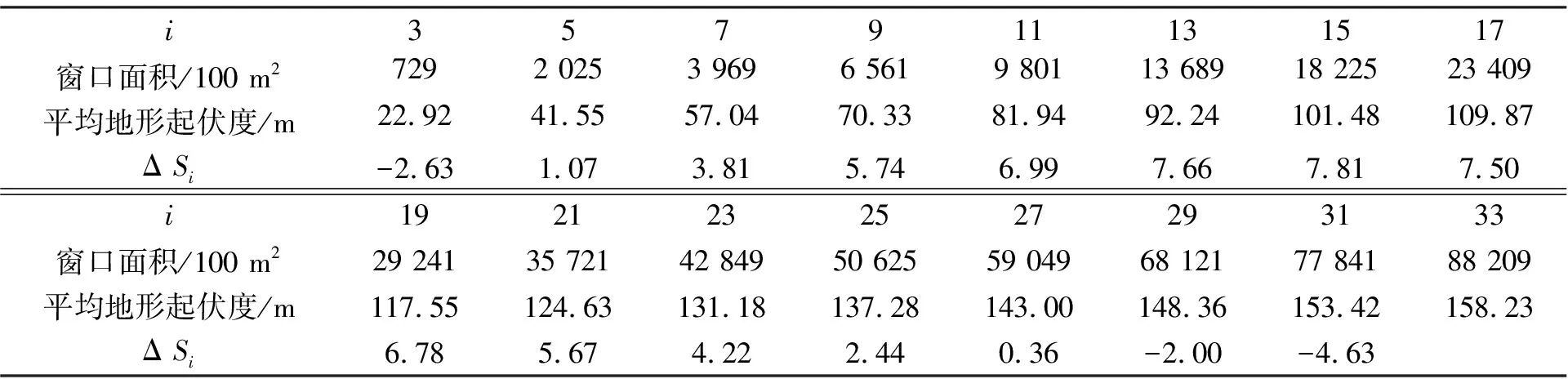
表2 平均地形起伏度与窗口面积对应关系

2) 相关系数矩阵提取结果如表3所示。可看到该研究区内坡度、 地形起伏度、 高程变异系数、 地表切割深度和地表粗糙度这5个地形因子彼此间相关性强, 相关系数均大于0.6。

表3 地形因子间的相关系数矩阵

3) 将归一化后最佳窗口下提取的8个地形因子都输入系统后, 地形因子组合数选取为5, 按照从大到小排列后的方差-协方差行列式值输出结果如表4所示。

表4 不同因子组合的行列式值(已从大到小排列)

其中12 357组合, 行列式值最大, 为最佳地形因子组合； 从序号[1]、[2]、[3]、[4]可看到组合结果分别为12 357、12 367、12 356、12 358： 除1、2、3一样外, 在5、6、7、8中选出两个即可, 侧面印证了2)的提取结果： 即该研究区内坡度、 地形起伏度、 高程变异系数、 地表切割深度和地表粗糙度这5个地形因子彼此间相关性较强； 从序号[54]、[55]、[56]可以看到： 行列式值较小的结果中都有4这个地形因子, 也就是全累积曲率对于该研究区地貌划分最不适用。

综上所述, 选取高程、 坡度、 坡度变率、 地形起伏度和地表切割深度这5个地形因子用于本研究区地貌划分。

3.3 根据最佳地形因子组合对地貌类型全(半)自动划分

起伏度与海拔是区分基本地貌类型的两个重要参数, 长白山最高峰不超过3 500 m, 所以研究区内涉及到的基本地貌类型如表5所示[13,14]。

表5 研究区内基本地貌类型

将系统提取的最佳地形因子组合在ENVI软件下先后进行波段叠合、 非监督分类(ISODAT: Iterative Self-Organizing Data Analysis Technique)和分类后处理即可得到研究区内地貌类型划分图： 1) 波段叠合后如图4所示, 分别以高程、 坡度和地形起伏度作为RGB 3波段假彩色显示； 2) 在非监督分类过程中, 根据长白山区域地貌特征, 将初始分类数目设置为16, 迭代次数设置为15, 循环收敛阈值设置为0.95； 3) 初始分类后逐步进行类别合并/定义、 更改分类颜色、 聚类、 小斑块去除： 在处理过程中会存在图斑(孤岛)现象, 由于生成结果图比例尺为1 ∶20万, 为了统计分析的需要, 在这里图斑过滤窗口取50×50, 得到分类结果如图5所示。

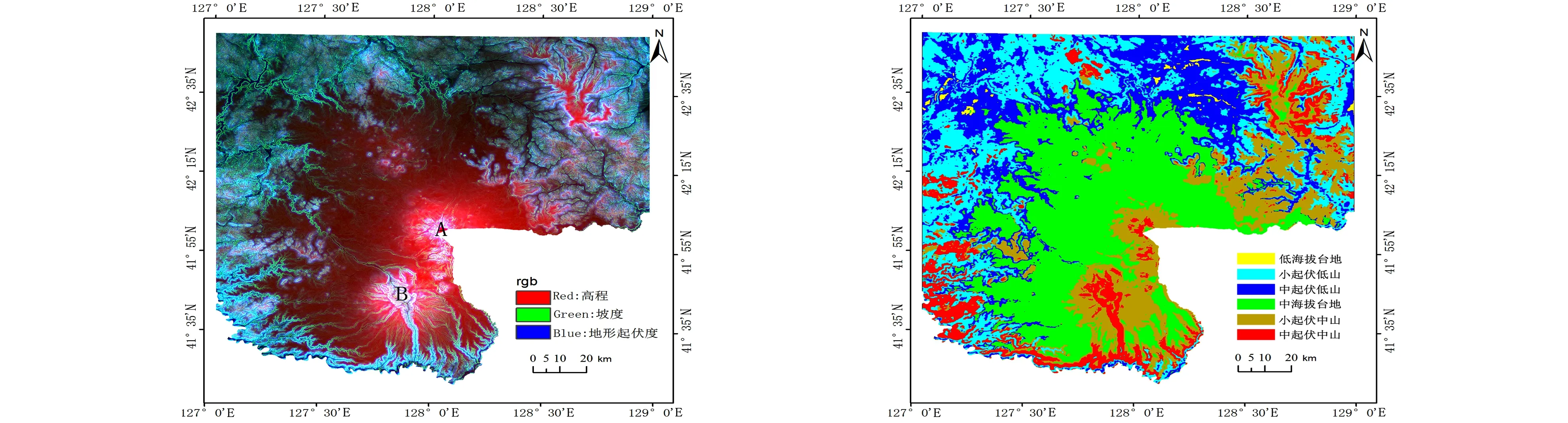
图4 假彩色合成地形因子叠加图 图5 长白山地区地貌类型分布图 Fig.4 False color composite topographic Fig.5 Distribution map of landform types in factor overlay changbaimountain area

3.4 结果分析

前人虽然对长白山地区研究较多, 但尚缺少一个公认的地貌划分结果, 只有1 ∶50万吉林省地貌成图仅供参考。1) 从图4、 图5中可见, 研究区覆盖范围内由左上角逐渐到影像中心海拔逐渐上升； 2) 从图5中可见, 海拔台地占据了绝大部分, 此区域海拔相对较高、 起伏度变化较小, 这与长白山海拔绝大部分处于1 000～1 500 m之间、 坡度一般在10°左右基本吻合； 3) 从图5中也可看出, 低海拔台地分布较少, 这与研究区内平原几乎没有也基本吻合； 4) 从图4中可以看到, A点(天池景区)、 B点(望天鹅景区)变化梯度较大, 这是海拔迅速升高的表现： A点海拔高度在2 200 m, B点海拔在2 050 m左右, 区域海拔呈现快速上升状态, 这在图5中分类结果也有体现。

综上所述, 分类结果相对可靠。

3.5 微观地貌提取

在实际地貌提取过程中, 地貌分类的结果跟数据分辨率有很大关系。笔者又分别选取天池景区和望天鹅景区30 m×30 m DEM数据： 将两个相对较小的研究区DEM数据分别输入系统后, 得到的最佳地形因子组合均为： 高程3×3、 坡度3×3、 坡度变率3×3、 高程变异系数15×15和地表切割深度15×15； 然后将5个地形因子叠合后将研究区分成4类, 得出分类结果, 如图6所示。

a 天池景区实际地物 b 天池景区地貌分类效果图 c 望天鹅景区实际地物 d 望天鹅景区地貌分类效果图图6 实际地物与微观地貌划分对比图Fig.6 Comparison of actual and microscopic features

图6a、 图6c分别是在Google Earth查看的实际地貌： 天池和望天鹅景区； 分类结果图6b、 图6d均未进行任何分类后处理, 图中存在许多斑点, 这里如若对斑点进行聚类、 去除, 其分类结果也是一定程度上的假结果, 所以为便于对结果更好的进行分析, 这里不对分类结果进行任何后续处理。

图6b、 图6d中没有对分类结果进行严格的定义类别, 以图6a、 图6c地图为参考, 无论是山脉、 沟谷还是相对平坦的苔地在图6b、 图6d中都可以清晰的分辨； 但从图6a中也可看出, 天池中心湖水与天池景区四周的苔地化为一类, 所以该方法还需要加入一定的人工影像判别。

4 结 语

利用已有的算法和模型, 借用ENVI二次开发平台、 采用强大的IDL语言编程实现, 可将流程集成化, 使研究人员从繁琐步骤中解脱。笔者结合前人研究成果, 开发了基于DEM数据的最佳地形因子组合地貌类型快速划分系统, 经不断测试, 算法和模型均编写正确, 系统无BUG, 达到了初始的设计要求； 并以长白山作为试验区, 以提取的研究区内最佳地形因子组合进行地貌分类, 宏观地貌和微观地貌提取结果均较为理想。

由微观地貌提取结果, 可以看出该方法还存在一定的误判, 需加入适当的人工影像判读；笔者在对均值变点分析法编程实现过程中, 窗口只计算到33×33, 如果按照1 ∶100万比例尺大范围内地貌制图, 此时宏观地形因子的最佳窗口选取还有待考究, 本论文编程步骤仅供参考。