基于不同单颗磨粒模型的微细磨削力研究

杨军 李志鹏 李伟 任莹晖 周志雄

摘 要：微细磨削技术能够实现硬脆材料复杂结构微小零件的高精高效低成本加工.通过深入分析微细磨削机理，考虑刃角圆弧半径的影响，建立了圆锥、球形、三棱锥、四棱锥等4种单颗磨粒切削力模型；采用VHX1000超景深光学显微镜对Φ0.5 mm、#600微磨棒表面磨粒形状进行观测分析并统计，建立了基于单一磨粒模型和基于综合磨粒模型的微细磨削力模型；在ZCuZn38上进行微细磨削试验，对比研究了微细磨削力理论计算结果与试验结果，并基于理论模型讨论了微细磨削力随工艺参数的变化规律.结果表明，单一磨粒模型微细磨削力与综合磨粒模型微细磨削力均能预测不同工艺条件下的微细磨削力，但综合模型微细磨削力的误差最小；不同磨粒模型计算得出的法向磨削力较为一致，但切向磨削力差异较大.

关键词：微细磨削；单颗磨粒；磨削力；微磨棒；模型

中图分类号：TH16 文献标志码：A

Abstract：Microgrinding technology is able to achieve highprecision， highefficiency and lowcost machining of microparts on hard and brittle materials. Based on the deeply understanding of microgrinding mechanism， the cutting models of single abrasive particles including cone， sphere， triangular pyramid and rectangular pyramid were established， which took the radius of edge arc into account. The abrasive particle shape and distribution of the microgrinding tool with Φ0.5 mm， #600 were observed and counted by ultra depth optical microscope VHX1000. Then the microgrinding force models based on single abrasive particle models and comprehensive abrasive particle model were established. The microgrinding experiment was performed on the ZCuZn38 and the measured microgrinding force was compared with that obtained from microgrinding models. The change of microgrinding force with process parameters was discussed according to the proposed microgrinding force models. The results show that the microgrinding force models based on single type of abrasive particles and different types of abrasive particles can predict the micro grinding force under various process parameters. However， the microgrinding force model based on different types of abrasive particles has minimal error. The normal grinding forces calculated from different single abrasive particle models are close， but the calculated tangential grinding forces are obviously different.

Key words：microgrinding；single abrasive particles；grinding force；microgrinding tool；models

微細磨削是指采用微机床设备、微磨棒（小于1 mm，也称微磨针）磨具针对复杂形状微小零件的机械去除加工方法，是一种能够实现高硬度、高强度硬脆材料微零件或微结构的高质量表面加工工艺[1].采用微细磨削加工技术相比于采用超精密磨床的传统磨削加工不仅在设备成本及能耗上有巨大优势，而且加工方式也更加柔性化.因此，微细磨削技术受到国内外研究人员的广泛关注.但是微细磨削与传统磨削相比不仅仅是简单的设备、工具的缩小，其磨削机理也有很大不同，如在磨粒半径与磨深比值方面，微细磨削工艺（50～100）远大于传统磨削（0.1～1.0）；磨粒几何形状上，微细磨削的磨粒刃角圆弧明显，负前角较一致，而传统磨削中的刃角圆弧几乎可以忽略，负前角变化范围大等.正是由于上述不同，导致在传统磨削中可以忽略的耕犁力在微细磨削中所占比重较大[2]，且磨粒及磨削量的急剧减小导致尺寸效应的影响也更加显著，这就使得传统磨削力模型已难以适用于微细磨削.而磨削力是评价磨削工艺的重要参数，影响到工具的使用寿命、磨削接触区温度、磨削比能、工件表面质量[3]等，因此通过分析微细磨削磨粒切削机理，进而建立微细磨削力模型对于微细磨削技术的研究具有重要的意义.

磨削是多刃切削过程，由于磨粒数量多，几何形状不规则，磨削深度不一致，导致试验、观察、分析磨削过程很困难，因此从单颗磨粒切削入手研究磨削机理，是认识复杂磨削作用，进而建立磨削力模型的重要手段[4].Park等[2]将磨粒简化为球形，假定最小未变形切屑厚度为0.1～0.2倍的切削刃半径，以麦钱特公式和布尔硬度测试为根据，建立了微细磨削的磨削力模型；郝云霞[5]基于概率模型建立了半球形磨粒表面的受力分布函数，得到了微细端面磨削的磨削力模型；赵晶华[6]基于单颗圆锥磨粒建立了超声振动辅助磨削力模型，并应用于聚酯氨橡胶微细沟槽超声振动辅助磨削；Zhao等[7]基于球形磨粒建立磨削力模型，结合试验分析得到了磨削力最小和最大的晶粒取向.综合分析已有研究，可以发现微细磨削力的建模，大多基于球形磨粒，且主要以Park等提出的球形磨粒为基础进行改进；而传统磨削则基于棱锥[8-9]、圆锥磨粒[10-11]的居多，或者直接建立宏观综合磨削力模型[12-13].实际上，磨削力的大小与磨粒几何形状有必然的相关性，如Axinte等[14]通过单颗磨粒的滑擦试验来评估磨粒几何形状对材料去除能力的影响，结果表明不同磨粒几何形状对材料的去除方式，材料表面质量等的影响并不相同；Osipov等[15]通过数学模型（z2+x2=（BpyNp）2）设定磨粒几何外形，结合实际测量分析得出高效磨削不同的工件材料均有其对应的最优切刃几何参数.

本文根据微磨棒磨粒的几何形状，将其归类为圆锥、球形、三棱锥、四棱锥等4种不同的单颗磨粒形式，并主要考虑磨粒刃角圆弧半径影响，建立不同单颗磨粒切削力模型；结合商用化微磨棒磨粒的分布情况，建立微细磨削力模型；经试验验证微细磨削力模型并讨论各因素对微细磨削力的影响.研究结果为微细磨削机理的研究及工艺的优化提供重要参考.

1 微细磨削磨粒切削受力分析

微细磨削采用的刀具主要是微磨棒或微磨针，刀杆直径3～4 mm，刀尖直径小于1 mm，如图1所示.附着在刀尖上的磨粒即使在100 000 r/min的超高转速下线速度依然很小，为避免磨粒过早破损、磨钝或脱落，保证加工表面质量，磨粒的切削深度不宜过大.同时根据最小未变形切屑理论，当磨削深度达到一定值时才会形成切屑，因此磨粒磨削深度又不能过小.为保证高效高质量微细磨削加工，磨粒的切削深度应集中在某个区间内.本文将有效磨粒的切削深度设定为h.

如图1所示，单颗磨粒对工件进行滑擦时包括材料的弹性变形区和塑性变形及切屑变形区.弹性变形区内，其弹性回复高度取决于材料物理特性和磨粒几何外形，其值在亚微米级，而#600及以上磨粒的刃角圆弧高度多在亚微米级.为方便建模，将弹性回复高度与磨粒刃角圆弧高度统一起来，即刃角圆弧高度约等于工件材料的弹性回复高度a0（图1），这一接触区磨粒主要受到材料弹性回复力以及工件与磨粒相对运动的摩擦力.磨粒刃角圆弧接触面以上（a0以上）的接触区域主要使材料发生切屑变形流出，因此这一部分磨粒受到切屑变形反作用力以及切屑流出时的摩擦力.

2 单颗磨粒切削建模

通过对微磨棒表面的磨粒进行观测分析，本文将其简化归类为三棱锥、四棱锥、圆锥、球形等4种磨粒形式，如图3所示.Osipov等[15]指出单颗磨粒的切削深度约为磨粒大小的5%，而在微细磨削中磨粒刃角圆弧半径与磨粒的磨削深度在同一数量级.为此，本文设定磨粒以恒定深度滑擦工件表面，且滑擦深度与刃角圆弧半径相等.结合试验工具参数，选择#600的磨粒工具，其平均磨粒直径大小D≈24 μm，磨粒切削深度h取为磨粒大小的5%，刃角圆弧半径r等于切削深度h.弹性回复高度a0为刃角圆弧面高度（图1），超过刃角圆弧高度部分的材料均以切屑的方式去除.

2.1 圆锥磨粒切削受力模型

传统磨削采用的单颗圆锥磨粒模型多忽略刃角半径的影响及切屑流出时对磨粒接触面的摩擦力，其多以臼井英治的模型为原型，通过改进得到适应不同磨削条件的磨削力模型.微细磨削中磨粒粒度小，易脱落，与工件接触的部分大多有刃角圆弧，且刃角圆弧多出现在磨粒与工件接触底部，而这一部分常常是材料发生弹性变形的接触区（图1）.因此本文所建模型考虑刃角圆弧半径的影响和切屑流出时的摩擦力.

2.1.1 单颗圆锥磨粒所受摩擦力

2.2 球形磨粒切削受力模型

将磨粒简化为球形时不存在切削刃，其切削工件时（图2（b）），磨粒半径与接触弧面半径相同，对于球形磨粒，已有学者[2，5]建立了相关磨削力模型.这些模型主要采用麦钱特公式对磨粒挤压后的工件状态进行描述，并通过传统的二维车削力公式进行改进计算，从而得到单颗球形磨粒三维状态下的磨削力模型.本文在已有的模型基础上对弹性区的摩擦力Ff进行了改进，将球形磨粒受力形式划分为弹性接触区的摩擦力Fbf以及切屑形成力Fbc.

2.2.1 球形磨粒弹性区的摩擦力

2.2.2 球形磨粒切屑形成力

对于切屑变形反作用力和由于切屑流出产生的摩擦力，由于球形磨粒没有切削刃，纯粹依靠挤压使工件材料达到强度极限，进而形成切屑，如图6所示，因此这两种力很难区分.实际上已有模型[2]中的切屑形成力中包含了切屑变形力和切屑流出时的摩擦力.

2.3 三棱锥磨粒切削受力模型

三棱锥的几何形状如图7所示，由于磨粒尖角脆弱，磨粒实际上是带有圆弧尖面的三棱锥.由于磨粒的滑擦方向是随机的，因此单颗三棱锥可以是其棱刃也可以是其侧面进行切削.如果是侧面进行切削，类似于下文的单颗四棱锥面切削，故此处假定其棱边为切削刃，这就在接触棱边上产生应力集中，此处工件材料也最先破坏，并被两个侧前刀面挤压到磨粒两边，进而形成切屑去除.此外，磨粒的底部仍然会有弹性回复存在.

2.4 四棱锥磨粒切削受力模型

四棱锥磨粒的几何形状如图8所示.类似于三棱锥磨粒，由于磨粒尖角脆弱，磨粒顶端实际上带有圆弧面.不同于三棱锥的棱边切削刃假设，此处我们假设其侧面为切削前刀面，如圖3（d）所示.侧面切削使得工件材料受到相对均匀的挤压力，当压力达到材料应力极限时，工件材料剪切断裂，进而形成切屑并沿正前刀面流出.磨粒的底部仍然会有弹性回复存在.

2.4.1 单颗四棱锥磨粒所受摩擦力

类似三棱锥摩擦力建模，四棱锥磨粒及切削过程示意图如图8所示.图8中，θ为四棱锥磨粒负前角；φ为棱边与轴线夹角；S′为磨粒与工件正前刀面挤压面积.四棱锥磨粒由于有棱边，有确定的负前角，因此其刃角圆弧在磨粒底部也不完整，但该圆弧面仍旧是使工件发生弹性变形的主要接触面.磨粒在工作时，在a0深度范围内工件发生弹性变形，并且在磨粒运动时产生切向摩擦力Ftf.

3 微细磨削力建模

微磨棒中埋入基体内的磨刃不会参与磨削，实际参与磨削的磨刃数将少于微磨棒表面的磨刃数，常采用静态有效磨刃数和动态有效磨刃数来衡量.

4 微细磨削力模型的试验验证

为准确统计分析微磨棒表面的磨粒形状及分布情况，本文采用VHX1000超景深光学显微镜对Φ0.5 mm、#600的金刚石微磨棒工作部分进行观测，如图9所示.统计分析结果表明，圆锥形（圆圈）磨粒约占到29.4%，三棱锥形（三角）磨粒约占15.1%，四棱锥形（矩形）磨粒约占26.1%，球形磨粒（圆角矩形）约占29.4%.

本文以ZCuZn38（H62黄铜）为工件（弹性模量E=110 GPa，剪切强度τs=260 MPa），采用OM2A哈斯机床（受试验条件限制，未采用微机床）进行微细磨削加工试验，并采用Kistler 9119AA2测力仪（最小测量值0.002 N）测量微细磨削力，如图10所示.试验得出了不同磨削深度下的微细磨削力，并与基于综合磨粒模型的微细磨削力理论计算结果进行对比，如表1所示.由表1可以看出，理论计算与试验结果在不同磨削深度下其误差大小并不相同，但是都在10.0%的误差范围内，说明本文建立的基于不同形状磨粒的综合磨粒微细磨削力模型能够较为准确地预测微细磨削力.

5 讨论分析

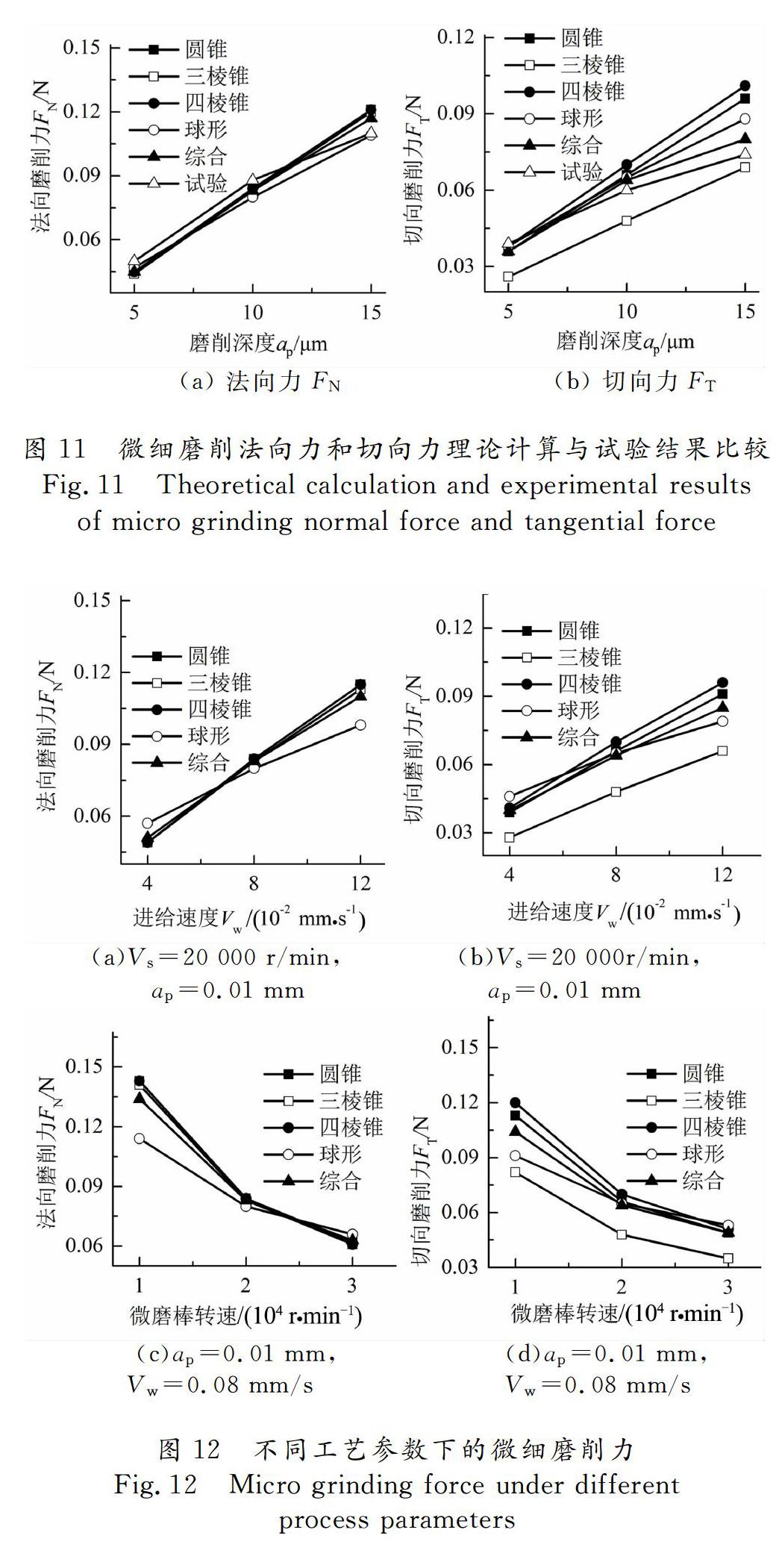
为了进一步分析比较基于单一磨粒模型和基于综合磨粒模型的微细磨削力模型的准确性，本文通过理论计算和试验测量得出了微细磨削力随磨削深度的变化情况，如图11所示.从图11中可看出，不管是基于单一磨粒模型还是基于综合磨粒模型所建立的微细磨削力模型，均能在一定程度上正确地描述微细磨削力随磨削深度的变化规律.但是各个模型的计算结果与试验值相比其误差并不相同，其中基于综合磨粒模型的微细磨削力误差最小，基于球形磨粒模型和圆锥形磨粒模型次之，基于三棱锥形和四棱锥形磨粒模型计算得出的法向磨削力误差较小，切向磨削力误差偏大.可见，仅依靠单一几何形状磨粒模型预测微细磨削力并不够准确，而本文所建立的基于不同形状磨粒的综合磨粒微细磨削力模型能够更加准确地预测微细磨削力.但是，值得注意的是该模型还有一定误差，这是因为在建模过程中忽略了磨削热以及材料应变率随温度、应变速度等的变化；此外，微磨棒变形、磨损及其跳动误差也不容忽视.因此还需要深入研究分析材料的本构模型及微磨棒变形的影响.

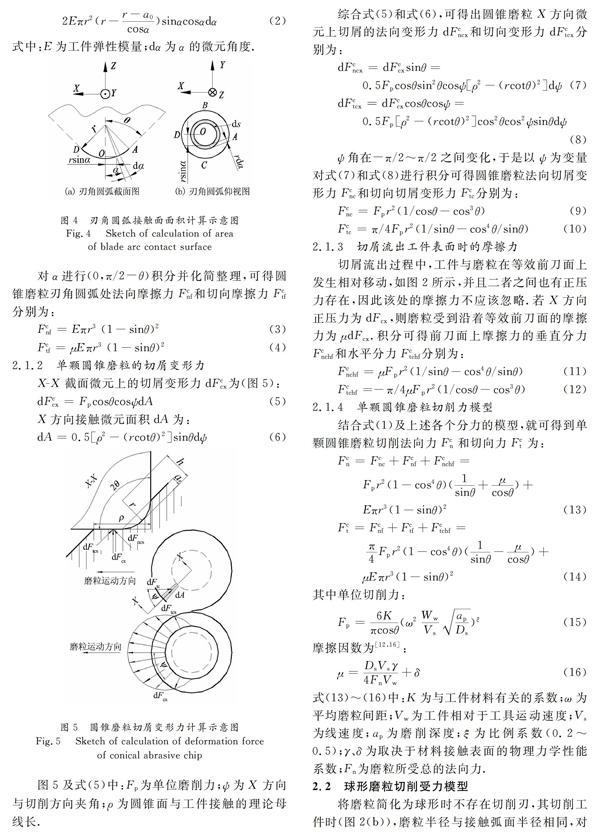
应用本文所建立的微细磨削力模型可进一步得出进给率和转速对微细磨削力的影响规律，如图12所示.从图12可以看出，随着进给速度Vw的增大，切向力和法向力均增大，这是因为进给速度的增大导致磨棒动态有效磨粒数增加，从而导致磨削力增大；而微磨棒转速n增大，却使动态有效磨粒数减少，从而导致切向力和法向力均有所减小；但是随着微磨棒转速的增大，磨削力减小的幅度逐渐减小，说明通过提高磨棒转速来减小磨削力效果有限.此外，不同磨粒几何形状下的法向磨削力较为一致，而切向磨削力的差异较大，其中切向磨削力以四棱锥模型的最大，圆锥模型次之（与综合模型接近），球形模型较小，三棱锥模型的最小.

6 结 论

本文考虑刃角圆弧半径的影响，推导得出了圆锥、球形、三棱锥、四棱锥等4种不同单颗磨粒切削力模型，进而建立了基于单一几何形状磨粒模型和基于不同几何形状磨粒模型的综合磨粒微细磨削力模型，结合微细磨削试验得出如下结论：

1）虽然基于单一形状磨粒模型的微细磨削力与试验相比，均在一定的合理值范围内，但是误差大小并不相同，其中基于球型磨粒和圆锥形磨粒的误差值较小，而基于三棱锥形和四棱锥形磨粒的误差值较大.

2）基于不同几何形状磨粒的综合微细磨削力模型与基于单一形状磨粒的相比，误差值更小，能够更加准确地预测微细磨削力的变化趋势.但是材料特性及微磨棒变形的影响不容忽视，这也是急需攻克的难题.

3）微细磨削力随着磨削深度、进给速度的增大而增大，而随着微磨棒转速的增大有所减小，但通过提高微磨棒转速来减小磨削力效果有限.

4）采用不同几何形状磨粒所得出的法向磨削力较为一致，但切向磨削力差异较大，其中切向磨削力以四棱锥模型最大，圆锥模型次之（与综合模型接近），球形模型较小，三棱锥模型最小.因此仅依靠单一几何形状的磨粒模型来预测微细磨削力并不合理.

参考文献

[1] 李伟，周志雄，尹韶辉，等.微细磨削技术及微磨床设备研究现状分析与探讨[J].机械工程学报，2016，52（17）：10-19.

LI W，ZHOU Z X，YIN S H，et al.Reseaarch status analysis and review of microgrinding technology and microgrinding machines[J].Chinese Journal of Mechanical Engineering，2016，52（17）：10-19.（In Chinese）

[2] PARK H W，LIANG S Y. Force modeling of microgrinding incorporating crystallographic effects[J].International Journal of Machine Tools and Manufacture，2008，48（15）：1658-1667.

[3] 阮日新，羅虎，王永强，等.基于环形磁场励磁的两面磁力抛光试验研究[J].湖南大学学报（自然科学版），2016，43（4）：31-37.

RUAN R X，LUO H，WANG Y Q，et al.Experimental study on double surface maganetic abrasive polishing excited by toroidal magnetic field[J].Journal of Hunan University（Natural Sciences），2016，43（4）：31-37.（In Chinese）

[4] 言兰，姜峰，融亦鸣.基于数值仿真技术的单颗磨粒切削机理[J].机械工程学报，2012，48（11）： 172-182.

YAN L，JIANG F，RONG Y M.Grinding mechanism based on single grain cutting simulation[J].Chinese Journal of Mechanical Engineering，2012，48（11）： 172-182. （In Chinese）

[5] 郝云霞.微细端面磨削机理的试验研究[D]. 沈阳：东北大学机械工程与自动化学院，2009：19-31.

HAO Y X.Experiment study on microend grinding mechanism[D]. Shenyang：School of Mechanical Engineering and Automation，Northeastern University，2009：19-31. （In Chinese）

[6] 赵晶华.聚氨酯橡胶微细沟槽超声振动磨削力研究[D].武汉：武汉理工大学机电工程学院，2012：36-45.

ZHAO J H.Study on the ultrasonic grinding force of microgroove of polyurechane rubber[D].Wuhan：School of Mechanical and Electrical Engineering，Wuhan University of Technology，2012：36-45.（In Chinese）

[7] ZHAO M，JI X，LI B，et al.Investigation on the influence of material crystallographic orientation on grinding force in the microgrinding of singlecrystal copper with single grit[J].The International Journal of Advanced Manufacturing Technology，2017，90（9/12）： 3347-3355.

[8] 余劍武，刘智康，吴耀，等.单颗粒磨削合金钢20CrMo磨削力仿真[J].机械设计与研究，2016（3）：110-113.

YU J W，LIU Z K，WU Y，et al.Simulation research on grinding force of 20CrMo based on single abrasive cutting[J].Machine Design and Research，2016（3）：110-113.（In Chinese）

[9] 余剑武，肖清，罗红，等.单颗CBN磨粒磨削20CrMo的微观成屑过程研究[J].材料导报，2017，31（10）：146-150.

YU J W，XIAO Q，LUO H，et al.Research on micro chip formation process of 20CrMo by single CBN grain grinding[J].Materials Review，2017，31（10）：146-150.（In Chinese）

[10]SUN L，YANG S，YANG L，et al.A new model of grinding forces prediction for machining brittle and hard materials[J].Procedia CIRP，2015，27：192-197.

[11]AZIZI A，MOHAMADYARI M.Modeling and analysis of grinding forces based on the single grit scratch[J].The International Journal of Advanced Manufacturing Technology，2015，78（5/8）：1223-1231.

[12]DURGUMAHANTI U S P，SINGH V，RAO P V.A new model for grinding force prediction and analysis[J].International Journal of Machine Tools and Manufacture，2010，50（3）：231-240.

[13]AGARWAL S，RAO P V.Predictive modeling of force and power based on a new analytical undeformed chip thickness model in ceramic grinding[J].International Journal of Machine Tools and Manufacture，2013，65：68-78.

[14]AXINTE D，BUTLERSMITH P，AKGUN C，et al.On the influence of single grit microgeometry on grinding behavior of ductile and brittle materials[J].International Journal of Machine Tools and Manufacture，2013，74：12-18.

[15]OSIPOV A P，FEDOTOV V V，ZHAROV A A.Experimental study of geometrical parameters of abrasive grains in modeling their cutting edges with the surface of rotation[J].Applied Mechanics and Materials，2015，698：529-533.

[16]TANG J，DU J，CHEN Y.Modeling and experimental study of grinding forces in surface grinding[J].Journal of Materials Processing Technology，2009，209（6）：2847-2854.

[17]任敬心，华定安.磨削原理[M].北京：电子工业出版社，2011：41-61.

REN J X，HUA D A.Principle of grinding[M].Beijing： Publishing House of Electronics Industry，2011：41-61.（In Chinese）