汽车变速器齿轮传动系统动态特性研究及优化

耿智博 肖科 王家序 韩彦峰

摘 要：针对汽车在运行过程中汽车变速器的振动问题，以汽车变速器三挡为研究对象，通过MASTA软件对其进行载荷谱分析，再以提高齿轮的承载能力和尺寸的比值为目标，对三挡啮合齿轮进行优化设计，得到新的模数与螺旋角.综合考虑动态啮合刚度、齿侧间隙、轴承游隙、传递误差的影响建立斜齿轮弯扭耦合的6自由度非线性动力学模型并对传动系统的振动特性进行分析.根据优化前后的振动特性对比，提出了将振动时域信号转化为频域信號进行对比的方法，使得结果更加直观.通过快速傅里叶变换将振动时域信号转化为频域信号.结果表明，优化后齿轮的振动特性有明显的改善，尤其是z向振动减小达到1/4左右.本研究为汽车变速器的振动特性优化提供一定的理论依据.

关键词：汽车变速器；斜齿轮；振动特性；优化设计

中图分类号：TH132.413 文献标志码：A

Abstract：To study the vibration of the automobile transmission， the third gear of the automobile transmission was taken as the investigated subject. MASTA was used to carry out the load spectrum analysis. To optimize the module and helical angle of the third gear， the capacity ratio and the size of the gear transmission system of the third gear were improved. The new modulus and helix angle were obtained by the optimum design. Considering the gear meshing stiffness， backlash， bearing clearance and transmission error， a bendingtorsion coupled nonlinear vibration model with 6degreeoffreedom was established by the lumped mass method. The vibration characteristics were analyzed in detail. In order to compare the vibration characteristics before and after optimization intuitively， a method of translating the timedomain signal into the frequency domain signal was proposed by Fast Fourier Transform. The comparison of the frequency spectrum shows that the vibration characteristics are improved obviously. In particular， the reduction of vibration in z axial reaches about 1/4. It provides a theoretical basis for the vibration optimization of the automobile transmission.

Key words：automobile transmission；helical gear；vibration characteristics；optimization

随着交通的日渐发达，汽车已成为最主要的交通工具，齿轮是汽车传动系统的核心零件，而齿轮传动的振动特性是需要关注的焦点.齿轮传动系统的振动特性受到许多非线性因素的影响，如动态啮合刚度、齿侧间隙、轴承游隙等.所以研究齿轮传动系统的非线性振动已经成为了一个关键问题.

国内外研究人员针对齿轮传动系统的动力学分析做了大量的工作[1-5].Wei等人[6]运用RungeKutta法，研究了齿轮不同重合度、刚度、阻尼以及齿侧间隙等非线性因素对斜齿轮动态传递误差的影响.王奇彬等人[7]考虑直齿轮齿向修形，将轴进行离散化，建立齿轮传动的动力学模型，然后分别用有限元法与其所用方法进行对比，证明了其所用方法能够准确、快速地求解修形后的直齿轮刚度.Wang等人[8]综合考虑了非线性齿侧间隙、静态传递误差、时变啮合刚度等建立了3自由度扭振动力学模型，通过分岔图、相图、Poincaré面、时域响应分析和振幅频率谱分析了不同转速和不同刚度下的齿轮副动态响应.

齿轮的承载能力和尺寸的比值对整个传动系统有着重要的影响.因此，提高齿轮的承载能力和尺寸的比值非常重要[9].所以在保证齿轮力学性能的基础上对齿轮传动系统进行优化就显得格外重要.

许多学者对齿轮传动系统进行科学研究，并通过遗传算法对齿轮系统进行优化处理[10-14].Switonski等人[15]以齿轮传动系统为研究对象，针对齿轮设计参数，适当减小齿轮振动的幅值.Savsani等人[16]以多级传动直齿轮为研究对象，运用优化算法对传动系统设计参数进行优化求解，实现了齿轮的轻量化设计.Daniel等人[17]在考虑传统的模数、齿数和齿宽外，还考虑了两个齿轮的齿廓位移系数，将5个变量一起进行考虑，并将齿轮副体积作为目标函数，以齿根弯曲强度和接触压力为约束条件，采用遗传算法得到齿轮优化的最优值.

以体积为优化目标，同时保证强度是现阶段的常用优化方法[17-19].王成等人[18]以斜齿轮设计和传动要求为约束条件，对齿轮体积进行优化，使得齿轮体积明显减小.宗长富等人[19]在保证斜齿轮强度的前提下以减小传动过程中的冲击振动和齿轮体积为目标，对斜齿轮进行优化，有效降低了斜齿轮的传递误差和体积.

除体积优化外，强度和动态性能优化是另一种途径.刘波[20]运用ANSYS软件构建了船用齿轮箱多体耦合的动力学模型，以减小振动加速度为优化目标，并避开系统固有频率，采用多目标优化理论，运用灵敏度分析确定变量，对齿轮传动系统进行优化.陈克等人[21]针对汽车变速箱齿轮，采用齿向分区的方法对齿轮齿廓进行多目标修形从而降低负载情况下的齿轮振动.周海燕[22]通过对斜齿轮进行参数化建模，提出了从齿轮自身结构参数入手，改善齒轮承载能力，建立了标准斜齿轮的参数化模型.运用ANSYS软件对齿轮的接触特性进行分析，针对齿轮接触载荷分布不均的情况，通过齿向修形的方法进行了改进.王成等人[23]以齿根弯曲应力与齿面接触应力为两个优化目标，对变位系数进行优化，使得齿轮变位系数优化后齿轮副的齿根强度有一定的提高，从而使得齿面接触强度提高.付学中等人[24]考虑了陀螺力矩和齿向偏转力矩等因素，建立单级传动10自由度动力学模型，提出可用于齿廓修形的啮合齿轮刚度模型，并建立了以齿轮传动为基础的齿廓修形动力学优化模型来降低系统的动载系数.

以上文献从较多的方面对齿轮进行优化研究，而针对齿轮的承载能力和尺寸的比值运用MASTA软件进行优化的研究并不多见.本文以汽车变速器三挡斜齿轮为研究对象，分析其载荷谱与动态特性，然后以提高齿轮的承载能力和尺寸的比值为目的，运用MASTA软件进行优化设计，再从振动特性入手，对时域信号进行FFT变换，通过频率谱更加直观地体现出优化后的优越性.

1 变速器模型建立及载荷谱分析

某汽车变速箱中的5个挡位齿轮均为斜齿轮，通过MASTA软件对变速箱建模，变速箱中齿轮传动系统建模后的最终模型如图1所示.

在实际工作过程中，不同挡位所使用时间不相同，而在工作过程中变化的载荷、扭矩与速度之间对应关系就是载荷谱.有了实际工作的载荷谱，就得到了准确的设计输入条件，从而可以得到在载荷谱条件下传动系统中各零件的实际受力情况，获得准确的计算结果.以三挡为例，变速箱的工况如表1所示.

定义模型的输入条件主要根据载荷谱，可以是实际工作情况下的载荷谱和台架试验载荷谱.在MASTA软件中，载荷谱是不同工况的组合，而工况是指某一功率流下作用的转速、转矩及作用时间.根据表1中变速箱的工况定义齿轮传递载荷谱如表2所示.

通过运行载荷谱可以查看功率传递路线并判断其正确性.以三挡为例，图2为三挡位功率谱的传递路线.通过功率谱传递路线可以说明三挡载荷谱正确.选取的齿轮参数如表3所示.

传动系统的承载能力与总体尺寸的比值是评价其设计好坏的重要指标.齿轮是一个传动系统的核心部分，其承载能力和尺寸会对整个传动系统产生重要影响，故提高齿轮的承载能力和尺寸的比值是非常重要的[9].MASTA进行齿轮优化前提是需要保证齿宽、安装中心距以及精度不变，因为在设计过程中很容易使这些参数发生变化.满足上述条件的前提下，以齿轮强度的改进为目标，并在MASTA中选择按照接触安全系数和接触损伤率进行优化.针对压力角、螺旋角和模数3个条件，以三挡为例对齿轮进行优化，优化前后对比如表4所示.

表5为在MASTA软件中进行优化后齿轮的接触安全系数和接触损伤率.

从表5可以看出，优化后的齿轮接触安全系数均有所提高，损伤率均有所下降，说明宏观参数优化可以有效地提高齿轮的强度及其使用寿命.

2 非线性振动模型与方程

2.1 非线性振动模型

运用质量集中法建立汽车变速器动力学模型，作如下假设：

1）忽略摩擦力与系统轴向微动的影响[25]；

2）啮合过程中忽略油膜的影响.

非线性振动模型示意图如图3所示.

3 非线性振动特性分析

以三挡为例，通过求解结果分析该减速器的非线性振动特性.

3.1 振动位移响应

在上述最常见的工况下，该减速器各齿轮各向振动位移响应如图4所示.

由图4可知，各齿轮在y向振动位移均值都在48～50 μm，在z向上的振动位移均值与y向基本相同，但振动幅值只有y向振动幅值的一半左右.各齿轮扭振角位移波动幅度较小，主动轮最大扭振角位移在0.35°左右，从动轮最大扭振角位移接近0.17°，较主动轮有明显的减小.各齿轮振动特性较稳定.

3.2 振动速度响应

在上述最常见的工况下，该减速器各齿轮各向振动速度响应如图5所示.

由图5可知，输入齿轮和输出齿轮振动速度很接近，在y、z向振动速度幅值分别在30 mm/s和20 mm/s附近，y轴方向振动明显比z轴强烈.但主动轮和从动轮扭振角速度相差较大，主动轮约为600 （°）/s，从动轮约为300 （°）/s.

3.3 振动位移速度相图

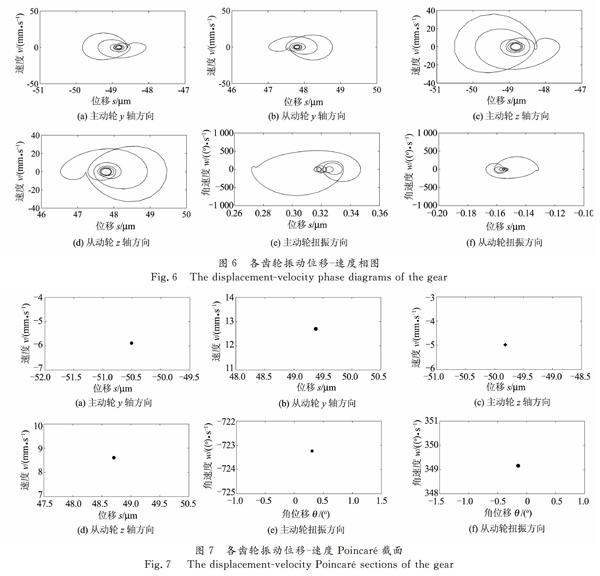
相图是动态系统在相平面上状态轨迹的几何表达.三挡齿轮副传动系统的相图如图6所示.

由图6可知，主动轮与从动轮的相图均为在啮合线处的中心对称图形，并且各齿轮运动相图均为较为简单的封闭曲线，这说明齿轮在做简单的周期性运动.

3.4 振动位移速度Poincaré截面

在非线性动力学研究中，Poincaré截面是一个重要的工具，在Poincaré截面中可定性地观察系统的运动形态.各齿轮振动位移速度的Poincaré截面如图7所示.

由图7可知，三挡齿轮的振动位移速度的Poincaré截面均很简单，说明y、z两个方向都在做较为简单的周期运动，这与上文通过相图的分析结果一致.

3.5 振动加速度响应

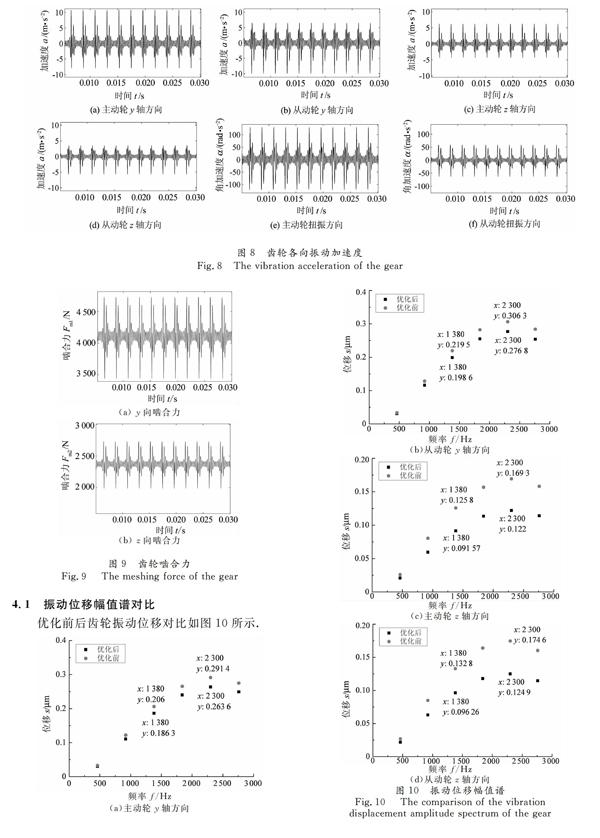
在振动特性分析中，加速度是一项非常重要的指标，通过对振动速度求差分计算，便可以得到振动加速度，如图8所示.

从振动加速度分析图中可以看出，y向的振动加速度幅值明显大于z向，并且主动轮振动加速度明显大于从动轮.单位时间加速度变化频率快直接导致速度波动增大，与振动速度响应分析图中的结论一致.对于扭转角加速度，主动轮的振动加速度在100 rad/s2上下波动，明显大于从动轮的50 rad/s2.

3.6 齿轮弹粘啮合力

得到各齿轮的振动位移后，结合啮合阻尼便可以得到粘性啮合力，再结合引入的非线性因素齿侧间隙便可以得到弹性啮合力.轮齿的动态啮合力为两者之和，啮合力如图9所示.

由图9可知，y向啮合力在4 112.8 N上下波动，z向啮合力在2 374.5 N附近波动，这与通过输入扭矩计算得到的啮合力数值相同.

4 齿轮轮齿优化及仿真分析

为体现优化后齿轮性能的改进，并且使得优化前后的对比更加直观化，对时域振动信号进行快速傅里叶变化（FFT变换），将时域信号转换为频域信号，再将各个频率的幅值进行对比，从而更加直观地得到齿轮传动系统的优化效果，进行更加深入的分析.

由图10可知，振动幅值谱中只有少数的几个波峰，说明斜齿轮副在振动过程中为周期振动，振动具有一定的规律性，随着频率的增加，振动峰值逐渐降低.而在y向振动与z向振动中，均在460 Hz有峰值，且每隔460 Hz就会出现一个峰值，说明y向与z向振动的齿轮啮合角频率具有一致性.以第3和第5个波峰为例，对于主动轮而言，第3个峰值y向振动减小0.02左右，z向振动减小值超过0.03，第5个峰值y向振动减小0.028左右，z向振动减小值超过0.04，优化后的齿轮在y向和z向的振动位移均小于优化前，且z向振动位移减小更为明显，说明MASTA优化后的齿轮振动位移有一定的改进.

4.2 振动速度幅值谱对比

由图11可知，与振动位移相似，在460 Hz以及460 Hz的整数倍处有峰值，这与前文的分析结果具有一致性.同样以第3和第5个波峰为例，对于主动轮而言，第3个峰值y向振动减小0.17左右，z向振动减小值0.3左右，第5个峰值y向振动减小0.4左右，z向振动减小0.7左右，与振动位移类似，MASTA优化后的齿轮振动速度在y向和z向均小于优化前.

4.3 啮合力幅值谱对比

同样以第3和第5个波峰为例，第3个峰值y向振动减小1.95左右，z向振动减小值超过5.1，第5个峰值y向振动减小4.2左右，z向振动减小值超过11.3，在460 Hz以及460 Hz的整数倍处出现峰值.而优化后的齿轮在振动幅值上同样有一定的改善.

4.4 振动加速度幅值谱对比

由图13可知，y向振动加速度明显比z向振动大.加速度幅值谱只有单个峰峰值，系统振动状态相对简单，并且峰值均在460 Hz以及460 Hz的整数倍，与前文分析相符.主动轮第3个峰值y向振动减小0.18左右，z向振动减小值超过0.25，第5个峰值y向振动减小0.4左右，z向振动减小值超过0.56左右，而且优化后齿轮振动加速度同样得到了改善.

5 结 论

1）通过MASTA建立汽车变速器模型，以三挡为例通过功率谱传递来证明载荷谱的正确性.

2）考虑齿侧间隙、轴承游隙、时变啮合刚度等非线性条件，建立三挡斜齿轮弯扭耦合方程，详细分析了斜齿轮的振动位移、振动速度、振动速度位移相图、振动速度位移Poincaré面以及动态啮合力.

3）对齿轮进行参数优化，并对时域振动信号进行FFT变换，转换为频域信号，然后分别比较优化前后齿轮的振动位移、振动速度、振动加速度以及啮合力幅值.在提高齿轮的承载能力和尺寸比值的同时使得传动系统的振动特性得到了较为明显的改善.为汽车变速器振动特性优化提供一定的参考.

参考文献

[1] ERITENEL T，PARKER R G.Threedimensional nonlinear vibration of gear pairs[J].Journal of Sound and Vibration，2012，331 （15）：3628-3648.

[2] 魏静，孙伟，褚衍顺，等.斜齿轮系统分岔与混沌特性及其参数影响研究[J].哈尔滨工程大学学报，2013，34（10）： 1301-1309.

WEI J，SUN W，CHU Y S，et al.Bifurcation and chaotic characteristics of helical gear system and parameter influences[J].Journal of Harbin Engineering University，2013，34（10）： 1301-1309.（In Chinese）

[3] 林腾蛟，何泽银，钟声，等.船用齿轮箱多体动力学仿真及声振耦合分析[J].湖南大学学报（自然科学版），2015，42（2）：22-28.

LIN T J，HE Z Y，ZHONG S，et al.Multibody dynamic simulation and vibroacoustic coupling analysis of gearbox[J].Journal of Hunan University（Natural Sciences），2015，42（2）：22-28.（In Chinese）

[4] 王家序，黄伟，肖科，等.复合齿轮副振动特性仿真及试验研究[J].湖南大学学报（自然科学版），2017，44（2）：40-46.

WANG J X，HUANG W，XIAO K，et al.Numerical and experimental investigation on vibration characteristics of a complex gear pair[J].Journal of Hunan University（Natural Sciences），2017，44（2）：40-46.（In Chinese）

[5] 王旭，伍星，肖正明，等.含裂紋故障的齿轮系统动力学特性研究及其故障特征分析[J].振动与冲击，2017，36（9）： 74-79.

WANG X，WU X，XIAO Z M，et al.Dynamic characteristics of a gear system with crack fault and its fault feature analysis[J].Journal of Vibration and Shock，2017，36（9）： 74-79.（In Chinese）

[6] WEI J，GAO P，HU X L，et al.Effects of dynamic transmission errors and vibration stability in helical gears[J].Journal of Mechanical Science and Technology，2014，28（6）： 2253-2262.

[7] 王奇彬，张义民.齿向修形直齿轮系统动力学特性分析[J].振动工程学报，2016，29（1）： 61-67.

WANG Q B，ZHANG Y M.Dynamic characteristics analysis of a spur gear system with the lead crown relief[J].Journal of Vibration Engineering，2016，29（1）： 61-67.（In Chinese）

[8] WANG J G，HE G Y，ZHANG J，et al.Nonlinear dynamics analysis of the spur gear system for railway locomotive[J].Mechanical Systems and Signal Processing，2017，85： 41-55.

[9] 鄧雷.汽车齿轮变速箱的振动分析与优化设计[D].重庆： 重庆大学机械工程学院，2013： 40-52.

DENG L.Vibration analysis and optimization design of automobile gearbox[D].Chongqing： College of Mechanical Engineering，Chongqing University，2013： 40-52.（In Chinese）

[10]BUTKEWITSC S，STEFFEN J V.A case study on frequency response optimization[J].Journal of Solids and Structures，2001，38 （10/13）： 1737-1748.

[11]王颖，王三民，郭家舜.高速重载齿轮传动多目标优化设计研究[J].机械设计与制造，2012（9）： 7-9.

WANG Y，WANG S M，GUO J S.Research on multiobjective optimization design of highspeed and heavyduty gear transmissions[J].Machinery Design & Manufacture，2012（9）： 7-9.（In Chinese）

[12]DYLEJKO P G，KESSISSOGLOU N J，YAN T，et al.Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J].Journal of Sound and Vibration，2007，300（1/2）： 101-116.

[13]王家序，余波，李俊阳，等.孔销式少齿差行星减速器的多目标优化及动力学仿真分析[J].湖南大学学报（自然科学版），2013，40（12）：50-54.

WANG J X，YU B，LI J Y，et al.The rulti objective optimization and dynamic simulation analysis of hole pin type few teeth difference planetary gear reducer[J].Journal of Hunan University（Natural Sciences），2013，40（12）：50-54.（In Chinese）

[14]付学中，方宗德，侯祥颖，等.变位面齿轮副承载特性分析及变位系数优化[J].华中科技大学学报（自然科学版），2017，45（6）： 57-62.

FU X Z，FANG Z D，HOU X Y，et al.Bearing characteristics and optimal modification coefficient of modified face gear pair[J].Journal of Huazhong University of Science and Technology（Natural Science Edition），2017，45（6）： 57-62.（In Chinese）

[15]SWITONSKI E，MEZYK A.Selection of optimum dynamic features for mechatronic drive systems[J].Automation in Construction，2008，17（3）： 251-256.

[16]SAVSANI V，RAO R V，VAKHARIA D P.Optimal weight design of a train using particle swarm optimization and simulated annealing algorithms[J].Mechanism and Machine Theory，2010，45（3）： 531-541.

[17]DANIEL M， ANTONIO L， DRAGAN ，et al.Influence of profile shift on the spur gear pair optimization[J].Mechanism and Machine Theory，2017（117）：189-197.

[18]王成，沈婷婷.斜齿轮体积优化过程中建模方法的研究[J].燕山大学学报，2015，39（1）：16-21.

WANG C，SHEN T T.Study on volume modeling in process of volume optimization of helical gear[J].Journal of Yanshan University，2015，39（1）：16-21.（In Chinese）

[19]宗长富，任明辉，万滢，等.变速器斜齿轮宏观参数减振优化设计[J].吉林大学学报（工学版），2016，46（6）： 1772-1779.

ZONG C F，REN M H，WAN Y，et al.Optimization of macrogeometric parameters of helical gears of transmissions to reduce vibration[J].Journal of Jilin University（Engineering and Technology Edition），2016，46（6）： 1772-1779.（In Chinese）

[20]劉波.船用齿轮箱动态激励模拟及动力学性能优化[D].重庆： 重庆大学机械工程学院，2015： 42-45.

LIU B.Dynamic excitation simulation and dynamic performance optimization of marine gearbox[D].Chongqing： College of Mechanical Engineering，Chongqing University，2015： 42-45.（In Chinese）

[21]陈克，张津铭.变速箱齿轮的啮合冲击研究与多目标修形[J].中国工程机械学报，2015，13（6）： 504-508.

CHEN K，ZHANG J M.Meshing impact and multitarget modification on transmission gears[J].Chinese Journal of Construction Machinery，2015，13（6）： 504-508.（In Chinese）

[22]周海燕.斜齿轮动力学接触分析及齿向优化研究[D].济南： 山东大学机械工程学院，2015： 56-61.

ZHOU H Y.Dynamics and contact analysis of helical gear tooth optimization[D].Jinan： College of Mechanical Engineering，Shandong University，2015： 56-61.（In Chinese）

[23]王成，刘辉，项昌乐.基于齿轮传动系统横扭摆耦合非线性动力学模型的齿廓修形优化设计[J].振动与冲击，2016，35（1）：141-148.

WANG C，LIU H，XIANG C L.Optimal profile modification for spur gear systems based on their lateraltorsional rocking coupled nonlinear dynamic model[J].Journal of Vibration and Shock，2016，35（1）：141-148.（In Chinese）

[24]付学中，方宗德，侯祥颖，等.变位面齿轮副承载特性分析及变位系数优化[J].华中科技大学学报（自然科学版），2017，45（6）： 57-62.

FU X Z，FANG Z D，HOU X Y，et al.Bearing characteristics and optimal modification coefficient of modified face gear pair[J].Journal of Huazhong University of Science and Technology（Natural Science Edition），2017，45（6）： 57-62.（In Chinese）

[25]黄超.少齿差行星减速器动态特性及非线性振动研究[D].重庆： 重庆大学机械工程学院，2013： 49-51.

HUANG C.Dynamic characteristics analysis and nonlinear vibration research on a planetary reducer with small tooth number difference[D].Chongqing： College of Mechanical Engineering，Chongqing University，2013： 49-51.（In Chinese）