基于专家PID控制和卡尔曼滤波的恒压进样系统

李 路，齐 同，郜晩蕾，王晓冬，贾春平，赵建龙

（1.中国科学院上海微系统与信息技术研究所传感技术联合国家重点实验室，上海200050；2.中国科学院大学北京100049）

微流控芯片使用微机电加工技术在几平方厘米的基片上集成微坝、微阀、微孔膜、微过滤管道等微结构，在药物筛选、细胞检测等方面有着广泛的应用[1]。其中，微流控芯片中微流体驱动技术对实验结果起着关键作用，而微流体的驱动主要采用精密气压控制系统。

目前气压控制系统分为定容积控制和变容积控制[2-5]。采用定容积气压控制系统需要同时采用正压源和负压源控制被控容腔内的压力，使控制系统过于复杂，难以实际应用。而变容积系统具有结构简单，适用性强等特点，并且在做定点压力控制时能够实现比较好的精度和稳定性。国内外学者基于变容积气压控制系统进行了一些研究。例如文献[6]提出一种基于PID算法的变容积控制方案，但由于系统的非线性，采用普通的PID时系统超调大并且调节时间长。目前高精度的气压控制系统往往存在体积大、响应时间长等问题，而针对微流控芯片的进样及检测过程，市场上缺乏相应的自动检测系统，因此本文提出一种新型的基于专家PID控制和卡尔曼滤波的恒压控制系统，并搭建自动化平台，实现微流控芯片的自动进样。

1 恒压进样系统工作原理

本研究设计的恒压进样系统示意图如图1所示。系统主要由柱塞泵、步进电机、电磁阀、压力检测单元、清洗装置、进样针和微流控芯片等组成。步进电机转动的角度与脉冲数呈正比、具有很好的定位精度，并且具有运动的可重复性高、没有累计误差等优点。本系统的工作原理为：首先进样针和微流控芯片入口贴紧实现密封，柱塞泵迅速压缩空气使微流控芯片的进样口和出样口产生压力差。此时应用专家PID控制和卡尔曼滤波算法对压力差进行闭环控制，维持压力差恒定，从而实现微流控芯片的恒压进样。在整个系统中，试剂从进样针流入微流控芯片使气缸内部压力减小，活塞向前运动使气缸内部压力增大，当系统内部压力恒定时，进样针内部试剂减少的体积等于柱塞泵活塞向前移动的体积。因此在恒定压力下，通过步进电机控制活塞的位置实现精确控制体积。

图1 恒压进样系统原理示意图

2 系统建模与仿真

2.1 系统模型

为了验证方案的可行性，首先对整个系统进行建模和仿真。在微流控芯片中，一般认为由于流体的粘性作用力超过惯性作用力使得微流控芯片通道中流体的运动处于层流状态，判断流体是否处于层流状态可以通过雷诺数判断[7]，雷诺数Re定义为：

其中，ρ表示液体的密度，v表示流体的速度，μ是流体的粘度，D表示管道的水力直径，定义为4倍的浸润面积除以浸润周长。本实验中使用的微流控芯片管道的水力直径为18.46 um，去离子水的密度为1.0×103kg/m3，在22℃时水的粘度约为9.6×10-4Pa·s，根据实验优化的流速为10 mL/h[8]，计算得雷诺数为44.5，一般认为雷诺数小于2000时，流体呈层流状态，此时微流控管道中流体的流动满足Poiseuille定律，则流速与压力差呈正比[9]。通过实际测量得到微流控芯片的流速与压力差之间的关系，拟合数据得到微流控芯片的模型为：

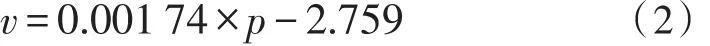
其中，p表示微流控芯片进样口和出样口之间的压力差，v表示试剂进入到微流控芯片的速度。

柱塞泵中的气体可以认为基本符合理想气体状态方程：

式中，n表示物质的量，V表示密闭容器的体积，P表示密闭容器内的压强，R表示理想气体常数。T为密闭容器内的温度。在恒定压力进样过程中，温度可以认为是恒定的。因此密闭容器内部的压力与体积成反比。则系统在t时刻的平衡方程为：

其中，P0为密闭容器内初始压力，V0为初始体积，P（t）为t时刻密闭容器内的压力，v1(t)为活塞移动的速度，v2(t)为试剂从微流控芯片流出的速度。

对式（4）整理得：

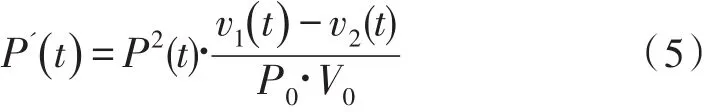
该式描述了密闭容器内压力与活塞移动的速度、试剂从微流控芯片流出的速度之间的关系。由于整个系统是一个时滞系统，采用常规PID控制算法时，容易引起较大的超调量，使系统不稳定，因此本文采用基于专家PID控制和卡尔曼滤波算法实现密闭容器内的压力恒定，并通过MATLAB建模仿真对算法的参数进行优化，然后通过实验验证并与常规PID控制算法的结果对比。

2.2 卡尔曼滤波

要实现恒压过程首先必须获得可靠的气压数据。由气体压力传感器直接测量得到的数据伴随有比较大的测量噪声。因此，首先通过Kalman滤波算法获得可靠的气体压力数据。

Kalman滤波算法的计算方式是采用时域上的递推估计法，计算过程包含预测和更新两个阶段，预测阶段根据前一时刻的预测值估算现在的状态；更新阶段是通过前一时刻的预测值和现在时刻的观测值确定当前时刻的状态估值[10-12]。

系统状态方程为：

其中：A——状态转移矩阵，由于系统的气体压力不随时间变化，取A=1

B——控制矩阵，系统处于恒压状态，可以认为没有控制输入，所以U=0

W——过程激励噪声，其协方差矩阵为Q：

系统的测量方程为：

其中：C——测量矩阵，包含噪声的观测值是状态变量的直接体现，所以C=1。

V——利用气体压力传感器测量气压时的测量噪声，其协方差矩阵为R。

假设系统的初始气压为p0，估计值的方差为P0，则：

时间更新方程为：

其中，Xk-1为k-1时刻气压的预测值，为k时刻的气压估计值。Pk-1为k-1时刻气压的后验估计的协方差。为k时刻气压的先验估计。通过上述两个公式，将气压的状态估计和协方差估计从k-1时刻向前推算到k时刻。

状态更新方程为：

其中，测量更新方程首先计算卡尔曼增益Kk，然后根据气压的测量值Zk计算气压的后验估计。最后根据公式计算气压后验估计的后验协方差。

2.3 卡尔曼滤波效果的验证

经过MATLAB整定后卡尔曼滤波器的参数q=0.001，r=0.05，p=3。为了验证设计的卡尔曼滤波器的滤波效果，在搭建好的恒压控制系统上通过压力传感器采集一组数据，并将滤波前后的数据进行对比。图2为卡尔曼滤波前后对比图，滤波前气压的标准差为2.15，滤波后标准差为1.52，滤波后气压值比滤波前更稳定。

图2 卡尔曼滤波前后对比图

2.4 专家PID控制系统

在控制系统中，最常用的控制规律是PID控制。积分分离式PID控制算法如下：

其中，Kp为比例系数，Ki为积分系数，Kd为微分系数，T为采样时间，β为积分项的开关系数，e（k）为设定值与实际值的差。

针对具有滞后性、被控对象参数不确定、非线性的系统，用常规的PID控制会有比较大的超调量或者调节时间长等问题。专家PID控制是在常规PID控制的基础上根据专家及有经验的操作人员的实际经验，针对具有滞后性、时变、非线性系统等提出的控制方法[13-15]。专家PID控制利用专家系统知识库中的规则推理在线调整PID的参数，既有Bang-Bang控制的快速性，又具有一定的稳定性和抗干扰能力。控制原理图如图3所示。

图3 专家PID控制系统原理图

专家控制器主要包括控制规则集、知识库、推理机和特征识别等[16]。知识库主要包括和压力调节相关的各种数据和经验。控制规则集是专家PID控制器的核心内容，里面主要包括根据专家经验建立的控制气压的规则。推理机主要是根据实时压力变化规律从知识库和控制规则集中选择匹配的规则推理出实际的输出值。

根据现场控制压力的经验，对密闭容器内压力的变化规律进行总结，得到最佳的专家控制规则集。其主要是根据气压变化的误差和误差变化乘积来调整PID的参数。令e(k)、e(k-1)和e(k-2)分别表示当前时刻、前一时刻和前两个时刻的气压误差值。表示当前时刻的误差变化率表示前一时刻的误差变化率。则控制规则为：

1）当|e(k)|＞M1时，说明误差很大，此时采用开环控制，按照最大或最小输出，使误差迅速减小。

2）当e(k)·∆e(k)＞0 且 |e(k)|＞M2时，说明误差较大，且实际气压变化偏离目标值，令β等于0，Kp增大，此时相当于PD控制，使误差快速减小并防止积分饱和。

3）当e(k)·∆e(k)＞0 且 |e(k)|≤M2时，说明误差较小，且实际气压变化朝向目标值，令β等于1，Kp不变，使气压逐步稳定到目标值。

4） 当e(k)·∆e(k)＜0 且 ∆e(k)·∆e(k-1)＞0 或，说明实际气压向目标值变化或者没有误差。此时令β等于1，Kp不变。

5）当e(k)·∆e(k)＜0，∆e(k)·∆e(k-1)＜0且|e(k)|＞M2，说明误差较大且处于极值状态。此时令β等于0，Kp增大，应用较强的控制作用。

6）当e(k)·∆e(k)＜0，∆e(k)·∆e(k-1)＜0且|e(k)|≤M2，说明误差较小且处于极值状态。此时令β等于1，Kp减小。

7）当|e(k)|≤M3时，说明误差很小，此时应用普通的PID控制，使气压稳定在目标值。

以上各式中，M1、M2和M3为设置的误差界限，M1＞M2＞M3＞0。上述的控制规则集就是通过对误差进行特征识别，然后通过专家系统优化PID控制器的参数，实现最优的输出，使控制系统能够针对时变、非线性、系统参数易发生变化的受控对象给出有效的控制策略。

2.5 恒压控制系统仿真验证

为了验证专家PID控制器和卡尔曼滤波算法实现恒压的可行性，本文使用MATLAB的simulink仿真工具对其进行仿真。并根据仿真得到的阶跃响应曲线来判断系统的稳定性。实验中，使微流控芯片的进样口和出样口的压力差突然增加2000Pa，观察系统的阶跃响应。图4为构建的simulink仿真图。

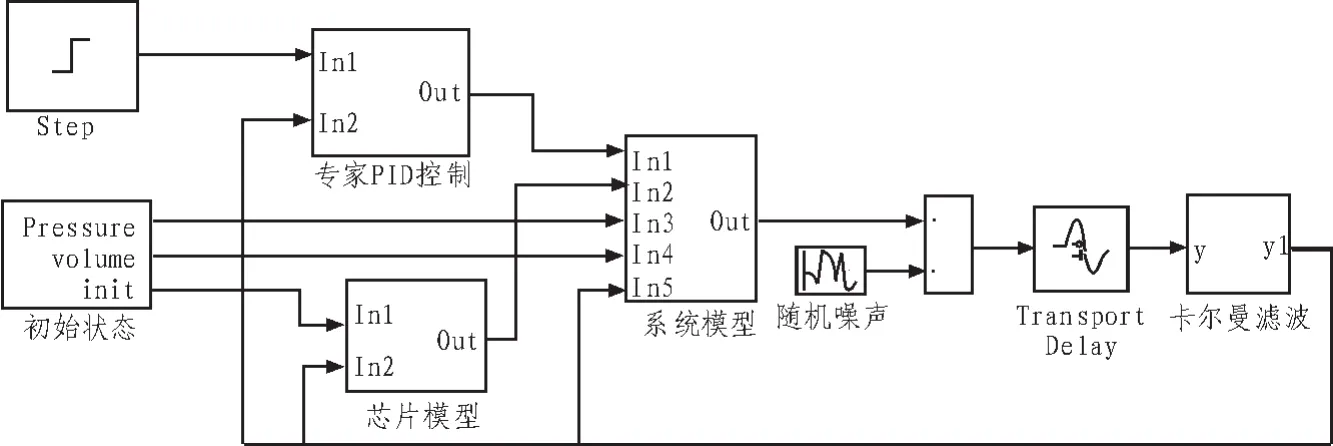
图4 simulink仿真原理图

仿真结果如图5所示，可以看到基于专家PID控制和卡尔曼滤波的控制方案无超调量，响应迅速，在10 s左右即完成调整。

3 恒压控制系统实验验证

图5 simulink仿真结果

图6 微流控芯片自动检测系统

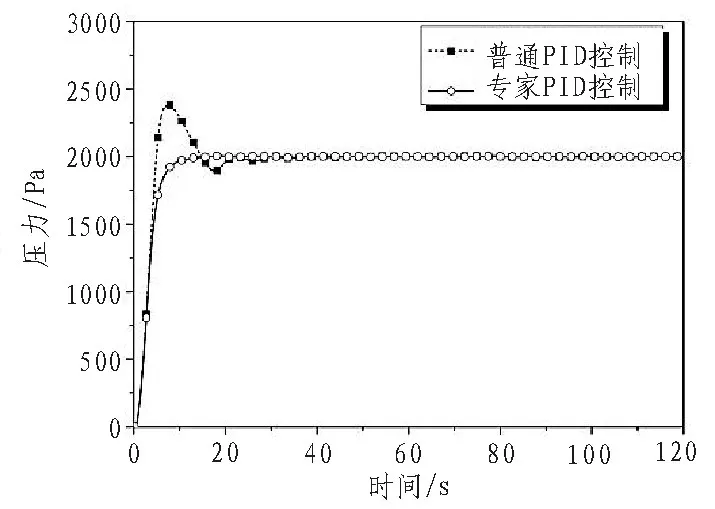
图7 实际测量阶跃响应曲线

根据恒压进样系统的原理，将柱塞泵、压力传感器、微流控芯片、电磁阀及其他连接部件组合起来，图6为搭建好的微流控芯片自动检测系统。硬件电路采用mega2560作为主控制器，压力传感器型号为带有24位∆-Σ型ADC的MS5803-05BA。主控制器采集到压力数据后通过RS232串口将数据发送到上位机保存数据。通过MATLAB仿真和实测修正专家PID的初始值为kp=0.25，ki=0.05，kd=0.02。图7为实际测量的阶跃响应曲线。可以得出由于系统的非线性和迟滞，采用普通PID控制器的超调量为19.2%，响应时间大概为20 s。而专家PID系统无超调，响应时间大概为10 s，响应时间提高了50%。可见专家PID控制系统比普通的PID控制器具有更好的控制效果。稳定后的压力精度为±30 Pa，文献中[6]实现的压力控制精度为±150 Pa，可见本实验方案能够实现更好的效果。专家PID系统通过辨识被控对象的动态特性，结合专家经验，实时调整参数，使控制器始终工作在最佳值上。

为了验证进样系统控制进样试剂体积的准确性，用精度为0.001 g的分析天平（MS105DU，METTLER TOLEDO）称量从微流控芯片出样口流出的水的质量，根据水的密度计算出体积。实验结果如图8所示，压力条件为11400 Pa，温度为室温。在进样体积从20 μL到400 μL范围内，体积控制误差在±10μL以内，决定系数为0.999，说明该系统能够精确控制进样试剂的体积。

4 结束语

为了解决微流控芯片进样时的精确压力控制和微小体积控制问题，实现微流控芯片的自动化进样，本论文提出了一种基于专家PID控制和卡尔曼滤波的恒压进样系统，经过MATLAB仿真和实际测试表明，滤波后压力精度控制在±30 Pa以内，响应时间为10 s左右，进样体积精度为±10 μL，相对于普通的PID控制，专家PID控制具有更好的动态响应。本实验方法便于在嵌入式微处理器中实现，具有易于集成、小型化等优点，为微流控芯片的自动化进样提供了参考。

图8 目标体积与实际测量体积关系图