读懂教材是小学数学有效教学的基础
□文/重庆市南岸区天台岗小学 邹冰秋
《数学课程标准》(2011年版)指出:“数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构,是实现数学课程目标、实施数学教学的重要资源。”也就是说教材是最基本而又最重要的课程资源,是教学内容的重要载体,它凝聚了众多编者对数学教育的认识和对数学的理解,是教师教学和学生学习的蓝本和依据。那么作为数学教师应如何用好这一重要的教学资源呢?笔者认为应读懂数学教材,这是小学数学有效教学的基础。教师应读教材的什么内容?怎样读懂?笔者记为可以从以下几方面入手。
一、读懂教材知识点的编排体系
小学数学知识分为四大领域:数与代数、图形与几何、统计与概率、实践与综合运用。各领域有哪些具体内容,这些内容是如何分布的?这就要求教师既要由上至下的整体了解,又要由下至上的深入分析。即读懂:小学数学知识体系→年段知识体系→单元知识体系→每课时知识点。
读懂小学数学知识体系也就是教师要弄清楚各领域有哪些知识?这些知识在整个小学阶段是如何分布?有什么样的知识脉络?
以“图形与几何”领域内容为例,它有如下知识点及年级分布:

一年级 二年级 三年级长方体,正方体,圆柱和球的直观认识。长方形,正方形,三角形和圆的直观认识。长方形和正方形的认识和周长。平行四边形的直观认识。面积的含义,长方形、正方形的面积。四年级 五年级 六年级直线和线段的初步认识。角的初步认识,直角。

直线的测定,测量距离,(工具测,步测,目测)。射线、直角、锐角、钝角、平角和周角。垂线,平行线及其画法。三角形的特征,分类与内角和。平行四边形和梯形的特征。平行四边形三角形和梯形的面积,组合图形。长方体和正方体的特征、表面积。体积的含义、长方体和正方体的体积。圆的认识,圆周率,画圆。圆的周长和面积。扇形的认识。轴对称图形的初步认识。圆柱的认识,表面积和体积。圆锥的认识和体积。球和球的半径、直径的初步认识。
从上表中不难看出图形几何领域包括了图形的认识、测量、运动及图形与位置。它从六个维度进行建构。第一,从立体→平面→立体,即:从直观的立体模型(长方体、正方体、圆柱体、球体)到抽象的平面图形(长方形、正方形、三角形、圆形)再到抽象立体图形(长方体、正方体、圆柱体、圆锥体、球体)。第二,从整体→局部→整体,即:整体直观感知(辨别、认识)→探究图形特征(构成要素的特征)→理解整体属性(图形与图形的从属关系)。第三,从定性感知→定量刻画,即:定性感受(摸、看)到简单定量描述(构成要素的特征描述)再到精确定量研究(周长、面积)。第五,从静止→运动,即:静态图形到平移、对称、旋转。 第六:从直线→曲线,即:直线型(长、正方形,长正、方体)→曲线型(圆、球)。有了如上的整体分析教师可以体会到数学知识间的联系,理解到数学知识的作用,做到前有铺垫,后有照应。读懂数学教材知识点的编排体系,教学时才能做到重点得以突出,难点得以突破,教学设计详略得当。
二、读懂教材知识点的内在联系
读懂知识点的编排体系、具体内容和各册、各单元知识点的分布,这只是了解到知识点的外在内容,我们还要对知识的内涵进行深入的剖析,思考这些知识点内在的联系是什么?
以“图形与几何”领域内容为例:直线、射线、线段属于一维空间,长方形、正方形、圆形、三角形属于二维空间,长方体、正方体、圆柱体、球等属于三维空间。线段的长短、长方形、正方形、三角形等平面图形的周长属于一维空间的计量,长方形、正方形、平行四边形、三角形、梯形、圆形平面图形的面积属于二维空间的计量,其中平行四边形、三角形、梯形、圆形面积是转化后的计量单位的计量,长方体、正方体、圆锥的体积是三维空间的计量。由此“图形与几何”领域的知识可作如下重构:

计量单位的认识 计量单位的计数一维(线)线与长度单位的认识 长度单位的度量二维(面) 面与面积单位的认识 面积单位的度量三维(体) 体与体积单位的认识 体积单位的度量
根据这一脉络,“图形与几何”领域知识其实就是解决:计量单位的认识、计量单位的计数。计量单位是一种标准比较物,计量单位的计数通常为工具度量,以及在度量基础上总结出形式化的计算公式,最典型的就是长方形面积公式的推导。其实长方形面积公式的推导原理就是数面积数。这个过程其本质就是操作计数到观察简约到思考发现再到一般规律的过程。同理,平行四边形面积公式的推导原理也是数面积数,只是它比长方形面积的推导多了一步,即:把平行四边形面积转化为长方形面积,其本质是相同的。
通过以上分析,不难看出“图形与几何”的内核及联系便是计量单位。这些领域知识通过计量单位来体现数学知识间的内在联系,以及联系中所蕴含的数学思考价值,才能达到数学教育的目的。有了这样的认识,老师们再去设计每一课时的学案就与“点对点”的设计有了本质的区别。
三、读懂各知识点地位及作用
各知识点分布在各册、各单元、各课时,各领域的知识点为什么要这样分布?处在整个单元的哪个位置?它有什么作用?与前后知识有什么联系?这些知识点是怎样一个一个串联起来,最终达成学习目标的呢?这就要求教师要深入地分析各知识点的地位及作用。
以“几何与图形”板块的“长度单位”这一单元为例作如下分析:“长度单位”这一单元教材通常会安排四个课时:即厘米的认识,分米的认识,米和毫米的认识,千米的认识。现将四个课时的知识点分析做如下分析:

课题厘米的认识分米的认识米和毫米的认识千米的认识知识点1、知道厘米这个长度单位,用cm表示2、建立厘米的表象3、用厘米作判断4、用厘米作度量1、知道分米这个长度单位,用dm表示2、建立分米的表象3、用分米作判断4、用分米作度量5、知道1分米=10厘米1、知道米和毫米这两个长度单位,分别用m和mm表示2、建立米和毫米的表象3、用米和毫米作判断4、用米毫米作度量5、 知 道1米=10分米=100厘米1、知道千米这个长度单位,用km表示2、建立千米的表象3、用千米作判断4、用千米作度量5、知道1千米=1000米
从四个课时的知识点来看,基本知识和基本技能大致雷同,前一课时有利于后一课的掌握,因为知识间可以迁移。但如果仅仅凭这个来做学案设计,一课时一课时的落实知识,学生越学越没有兴趣,教师越教越无味。因为基本知识与基本技能雷同,教学方法及策略就会雷同,即:让学生比一比、量一量、数一数、想一想等。究其根本原因是我们只从知识点在做简单分析,并没有剖析出这几个知识点的地位和作用。虽然它们双基雷同,但其地位和作用不同。现将四个课时的知识点的地位和作用做如下分析:

课题厘米的认识分米的认识米和毫米的认识千米的认识地位及作用计量单位是标准比较物问题:为什么要有单位?标准比较物具有适宜性。问题:既然有了厘米,为什么要学分米?标准比较物具有多样性。问题:往更大思考或往更小思考,分别有什么单位?标准比较物具有多样性。问题:往更大思考当用米作单位也不方便时还有什么单位?
像这样有了知识点的分析又有了其地位和作用的分析,教师设定每一课时学习目标,侧重点把握就更聚焦,然后根据每一个侧重点的不同,把侧重点做足,教师的教学中目标就会更清晰,重点得以突出,难点得以突破,知识的作用得以发挥,学生学起来才会更有趣。
四、读懂知识点的本质
对教材的解读,不能只关注显性的内容,不能被新奇的呈现方式所蒙蔽。优秀的教师要有一双透过现象看本质的慧眼,要有透过知识表象分析知识本质的能力。例如:“烙饼问题”,“烙饼问题”是人教版四年级上册第七单元数学广角第二个课时,题干为“一口锅每次最多能烙两张饼,两面都要烙,每面烙3分钟,烙熟5张饼一共要烙多少分钟?”。教材呈现的方法是让学生动手实验:烙一张饼的方法、所用时间是多少?烙两张饼的方法、所用时间是多少?以此类推,然后通过观察分类得出烙奇数张的方法及所用时间时多少,烙偶数张的方法及所用时间是多少。但“烙饼问题”的本质不是怎样烙,而是烙熟几张饼共需要烙几次?近而思考烙几次跟什么有关?通过推理得出:烙熟几张饼的时间=烙的次数×烙熟一面所需时间=(饼的张数×烙熟每张饼的次数÷一口锅一次最多能烙的次数)×烙熟一面所需时间(烙一个饼除外)。再如:“植树问题”的本质是包含除;“数学编码”的本质是编码的唯一性,简洁性;“角的度量”的本质是所量角中包含了多少个计量单位(1度)。在教学中如果教师不了解知识的本质,学生学习只会是机械的模仿,未能真正学会知识。教师只有抓住数学知识的本质去设计和实施教学,数学教育才能找到教学支点,才有利于知识的落实,重点的突出,难点的突破,从而实现教学目标。
五、读懂知识点背后蕴含的数学思想
数学教材的编排其实包含了两条线:明线和暗线。明线即显性知识,也就是我们平常说的“双基”(基本知识、基本技能)。隐性知识即隐藏在显性知识背后的数学思想。显性知识因为有具体的知识点,学生可以通过阅读来获得,但隐性知识没有明确的知识点,学生无法通过阅读获得。这就要求教师要充分挖掘隐藏在显性知识背后的数学思想,并在教学显性知识点时渗透、明确数学思想。
在小学数学知识中蕴含了许多数学思想,主要有这些思想:转化思想、分类思想、符号思想、集合思想、统计思想等等。例如:平面图形面积公式的推导过程(如图一)就蕴含了“转化思想”。先将平行四边形的面积等积转化为长方形的面积,转化后长方形的长就是原平行四边行的底,转化后长方形的宽就是原平行四边行的高。因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
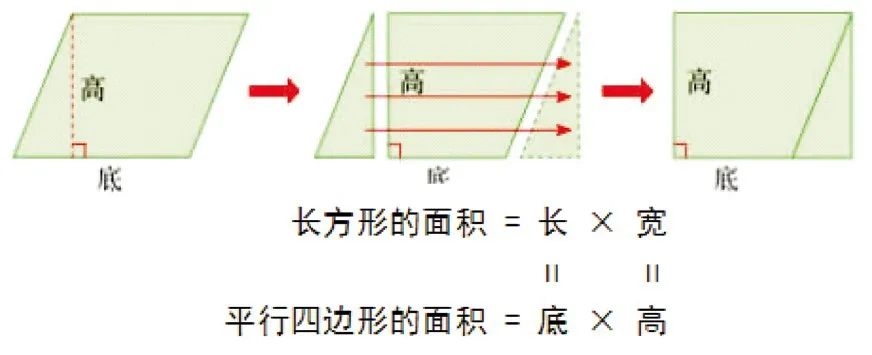
(图一)
当教师在推导平行四边形面积的教学过程中渗透、提炼了“转化思想”,在推导三角形面积、梯形面积公式的教学过程中学生就会运用类推的方法将三角形面积、梯形面积转化为平行四边形的面积,再观察、对比转化后的平行四边形面积与转化前的三角形面积、梯形面积有什么关系?从而推导出各自的面积公式。
再如:搭配(二)的知识点中蕴含了“符号思想”(如图二)。图二清晰的展示了从具体实物搭配到抽象符号搭配的过程,通过对比直观清晰的体现出符号思想解决问题的方便与便捷,表现出“符号思想”的价值。

(图二)
总之,作为教师,读懂教材是一项必备能力,是进行有效教学的基础。教师只有在读懂教材知识点的编排体系,知识点的内在联系,知识点的地位和作用,知识点的本质以及知识点背后的数学思想后,才能大胆地对教材内容进行选择、补充、改造等;才能灵活地运用教材,设计有意义、有价值的活动;才能进行有效教学,让学生在学会知识的同时,掌握方法,体会思想,提高学生的数学素养,从而促使学生的持续发展。◇

