协变量数据缺失情形下的参数估计方法
于力超
(中央民族大学 理学院,北京 100081)
0 引言
调查过程中常出现数据缺失,在这种情形下不能直接将含缺失值的个体信息全部删除而只利用数据完全的样本数据,因为数据缺失与否往往与该数据的具体值系统地相关,比如关心的因变量是受访者的年收入,高收入群体可能不愿意将自己的收入告知他人,这种情况造成的数据缺失就不能采用直接删除法,否则会造成估计结果偏低。为此收集尽量多的协变量数据就很有意义。可以采用插补法(包括回归插补法、近邻插补法)或似然法(通过建立因变量、协变量和缺失指示变量的分布模型)[1]。在这些方法中,以往研究都假设协变量数据没有缺失,回归插补法通过有回答的样本数据建立模型,代入因变量数据缺失样本的协变量数据以估计因变量值。近邻插补法通过定义距离函数,考虑用与因变量缺失个体的协变量最相似有数据的个体因变量值插补。似然法则引入数据缺失机制,通过建模得到因变量与缺失指示变量的联合分布,进而得到参数的极大似然估计。
实际调查中,协变量缺失的情况也是非常常见的,例如出于隐私考虑不愿公布年龄或婚姻状况,由于知识水平所限无法回答某些超出其知识范围的问题,也可能某些协变量收集难度大成本高,调查人员选择只收集一部分受访者的信息。协变量缺失时因变量可能没有缺失,也可能协变量和因变量同时缺失,这就大大增加了协变量关于因变量回归系数估计的难度。但目前国内外关于协变量缺失情形下尤其是缺失机制是非随机缺失时参数的估计方法研究还不多,Little(1992)[2]研究了回归分析中缺失协变量的处理方法,但其研究局限于因变量与协变量之间满足线性回归关系,且假设因变量Y与协变量向量X的联合分布为多元正态分布,Horton和Laird(1999)[3]研究了缺失机制为MAR的属性协变量缺失问题,通过建立广义线性模型,用极大似然法进行参数估计,Michiels等(1999)[4]用选择模型和模式混合模型建立似然函数,用极大似然法估计属性协变量数据缺失时的总体参数。在软件功能日益强大的今天,数据扩充算法、EM算法、Gibbs抽样法等迭代算法应用日益广泛。SAS Proc MI可以采用多重插补法进行协变量数据缺失情形下的参数估计。R有多个软件包可以进行缺失数据统计分析,ACD包可以在因变量数据缺失时进行属性数据分析,mvnmle包在因变量和协变量联合分布为多元正态分布时,进行协变量数据缺失情形下的参数极大似然估计,MICE包是R中目前最常用的用于缺失数据分析的软件包,可以进行多变量缺失数据的多重插补,在多个协变量都可能存在缺失值时,使用MICE包中的mice函数,通过变量之间的关系预测缺失数据,利用蒙特卡洛方法生成多个完整数据集存在imp中,再对imp进行线性回归,最后用pool函数对回归结果进行汇总。
本文尝试引入以上统计计算方法,采用多重插补法、Bayes法和极大似然法,在缺失机制为MAR或NMAR情形下,估计调查数据中协变量数据缺失情形下,协变量关于因变量影响大小的回归系数。
1 符号、概念及协变量缺失处理方法
1.1 符号表示
设共有N个受访者,因变量为Y,得到观测值yi,i=1,...,N,其中可能有缺失值也可能没有,同时对第i个受访者,调查与yi相关的p维协变量Xi,Xi=(xi1,...,xip),Nxp 维协变量矩阵X=(X1,...,XN)',假设 (Xi,yi),i=1,…,N独立同分布。协变量含有缺失值的情形下,记第i个受访者协变量的所有观测值为Xobs,i,缺失值为Xmis,i,Xi=(Xobs,i,Xmis,i), ,记 Nxp 维协变量缺失指示变量矩阵r=(r1,...,rN)',若第i个受访者的第k个协变量数据未缺失rik=1,否则rik=0。
1.2 数据缺失机制的概念
本文考虑协变量数据缺失的情形,为表述简便,假设收集到的样本数据中,因变量Y无缺失,协变量X有缺失(若Y也有缺失,则只需在迭代过程中增加一步:从Ymis,i关于(yobs,i,Xi)后验分布中抽取下一轮迭代的初值。除此没有本质上的差异)。此时定义的缺失机制与描述数据缺失与否与因变量数据之间的关系的常规定义不同,对于纵向缺失数据,缺失数据机制可分为完全随机缺失(MCAR)、随机缺失(MAR)和非随机缺失(NMAR),MCAR指变量数据缺失与否与变量的值无关,这时候缺失数据集是总体数据集的一个简单随机样本,仅用观测数据就可得总体参数的无偏估计,协变量缺失时MAR指协变量是否缺失仅与已经观测到的协变量值有关,即L,可见在给定Xobs,i时,Xmis,i与ri独立,即,可以忽略缺失值,仅用完全观测数据对总体参数进行估计,这就是MAR被称为可忽略缺失机制的原因。
2 插补法处理缺失协变量
2.1 完全数据法
该方法将所有含缺失值的受访者删除,仅保留完全数据样本进行统计分析,这种方法仅当缺失机制为MCAR时可以得到参数无偏估计,缺失机制为MAR或NMAR时得到的估计量有偏,若协变量数目较多,即使某受访者只有一个协变量数据缺失,仍需要将其所有数据删去,这样可能导致可用的数据量不足,造成大量的信息浪费。虽然这种方法经常采用,但并不值得推荐。
2.2 可用信息法
该方法利用所有可利用的信息进行参数估计,若N个受访者中,第k个协变量有观测值的受访者个数为Nk,则第k个协变量的期望μk就用这Nk个数据的均值估计;若N个受访者中,第j个和第k个协变量都有观测值的受访者个数为Njk,则第j个协变量和第k个协变量之间的协方差σjk用这Njk个受访者的相应观测数据计算。但此时关于第


由上可见,如何获得协变量缺失值的插补值是关键,这就要求获得后验分布:

具体地,若协变量X均为离散型,则:
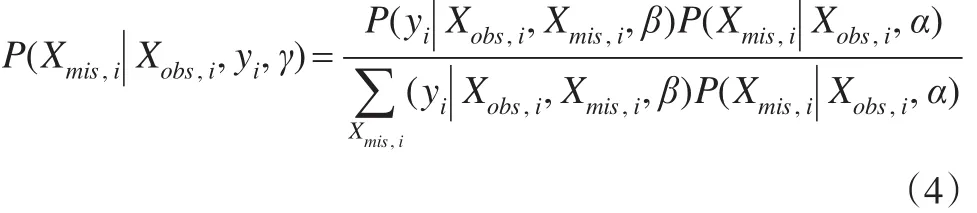
分母中是对第i个受访者所有缺失协变量的所有可能取值求和。若协变量均为连续型,则分母中求和号改为积分号。一般情况下,协变量既有离散型又有连续型,记第i个受访者离散型协变量缺失值的所有可能取值集合为,连续型含缺失值协变量集合记为,缺失值的可能取值集合为Ω,则:

由式(3)可见,为获得插补值Xmis,i,需要获得Xmis后验分布P(Xmis,i|Xobs,i,yi,γ)的参数γ,然后从该后验分布中抽取Xmis,i,获得参数γ的方法有两种:在软件SAS Proc MI中,假设(Yi,Xobs,i,Xmis,i)服从多元正态分布,并假设协变量的缺失机制为MAR,由于MAR为可忽略缺失机制,可以仅通过观测的数据对总体参数进行估计,通过软件可以得到P(Xmis,i|Xobs,i,yi,γ)中参数γ的极大似然估计̂,代入Xmis,i的后验分布,然后从P(Xmis,i|Xobs,i,yi,̂)中多次抽取Xmis,i,从而得到多个插补数据集进行参数估计。但这种方法需要做总体服从多元正态分布的假定。i个受访者第j个协变量和第k个协变量之间的p阶相关矩阵不一定正定,若非正定,协变量X与因变量Y之间的回归系数β将无法确定。
2.3 多重插补法
采用多重插补法进行参数估计的基本步骤如下[5]:第一步:抽取符合缺失变量后验分布的插补值,重复进行M次得到M个“完整”数据集;
第二步:对第m个插补后的“完整”数据集进行参数估计,记待估参数为γ,得到估计值γ̂(m),其中m=1,…,M。第三步:参数估计为:
下面采用Gibbs抽样获得插补值的方法更加合理。
根据式(3),后验分布P(Xmis,i|Xobs,i,yi,γ)中的参数γ包括P(yi|Xi,β)中的参数β和Xi边缘分布中的参数α,Gibbs抽样分两步进行:
第一步:从观测值(Yi,Xobs,i)已知时(β,α)的后验分布中抽取(β,α)参数值,由于已知观测值时(β,α)的后验分布形式未知,实际操作中简便起见常取无信息分布(例如定义域上的均匀分布)作为(β,α)的后验分布。为了充分利用观测值信息,建议通过数据扩充算法(Data augmentation)[6]来实现对 (β,α)的 Gibbs抽样。数据扩充算法基本思想体现在下面两个式子中:
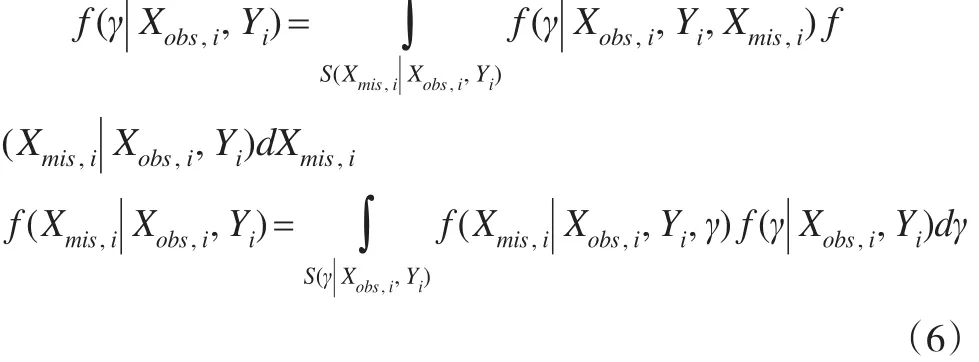
其中S(Xmis,i|Xobs,i,Yi)和S(γ|Xobs,i,Yi)分别为在给定观测值条件下,协变量缺失值和参数分布的支撑集。综合以上两式,可以得到参数后验分布的迭代算法,设第k步迭代得到参数γ的后验分布为fk(γk|Xobs,i,Yi),则第 k+1步参数γ的后验分布为:

Tanner和Wong(1987)证明了在一定正则条件下,fk+1依分布收敛于参数的后验分布
根据以上两式,本文建立了迭代算法:
首先,设定参数的初始值γ0开始迭代,在第k步参数后验分布中抽取 m个参数值,对每
其次,将第k步的m个插补值代入数据集得到m个完整数据集(当缺失机制为不可忽略时,无法仅通过观测值(Yi,Xobs,i)得到总体参数的后验分布,插补后通过完整数据集则可以得到参数的后验分布,这是数据扩充算法的意义所在),通过这m个完整数据集下参数的后验分布可以得到第k+1步参数的后验分布:
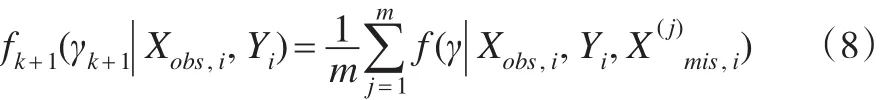
如此迭代进行,可以得到参数γ的后验分布中 取γ(r)代 入中 抽 取,如此重复进行m次,得到m个完整数据集,进而用对完整数据集用式(1)和式(2)进行参数估计。
3 似然法处理缺失协变量
3.1 Bayes估计法
用Bayes法进行缺失协变量情形下的参数估计,基于观测值(Yi,Xobs,i)估计P(yi|Xi,β) 中的回归参数β和P(Xi|α)中的协变量分布参数α,设(α,β)的先验分布为p(α,β),损失函数为平方损失,则参数的Bayes估计为给定观测值条件下参数的后验期望。参数的后验分布函数:
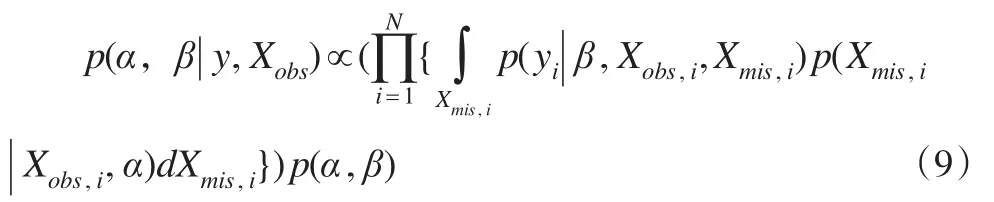
其 中y=(y1,...,yN) ,Xobs=(Xobs,1,...,Xobs,N) ,Xmis=(Xmis,1,...,Xmis,N)。该后验分布函数不容易有显示表达式,采用如下步骤获得参数的Bayes估计。
第一步:确定参数 (α,β)的联合先验分布p(α,β),可以假设p(α,β)=p(α)p(β)即α,β的先验分布相互独立,这样可以对α和β分别假定先验分布(如定义域上的均匀分布或正态分布),在Gibbs抽样时分别从两个先验分布中抽取参数值,也可以假设p(α,β)≠p(α)p(β),这样需要对(α,β)假设联合先验分布,如二元正态分布或二维均匀分布,从中抽取参数值用于后续Gibbs抽样。
第三步:Gibbs抽样以获取满足后验分布p(α,β|y,Xobs)的样本。抽样方法如下:
①通过第一步抽取 (α0,β0);
② 根 据 式(4)从p(Xmis,i|yi,Xobs,i,α0,β0) 中 抽 取,从而获得第i个受访者的完整数据集Xmis,i);
③进行第一次迭代,得到参数β后验分布p(β|yi,,从中抽取β1;
④获得参数α的后验分布从中抽取α1,这样就得到第一次迭代后的参数值(α1,β);
……
重复上面的迭代过程,直到(α,β)收敛,这样就得到一组满足后验分布为p(α,β|y,Xobs)的参数值,记为(α1,β1),重复m次这一迭代过程,得到m组参数值(αi,βi),i=1,...,m,参 数 的 Bayes估 计 量 可 以 用
以上方法假设协变量缺失机制为MAR,若缺失机制为NMAR,后验分布函数为:

可以容易地将上面的方法推广到协变量缺失机制为NMAR的情形。
3.2 EM极大似然估计法
在协变量含缺失值的情形下,常采用EM算法[5]求参数的极大似然估计,EM算法是一种迭代算法,每次迭代分两步进行。假设协变量的缺失机制为NMAR,首先设定参数的迭代初值γ(0)=(α(0),β(0),ϕ(0)),设第 t步迭代后得到的参数估计值为γ(t)=(α(t),β(t),ϕ(t)),第t+1步迭代(t≥0)如下:
E步:根据(yi,Xi,ri)的联合分布p(yi,Xi,ri|α,β,ϕ)=p(yi|Xi,β)p(Xi|α)p(ri|yi,Xi,ϕ),写出对数似然函数,其中我们最感兴趣的参数是协变量与因变量之间的回归系数β。
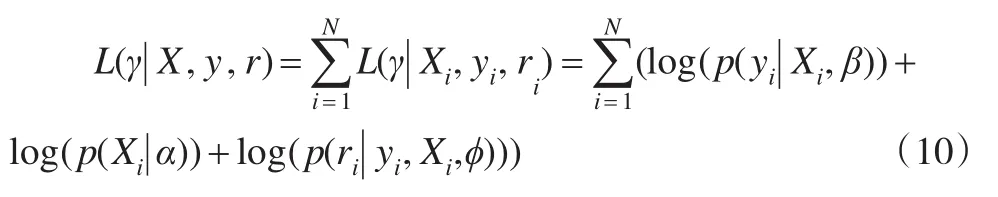
由于没有Xmis,i的信息,需要将其通过积分或求和去除,写出给定观测值条件下Xmis,i的密度函数,求对数似然 函 数 关 于 该 条 件 密 度 的 期 望 ,即|Xobs,i,Yi,ri],当缺失协变量为连续型变量时:
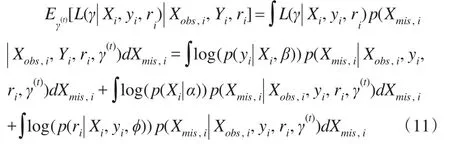
若缺失协变量为离散型,积分换为对缺失协变量的所有可能值求和,条件分布p(Xmis,i|Xobs,i,yi,ri,γ(t))可以在式(4)基础上将观测值ri合并入无缺失观测值yi,但这时显式表达式不容易获得,尝试采用Gibbs抽样的方法获得缺失 协 变 量 数 据 集 ,具 体 地 ,,采用 Gibbs抽样的迭代思想,在第 t步参数γ(t)=(α(t),β(t),ϕ(t))已知的条件下,设Xmis,i为 p1维 向 量,Xobs,i为 p2维 向量,p1+p2=p,从中Gibbs抽样,其中Xmis,ik为p1维向量Xmis,i的第k个分量。具体步骤如下:

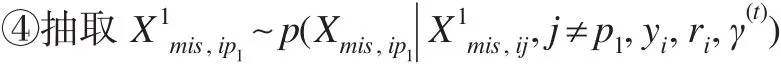

对所有受访者E得到的结果为:

一般情况下,我们主要关心的参数是反映协变量与因变量之间的关系的β,所以α和ϕ为冗余参数,只需对求最大值得到β(t+1),它是第t次迭代M步的解,也是第t+1次迭代E步的参数值。
4 模拟案例
本文通过一个模拟案例比较本文的三种方法(多重插补法、Bayes法、EM极大似然法)与只采用完整数据集(删去含缺失数据的受访者)进行回归分析的完全数据法之间的优劣。设样本量N=250,第i个个体因变量yi为0-1变量,协变量Xi=(Xi1,Xi2,Xi3),yi通过如下logistic模型独立生成:
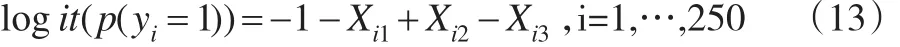
采用如下方式生成协变量值:
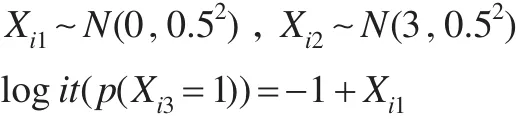
假设Xi1和Xi2无缺失值,Xi3的缺失机制如下:

可见协变量的缺失机制为MAR而非MCAR,使用完全数据法得到的参数估计有偏。采用上面的数据生成方法,得到1000组样本量为250的模拟数据。在采用上述协变量数据缺失机制,得到1000组含缺失的模拟数据。用模拟生成的数据对模型(14)进行参数估计,看估计结果与本文设定的模型(13)之间的符合程度。

在用Bayes法时,设先验分布为无信息先验π(β)∝1,在多重插补法中,设插补后得到M=5个完整数据集。为获得基于模拟数据参数估计的标准差(SE)和均方误差(MSE),对于多重插补法,采用式(2),对于EM极大似然法,采用Ibrahim等(1999)[7]的方法,对于Bayes法,根据上文所述,通过Gibbs抽样,在Markov链 (αi,βi)收敛后得到m组 (αj,βj),j=1,...,m,取 m=20,可求的标准差和均方误差。所得结果如表1所示。
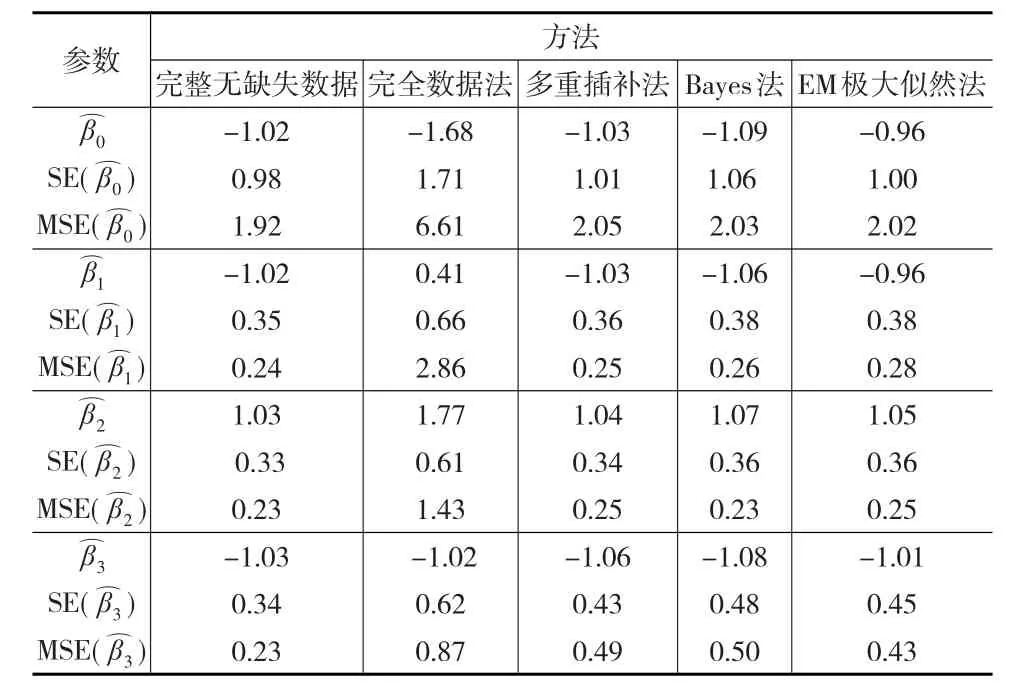
表1 本文三种方法与完全数据法参数估计模拟结果比较
由以上模拟结果可见,用完全数据法直接删去协变量含缺失数据受访者的所有数据,仅用完全数据样本得到的结果与初始模型(13)相比偏差较大,参数估计的标准差和均方误差也明显大于本文其他三种方法所得结果。所以不推荐使用完全数据法进行参数估计。
采用多重插补法、Bayes法和EM极大似然法在协变量含缺失数据情形下进行总体参数估计所得结果并无明显优劣之分,从无偏性和有效性的两方面看都可以较好地估计总体参数,可以根据实际情况选择合适的方法进行协变量数据缺失情形下的参数估计。
5 总结
本文尝试采用EM算法、Gibbs抽样法和数据扩充算法等统计计算方法,采用多重插补法、Bayes法和极大似然法,在缺失机制为MAR或NMAR情形下,估计调查数据中协变量数据缺失情形下,反映协变量X对因变量y影响大小的回归系数。
研究可以进一步推广到协变量和因变量同时缺失的情形下定义缺失机制、建立似然模型并采用统计算法进行回归系数估计。还可以推广到对多个体多时点纵向调查,在协变量缺失的情形下,引入统计算法,进行回归系数估计。

