基于推断模型的Behrens-Fisher问题的精确检验
梁成扬,金 华,何美仪,谭银冰
(华南师范大学 数学科学学院,广州 510631)
0 引言
非劣检验指主要研究目的是显示对试验药的反应,在临床意义上不差于(非劣于)对照药的试验。设A药为待确证疗效的试验药,B药为对照药,下同。非劣检验的假设检验如下:
原假设H0:A药疗效-B药疗效≤-δ
备择假设H1:A药疗效-B药疗效>-δ
如果p>0.05,按单侧α=0.05的检验水准不能拒绝H0假设,即无法判断A药不差于B药;如p≤0.05,则接受H1假设,可认为A药不差于B药。假设服用A药的样本为,服用B药的样本为上述非劣检验问题等价于:

在统计学上,该问题也称为Behrens-Fisher问题。
针对上述问题,Welch[1,2]给出一种基于随机自由度的近似方法(常称为Welch近似t检验),他认为检验统计量在原假设H成立时近似服从自由度
0为l的t分布,其中自由度(非整数时四舍五入)。l=Scheffe[3](1970),Best 和Rayner(1987)[4],以及 Moserb和Stevensg(1989)[5]都认为:如果既要考虑检验的无偏性,又要兼顾实际应用的方便,Welch近似t检验或许是最好的方法,因为它只需t分布表,而Welch-Aspin检验的临界值计算相当麻烦。现在的大学教科书大都采用Welch近似t检验这种方法[6,7]。但是该方法下的检验结果不能很好地控制住第一类错误。
最近学术界提出了一种新的推断体系,称为推断模型(Inferential Model,简记为IM)体系,而IM体系来源于对置信及其拓展——信仰函数的Dempster-Shafer理论的探讨。IM的原创基本思想来自Martin等[8]、Zhang和Liu[9]以及Zhang[10]文中提出的对Dempster-Shafer理论修正。推断模型方法发表在国际统计学最顶尖的杂志Journal of the American Statistical Association和Journal of the Royal Statistical Society上,所以基于IM模型,下面给出精确检验方法。而且通过模拟验证,基于IM模型的方法可以控制住第一类错误,比Welch近似t检验好。
1 基于推断模型的方法
对于此问题,可以转化为对断言A={μ1-μ2:μ1-μ2≤-δ}={μ:μ≤-δ}的推断,其中μ1-μ2=μ
根据文献[11,12],得到条件联结模型:
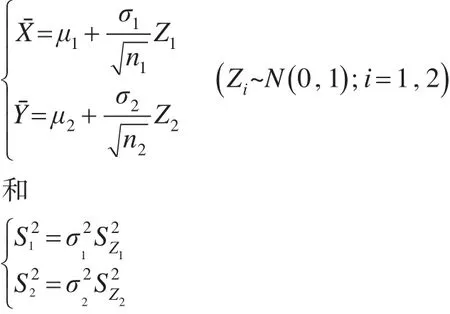
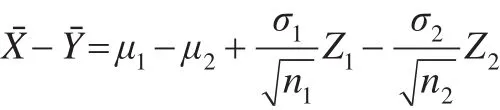
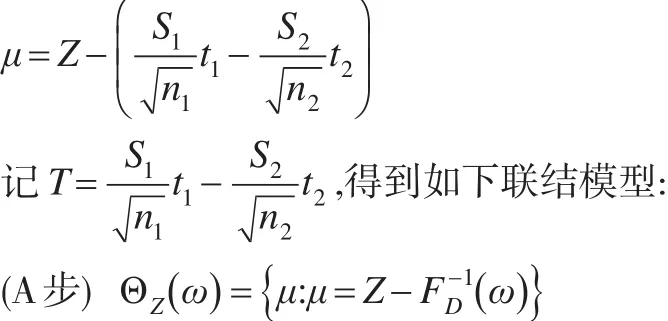
其中辅助变量为ω=FD(T)且ω~U(0 ,1),FD(·)为给定样本X1,X2,...,Xn1,Y1,Y2,...,Yn2后T的条件分布函数。
(P步) 对断言A来说,辅助变量ω的随机预测集是:

(C步) 组合ΘZ(ω)和S得到μ的随机预测集:

于是断言A的可能性函数为:
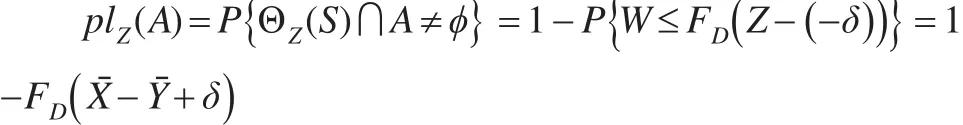
此方法是有效的(证明略),但由于FD(·)给定样本后的条件分布函数,此分布的概率密度函数是未知的,从而无法直接计算plZ(A)的值,故需要利用计算机模拟计算其估计值:
给定X1,X2,...,Xn1,Y1,Y2,...,Yn2后,分别产生n个t1与t2随机数,其中t1~t(n1-1),t2~t(n2-1),记m为T≤-+δ的个数,利用频率估计概率的方法,得:

则plZ(A)的估计值为:

但是,为了确保估计的精度,即:
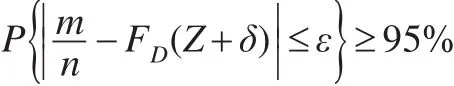
对于给定的最大允许误差,需要重复的次数大约为:
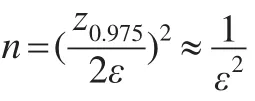
然而此估计值并不是plZ(A)的真实值,当p̂≤α时,并不意味着有plZ(A)≤α。plZ(A)有95%的概率落在的置信区间上。为保证精度与可信性,考虑到本文的非劣检验为右侧检验,故使用做统计推断。这里,本文选择n=10000。
2 模拟实验及结果
2.1 实验结果
为比较小样本情形下Welch近似t检验和基于推断模型的新方法的第一类错误,本文利用R语言编程进行随机模拟。
为考察两种方法的第一类错误,取显著性水平α=0.05,重复试验200000次,则其置信水平为95%的置信区间为(4 .904%,5.096% )。
2.2 结果分析
根据模拟结果来看,在样本量不等的小样本情况下,Welch近似t检验的第一类错误率大部分(58.3%)都超过了预先指定的显著性水平α=0.05的置信上限;只有在样本量相同的情况下,频率方法才可以控制第一类错误。而在本文模拟的所有情况下,推断模型的第一类错误率都较为接近5%,表明推断模型方法能保证控制第一类错误。对于功效,推断模型方法与Welch近似t检验相差不大,比较接近。
综上,在样本量不等的情况下,推断模型方法要比Welch近似t检验优,而在样本量相等的情况下,两种方法相差不大。
3 总结
本文提出了基于推断模型的非劣检验的新方法,通过比较频率方法的Welch’s近似t检验,发现推断模型有重要的应用价值,它可以完全控制第一类错误,不需要大量重复试验就可以得到理想的结果,这对医学药效检验具有重大意义。然而,推断模型的结果较为保守,难以作出精确的判断,还是需要对具体问题进行具体分析。本文总结的这个推断模型方法可以为实证研究人员提供一些参考,可以尝试应用在医学药效检验的领域中。

表1 Welch近似t检验(T)和推断模型(IM)的第一类错误模拟比较

