基于图像融合技术的Retinex图像增强算法*
常 戬,刘 旺,白佳弘
(辽宁工程技术大学软件学院,辽宁 葫芦岛 125105)
1 引言
作为人类获取信息的主要途径之一,数字图像被广泛地应用在航空航天技术、生物医学、军事公安、视频和多媒体技术以及电子商务等众多领域[1]。然而,受光照、天气、采集设备等因素的制约,实际获得的图像往往存在光照不均、细节丢失等问题,严重影响图像信息的传达。因此,采用图像增强技术来提升图像的质量和视觉效果具有重要的应用价值。
当前,图像增强算法可分为空间域算法和频率域算法两大类。其中,空间域算法通过直接处理图像的像素值来达到图像增强的目的,而频率域算法则是通过修改图像的傅里叶变换来达到图像增强的目的。目前国内外的图像增强算法主要包括线性变换、伽马校正、直方图均衡、反锐化掩膜、同态滤波、色调映射、暗通道算法、基于形态学的图像增强算法、基于人类视觉系统的图像增强算法、基于偏微分方程的图像增强算法等。其中,直方图均衡算法通过在整个灰度级上均匀地扩展图像的直方图来达到增强图像对比度、丰富图像细节的目的。但是,在均衡直方图的过程中,原始图像中像素个数较少的灰度级被归并到了新的灰度级上,这会导致图像局部过增强且丢失细节[2]。反锐化掩膜通过加强原始图像中的边缘轮廓等高频信息来达到图像增强的目的[3],但增强后的图像在边缘处存在光晕现象,且光照变化平缓的区域增强幅度较小[4]。偏微分方程具有图像统计建模的简单性和灵活性以及数值实现中数学易处理性和有效性等优点,在图像增强中引起了广泛的关注[5]。色调映射基于对比度增强技术,构建了基于概率的像素映射函数,然而,经常会为平滑区域分配一个较大的动态范围,从而阻止了对感兴趣的区域动态范围资源的分配[6]。
近年来,Retinex理论逐渐成为图像增强、图像去雾等领域中的研究热点。20世纪70年代,美国物理学家Edwin Land首次提出Retinex理论[7],该理论认为人们所观察到的图像是在入射光和反射光的共同作用下形成的[8]。随后,学者们基于该理论又提出了很多改进的Retinex算法,例如:随机路径选择法[9]、基于同态滤波的Retinex算法[10]、基于泊松方程的Retinex算法[11]等。20世纪90年代,Jobson等人[12]提出单尺度Retinex算法、多尺度Retinex算法等以中心环绕理论为核心的Retinex算法。2015年,Lee等人[13]提出基于Retinex的低光级图像的色彩保持对比度增强。2016年,Zhang等人[14]提出基于引导滤波和Retinex的彩色图像增强算法。2016年,Liu等人[15]提出基于自适应深度图的Retinex图像去雾算法。2016年,Song等人[16]提出基于遗传算法和人类视觉系统的自适应Retinex算法。2017年,Park等人[17]提出基于Retinex模型的变分优化的低光图像增强。Retinex算法凭借其实现简单、增强效果显著等优点得到了学者们的广泛研究。然而,Retinex理论遵循光照强度一致性假设,认为图像的光照强度的变化是均匀的,这导致增强后的结果图像在边缘等光照对比强烈的区域产生光晕现象。此外,传统单尺度Retinex算法仅对图像进行全局增强处理,没有考虑到图像的局部特征,导致增强后的图像对比度较低、图像泛灰[18]。针对单尺度Retinex算法存在“光晕”现象的不足,文献[19]提出采用双边滤波替换高斯核函数来估计光照图像,并将改进算法应用于人脸识别领域。基于双边滤波的Retinex算法能够较好地克服光晕现象,但仍然没有解决图像泛灰的问题。
为克服传统单尺度Retinex算法的光晕现象和图像泛灰的不足,本文提出一种基于图像融合技术的Retinex图像增强算法。针对光晕现象,参照文献[12],结合Jian等人[20]提出的加权滤波思想,即提炼出高斯加权双边滤波,并用其替换传统的单尺度Retinex算法中的高斯核函数,有效地去除了光晕现象。针对泛灰问题,本文将图像融合思想引入到传统算法中。首先,采用非线性变换拉伸反射图像并运用Otsu阈值分割算法获取图像的阈值,将像素值大于阈值的部分看作图像的亮区域,相反地将像素值小于阈值的部分看作图像的暗区域;然后,以信息熵为评价标准通过遍历非线性变换的参数的方式获得亮区域信息熵最大的图像(亮区域最优图像)和暗区域信息熵最大的图像(暗区域最优图像);最后,将亮区域最优图像、暗区域最优图像以及原始图像采用分块融合的方法进行融合,得到结果图像。加入原始图像是为了在充分增强图像细节的同时,避免过增强现象,从而获得清晰、自然的图像增强效果。
2 算法基础
2.1 Retinex理论
Retinex是由美国物理学家Edwin Land提出的一种自适应图像增强理论。该理论是模仿人类视网膜和大脑皮层在人眼视觉系统成像过程中的工作模式所提出的[21]。公式可表示为:
S(x,y)=R(x,y)×L(x,y)
(1)
其中,S(x,y)为原始图像,L(x,y)为光照图像,R(x,y)为反射图像。Retinex理论的思想是减少甚至消除光照图像对视觉效果的影响,保留反映图像本质属性的反射图像[22],从而达到图像增强的目的。
单尺度Retinex图像增强算法是Retinex理论相关算法中应用极为广泛的一种。该算法首先采用高斯核函数估计光照图像,然后从原始图像中消除光照图像的影响,达到图像增强的效果,其实现过程如式(2)所示。
R(x,y)=logS(x,y)-log[F(x,y)*S(x,y)]
(2)
其中,*表示卷积运算,F(x,y)为高斯核函数,即:
F(x,y)=ρ×e-(x2+y2)/σ2
(3)
其中,e为常量且e≈2.71828,σ为高斯环绕尺度,ρ为归一化系数,需要满足:

(4)
将像素值转换到对数域处理主要有两个方面的原因:一方面,对数域的运算将复杂的乘除法转换为简单的加减法;另一方面,对数域的数据更加接近人眼的感知能力[23]。
单尺度Retinex图像增强算法易于实现,且具有较好的图像增强效果。然而,该算法仍然存在以下的不足:
(1)由于Retinex理论假设图像的入射光是均匀变化的。而在实际的应用中,这一假设往往难以得到满足,特别是在图像的边缘等光照变化较为强烈的区域,容易产生“光晕”现象。
(2)传统的Retinex图像增强算法对图像整体进行全局增强,没有考虑到图像的局部特征,导致增强后的图像对比度较低、图像泛灰,视觉效果不自然。
2.2 图像融合算法
图像融合作为信息融合技术的一个重要分支,充分地利用图像的互补信息,将同一观察对象的多幅图像整合为一幅高质量的结果图像[24]。近年来,随着学者们对传感器领域的持续研究与拓展,图像融合技术也被越来越广泛地应用在各领域中。目前,图像融合技术的研究重点在于对两幅或多幅已有图像进行融合操作,在图像增强领域的应用还比较少,仍然存在很大的研究空间。
图像融合技术分为像素级图像融合、特征级图像融合以及决策级图像融合三个部分[25]。其中,像素级融合是后两个层次的图像融合的基础,也是图像融合领域近年来的研究热点,它通过直接处理图像的灰度值来达到图像融合的目的。像素级图像融合技术包括空间域融合和变换域融合。其中,空间域融合的常用方法有:加权平均法、对比度调制法、主成分分析法;变换域融合的常用方法有:金字塔法、小波变换法。
分块图像融合方法作为空间域图像融合的研究热点,首先将图像划分为特定尺寸的子块,然后针对每一子块,根据质量评价标准从两幅或多幅待融合图像中选择最优子块,并将筛选出的最优子块重新组合起来,构成高质量的结果图像[26]。
为了在最大程度上增强图像的细节,同时克服传统算法存在的图像泛灰问题,本文在图像的增强过程中引入图像分块融合算法,并选择信息熵作为最优子块的选取准则。
3 本文算法
3.1 光照图像估计
光照图像估计是Retinex图像增强理论的核心步骤,光照图像估计方法的选择会在一定程度上影响图像的增强效果。针对传统的单尺度Retinex算法容易产生光晕现象这一不足,本文采用高斯加权双边滤波来估计光照图像。
传统单尺度Retinex图像增强算法以光照一致性假设为基础,采用高斯模型估计光照图像。然而在实际应用中,图像的光照强度往往并不是一致的。因此,增强后的图像在光照变化强烈的边界区域容易产生光晕现象。双边滤波是在高斯滤波的基础上提出的一种改进算法,它在高斯滤波的基础上增加了与光照强度相关的参数。采用双边滤波进行光照图像估计的表达式如式(5)所示:
(5)
其中,p表示滤波窗口尺寸,S(i,j)为输入图像,L(i,j)为估计出的光照图像,α为与像素间空间距离相关的系数,β为与光照强度相关的系数。α和β的表达式如下所示:
α=e-σd×((i-m)2+(j-n)2)
(6)
β=e-σl×(d(i,j)-d(m,n))2
(7)
其中,(i,j)为邻域中心像素点的坐标,(m,n)为邻域内其他像素点的坐标,σd为距离差尺度参数,σl为亮度差尺度参数。双边滤波在高斯滤波的基础上增加了对像素点间亮度差异程度的考虑。将双边滤波引入到传统单尺度Retinex算法中,能够有效地改善由于光照强度不均匀所导致的光晕现象。
高斯加权双边滤波是在双边滤波的基础上提出的一种改进算法,它通过改进双边滤波中与光照强度相关的参数来达到调整像素点间亮度差异程度的目的。改进后的参数的表达式如下所示:
β=e-σl×(|d(i,j)-d(m,n)|-γ)2
(8)
其中,参数γ的取值会影响图像滤波的效果,当γ取值过小时,不能有效缩小像素点间的亮度差异,滤波效果等同于传统双边滤波;当γ取值较大时,会增加像素点间的亮度差异,导致光晕现象。大量实验表明,当γ=20时,采用高斯加权双边滤波估计光照图像能够有效消除光照强度不一致导致的光晕现象,从而获得清晰、无光晕的图像。
采用高斯加权双边滤波估计出光照图像后,依据Retinex理论去除光照图像对视觉效果的影响,就可以得到反映图像本质属性的反射图像。反射图像的计算公式如式(9)所示。
R′(i,j)=logS(i,j)-k×logL(i,j)
(9)
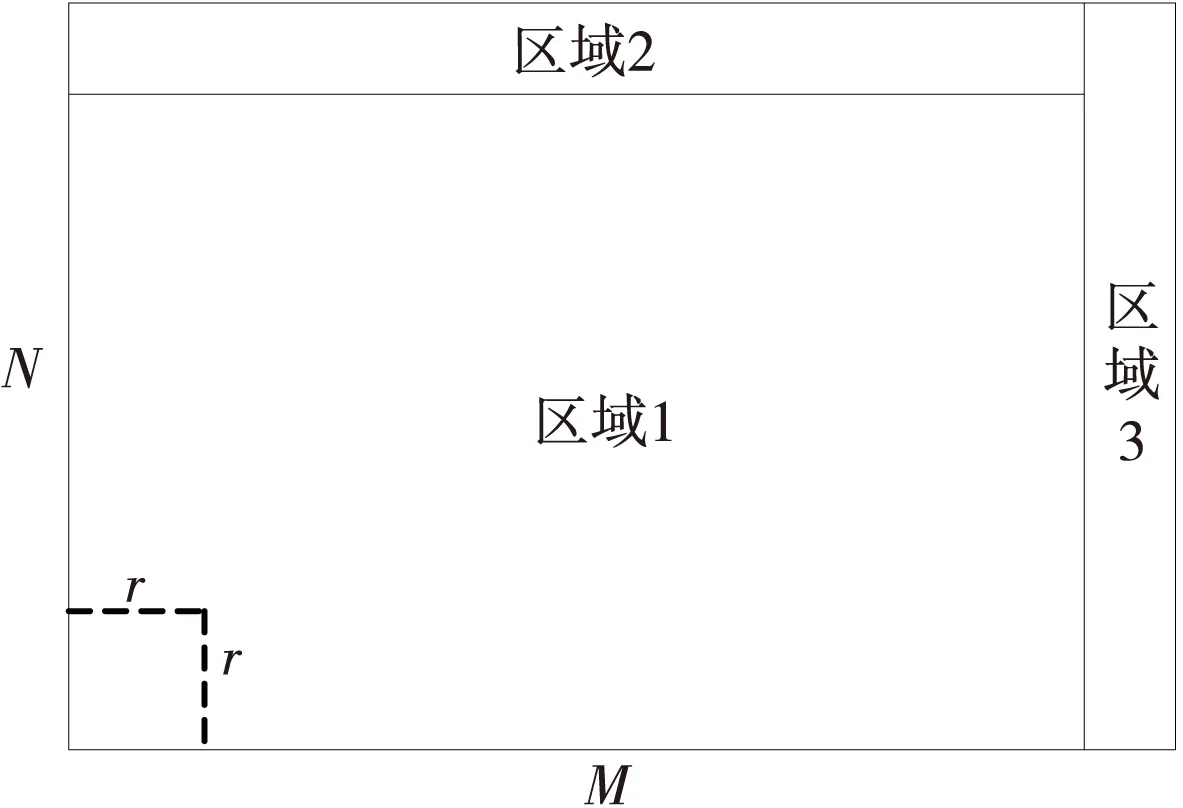
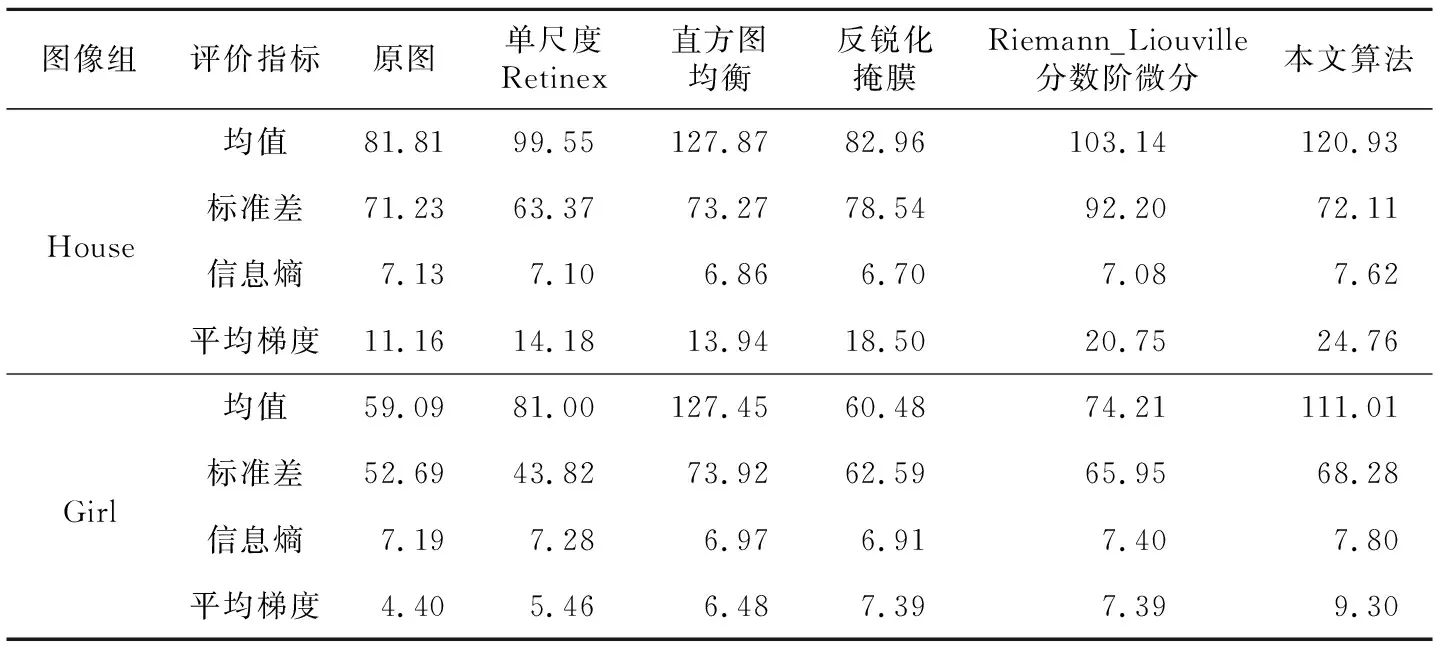
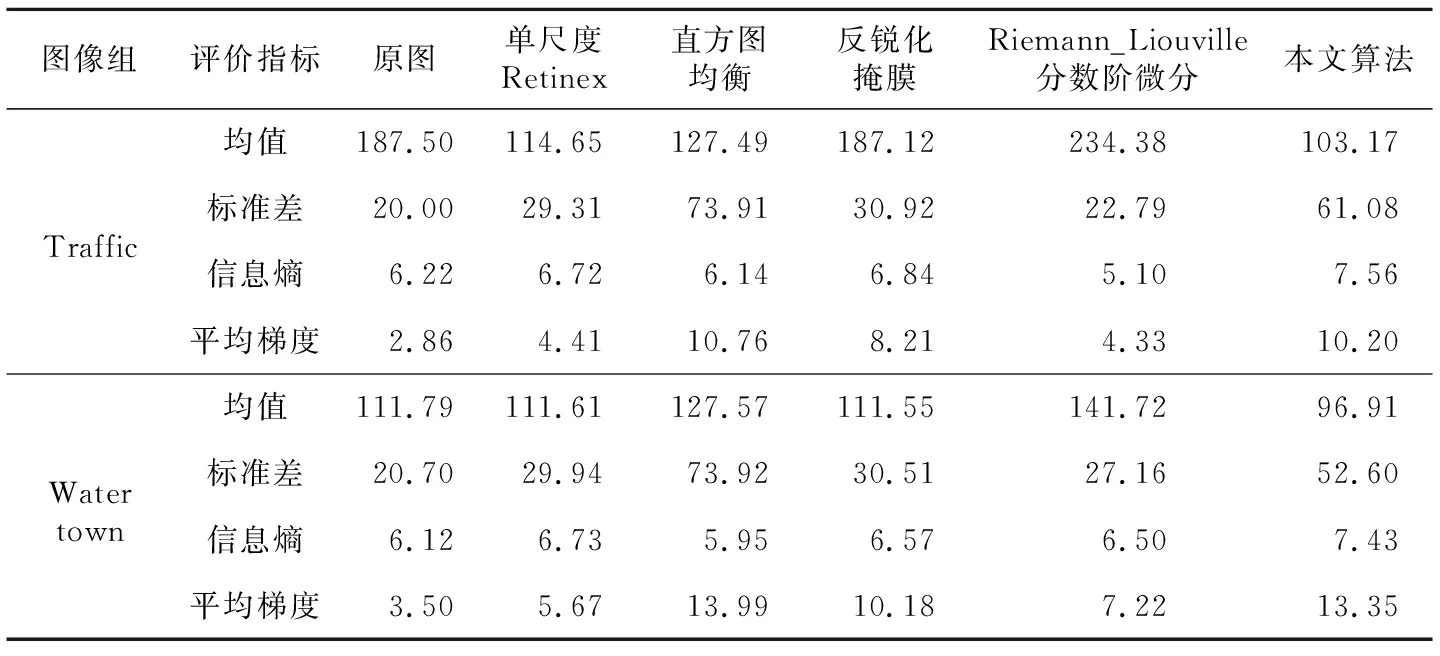
为使图像更加自然,引入增益参数k(0 采用高斯加权双边滤波来估计光照图像能够有效地克服光晕现象。然而,由于单尺度Retinex算法只在全局上对图像进行增强处理,忽略了图像不同区域的局部特征,在增强后的图像中,暗区域细节得到显著增强,而亮区域对比度下降,图像泛灰,如图1所示。为使图像的亮、暗区域都得到最大程度的增强,本文提出图像融合的思想,通过融合局部最优图像的方法来获得高质量的全局最优图像。如何获取原始图像的局部最优图像是此刻要解决的首要问题。 Figure 1 Grey phenomenon of Retinex theory图1 Retinex理论的图像泛灰现象 3.2.1 非线性变换 针对单尺度Retinex算法的图像泛灰的不足,本文采用灰度变换方法来量化反射图像,进而增强图像的对比度。灰度变换方法包括线性变换和非线性变换两种。其中,线性变换实现简单,但往往无法充分满足图像增强的要求。非线性变换通过灵活地调整变换曲线的斜率,能够对图像的不同区域实现不同程度的增强。常用的图像非线性变换方法包括对数变换、幂率变换等。本文所使用的非线性变换的公式如式(10)所示。 (10) Figure 2 Curves of the nonlinear transformation varied with different λ图2 参数λ取不同值时对应的非线性变换曲线 由图2可知,当λ取值较小时,曲线接近于线性变换,图像拉伸程度比较均匀,结合Retinex图像暗区域增强效果显著的特征,在拉伸后的结果图像中,原图像的暗区域的增强效果显著,而亮区域对比度不足、图像视觉效果偏灰。随着λ取值的增大,R′(x,y)值较小的区域拉伸后像素值接近于0,而R′(x,y)值较大的区域曲线斜率较大,结果图像中亮区域的增强效果显著,但暗区域的细节缺失较多。因此,当λ取不同值时,图像亮、暗区域分别取得不同程度的增强效果。本文通过调整非线性变换参数的方式来获得亮区域最优图像和暗区域最优图像,进而通过图像融合算法获得全局最优图像。 3.2.2 最优参数的选取 在局部最优图像获取的过程中,主要有两个影响参数,分别为式(9)中的增益参数k和式(10)中非线性变换的参数λ,合理选取这两个参数,对于图像增强的最终结果具有至关重要的作用。 本文采用梯度上升算法[28]来选取亮区域最优参数kmaxl、λmaxl和暗区域最优参数kmaxd、λmaxd。在求取最优参数的过程中,以信息熵最大化作为参数的选取依据。信息熵用来衡量图像中所包含的信息量的丰富程度,信息熵越大则表明图像所包含的信息越丰富,图像细节增强效果越好。图像信息熵的计算公式如式(11)所示。 (11) 其中,l表示[0,255]内的某一像素值,p(l)表示该像素值在图像中所占的比例。本文采用梯度上升算法获取局部最优参数的步骤如下: (1)初始化最优参数。参数变量:k=0.1,λ=1;亮区域最优参数:kmaxl=0.1,λmaxl=1;暗区域最优参数:kmaxd=0.1,λmaxd=1;亮、暗区域的信息熵变量:el=0,ed=0;亮、暗区域最大信息熵:emaxl=0,emaxd=0;参数增量:Δk=0.1,Δλ=1。 (2)求得当前参数下的结果图像。将参数变量k、λ分别代入式(9)和式(10)求得当前参数下的结果图像。 (3)确定结果图像的亮、暗区域。采用Otsu阈值分割算法[29]获取图像的阈值,并依此判断图像的亮、暗区域,将像素值小于阈值的点作为图像暗区域的点,将像素值大于阈值的点作为图像亮区域的点。 (4)计算亮、暗区域的信息熵。通过式(11)分别计算出图像亮区域的信息熵el和暗区域的信息熵ed。 (5)比较信息熵的大小。比较el与emaxl、ed与emaxd的大小。若el>emaxl,则emaxl=el、kmaxl=k、λmaxl=λ。否则emaxl、kmaxl、λmaxl的值保持不变。同理可得到emaxd、kmaxd、λmaxd的值。 (6)根据梯度上升算法增加k和λ的值。设置λ=λ+Δλ、k=k+Δk。重复步骤(2)到步骤(5),直到参数k和λ达到规定的上限为止。此时的参数kmaxl、λmaxl即为使亮区域信息熵取得最大值的亮区域最优参数,kmaxd、λmaxd即为使暗区域信息熵取得最大值的暗区域最优参数。 大量实验表明,最优参数λmaxl、λmaxd的取值以[1,20]为宜。 3.2.3 获取局部最优图像 采用高斯加权双边滤波估计出光照图像后,将3.2.2节求得的局部最优参数kmaxl代入式(9),即可得到未经拉伸的反射图像;将局部最优参数λmaxl代入式(10),即可得到亮区域取得最大信息熵的亮区域最优图像。同理,将参数kmaxd、λmaxd分别代入式(9)和式(10),即可得到暗区域最优图像。 图3显示了对亮、暗区域分别取得最大信息熵时的局部最优图像。其中,图3a为一幅尺寸为400×300的灰度图像,图3b为亮区域最优图像,图3c为暗区域最优图像。图3b中房屋主体等原始图像中明亮区域的增强效果较好,而房前等昏暗区域细节较少;图3c中,房前区域细节增强较好,而房屋主体等原始图像中较为明亮的区域细节丢失。 Figure 3 Original image and local optimal images图3 原始图像和局部最优图像 3.3.1 图像分块融合 为在充分增强图像细节的同时,避免过度增强现象,本文在融合过程中加入原始图像来调节结果图像的亮度。采用分块融合方法对原始图像、亮区域最优图像和暗区域最优图像进行融合处理。 首先,对三幅图像进行相同的分块处理,将图像分为大小相同的方形子块,图像分块示意图如图4所示。假设图像大小为M×N,子块大小为r×r。当图像能够被整分时,区域2和区域3忽略不计,图像被分为(M/r)×(N/r)块;当图像不能被方形子块整分时,将区域2和区域3作为两个独立的子块处理,图像被分为[M/r]×[N/r]+2块([]表示取整函数)。然后,计算每一幅图像的相应子块的信息熵,取相应子块信息熵最大的图像作为该子块区域的选定图像。最后将各选定子块融合,得到高质量的结果图像。在结果图像中,各子块均具有最丰富的细节信息。采用图像分块融合方法对图3中的3幅图像进行融合处理的结果如图5a所示。由图5a可知,在采用分块融合算法得到的结果图像中,图像各子块均取得较好的增强效果,且图像对比度较高。然而,分块图像融合算法存在一个明显的不足,即在融合后的结果图像中,存在严重的块效应。 Figure 4 Schematic diagram of image blocks图4 图像分块示意图 3.3.2 一致性校验 为解决图像融合算法的块效应问题,本节采用一致性校验方法处理融合后的结果图像。 对合成后的图像以子块为单位划分邻域,分别统计每一子块所在邻域内来源于原始图像、亮区域最优图像以及暗区域最优图像的子块个数,并以子块个数为依据对图像进行加权融合。假设在以某子块为中心的邻域内,来源于原始图像的子块个数为no,来源于亮区域最优图像的子块个数为nl,来源于暗区域最优图像的子块个数为nd,则邻域中心子块合成公式如式(2)所示。 f(i,j)=wo×do(i,j)+ wl×dl(i,j)+wd×dd(i,j) (12) 其中,do(i,j)、dl(i,j)、dd(i,j)分别表示原始图像、亮区域最优图像、暗区域最优图像中该子块的像素值,wo、wl、wd分别为原始图像、亮区域最优图像和暗区域最优图像的权重,它们的表达式如下: (13) (14) (15) 图5b显示了采用一致性校验方法处理图5a后的结果图像。由图像可知,一致性校验方法有效地去除了图像的块效应,在块效应去除与图像增强效果之间取得了较好的平衡。 Figure 5 Blocking effect of optimal fusion algorithm and the resulting image of consistency verification图5 图像分块融合的块效应及一致性校验后的结果图像 针对传统单尺度Retinex算法存在的光晕现象,本文采用高斯加权双边滤波估计光照图像,有效去除了光晕现象。针对对比度低、图像泛灰的现象,引入图像融合的思想:首先,以信息熵为衡量标准,通过调整非线性变换的参数得到局部最优图像;然后,采用分块融合算法将原始图像、亮区域最优图像和暗区域最优图像融合成高质量的结果图像;最后,通过一致性校验消除图像分块融合算法产生的块效应,得到图像增强的结果图像。 本文算法的详细流程如图6所示。 Figure 6 Flow chart of the proposed algorith图6 本文算法的流程图 为验证本文算法的增强效果和鲁棒性,分别对两组光照不均匀图像、两组低对比度图像以及两组雾霾图像进行实验,并与三种经典算法和牛为华等人[30]提出的Riemann_Liouville分数阶微分增强算法进行比较。实现工具为Visual C++ 6.0,CPU为因特尔酷睿i5双核2.30 GHz,内存为4 GB,操作系统为Windows 7,64位操作系统。实验中,高斯加权双边滤波的参数:p=5(滤波窗口大小为11×11),γ=20,距离差尺度参数σd=0.01,亮度差尺度参数σl=0.001;图像分块融合的参数:待融合子块大小为5×5,子块邻域大小为31×31。实验结果如图7~图12所示。其中,图7和图8为光照不均匀图像,图9和图10为低对比度图像;图11和图12为雾霾图像。 Figure 7 Enhancement results of non-uniform illumination image House enhanced by five image enhancement algorithms图7 5种图像增强算法对光照不均匀图像House的增强结果 Figure 8 Enhancement results of non-uniform illumination image Girl enhanced by five image enhancement algorithms图8 5种图像增强算法对光照不均匀图像Girl的增强结果 Figure 9 Enhancement results of low-contrast image Birds enhanced by five image enhancement algorithms图9 5种图像增强算法对低对比度图像Birds的增强结果 Figure 10 Enhancement results of low-contrast image Butterfly enhanced by five image enhancement algorithms图10 5种图像增强算法对低对比度图像Butterfly的增强结果 观察图7a和图8a可知,光照不均匀图像亮、暗区域区分明显。亮区域能看到较多细节,暗区域细节丢失严重,几乎看不到细节信息。由于光照不均匀图像的这一特征,在传统算法的结果图像中,亮、暗区域的交界处由于光照对比强烈产生光晕现象,如图7b中树叶边缘和图8b中小女孩头部边缘,增强后图像对比度低、视觉效果泛灰;另外,在均衡图像直方图的过程中,像素个数较少的灰度级被合并到新的灰度级上。因此,直方图均衡算法虽然能够有效提高图像对比度,但存在过度增强以及细节丢失现象,比如图7c中房屋细节丢失,图8c中小女孩脸部过度增强且丢失细节;反锐化掩膜算法通过加强图像边缘轮廓来达到图像增强的目的,而在光照不均匀图像中暗区域细节和轮廓缺失严重,仅加强边缘并不能改善暗区域细节丢失现象。因此,反锐化掩膜算法虽然有效地增强了图像边缘,但对昏暗区域增强效果不显著且图像边缘存在明显光晕现象。如在图7d和图8d中,房屋、小女孩脸部等原始图像中高对比度区域轮廓得到显著增强,但树叶、小女孩的背景区域原始图像中暗区域增强效果微小,且在树叶边缘和小女孩头部边缘光晕现象较明显;Riemann_Liouville分数阶微分算法根据数字图像的自相关性对Riemann_Liouville分数阶微分中常数分数阶不为0的情况进行改进,构建了8个方向的分数阶微分卷积模版,能够提升图像的高频信息。如在图7e和图8e中,高对比度区域增强效果较为明显,但暗区域增强效果不明显。本文算法保留Retinex理论能够消除光照强度对图像影响的优点[31],能够显著增强光照不均匀图像暗区域的细节。此外,高斯加权双边滤波的使用能够有效地克服光晕现象。最后,非线性变换和图像分块融合技术的引用充分考虑了图像的局部最优,极大程度地增强图像的对比度和细节信息,与单尺度Retinex算法相比取得了比较好的视觉效果。 Figure 11 Enhancement results of fog-degraded image Traffic enhanced by five image enhancement algorithms图11 5种图像增强算法对雾霾图像Traffic的增强结果 Figure 12 Enhancement results of fog-degraded image Water Town enhanced by five image enhancement algorithms图12 5种图像增强算法对雾霾图像Water town的增强结果 观察图9a和图10a可知,低对比度图像并不存在区域细节完全缺失的现象,只是图像灰度级分布集中、对比度较低等因素导致图像的细节不明显。从图9和图10两组图像可以发现:由于不存在明暗对比强烈的区域,对于低对比度图像,单尺度Retinex算法的增强结果的光晕现象并不明显,但仍然存在图像泛灰现象;直方图均衡算法、反锐化掩膜算法以及本文算法均能显著地增强低对比度图像,但直方图均衡算法容易丢失细节,比如图9c石头上的细节丢失较多、图10c蝴蝶身体的细节丢失;反锐化掩膜虽然显著地增强了图像的边缘,但对图像亮度改善不明显,增强后的图像亮度与原始图像相似;本文算法使图像的细节得到了显著的增强,同时又改善了图像的亮度,对低对比度图像的增强效果要优于直方图均衡算法和反锐化掩膜算法。 观察图11a和图12a可知,雾霾图像的细节被雾霾遮盖,细节丢失,且视觉效果泛白。观察图11和图12中5种算法对雾霾图像的增强结果可知:单尺度Retinex算法和Riemann_Liouville分数阶微分算法能够增强雾霾图像的细节,但图像泛灰;反锐化掩膜能够增强图像的边缘,但不能改善图像的亮度,且在边缘处存在光晕现象;直方图均衡算法和本文算法均能显著地增强雾霾图像的对比度,但直方图均衡算法存在过度增强和细节丢失现象,比如:图11d中轿车的盖板、图12d的水面等。 通过观察实验的结果图像,我们能够直观地评价不同算法的增强能力,但视觉观察会受到人们主观意识的影响,因此对算法性能的评估还需要客观数据的支持。本文选用均值、标准差、信息熵和平均梯度作为图像增强算法的客观评价指标。 (1)均值。均值被用于评价图像的平均亮度,均值越大,表明图像的平均亮度越大。图像均值的计算公式如下: (16) (2)标准差。标准差被用于评价图像的对比度,标准差越大,表明图像的对比度越高,图像视觉效果越好。标准差的计算公式如下: (17) 其中,mean表示图像像素的平均值。 (3)信息熵。信息熵被用于评价图像所包含信息的丰富程度,信息熵越大表明图像的细节信息越丰富,算法的增强效果越好。图像信息熵的计算公式如上文式(11)所示。 (4)平均梯度。平均梯度被用于评价图像的清晰度,平均梯度越高,表明图像的清晰度越高,图像视觉效果越好。图像平均梯度的计算公式如下: f(i+1,j))2+(f(i,j)-f(i,j+1))2))1/2 (18) 5种算法对光照不均匀图像、低对比度图像和雾霾图像的增强结果的客观数据比较情况分别如表1~表3所示。 由表中数据可知:在均值方面,除反锐化掩膜外,其他4种图像增强算法对光照不均匀图像和低对比度图像的增强结果的均值都有所提升,对雾霾图像的结果图像的均值都有所下降。这是因为雾霾图像的细节被雾霾遮盖,具有整体泛白的特征,原始图像的均值较大,而在增强雾霾图像的过程中,图像的对比度得到增强,去除了雾霾对图像的细节的遮盖,这会导致图像均值下降。雾霾图像增强后的结果图像的均值在一定程度上的下降恰恰说明增强效果显著。同样,反锐化掩膜算法的结果图像的均值与原始图像接近,结果图像亮度改善程度较小。 Table 1 Result comparison of non-uniform illumination images among the five algorithms表1 5种算法对光照不均匀图像的增强结果的客观数据对比情况 Table 2 Result comparison of low-contrast images among the five algorithms表2 5种算法对低对比度图像的增强结果的客观数据对比情况 Table 3 Result comparison of fog-degraded images among the five algorithms表3 5种算法对雾霾图像的增强结果的客观数据对比情况 在标准差方面,对于这3种类型的图像,使用单尺度Retinex算法进行增强,其结果图像的标准差均较低,图像泛灰。反锐化掩膜算法对光照不均匀图像的增强结果的标准差较高,对低对比度图像和雾霾图像的增强结果的标准差略低。直方图均衡算法、Riemann_Liouville分数阶微分算法和本文算法对3种类型图像的增强结果的标准差均较高,结果图像对比度高。 在信息熵方面,对于这3种类型的图像,使用直方图均衡算法进行增强,其结果图像的信息熵均下降,图像细节信息丢失。反锐化掩膜算法由于对图像暗区域增强效果微弱,因此对光照不均匀的图像进行增强,其结果的信息熵下降。Riemann_Liouville分数阶微分算法相对于其他算法均值较高但信息熵较低。本文算法产生的增强结果的信息熵均远大于其他4种算法,结果图像的细节信息丰富。 在平均梯度方面,对于这3种类型的图像,使用这5种图像增强的算法进行增强,其结果图像的平均梯度均有所提升,图像的清晰度得到了增强。其中,反锐化掩膜算法、Riemann_Liouville分数阶微分算法和本文算法的清晰度提升程度高于其他2种算法。 综上所述,单尺度Retinex算法适用于增强光照不均匀的图像,但存在光晕现象和泛灰问题;直方图均衡算法虽然能够显著地增强图像的对比度,但细节丢失的现象严重;反锐化掩膜算法适用于增强低对比度的图像,对光照不均匀的图像和雾霾图像中缺失的细节增强效果不显著;Riemann_Liouville分数阶微分算法对图像的高对比度信息进行了有效提升,但对光线昏暗且对比度较低的信息和雾霾图像的增强效果不明显;综合结果图像和客观数据来看,本文算法无论对光照不均匀的图像、低对比度图像还是雾霾图像均有比较好的增强效果,在图像增强能力和鲁棒性等方面均优于其他4种算法。 针对传统单尺度Retinex算法存在的光晕现象和泛灰问题,本文提出了一种新的基于图像融合技术的Retinex图像增强算法。首先,采用高斯加权双边滤波估计光照图像,去除了单尺度Retinex算法的光晕现象。然后,通过调整非线性变换的参数得到局部最优图像。最后,采用图像分块融合技术将原始图像和局部最优图像融合成高质量的结果图像,并采用一致性校验的方法去除分块融合产生的块效应。对本文算法以及上述4种图像增强算法进行了对比实验,结果表明,本文算法对实际应用中常见的光照不均匀的图像、低对比度的图像以及雾霾图像均取得了较好的增强效果,具有较强的图像增强能力和鲁棒性。但实际应用中还会有相对恶劣的环境,如强光背景下小目标与背景灰度接近,目标与背景难以区分,因此对于本文算法来说,对强光背景下小目标的增强,还有待提高。下一步将对如何根据图像特征自适应地确定分块融合中待融合子块的大小以及一致性校验中子块邻域的大小进行研究。3.2 局部最优图像的获取




3.3 图像融合

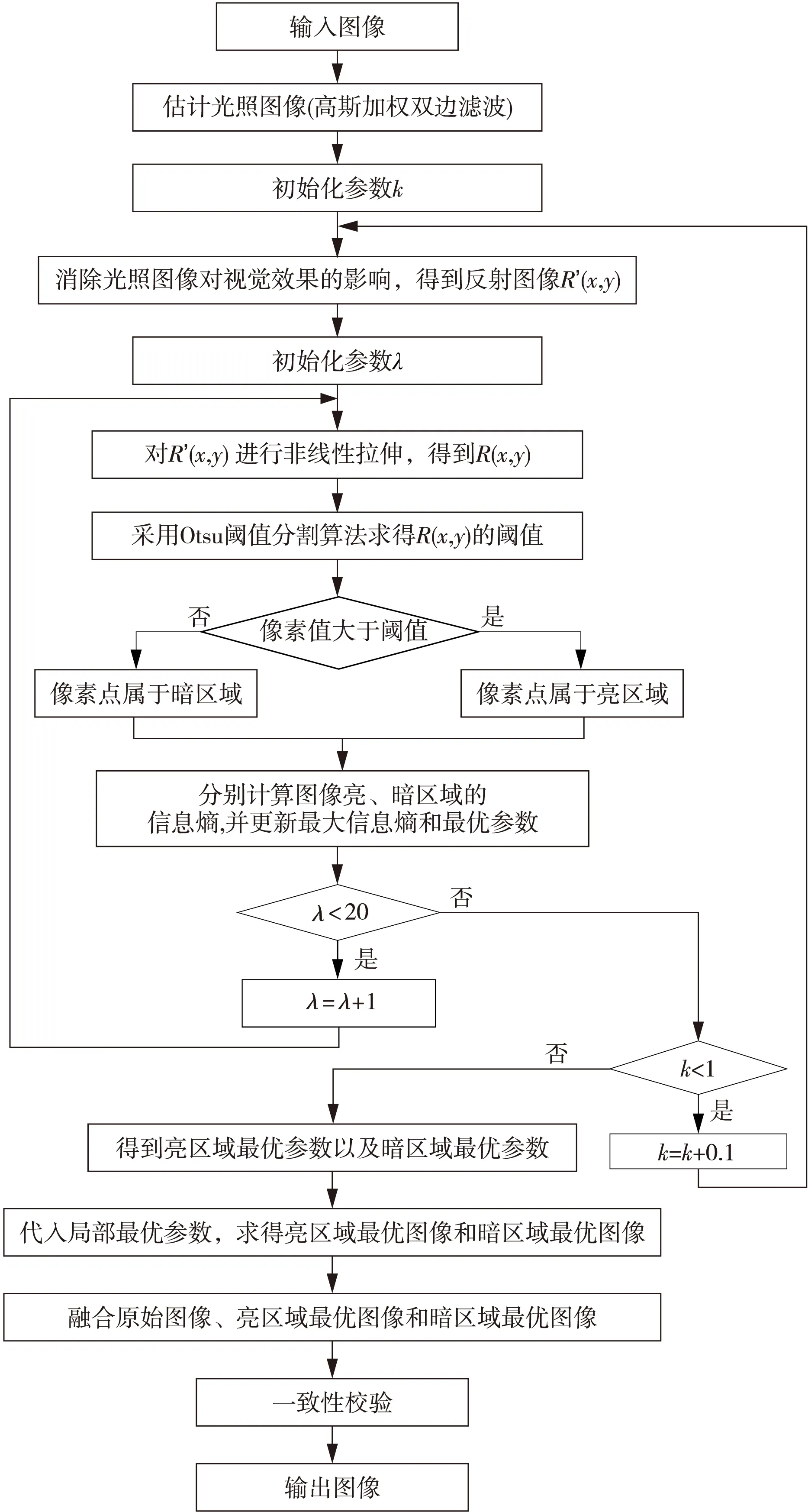
3.4 算法总体框架
4 实验结果分析







5 结束语

