一种适用于微波无线输能系统的自聚焦控制算法优化实现

程晓洁，卢毅，彭革新

（中国电子科技集团公司第七研究所，广东 广州 510310）

1 引言

微波无线输能技术（MPT, Microwave Power Transmission）[1-3]源自空间太阳能电站设想，是指将直流电能转换为微波，并通过自由空间进行传播，在到达接收部分后再次转化为直流电能。该技术可以实现设备无缆化，是供能系统的颠覆性技术，引起了国内外的广泛研究。微波无线输能技术除应用于空间太阳能电站系统外，还可以应用于临近空间飞行器、空中通信中继站、卫星电力中继、恶劣环境的电力供应等领域，应用前景广泛。

根据空间功率合成技术原理[4]，当所有同频发射信号在接收点处同相叠加时，合成的场强达到最大值，此时，接收点处的合成场强为单个发射单元场强的N倍，接收天线的入射功率为单个单元入射功率的N2倍，若接收点处各发射信号不同相，则其幅度有可能相互抵消，损失能量。微波无线输能系统中的波束聚焦即是采用了空间功率合成技术，发射端天线阵列单元辐射的相位差异决定了波束合成和波束指向，会影响系统的效率。因此必须进行波束控制算法设计，通过调整发射端天线阵元的相位，使得到达接收面聚焦点的场强最大，提升接收功率，从而提高无线能量传输的效率。传统的相位控制算法有链路补偿法，反向导引[5]、反向天线阵（Retrodirective）等设计。链路补偿法需要所有发射天线共源，线缆长度一样，形成预想的波束，然后计算移相器的相移，该种方法需要大量的计算，温度、线缆等其他干扰因素很多，校正方法复杂，针对移动目标时每个天线都要大量的计算。反向导引和反向天线阵需要目标携带一个信标，根据信标发射的导引信号，计算路径的相位，进而根据计算的相位发射主信号，该算法需要每个发射单元都配置接收机，系统庞大。

本文基于MPT系统工程化设计的需求，优化实现了一种自聚焦控制算法，利用接收端实测的场强幅度差计算每个发射天线阵列单元与其它天线合成场的相位差，进而反馈控制发射单元的相位，多次迭代后所有的天线单元到达接收端的相位都同步，接收点的场强幅度和功率最大。

2 自聚焦控制算法设计

本文提出了一种针对微波无线输能系统的自聚焦控制技术[6]的改进算法，在将±90°相位调制后形成的功率差进行反馈的基础上，增加了0°和180°相位调制形成功率差的反馈[7]，避免了算法中对特殊值解的不适用性，同时弥补了所得调相值解的局限性，进而根据调相值控制发射端信号的相位，使得所有的发射信号在聚焦点同相，合成场强最大。

改进后的控制算法原理如图1所示，Q表示任意一个发射单元场强矢量，R表示其它N个单元的合成场强矢量，将Q信号进行±90°超前和滞后相位调制，分别得到Q1和Q2矢量，Q1和Q2分别与R合成R1和R2矢量，计算R1和R2的矢量幅度差；再将Q信号进行0°和180°相位调制，分别与R合成得到R3和R4矢量，计算R3和R4的矢量幅度差。

各信号矢量方程如下：

图1 改进后的控制算法原理

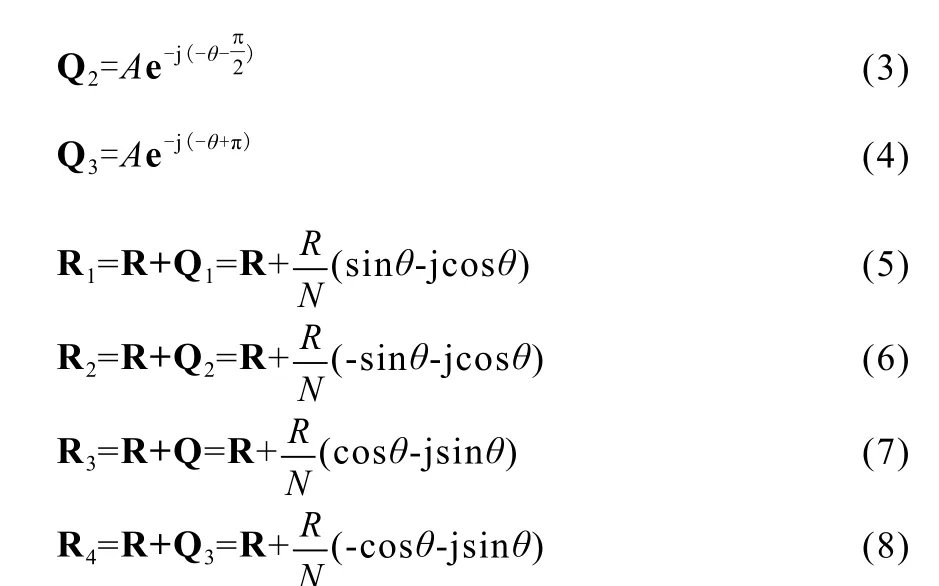
其中：A表示任意发射单元的信号幅度；N表示其它发射单元数量。假设各个发射单元的场强幅度都相等，则R=NA。

若Q和R信号矢量存在θ相位差，则R1和R2幅度、R3和R4幅度必然存在差异，幅度差方程如下所示：

将公式(9)和公式(10)相除，可得：

根据公式(11)可得，相位差θ可以通过检测±90°调制后的幅度差值和0°、180°调制后的幅度差值计算得到，不需要测量R的幅度值。

通过调整Q信号的相位，使得R1和R2的幅度差为0，则认为Q信号与主波信号R在接收点处同相，即相位差θ=0。依次轮流调整其它发射单元的相位，使得所有发射单元在接收点处同相，则发射波束在接收点处聚焦，场强最大，接收功率最大。

公式(11)在|R4|=|R3|时，tgθ=0，θ存在特殊值，因此由公式(9)和公式(10)继续推导，可得：

将公式(12)代入公式(13)可得：

由公式(13)计算相位差θ时，不会出现特殊值，比公式(11)更适合实际实现。

但仅通过该公式得到的相位差在-π/2～+π/2之间，故当相位差θ在+π/2～3π/2之间时，文献[7]的算法无法求得准确的相位差值。

本算法提出了根据公式(10)计算得到的cosθ值用于判断相位差的区间，当cosθ＞0时，相位差θ在-π/2～+π/2之间；当cosθ＜0时，相位差θ在+π/2～3π/2之间，此时，

3 仿真设计及结果分析

采用Matlab软件对优化后的自聚焦控制算法进行了建模仿真，模型设计为4点阵，将4个发射点和4个接收点在三维坐标上分别标示各点坐标，P为接收面上任意一点，Φ为相对于口径法线的角度。采用矢量矩阵法计算接收面上任意点的场强大小，利用软件计算和绘制三维归一化功率密度图，通过调整相位，得到中心聚焦的功率密度分布。计算模型中变量参数为工作频率f、收发间距L、天线口径D、天线间距d。算法计算模型如图2所示。

根据矢量余弦函数：

可以得到φAi的值，该值为收发天线间距L和发射天线间距d的函数。

将φAi值代入归一化场强函数[8]：

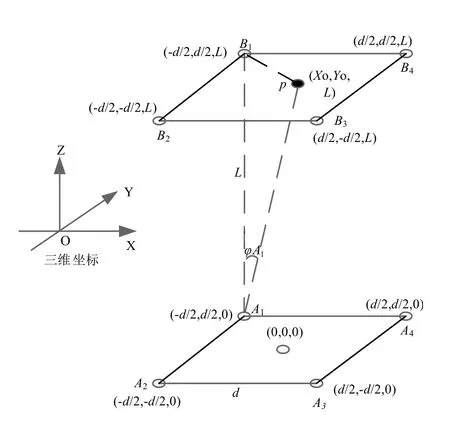
图2 算法模型示意图

其中，D为发射天线口径直径，单位为m；λ为波长，单位为m；φ为相对于口径法线的角度；J1为一阶贝塞尔函数。

可以得到任一发射天线Ai在接收面上任意一点P处的归一化场强大小EAip(φAi)。

各发射天线到P点处的相位由初始相位θi0和行程组成。任一发射天线Ai到达P点处的相位为：

则各点到达接收面P点的场强为：

P点处的合成场强为：

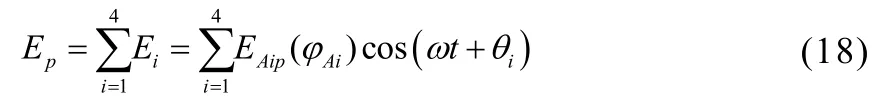
场强幅度值为：

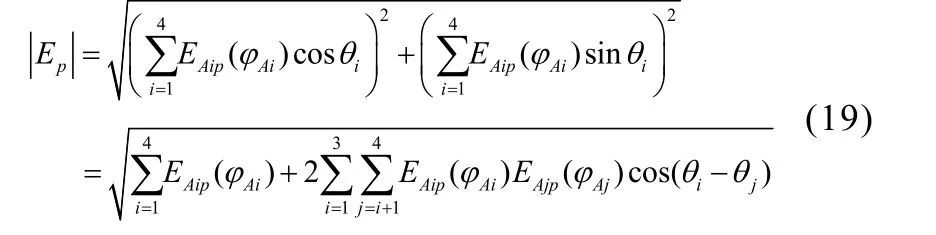
由该公式推导可见，当各发射天线到达P点处的相位θi都相等时，该点的场强最大，为各发射天线的场强幅度之和，即相应的功率密度也最大。

根据上面的运算模型，运用Matlab软件进行计算，得到算法仿真结果，如图3所示。某一次天线调整完毕后，移相角度在6次迭代调整后逐渐趋向于0°，表示相位同步，不再移相；接收点天线场强幅值从小变化到大，在移相角度趋于0°后达到最大值并稳定，算法收敛；天线角度方差表示几个发射信号到达接收点处的相位方差值，算法收敛后，相位方差值趋于0。

算法仿真一次迭代计算时间小于4.82 ms，5次迭代总时间约为24.1 ms，算法仿真收敛速度较快。

算法计算同时利用工具进行三维图形描绘，可以得到功率密度分布波形，如图4所示。

图3 算法仿真结果

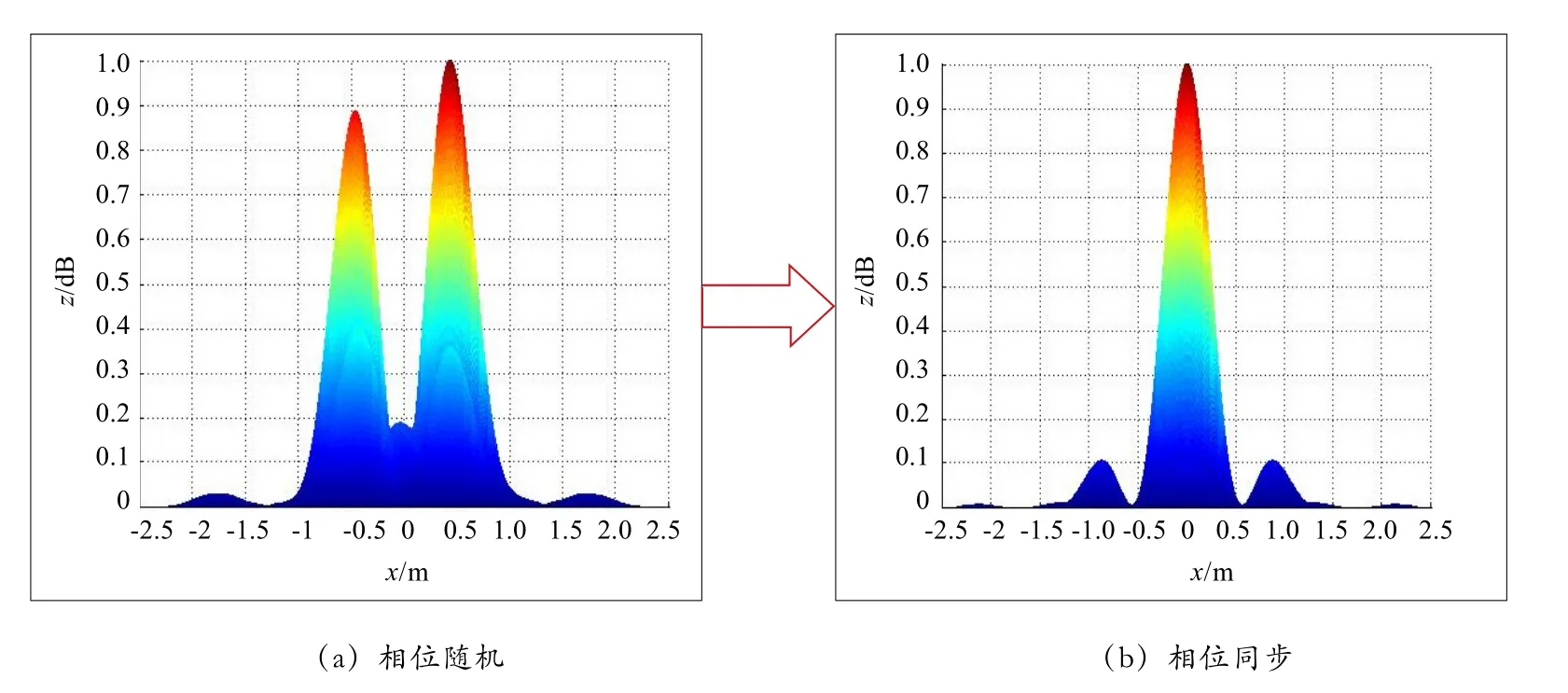
图4 功率密度仿真分布图

由图4可见，初始发射信号相位随机时，接收面上的场强幅度有增强，也有抵消，形状分散，通过算法计算调整迭代后，到达接收面某一点的各信号相位同步，该点场强幅度最大，接收到的功率也最大，实现聚焦。仿真结果证明了该自聚焦控制算法的正确性和可行性。

4 验证实验

基于该算法及仿真结果，设计了自聚焦控制验证系统进行了实验验证，实物验证系统如图5所示。系统分为接收天线阵面、接收控制部分、发射天线阵、发射端功放及调制移相控制系统、数据处理/控制/显示终端等，工作原理如图6所示。发射天线阵采用2×2抛物面天线，天线口径为0.2 m，工作频率为11.2 GHz，功率放大器功率为20 W，移相器为6位移相器；接收天线阵面采用8×8微带天线阵列；数据处理/控制/显示界面可以控制功放开关、实时查看各个接收天线接收到的功率值、算法开关、计时记录及过程曲线绘制。

在实测过程中，发现算法在初始两轮迭代中相位差计算精度较高，移相效果好，在接收面聚焦点能达到场强最大值；两次迭代以后，由于6位移相器的移相误差、算法计算转换误差等因素，导致多次迭代后会出现震荡，相位误差反而变大，中心场强幅值减小，对实测数据影响较大。为了优化算法实际运行的鲁棒性，在粗调后的迭代过程中增加了微调算法，避免了中心场强幅值的震荡，使得算法更具有实用性。

图5 验证系统实物图

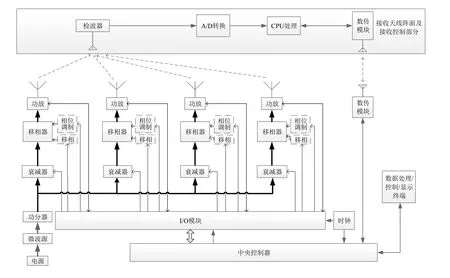
图6 验证系统工作原理图

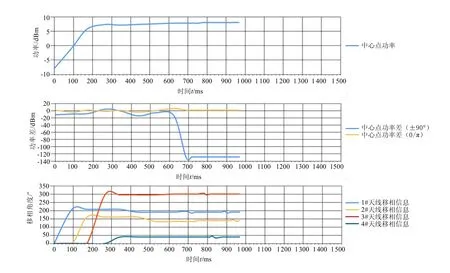
图7 验证系统实测数据

验证系统某次实测数据如图7所示，分别列示了中心点功率曲线、±90°调制后的中心点功率差和0°/180°调制后的中心点功率差、4根天线的移相信息。由图中可见，中心点功率值随着4根天线的移相，逐渐增大，最终达到稳定值；中心点功率值达到稳定后，±90°调制后的中心点功率差值非常小，说明此时被调天线和其余天线的合成主波之间的相位差非常的小，不需要再调整了，相反的，相位差很小的情况下，0°/180°调制后的中心点功率差值达到最大。4根天线依次调相，几轮迭代后各天线相位小幅度调整，逐渐趋于稳定，由图中横轴可见，本次算法运行时间约为980 ms。实测数据进一步验证了自聚焦控制算法的正确性和可行性。

验证实验设置了三个平行的聚焦点，每个聚焦点间距为0.25 m，用于验证算法适用于移动目标的可行性。三个聚焦点实测数据对比如表1所示：

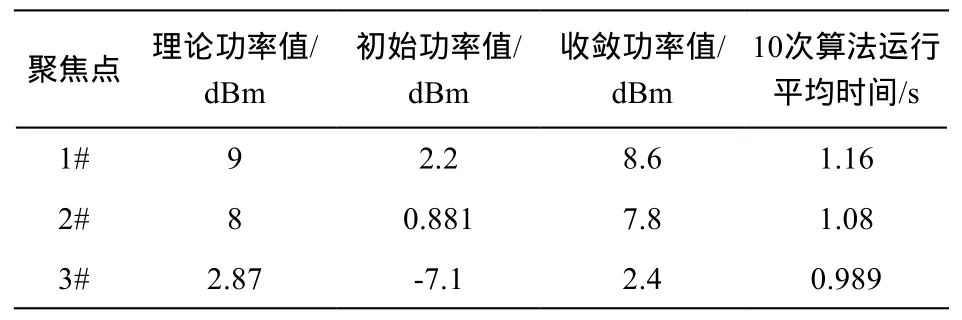
表1 不同聚焦点实测数据对比

由表1可见，实测收敛功率值与理论计算功率值差异不大，随着聚焦点距离变远，每个发射天线到达聚焦点的波束方向与天线口径法线之间的夹角变大，即波束角变大，因此聚焦后的场强幅值变小，但由显示界面实时观测，相对于周边来说，该点的场强幅值最大，实现了在该点聚焦。由对比测试可知，该算法可跟踪目标实现能量聚焦，若发射天线安装伺服机构，则可精确随动地对准聚焦点，始终保持聚焦点处功率最大。

该算法运行时间与天线的初始相位无关，仿真收敛时间为24.1 ms，但实测收敛时间约为1 s，时间较长，经分析，存在以下几个原因：（1）本验证实验以验证算法收敛性为主，未严格执行时序控制，每个天线分配的时间过长；（2）算法由粗调转为细调时，收敛后还延时了四次运算进行误差分析；（3）算法本身运算时间很快，但验证时受限于工程实施上的硬件传输延时和图形数据显示转换延时，导致实际显示的时间较长。针对这几个原因，可以通过设置精确的时序控制、提高硬件的配置和简化图形显示，进一步改进缩短算法收敛的时间。该算法在针对移动目标实际应用时，会跟随目标实时持续运算，保证能量在目标物上一直聚焦，算法运算速度的提升可以更好地适用速度更快的移动目标物的微波无线输能，支撑该目标物的功能作用。

5 结论

本文针对自聚焦控制算法进行了理论优化，避免了算法中对特殊值解的不适用性，同时弥补了所得调相值解的局限性，在工程实现中，进行了算法的鲁棒性优化，避免了接收点的功率震荡，使其更加稳定。对优化后算法的仿真和实测结果证明：（1）该算法适用于MPT系统的工程化应用，相位同步收敛快，自动聚焦精确且聚焦点功率稳定；（2）通过进一步提升硬件性能和优化算法运行速度，可以适用于移动目标的聚焦控制。将该算法应用于MPT系统中，可以提升系统的捕获效率，进而提高整体效率，推动微波无线输能技术的实用化发展。