基于EKF的实时循环神经网络在非定常气动力建模中的应用

付军泉, 史志伟, 陈 坤, 朱佳晨, 陈 杰, 董益章

(南京航空航天大学 航空宇航学院, 江苏 南京 210016)

0 引 言

飞机在大迎角过失速机动飞行时，气动力具有非定常和非线性的特性，而非线性、非定常气动力的预测，对新一代战斗机设计具有十分重要的意义。随着人工智能技术的发展，神经网络在非线性系统辨识中得到了一定应用，如径向基神经网络[1]、模糊神经网络[2]和自适应神经网络[3]。但这些网络本质上都是前向的静态网络，并不能很好的反映系统的动态特性。而循环神经网络是一种具有反馈结构的神经网络，可以反映系统随时间变化的动态特性，并且可以储存信息。网络的输出不仅与当前的网络输入和权值有关，还与网络之前的输入有关，从而可以表现出非线性系统的动态特性。循环神经网络在非线性系统辨识中已得到应用[4-6],能够对大部分非线性系统进行建模，但找到一种权值修正的方法使其收敛到有效的模型仍是一个亟待解决的问题。

EKF算法具有较快的收敛速度，但是收敛精度

不高[7],已经被用在循环神经网络[8]，而实时递归学习算法[9]作为一种在线训练算法，对于样本数据可以进行不断的学习，在每一时间节点都对网络权值进行调整，对复杂非线性问题的处理具有一定优势，能更精确的模拟非线性系统的动态特性，但是其计算量大，训练速度较慢[10]。

本文采用循环神经网络，结合EKF和实时递归学习算法的特点，提出一种基于EKF的实时递归学习算法，该算法既具有较快的收敛速度又具有较高的收敛精度, 十分适合于非线性动力学系统的辨识。文中给出了循环神经网络在应用此学习算法下的仿真结果，验证了本文所提算法的有效性。

1 循环神经网络

本文中循环神经网络是一种全联接的Elman网络[11]，一般由输入层、隐含层、关联层和输出层组成，如图1。

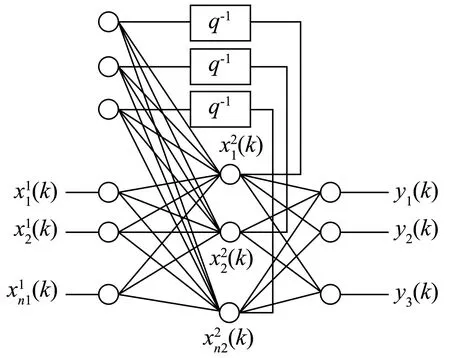
图1 循环神经网络结构Fig.1 The structure of RNN

第一层是输入层，输入层中的第i个节点的输入为:

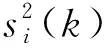
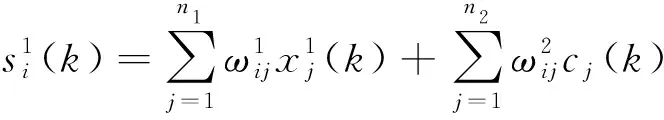
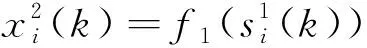
关联层的输入为隐含层上一时刻的输出，输出等于输入，其第i个节点的输入输出分别为

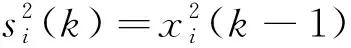
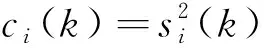
第三层为输出层，其第i个节点的输入输出分别为：

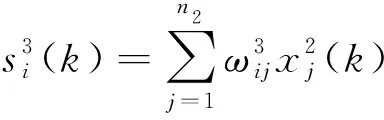
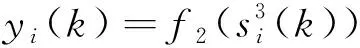
2 基于EKF的实时递归学习算法

实时递归学习算法是一种基于梯度下降法的学习算法，属于在线学习，对k时刻的网络误差函数进行定义：

e(k)=yd(k)-y(k)(9)

yd(k)为k时刻的期望输出，e(k)即为k时刻期望输出与网络实际输出之间的误差。则网络权值修正的误差梯度为：

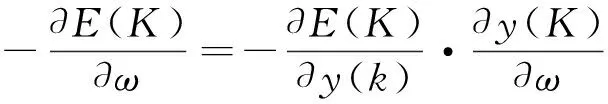
ω可表示输入层、隐含层和输出层的权值。实时递归学习算法在每一时间节点都通过误差梯度对网络权值进行修正，是一种实时计算，计算量极大。本文引入扩展卡尔曼滤波计算网络权值误差协方差矩阵P，每次计算只保留卡尔曼增益K和误差协方差矩阵P,用来对网络权值进行修正，因此网络的运行速度很快，可以很好的解决实时计算带来的计算量大的问题。对网络权值的变化由文献[12]确定：

ω(k)=ω(k-1)+Δω(11)

ω(k)不仅与k时刻的期望值和网络输出值之间的误差有关，还与上一时刻的网络权值有关，其学习过程根据文献[13]进行：

K(k)=P(k-1)HT(k)·

[H(k)P(k-1)HT(k)+R(k)]-1(12)

Δω=Ke(k)(13)

P(k)=P(k-1)-K(k)H(k)P(k-1)+Q(k)(14)

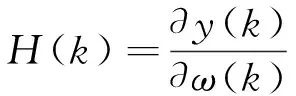
其中，Q(k)为网络噪声的协方差矩阵，R(k)为实验噪声的协方差矩阵。K时刻网络权值的修正值Δω由此时的卡尔曼增益K(k)和误差e(k)求得，接下来对该时刻的误差协方差矩阵P(k)进行更新，以便用到对下一时刻的网络权值的预测。由此不断把误差协方差矩阵进行递归，每一次运算都只保留上一时刻的P，如此自回归运算下去，使得网络运行速度快。H可由网络误差梯度确定。

对于输出层：

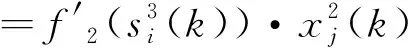
隐含层：

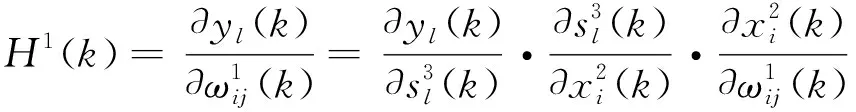
同理，关联层：

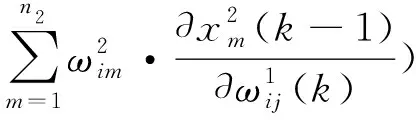
在EKF-RTRL学习算法中，网络噪声协方差矩阵Q(k)、实验噪声协方差矩阵R(k)、网络权值误差协方差矩阵初始值P(1)对算法收敛性是有影响的。根据参考文献[14]，初始方差矩阵P(1)对滤波效果影响很小，算法都能较快收敛，所以P(1)可以任意取一个不为零的矩阵，本文中P(1)取为单位对角阵。网络噪声协方差矩阵对结果误差影响较大，随着Q(K)增大而增大，变换较为显著。所以网络噪声协方差矩阵的取值越小越好，可以使用一个很小但不为零的矩阵，本文取Q(K)=10-4×diag([1,1])。实验噪声协方差矩阵R(K)的取值变大或变小，效果不一定好，在计算时进行了多次的选值调整，使结果最好。

3 算例

3.1 风洞试验

本文实验动态机构如图2，由支撑机构、振荡机构、运动控制机构和数据采集系统组成。支撑机构运动由计算机通过液压传动机构控制，可按任意规律变化。该机构可以实现偏航、滚转以及偏航滚转耦合运动。③和⑧分别是模型偏航角φ和滚转角φ的角度编码器。可测量模型运动的偏航角和滚转角。模型迎角θ人工测量。

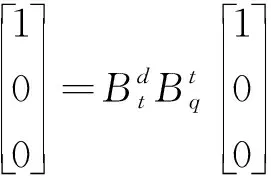
可得迎角α和侧滑角β：

sinβ=sinθsinφcosφ+sinφcosφ(20)

该实验在南京航空航天大学NH-2低速风洞进行。

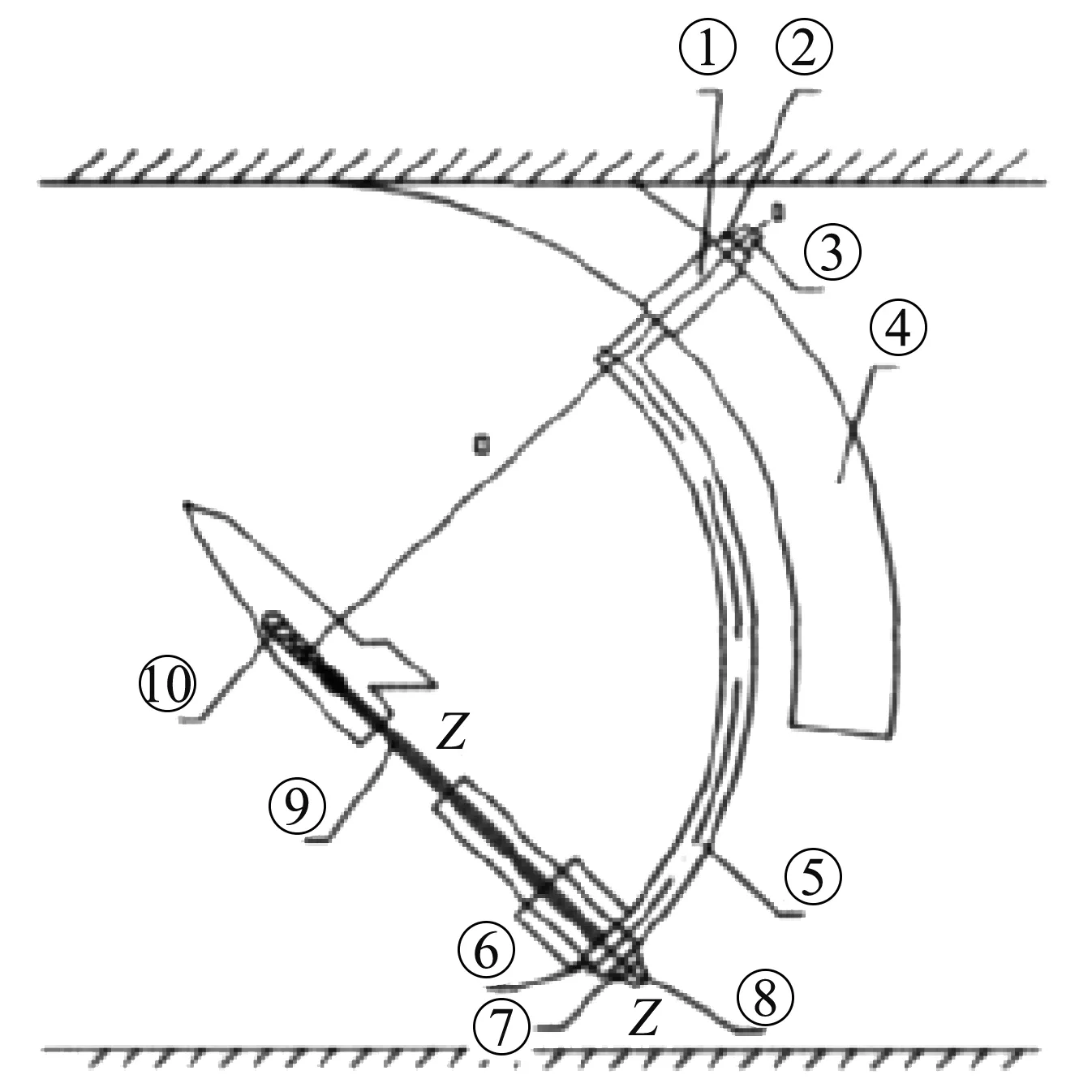
图2 动态试验机构Fig.2 Dynamic testing mechanism

3.2 建模数据

该神经网络的建模数据来自于某飞机模型支撑迎角为50°时，不同振动频率下的大振幅动态实验数据，包括单自由度的偏航、滚转运动和两自由度的偏航滚转耦合运动。其中单自由度偏航和两自由度偏航滚转耦合运动的动态实验频率为0.2、0.4、0.6、0.8，将0.2、0.4和0.8三组数据作为训练样本进行建模，0.6频率数据作为模型仿真验证；单独滚转运动的动态实验频率为0.4、0.8、1.2、1.6，将0.4、0.8、1.6三组数据作为训练样本进行建模，1.2频率数据作为模型的仿真验证。

本文实验数据较多，数据跨度较大，各变量间的量级相差较大，为了使实验数据跨度缩小，便于建模仿真，对实验数据进行了归一化处理，将其处理为[-1，1]之间的数据，采用如下公式：

3.3 建模和验证

本文在运用循环神经网络对非定常气动力建模时，将单自由度偏航、滚转以及偏航滚转耦合运动数据放在一起进行网络训练，建立统一的模型，对于横航向运动，主要考虑其滚转力矩系数和偏航力矩系数，具体模型为：

Mx=F(β,p,r,f)，My=F(β,p,r,f)，其中p为滚转角速度，r为偏航角速度，f为振动频率。

对于单自由度偏航运动，f=0.4的实验数据在建模时已经作为训练样本使用，图3是建模结束后，使用建立好的神经网络模型重新对此频率数据进行仿真的结果。图4是建模时未使用的f=0.6的实验数据在此神经网络模型下的仿真预测结果。对于单自由度的滚转运动，图5、图6为仿真结果与仿真预测结果同实验结果的比较。对于两自由度的偏航滚转耦合运动，图7、图8为仿真结果与仿真预测结果同实验结果的比较。

由以上各对比结果图可以看出，不管是对训练时使用过的数据进行仿真，还是用训练时未使用过的数据进行仿真预测，其得到的偏航力矩系数和滚转力矩

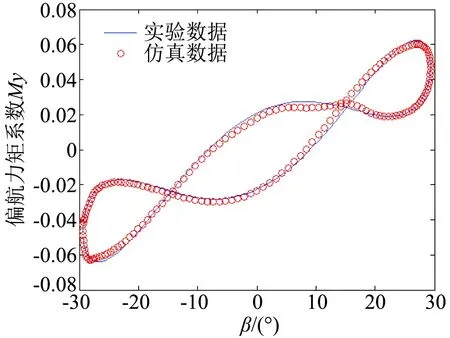
图3 偏航运动仿真结果与实验结果对比(f=0.4)Fig.3 The comparison between the simulation results and the testing results in yaw motion (f=0.4)

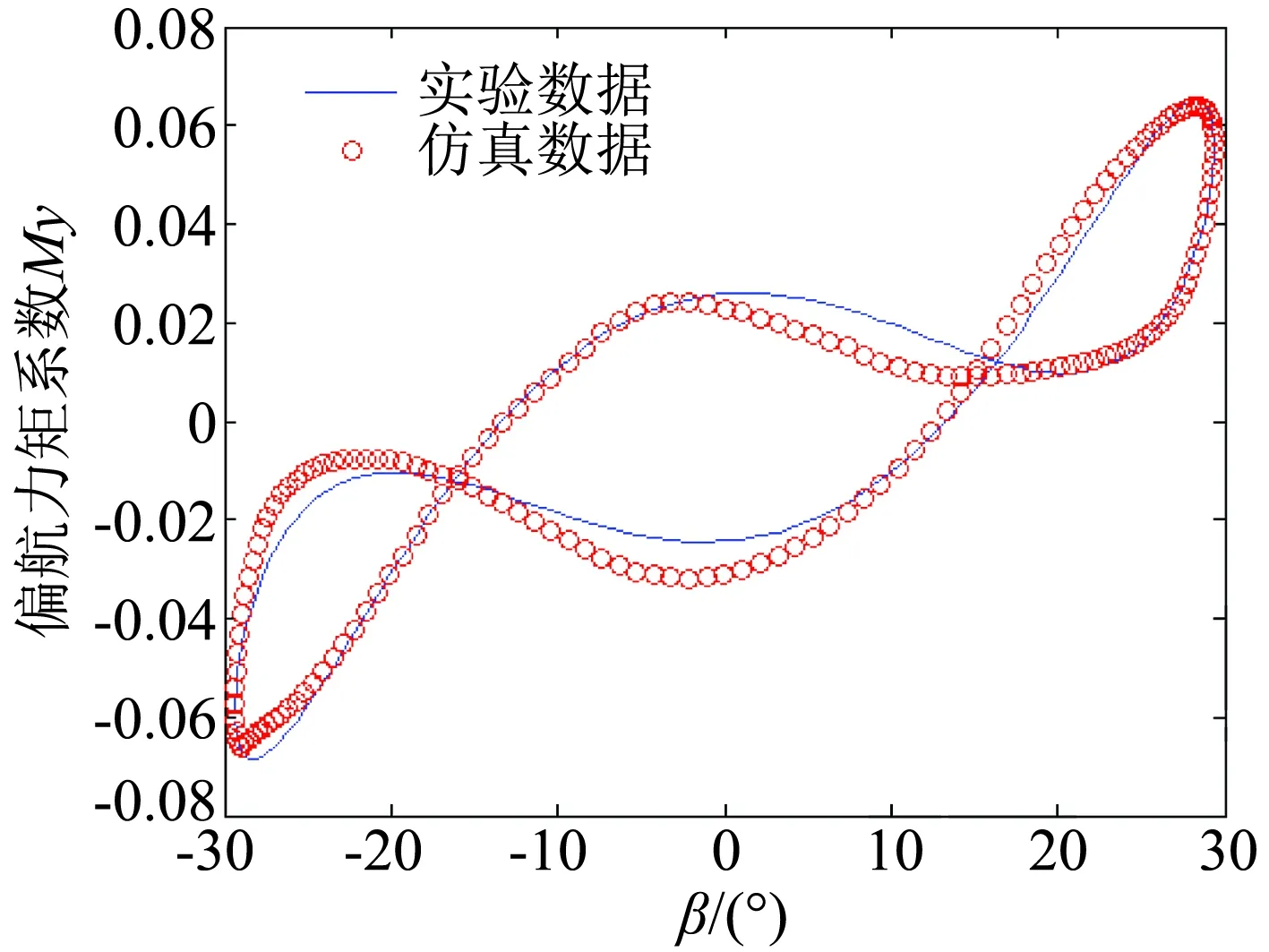
图4 偏航运动仿真预测结果与实验结果对比(f=0.6)Fig.4 The comparison between the simulation prediction results and the testing results in yaw motion (f=0.6)

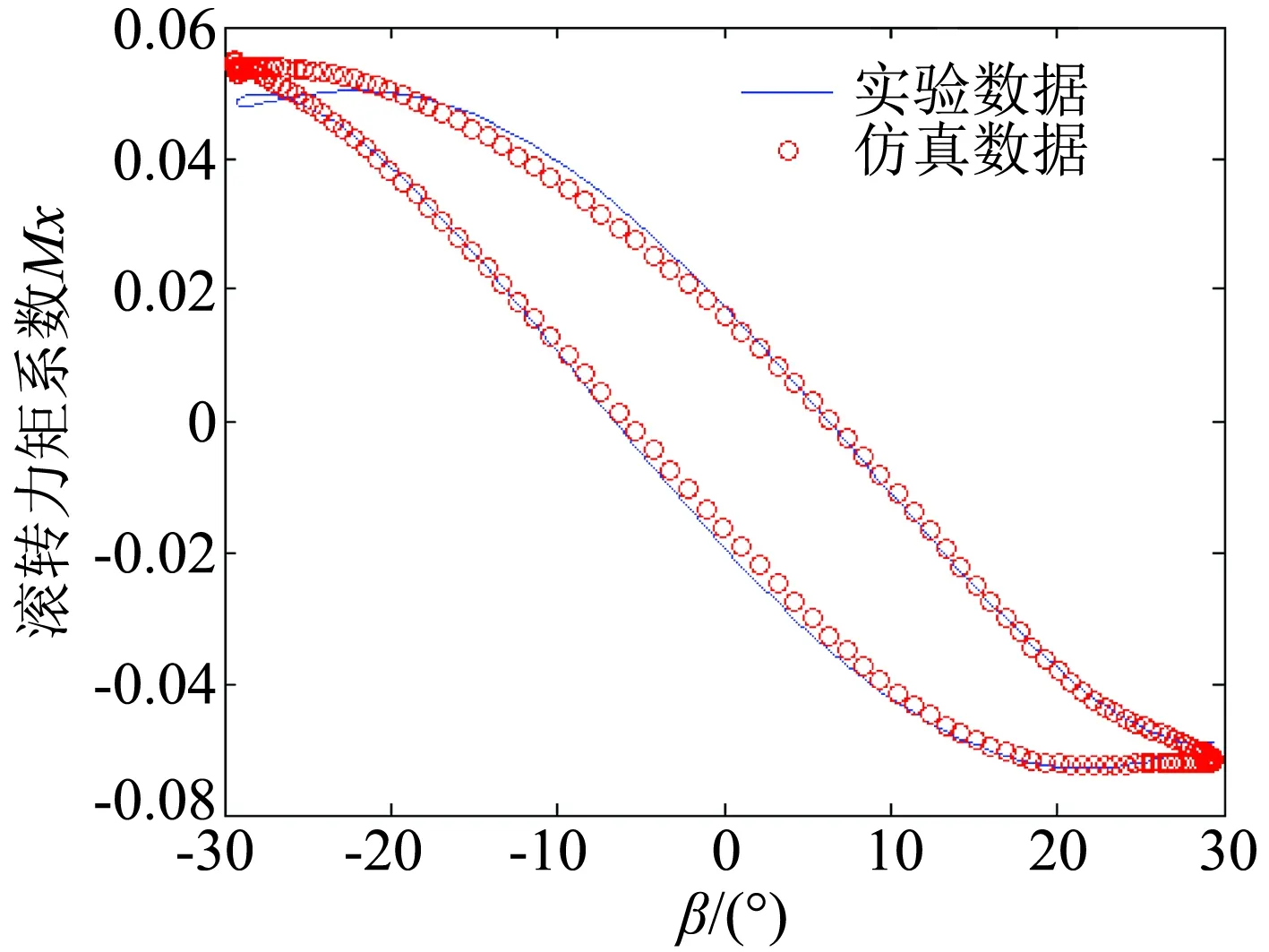
图5 滚转运动仿真结果与实验结果对比(f=0.8)Fig.5 The comparison between the simulation results and the testing results in roll motion (f=0.8)

系数与实验所得的数据都几乎重合，这充分证明了该神经网络模型在非定常气动力建模上的可行性。

本文建模采用大振幅动态数据，得到了很好的结果，为进一步验证该神经网络模型适用性，将大振幅下建立好的模型运用到对小振幅数据的仿真预测。图9、图10分别是小振幅单独偏航(f=0.4)、滚转(f=0.8)运动的仿真预测结果和实验结果的对比。

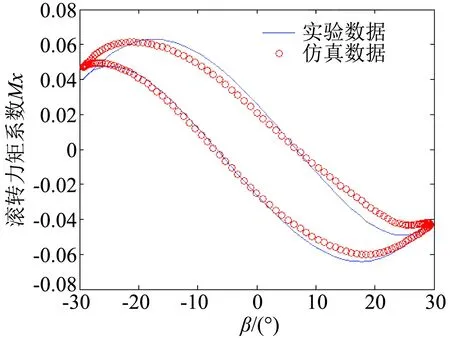
图6 滚转运动仿真预测结果与实验结果对比(f=1.2)Fig.6 The comparison between the simulation prediction results and the testing results in roll motion (f=1.2)

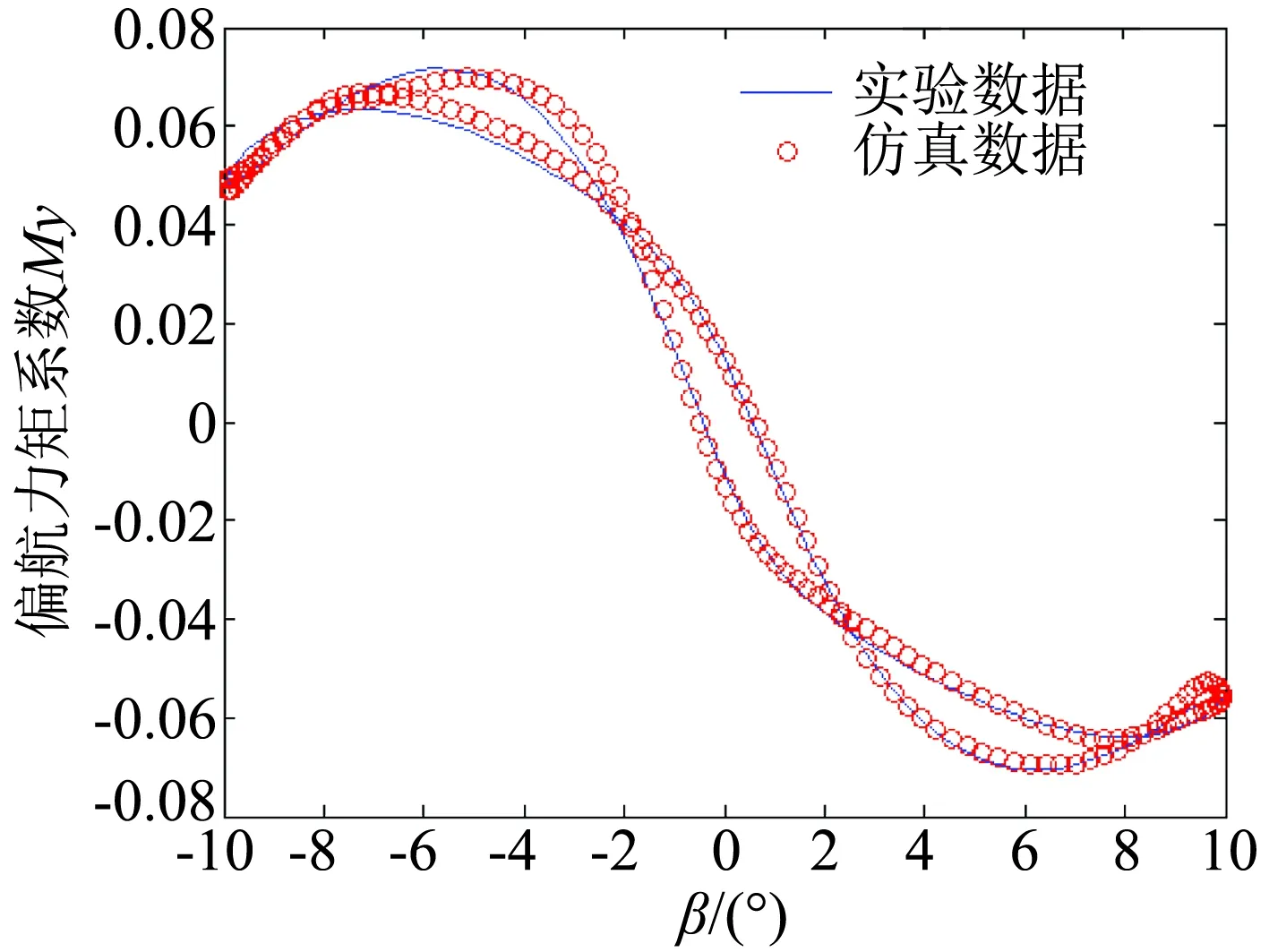
图7 偏航滚转耦合运动仿真结果与实验结果对比(f=0.4)Fig.7 The comparison between the simulation results and the testing results in yaw-roll motion (f=0.4)

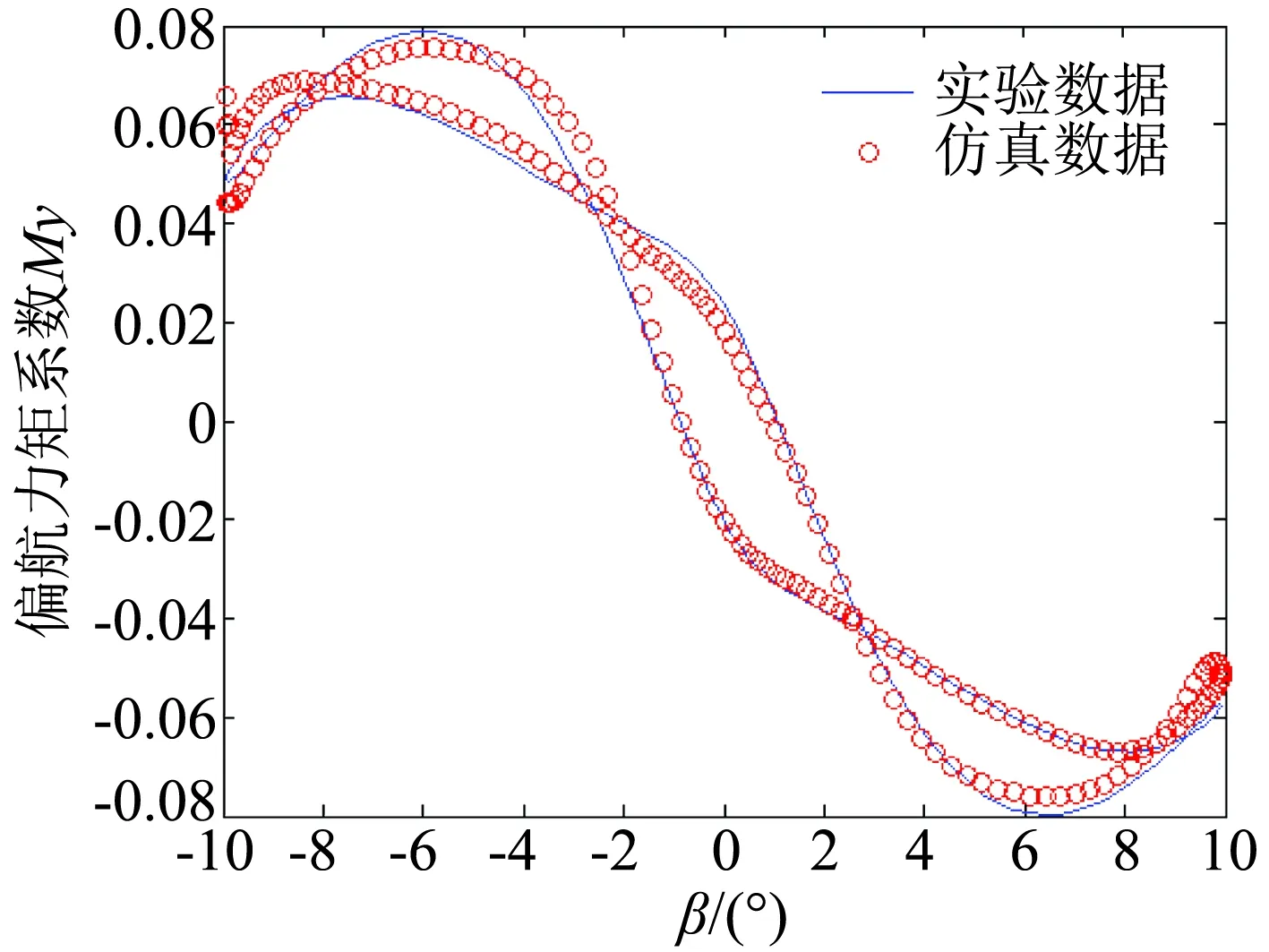
图8 偏航滚转耦合运动仿真预测结果与实验结果对比(f=0.6)Fig.8 The comparison between the simulation prediction results and the testing results in yaw-roll motion (f=0.6)

由图9和图10可以看出，小振幅下实验结果和仿真预测结果的拟合程度较好，说明用大振幅数据建立的神经网络模型在小振幅情况下可以较好的适用。

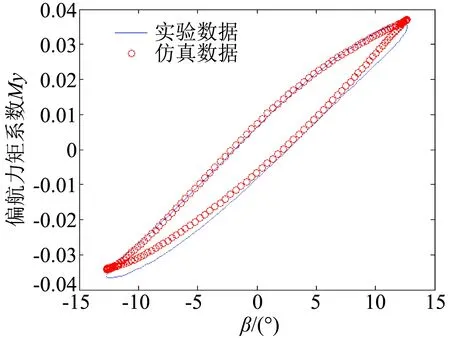
图9 小振幅偏航运动(f=0.4)Fig.9 Small-amplitude yaw motion(f=0.4)

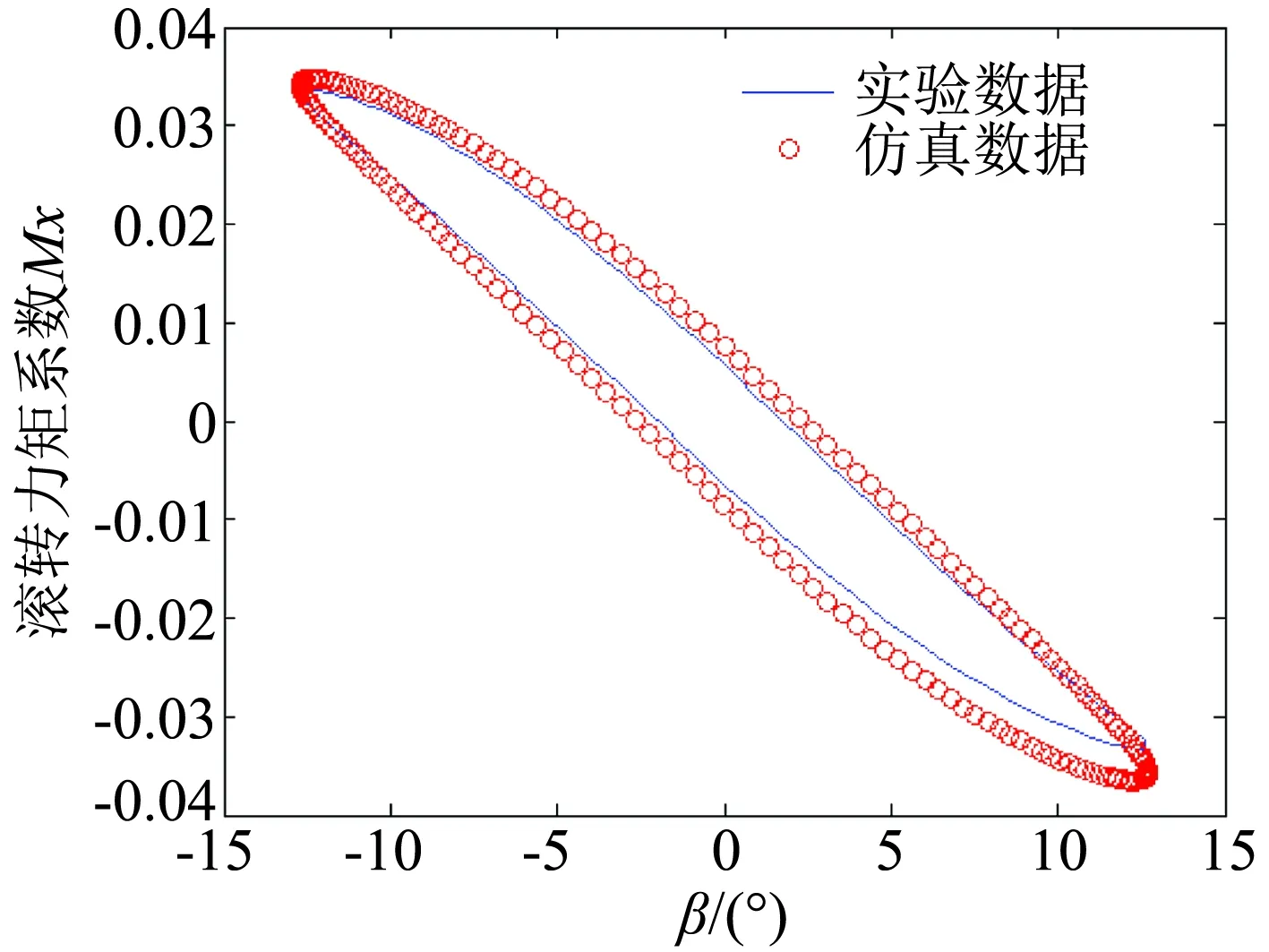
图10 小振幅滚转运动(f=0.8)Fig.10 Small-amplitude roll motion(f=0.8)

3.4 与RTRL算法比较

以单自由度滚转运动为例，对于相同的单自由度滚转运动的实验数据，我们再采用文献[2]中基于RTRL算法的循环神经网络对其滚转力矩系数进行建模，模型训练次数与本文所提EKF-RTRL循环神经网络一样。比较两种算法在相同的训练次数下的拟合程度和误差值。图11是分别采用两种算法时对滚转力矩系数的仿真预测结果与实验结果的比较，图12是两种算法的误差曲线比较。

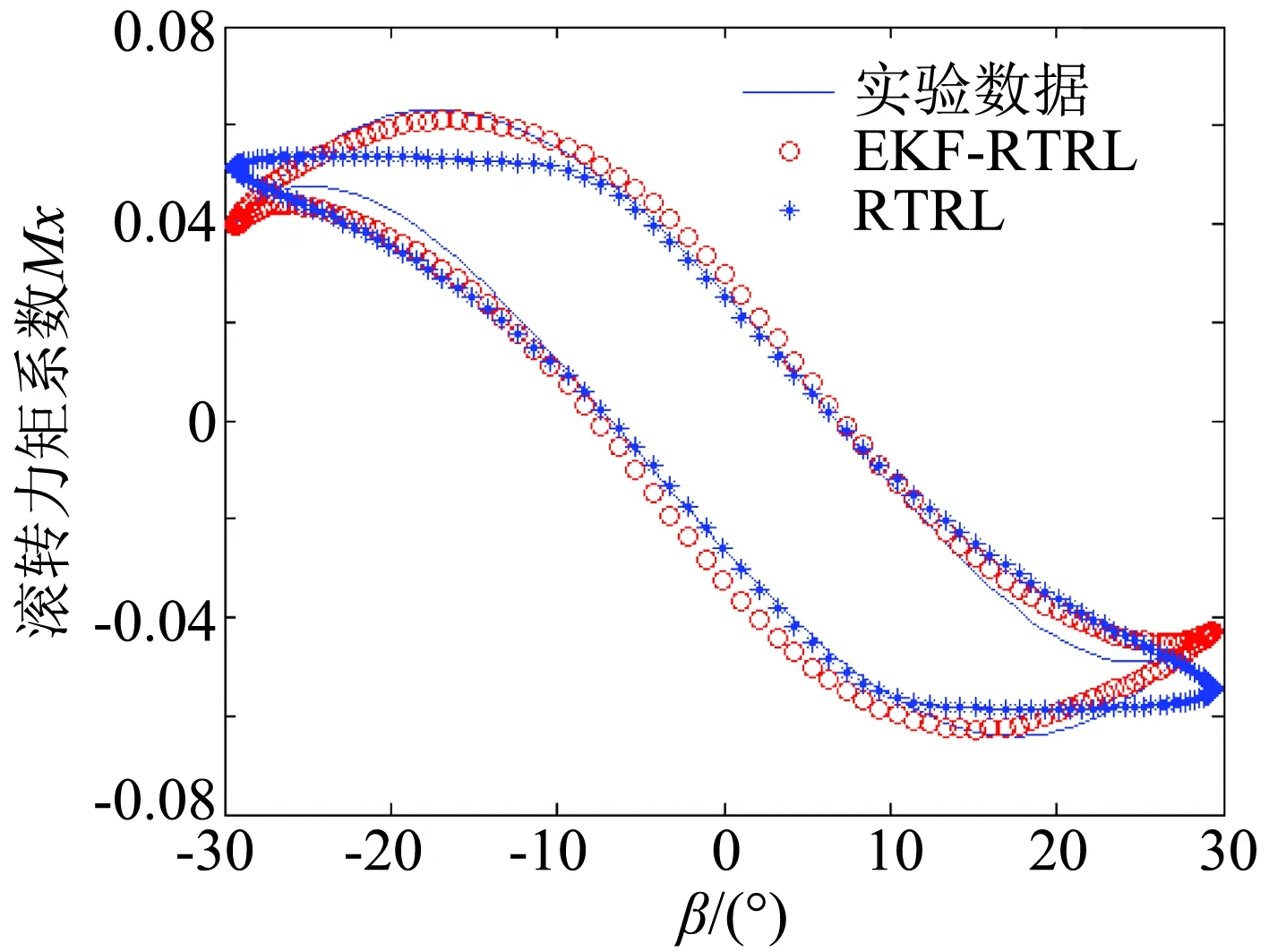
图11 两种算法仿真预测结果与实验结果对比Fig.11 The comparison between the simulation results of two algorithms and the testing results

图12 两种算法的误差曲线对比Fig.12 The error curves of two algorithms

由图11可以看出，EKF-RTRL算法比RTRL算法的拟合程度更高，同时由图12的误差曲线可以看出，EKF-RTRL算法相对于RTRL算法，具有更快的收敛速度和更高的收敛精度，说明本文所提EKF-RTRL的循环神经网络模型在非定常气动力建模上的有效性。

4 结 论

本文讨论了循环神经网络在非定常气动力建模中的应用，结合扩展卡尔曼滤波与实时递归学习算法提出一种EKF-RTRL算法。利用飞机大迎角大振幅单自由度滚转、偏航以及两自由度滚转偏航耦合运动实验数据验证了该循环神经网络模型在对一些非定常气动力建模上的可行性。运用大振幅运动数据建立的神经网络模型在对小振幅运动进行仿真验证时，也同样具有较好的结果，表明该循环神经网络具有一定的适用性。而通过与RTRL算法的对比，说明其既具有RTRL算法收敛精度高的特点，又具备EKF收敛速度快的优点，可以很好的应用在飞机复杂机动的非定常气动力建模上。