超声速飞行器FADS系统实时解算设计与验证

陈广强, 刘吴月, 豆修鑫, 周伟江, 杨云军, 豆国辉

(中国航天空气动力技术研究院 空气动力理论与应用研究所, 北京 100074)

0 引 言

嵌入式大气数据传感(Flush Air Data Sensing, FADS)系统，依靠设计压力传感器阵列测量获取飞行器头部或其它局部位置表面的压力分布，通过特定求解算法模型对压力数据进行转换，间接测量获取飞行过程中的静压、马赫数、迎角和侧滑角等来流参数。FADS系统是超声速飞行器获取飞行大气参数作为飞行控制输入的主要途径，特别是对于吸气式的超声速飞行器尤为重要。对于吸气式超声速飞行器的心脏—亚燃冲压发动机的总体设计，飞行来流的动压和迎角是其中两个重要设计参数，能决定亚燃冲压发动机整个进气道设计的成败。因此精确获得飞行过程中实时来流参数对于飞行器发动机控制及飞行后气动力数据辨识分析是非常重要的。由于来流迎角对亚燃冲压发动机性能影响非常敏感,为了确保亚燃冲压发动机的最佳飞行性能必须精确实时测量飞行来流迎角。通常惯性导航系统安装在弹体内部并受到性能的限制，因此根本不能反映飞行来流大气的变化以及各海拔风速的干扰，也就无法获得真实来流条件下的迎角。FADS系统完全可以满足超声速飞行器亚燃冲压发动机性能设计的需求，并且还具有测量精度高、研制成本低和设备维护相对简单等诸多特点，因此采用FADS测量超声速飞行器的飞行来流迎角等大气参数作为控制系统输入，对于降低飞行器制造的成本和提高总体性能具有重要意义。

FADS技术研究起源于美国航空航天局X-15高超声速飞行器技术验证机项目，现已成功应用到航空航天领域的各个型号，包括航天飞机，战斗机F/A-18/F-22/F-35和“好奇号”火星探测器，以及航空航天局的X系列验证机，如X-31、X-33、X-34、X-38、X-43A等飞行试验项目均开展了FADS技术研究[1-5]。国内关于FADS技术也开展了探索性研究。南京航空航天大学陆宇平教授课题组针对算法、校准，系统误差、标定、FADS与INS组合、故障检测等方面开展了FADS理论的系列研究[6-10]。中国空气动力研究与发展中心李其畅分析了嵌入式大气数据三点解算方法的可行性[11]。西北工业大学李清东探讨了FADS快速智能故障检测和诊断技术[12]。中国航天空气动力技术研究院在FADS理论、风洞验证和飞行试验测试等方面开展了工程应用初步研究[13-15]。

实时数据采集、解算是FADS系统的重要性能。为了进一步研究FADS系统，本文设计了基于BP神经网络的求解算法和基于FPGA+DSP构架数字信号处理解算机的FADS实时解算方案，并在超声速风洞完成实时解算的试验验证。

1 实时解算方案设计

超声速飞行器嵌入式大气数据传感系统算法实时解算方案流程见图1所示，由基于BP神经网络技术的FADS求解算法和解算机组成。图1中虚线方框中为解算机模块。

图1 实时解算方案流程Fig.1 Real-time solving program

解算机采用FPGA+DSP(Field-Programmable Gate Array：现场可编程门阵列，Digital Signal Processor：数字信号处理器)构架设计，由FPGA采集压力数据，送入DSP进行FADS算法实时解算获得来流参数。再将解算结果发送回到FPGA，最后通过FPGA与飞行控制系统通信传输FADS解算结果和接收飞行控制系统的指令。基于FPGA+DSP的实时解算处理系统，充分结合了FPGA和DSP各自的优势和特点。FPGA适合数据量大，对处理速度要求高，但运算结构相对比较简单的底层信号预处理，并且能兼顾速度和灵活性；DSP适合用于运算速度高、控制结构复杂的高层信号算法处理，并且寻址方式灵活和通信机制强大。因此使用FPGA+DSP结构来实现FADS系统算法实时解算设计的最大特点是结构灵活，有较强的通用性，适合模块化设计，从而能提高算法效率；同时其开发周期较短，系统易于维护和扩展。

1.1 基于BP神经网络FADS求解算法

BP神经网络(back propagation)是一种采用误差反向传递算法的神经网络技术。它的基本理论思想是：对于任意给定的自变量x>0和二阶连续函数f(x):[0,1]n→Sn，则一定存在一个三层结构的网络，其能在任意x平方误差精度条件下逼近f(x),由此来看BP网络可以任意逼近一个二阶连续非线性函数，即网络具有二阶精度的性能特点[16-17]。基于BP神经网络的FADS算法正是利用其理论特点建立起来的算法。网络通常设计成三层结构，包括输入层、隐层以及输出层；采用多输入单输出的模式，将各个飞行来流大气参数分别应用神经网络来单独拟合。FADS求解算法的输入为测压孔阵列压力值，输出为对应时刻飞行来流的静压P∞、马赫数Ma、迎角α和侧滑角β。采用Levenberg-Marquardt(LM)方法作为FADS求解算法模型的训练方法，它是目前梯度下降法里综合性能最优的二阶训练方法。

飞行器头部测点阵列压力值是通过采用自主研发CACFD大型计算流体力学数值模拟软件平台求解Navier-Stokes(N-S)方程计算获得。按照已设计弹道飞行包线确定参数测量范围，见表1所示。在测量范围内随机生成4000个样本点。通过对流场数据提取和整理测点阵列压力值，建立样本点来流状态与测点阵列压力值数据表并进行训练获得模型，即可建立基于BP神经网络技术的FADS求解模型。

表1 测量范围Table 1 Measuring range

1.2 数值模拟方法

超声速飞行器头部计算流场为三维单区结构网格，见图2所示。超声速飞行器头部模型(以下简称模型)和测压点几何位置见图3所示。在顶点布置1个测压点，距离头部300mm截面位置和500mm截面位置分别布置4个测压点，总共9个测压点，作为FADS系统测量模型表面压力的阵列。

CACFD软件采用有限体积法对流场进行三维稳态可压缩N-S方程求解，其积分形式的方程见式(1)所示。

图2 空间网格Fig.2 Spatial grid

图3 模型表面和测压点Fig.3 Model surface and FADS points

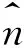
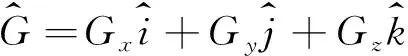
Q为守恒变量，其中包含了密度、动量和总能，表达式为：

Q=(ρρuρvρwρE)T(5)

其中,u、ν和w分别为笛卡尔坐标系下3 个方向的速度，E和ρ分别为总能和密度，总能是内能e和动能的和：

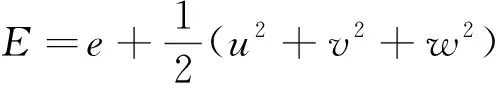
从图4中可以得出，在截面位置X<100 mm，模型表面的压力梯度最大，按照FADS布置原则压力梯度越大的测压点位置，对求解算法的误差精度提高

图4 模型子午线无量纲的压力对比Fig.4 Comparison of dimensionless pressure of meridians

越有利。但是从模型的几何来看，截面位置X<100 mm空间太狭小，无法布置同时布置4个测压点，不得不将第1排测压点放在截面X=300 mm空间更大的位置。为了兼顾模型器内其它设备的安装，将第2排测压点位置在X=500 mm。

1.3 算法设计结果与分析

经过训练后，静压、马赫数、迎角和侧滑角的神经网格均方差分别为4467(均方根误差约为67 Pa)、6.6×10-6(均方根误差约为0.0026)、9.25×10-4(均方根误差约为0.0304°)、3.5×10-4(均方根误差约为0.0169°)。

建模结果见图5～8所示，图中纵坐标分别是全部样本的静压、马赫数、迎角和侧滑角的预测(拟合)绝对误差，横坐标是4000个样本的序号。静压的最大误差300 Pa，而且超过98.5%样本点的静压误差≤200 Pa，马赫数误差范围≤0.015，迎角误差范围≤0.115°，侧滑角≤0.065°。各个神经网络的预测最大误差和均方差对比见表2所示，从表2可以得出最大误差与均方根误差的比值在3.84～5.84之间。

高精度的模型是FADS系统设计成功的重要保证，如果测量系统的总误差为0，则模型的预测误差就是FADS系统测量的误差，但是测量系统总是存在一定的误差。

图5 全部训练样本静压的预测误差Fig.5 Prediction error of static pressure of all training samples

图6 全部训练样本马赫数的预测误差Fig.6 Prediction error of Mach number of all training samples

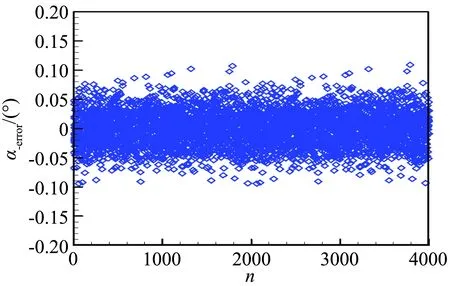
图7 全部训练样本迎角的预测误差Fig.7 Prediction error of angle of attack of all training samples

图8 全部训练样本侧滑角的预测误差Fig.8 Prediction error of angle of sideslip of all training samples

表2 神经网络的训练结果Table 2 Training results of neural networks

1.4 测量总误差影响分析

FADS系统设计的测量精度目标为：自由来流静压测量绝对误差≤500 Pa；飞行马赫数测量绝对误差≤0.1；飞行迎角和侧滑角测量绝对误差≤1°。为了达到该目标，必须要求算法预测能力与测量系统的测量误差能够匹配，即在测量系统设计的误差范围内，算法的预测误差能达到FADS系统设计目标的要求。测量系统的总误差包括传感器误差，管路延迟误差、测压点几何位置误差和解算机模块截断误差等。各个误差带有许多非确定性的参数和随机性，任何一个误差都不能从其它误差中分离出来取单独研究，因此测量总误差的影响研究，目前比较好的方法是蒙特卡洛法，该方法的步骤如下。

第1步：假定测压点总误差均为正态分布，期望为0，方差为σ2。取P1的总误差3σ=200～1000 Pa，取P2～P9的总误差3σ=100～500 Pa。每个测压点分别按照上述正态分布随机生成1000个(理论上该值越大越好，但是考虑计算量不能取过大)随机数。

第2步：将随机误差加到每个测试样本中的压力值，与CFD计算结果比较，求出测量误差方差为σ2时，P∞，Ma，α和β预测误差的平均标准方差，对于静压，计算公式如式7所示。测试样本为本次风洞试验的状态：Ma=2.5～4.0，迎角0°～12°，侧滑角0°～5°(风洞试验为负侧滑角)。

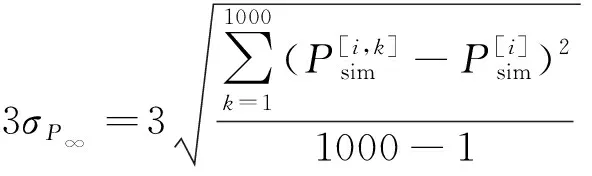
第3步：经过多轮计算结果对比，得出当P1的总误差3σ=900 Pa，P2～P9的总误差3σ=300 Pa时，算法预测误差能达到FADS系统设计目标的要求。见图9～12所示，横坐标均为测试样本的点序号。从图9可以得出，左侧的纵坐标为来流静压(风洞马赫数对应的静压)，从图中可以得出，测压样本的静压(P∞_origin)和FADS算法预测的静压(P∞_sim)基本重合，误差非常小。右侧坐标为3σP∞计算结果，3σP∞≤250 Pa。由图10～12分别得出：3σMa≤0.1，3σα≤0.5°和3σβ≤0.5°。从计算结果可以得出， 当P1～P9的测量系统的总误差3σP1=900 Pa、3σP2～P9=300 Pa时3σMa已经达到设计边界(≤0.1)，而静压3σP∞、迎角3σα和侧滑角3σβ还未达到设计边界，还有一定的误差空间。

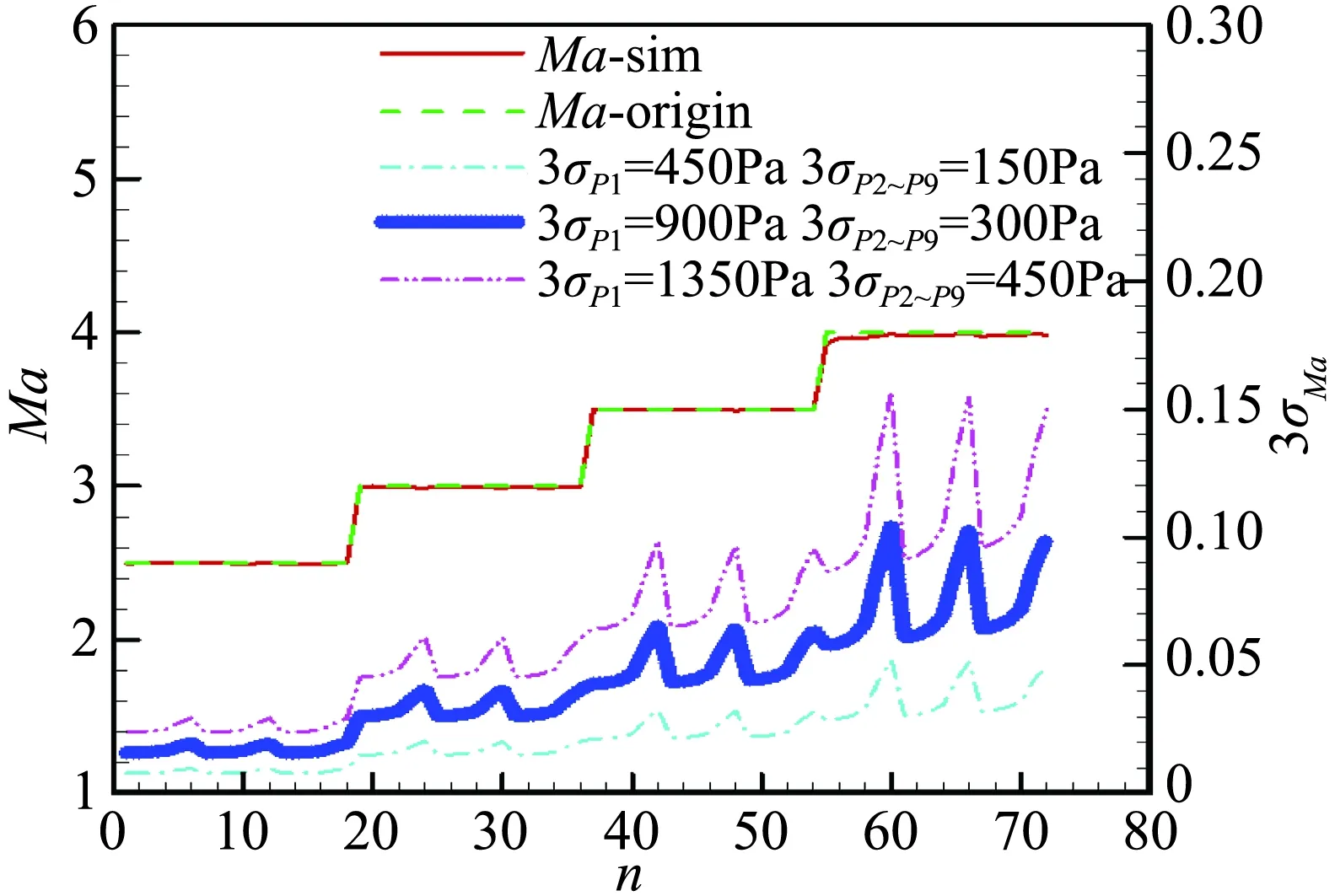
图10 随机测量误差对马赫数的影响Fig.10 The influence of random measurement error on Mach number

图11 随机测量误差对迎角的影响Fig.11 The influence of random measurement error on angle of attack

图12 随机测量误差对侧滑角的影响Fig.12 The influence of random measurement error on angle of sideslip

从图9～图12中，可以得出P1～P9的测量系统的总误差3σP1=450Pa、3σP2～P9=150Pa时，FADS系统设计的测量精度目标还可以进一步提高，但是这对测量系统的总误差提出更高的要求。还可以得出当P1～P9的测量系统的总误差3σP1=1350 Pa、3σP2～P9=450 Pa，FADS系统的测量误差除了3σMa≤0.15超出了设计边界，其它变量还在设计目标范围内，因此本文设计的FADS算法具有较强的抗误差能力。

1.5 解算机设计

解算机由FPGA可编程阵列芯片，DSP芯片，电源模块、通信接口模块以及光耦隔离芯片组成实现。通过FPGA实时采集9路压力数据入DSP，在DSP中按照FADS求解算法模型对采集的数据进行解算，处理结果送回FPGA后再通过RS422串行口输出。电路组成框如图13所示。

设计采用DSP67系列芯片，系统时钟为300 MHz，计算数据采用32位浮点型。DSP中FADS求解算法的计算步骤如下：

图13 电路组框图Fig.13 Circuit block diagram

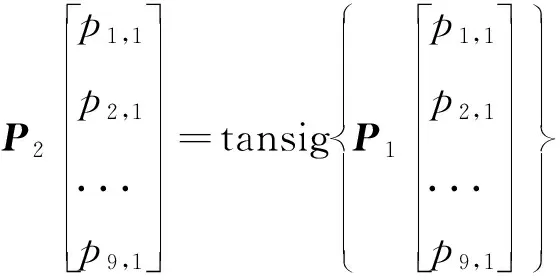
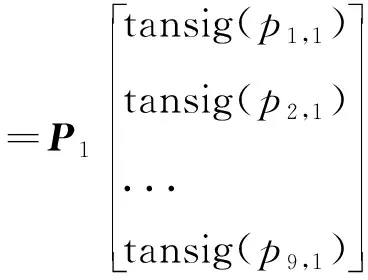
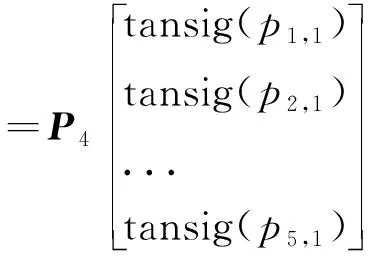
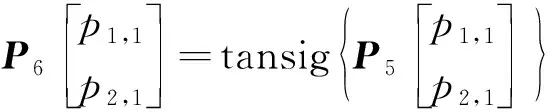
其中：P0为FPGA采集的9路的压力数据；IW1～IW4、B1～B3和B4为神经网络训练获得的矩阵和系数。P7为最终输出，即FADS算法解算获得的来流参数。矩阵和系数共有4组分别用于求解静压、马赫数、迎角和侧滑角，即进行1次FADS解算，需要DSP进行式(7)～式(13)的矩阵运算运行4次。

DSP完成1次式(7)～式(13)矩阵运算需要49989个时钟周期，系统时钟为300MHz。耗时为49989/(300×106)≈0.166 ms，分别获得静压、马赫数、迎角和侧滑角需要运行4次，则FADS算法在解算机上运算1需要时间0.166×4≈0.667 ms。从测试结果来看算法实时解算需要时间小于1 ms，耗时远远低于一般飞行控制系统设计要求10 ms的解算周期。

2 风洞试验结果与分析

2.1 试验介绍

风洞试验是在中国航天空气动力技术研究院FD-12风洞完成。试验模型见图14所示，在风洞中完成马赫数2.5、3.0、3.5、4.0的吹风试验。迎角范围-2～ 12°，迎角12°的试验数据仅作研究参考，检验求解算法模型的外插预测能力，不参加本次试验考核。试验详细状态见表3所示。

图14 试验模型安装在风洞中Fig.14 Test model installed in the wind tunnel

表3 试验状态Table 3 Test status

2.2 试验结果与分析

下面介绍风洞试验中FADS系统的实时测量结果，并与风洞系统的测量结果进行比较。由于试验数据较多，且Ma=3.5数据与Ma=4.0数据误差结果相近，因此只介绍Ma=2.5、3和4具有代表性的部分数据。各图中横坐标均为采样时间历程，单位为0.01 s(采样频率100 Hz)。风洞系统只测量总压、马赫数和迎角，马赫数是风洞系统测量给出的是一个平均值，总压和迎角都是与FADS同步进行实时测量。迎角是由风洞迎角机构控制，每个迎角状态持续6 s～8 s，按照采样频率则每个迎角状态采样6000～8000个点(0.01 s)。侧滑角是由已标定的支杆机构直接给出，试验中不作测量。风洞的静压是根据风洞系统测量总压和马赫数换算获得，见公式(14)所示。式中Pt为总压，P∞为静压，γ=1.4，为空气比热比。

如图15～18所示为Ma=2.5，β=-3°试验状态，FADS测量结果与风洞测量结果的对比。从图15中可以得随着迎角变化，压力出现微小振荡，FADS解算结果与风洞系统测量结果最大误差约970 Pa，最小误差约为380 Pa。由图16得出马赫数与试验马赫数误差较小，绝对误差<0.1。图17和18得出FADS测量迎角与风洞系统迎角机构的迎角误差<1°，侧滑角误差<0.5°。

图15 Ma=2.5 ,β=-3° FADS测量与风洞测量静压对比Fig.15 Comparison in static pressure measurement results between FADS and wind tunnel at Ma=2.5, β=-3°

图16 Ma=2.5, β=-3° FADS测量与风洞测量马赫数对比Fig.16 Comparison in Mach number measurement results between FADS and wind tunnel at Ma=2.5, β=-3°

图17 Ma=2.5, β=-3° FADS测量与风洞测量迎角对比Fig.17 Comparison in angle of attack measurement results between FADS and wind tunnel at Ma=2.5, β=-3°

图18 Ma=2.5, β=-3° FADS测量与风洞测量侧滑角对比Fig.18 Comparison in angle of sideslip measurement results between FADS and wind tunnel at Ma=2.5, β=-3°

如图19～图22所示为Ma=3，β=-5°试验状态，FADS测量结果与风洞测量结果的对比。从图19得出FADS测量静压与风洞系统测量的静压最大误差<400 Pa，静压测量结果随着迎角变化比图15更加平缓。图20所示为马赫数测量结果对比，绝对误差<0.1。图21和22分别为迎角和侧滑角的测量结果对比，迎角的绝对误差<1°，侧滑角的绝对误差<0.5°。

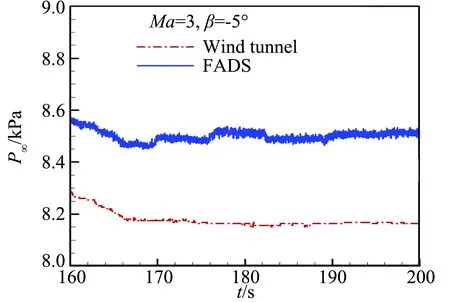
图19 Ma=3 , β=-5° FADS测量与风洞测量静压对比Fig.19 Comparison in static pressure measurement results between FADS and wind tunnel at Ma=3.0, β=-5°

图20 Ma=3, β=-5° FADS测量与风洞测量马赫数对比Fig.20 Comparison in Mach number measurement results between FADS and wind tunnel at Ma=3.0, β=-5°

图21 Ma=3, β=-5° FADS测量与风洞测量迎角对比Fig.21 Comparison in angle of attack measurement results between FADS and wind tunnel at Ma=3.0, β=-5°

图22 Ma=3, β=-5° FADS测量与风洞测量侧滑角对比Fig.22 Comparison in angle of sideslip measurement results between FADS and wind tunnel at Ma=3.0, β=-5°

如图23～26所示为Ma=4，β=0°试验状态，FADS测量结果与风洞测量结果的对比。从图23可以得出静压测量最大误差<300 Pa，在小迎角-2°～6°时两条曲线基本重合，在10°～12°时误差增大。图24得出马赫数在迎角-2°～10°时最大误差<0.1，迎角12°时，误差最大为0.12。图25和26得出，迎角的绝对误差<1°，侧滑角误差<0.5°。

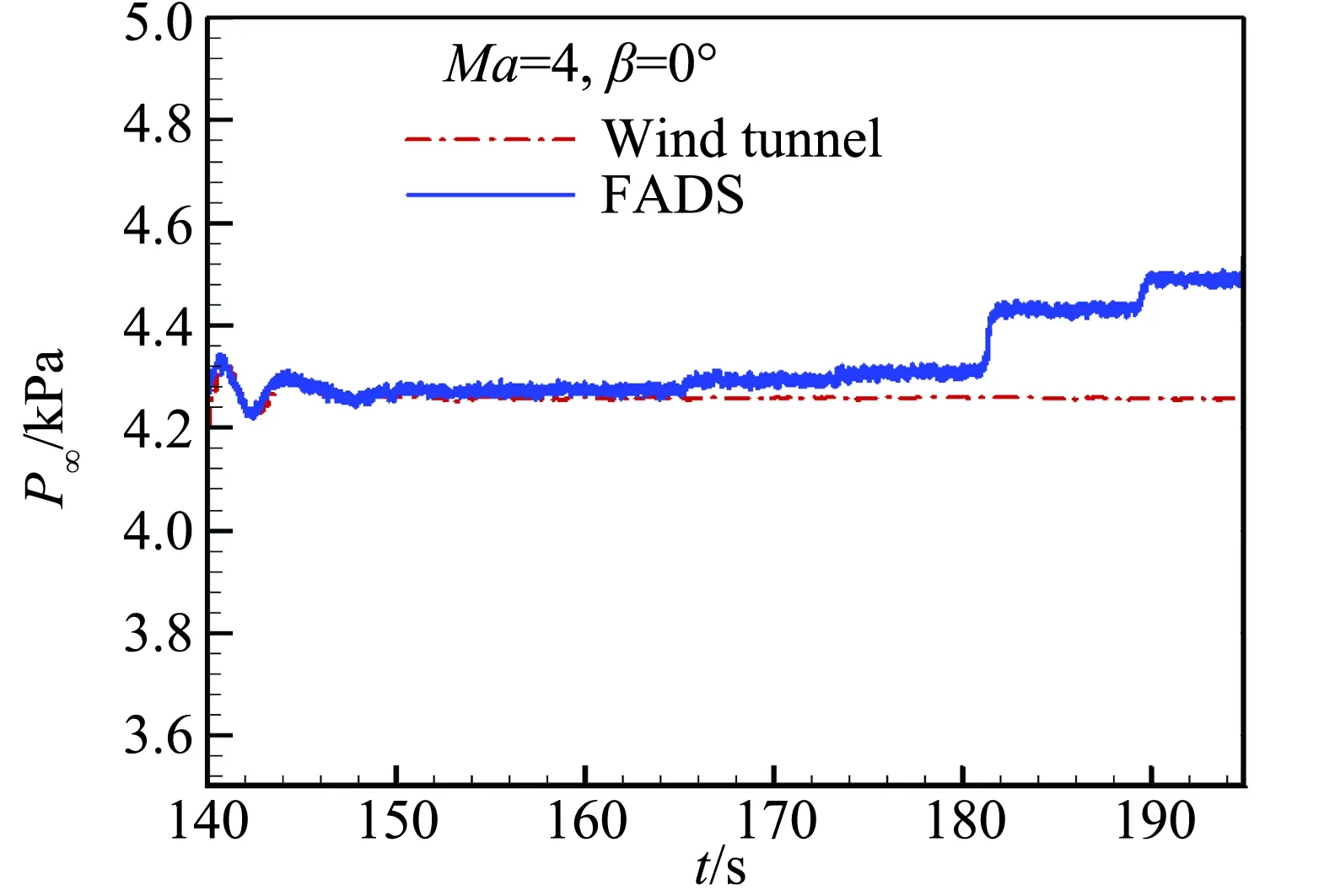
图23 Ma=4 , β=0°FADS测量与风洞测量静压对比Fig.23 Comparison in static pressure measurement results between FADS and wind tunnel at Ma=4.0, β=0°

图24 Ma=4, β=0°FADS测量与风洞测量马赫数对比Fig.24 Comparison in Mach number measurement results between FADS and wind tunnel at Ma=4.0, β=0°

图25 Ma=4, β=0°FADS测量与风洞测量迎角对比Fig.25 Comparison in angle of attack measurement results between FADS and wind tunnel at Ma=4.0, β=0°

表4所示为风洞试验马赫数2.5～4.0共4个马赫数试验结果误差的统计表。从表中可以得出静压最大误差970 Pa，随着马赫数增加，静压的绝对误差减小，静压相对误差先减小后增大，这是由于静压绝对值减小而造成的。在迎角-2°～10°，Ma=2.5～4.0马赫数误差均<0.1。迎角和侧滑角的误差均<1°，并且大部分试验状态侧滑误差<0.5°。Ma=4.0，迎角12°马赫数误差达到最大为0.12，试验结果表明求解算法模型还具有一定的外插预测能力。

图26 Ma=4, β=0°FADS测量与风洞测量侧滑角对比Fig.26 Comparison in angle of sideslip measurement results between FADS and wind tunnel at Ma=4.0, β=0°

表4 试验结果误差统计表Table 4 Statistics of test result errors

2.3 误差分析及试验改进

从试验结果得出，静压绝对误差随着马赫数增加而减小，相对误差则先减小后增大。静压绝对误差受到风洞不同马赫数段的影响非常明显。因此可以对Ma=4的风洞流场进行标定，寻找流场品质最佳位置进行试验才能获得最准确的静压测量误差。

在Ma=2.5，马赫数误差在(-0.05，0.05)内，误差非常小，在Ma=3.0时，马赫数误差在小迎角时(-2°～6°)非常小，但是到了大迎角时(10°～12°)误差增加(>0.05)。在Ma=4.0时，马赫数的误差变化趋势，与Ma=3.0的近似，小迎角时误差小，大迎角时误差增加(>0.1)。由于P1点对FADS算法解算马赫数起到绝对的作用，对比Ma=2.5、3、4.0的P1点压力，见图27～29所示。

从图27～29可以得出，试验测量的P1压力值均比CFD计算压力值要偏大，迎角-2°～6°时，试验测量的压力与CFD计算压力趋势吻合较好，只是存在等距偏差，在迎角10°～12°，P1压力值的偏差增大。从图中所示最大相对误差可以得出，随着马赫数的增加，最大相对误差由3.89%增大到6.29%。由于FADS求解模型是基于CFD数据建立的，所以这是造成大迎角FADS测量马赫数误差增大的主要原因。因此可以通过修正训练样本中CFD计算P1的压力值或是改进计算网格和数值方法降低CFD计算P1的误差，重新训练神经网络建立FADS求解算法模型，这样可以提高FADS系统在大迎角的测量精度。

图27 Ma=2.5，β=0°的P1点压力对比Fig.27 Comparison in P1 pressure between CFD and wind tunnel at Ma=2.5, β=0°

图28 Ma=3.0，β=0°的P1点压力对比Fig.28 Comparison in P1 pressure between CFD and wind tunnel at Ma=3.0, β=0°

图29 Ma=4.0，β=0°的P1点压力对比Fig.29 Comparison in P1 pressure between CFD and wind tunnel at Ma=4.0, β=0°

如图30所示为Ma=4，β=0°试验状态，将模型翻转180°的FADS测量迎角和风洞系统测量迎角结果对比。从图中可以得出迎角的误差小于0.5°，比前面几个状态吻合都更好。本次试验结果表明风洞模型的安装存在一定的同轴度的误差。因此在开展试验前，一定要对支杆和模型装配进行标定，或者在设计试验模型的装配时尽量考虑对同轴度的影响。

图30 Ma=4, β=0°FADS测量与风洞测量迎角对比Fig.30 Comparison in angle of attack measurement results between FADS and wind tunnel at Ma=4.0, β=0°

3 结 论

研究得出以下结论：

1) 在试验过程中FADS算法实时解算未出现解算故障或跳点，能灵敏反映出来流参数的变化、具有很好的鲁棒性和敏捷性。验证了基于BP神经网络技术的求解算法和基于FPGA+DSP构架数字信号处理的解算机的算法实时解算方案的可行性。

2) FADS系统测量结果与风洞系统测量结果吻合良好。Ma=3.0，3.5，4.0全部变量的测量误差均达到了设计指标； 受到风洞流场影响，Ma=2.5静压测量误差达不到设计指标，其它变量则均达到设计指标。验证了FADS算法设计的测量精度。

3) 通过误差分析发现了不同风洞马赫数对静压测量误差存在明显影响，在大迎角时FADS系统测量马赫数的误差增大，以及模型存在同轴度误差等问题。对问题进行分析，提出试验改进方法。