基础实验题B:线性及非线性LC振荡电路

王思慧,范文凯,江洪建,万建国

(南京大学 a.物理学院；b.匡亚明学院，江苏 南京 210093)

第4届全国大学生物理实验竞赛基础性实验试题B为“线性及非线性LC振荡电路”. 试题第1部分涉及线性电路的暂态及稳态性质，包括LR，RC及RLC电路，是大学物理及大学物理实验的常规内容[1-3]. 这一部分考察基础知识和实验能力. 试题第2部分涉及非线性电路，在线性LC振荡电路基础上，增加了非线性阻尼器件，要求学生参照线性振荡电路的性质，初步了解非线性振动的性质. 例如,稳态响应中幅频特性的共振频率受到驱动电压的影响而变化；响应信号不仅存在与驱动信号相同的基频，也存在倍频分量等. 这一部分旨在考察学生通过实验观察理解概念，探索物理规律的能力.

1 实验内容

1.1 实验器材

数字示波器，信号发生器(示波器和信号发生器提供简要使用说明)，黑盒子(内含1个电感L，1个电容C，1个非线性器件X)，电阻箱1只，导线若干，坐标纸若干张. 黑盒子示意图见图1.

图1 黑盒子示意图

1.2 RLC振荡电路(电路A)的暂态和稳态过程研究(实验1)

RC电路、RL电路及RLC电路在物理研究和工程技术方面有广泛的应用，例如微分电路、积分电路、相移电路和振荡电路等. 实验中的RLC谐振电路可以用于观察线性振动系统的波形、相图，研究振动系统的幅频特性、相频特性等. 此外还考察了利用数字示波器观测电信号的波形，测量频率、幅值以及相位差的方法.

RLC串联电路暂态过程的方程为[3]

(1)

(2)

(3)

(4)

该部分实验需要学生完成以下内容：

1)判断本实验所提供的器件的种类(L或者C以及非线性器件X)，并测量线性器件的参量.

2)RLC暂态过程. 搭建RLC串联电路，画出电路图. 选取适当的信号源输出波形、电压和频率. 用示波器观察阻尼振荡、过阻尼振荡和临界阻尼振荡的uC-t图形，分别记录对应的电阻箱的阻值R0. 设定电阻箱的阻值R0为0及100 Ω，测量在阻尼振荡时电路的总电阻R、振荡周期T、时间常量τ以及品质因数Q值. 用示波器观察并在坐标纸上定性描绘阻尼振荡情况下的“相图”(即电流和电量的近似关系图像).

1.3 非线性LC振荡电路(电路B)的研究(实验2)

将器件X串联接入电路A，形成非线性振荡电路B.

1)研究电路B的暂态以及稳态性质. 参照RLC暂态过程的性质，研究电路B的暂态过程. 用示波器显示该电路中电容电压uC与时间t的关系曲线，并在坐标纸上描绘示波器所显示的图像. 用示波器观察并在坐标纸上定性描绘该电路的“相图”(即电流和电量的近似关系图像). 与电路A的暂态性质相比较，说明电路B有何不同.

2)参照RLC稳态过程的性质，研究电路B的稳态过程. 自拟实验步骤和测量内容，观察电路B的幅频特性(uC-f). 研究共振频率与什么参量有关，并将结果记录在坐标纸上. 在此基础上，说明与电路A的幅频特性有何不同. 利用示波器的Math-FFT功能可以获得响应信号uC的频谱，研究电路的非线性谐振特性，观察并说明频谱有什么特征？研究这些特征与哪些参量有关？

2 参考解答与竞赛结果分析

2.1 RLC振荡电路(电路A)的暂态和稳态过程研究

2.1.1 实验所提供的器件

1，2，3分别为C，L和X(参量略). 器件种类的判断和参量测量涉及LR，RC及RLC电路的暂态或稳态性质[1-3]，可以有多种方法，在此不限制解答方法，只要求得到结果.

混凝土浇捣后，先按设计标高用2 m刮尺刮平，混凝土收水并开始初凝时，用木抹子进行抹压，将面层的小凹坑、气泡眼、砂眼和脚印等压平。在混凝土终凝前再进行二次抹面，用木抹子找平，搓磨2～3次，以提高混凝土的表层密度，消除收缩裂缝及混凝土表面的其他痕迹，形成最终的混凝土面。

2.1.2RLC暂态过程

1)搭建RLC串联电路，如图2所示. 信号源输出用低频方波信号(如方波频率200 Hz,Upp=5 V)，调整电阻箱的阻值，可以观察并记录RRC的过阻尼以及R=RC的临界阻尼振荡图像.

图2 RLC串联电路

3)为了得到阻尼振荡的“相图”，即电流和电量的近似关系图像，理论上可以用电阻上的电压UR(正比于电流)以及电容上电压UC(正比于电量)的图像来描述. 信号依然是低频方波. 实验中由于示波器2个通道以及信号源共地，无法直接获得UR和UC. 将图2中的R与C调换位置，并且使电阻箱阻值设为很小(几Ω，远小于电容器阻抗)，示波器通道1跨接在UR和UC两端，忽略UR之后，近似当作UC的值；通道2测量UR的值，利用示波器的X-Y模式，则可以定性观察相图. 图像略，示意图见文献[4].

2.1.3RLC稳态过程

1)测量幅频特性曲线电路图如图2所示. 信号源输出正弦信号，设定电阻箱的阻值R0，测量增益(uC/uin，uin指输入电压)与信号频率的关系，记录实验数据，并将结果作图，见图3.

2)根据幅频特性曲线结果以及题干的提示，可以求共振频率f0以及品质因数Q.

图3 幅频特性曲线

2.2 非线性LC振荡电路

2.2.1 暂态过程

器件X是1对反向并联的二极管，在电路中作为非线性阻尼器件. 将器件X串联接入电路A，形成非线性振荡电路B， 如图4所示. 信号源输出仍采用低频方波信号. 实验方法参考RLC暂态过程，原理参考文献[4-5].

图4 非线性LC振荡电路

1)使电阻箱阻值设为很小，则示波器通道1显示uC与时间t关系曲线，示意图见图5.

2)根据图4电路，示波器的X-Y模式近似地显示“相图”，示意图见图6.

图5 uC与时间t关系曲线

图6 非线性LC振荡电路的相图

3)与电路A的暂态性质相比较，电路B有以下几点不同：暂态过程起振电压需要达到一定阈值；振荡次数为有限的几次(振幅几乎是线性衰减)；存在欠阻尼到过阻尼的转换，即某一时间点之后信号单调衰减，不再往复振荡；电容器电压存在最终无法衰减到零的情况.

2.2.2 稳态过程

实验方法参考前面RLC稳态过程，实验原理参考文献[5].

1)幅频特性曲线见图7. 与电路A相比较，电路B有以下不同：信号源驱动电压较大时共振峰频率几乎不变，而后随着驱动信号电压减小共振频率先是减小，最后共振峰消失. 而线性共振频率与驱动电压大小无关. 也可以测量共振峰频率与驱动信号电压的关系，见图8. 此外增益也随驱动信号电压减小而减小.

2)非线性谐振：利用示波器的FFT容易观察响应信号uC的频谱(图略). 当信号源输出频率f时，频谱中存在f以及3f，5f等倍频谐振. 可以观察频谱的基频和3倍频振幅对于驱动频率以及振幅的响应. 稳态响应也存在起振阈值，基频振幅对信号源输出电压振幅敏感，倍频振幅则不敏感.

图7 电路B的幅频特性曲线

3 评 论

在判断元器件部分，有17位考生申请了提示卡，均分只有3.79分，15位考生得0分. 这反映了实验基础知识尚有待加强.

在RLC暂态过程部分. 均分6.6分，1人满分，1人0分，得分情况好于第1小题. 这一部分考察阻尼振荡、临界阻尼、过阻尼现象，以及测量时间常量τ、品质因数Q值等内容，要求基础知识掌握较好；阻尼振荡相图的观察在掌握基础知识的基础上，还有进一步的延伸，因此本题在方法上有所提示. 这一部分个别考生得到满分，而多数考生表现平平，反映了基础知识和和应变能力方面的差距.

在RLC稳态过程部分，均分8.39分，2人满分，10人0分. 考察RLC串联谐振电路的幅频特性，从物理概念到实验电路均是学生较熟悉的内容，是基础实验题B得分率最高的小题，也是多数考生的主要得分项.

非线性LC振荡电路是多数考生陌生的内容. 因此实验2对于实验方法做了提示说明，要求参照线性RLC电路的方法进行对比实验，初步了解非线性电路的一些性质. 在有限的考试时间内完成这部分实验要求是相当高的. 这一部分共40分，均分2.63，最高分21分，56人中21人有净得分. 其中暂态过程20分，最高分12分；稳态过程20分，最高分9分.

表1是对56名参赛者实验成绩的统计结果. 图9是按分项和总分的统计结果. 结果显示，实验1试题难度适中，区分度较好，能够反映考生基本知识和实验方法的掌握情况. 实验2注意实验方法和原理的延伸扩展，试题内容的设计上富有启发性，对优秀选手有区分度，并能够充分反映高水平选手的知识迁移能力和应变能力.

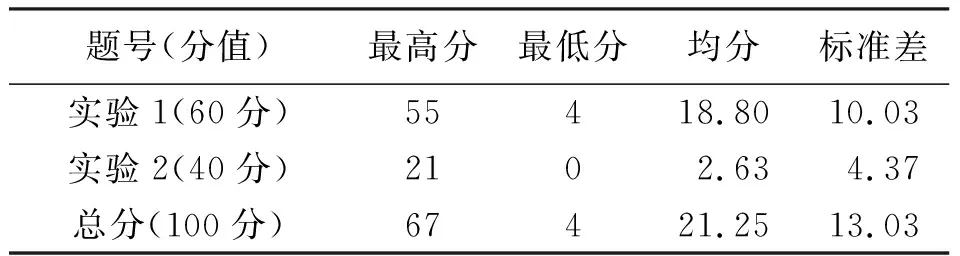
表1 基础实验试题B成绩统计

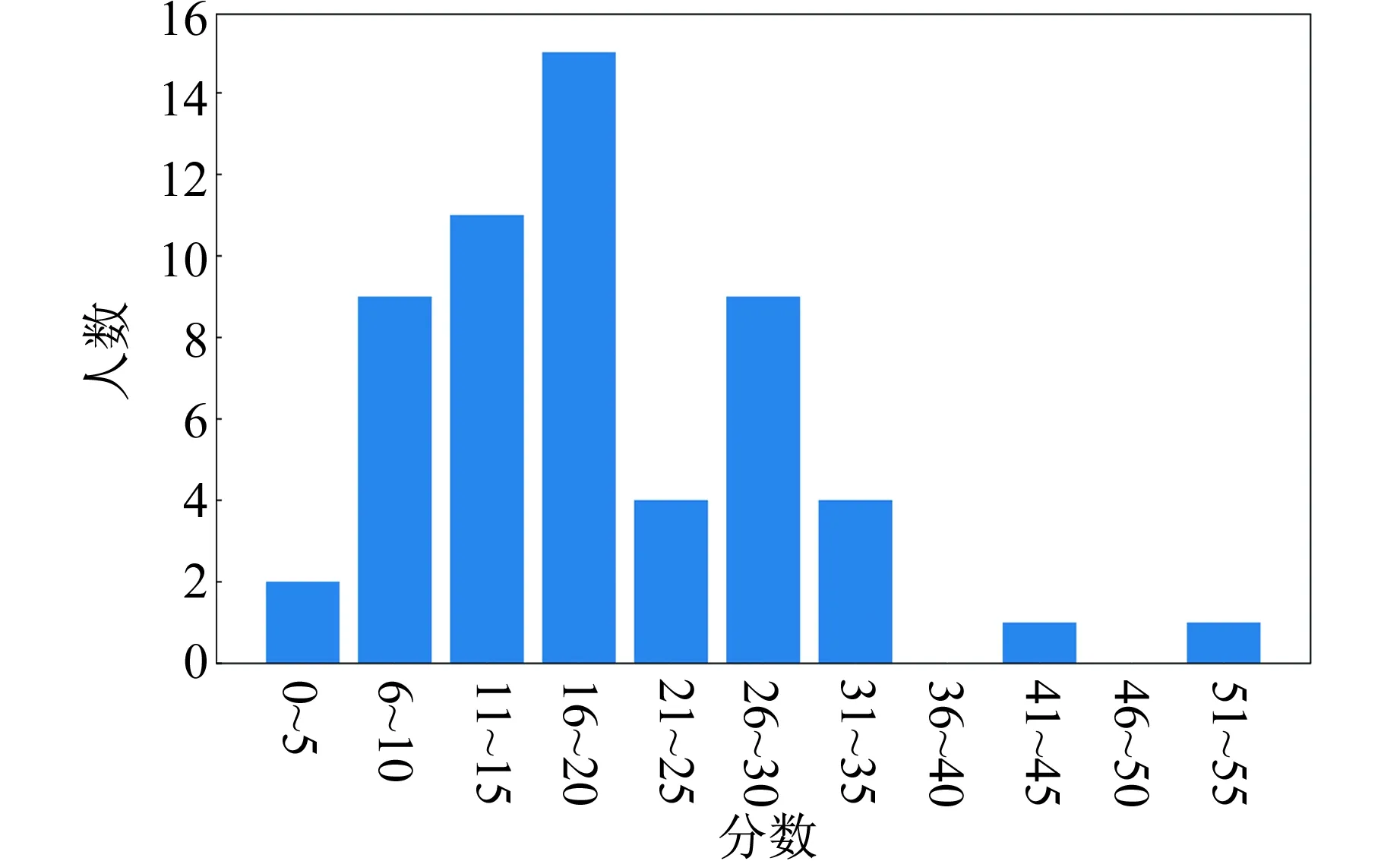
(a)实验1得分

(b)实验2得分

(c)总分图9 实验成绩的统计结果

除了作为考题，本实验还可以作为RLC电路实验的拓展补充，用于演示线性和非线性振动的基本现象和性质. 例如，用数字示波器显示线性振子和非线性振子的动力学过程， 使得理论较为抽象的相图、非线性振动的频谱等方便地得到展示. 实验中所用的非线性电路还可以用来模拟干摩擦阻尼作用下的弹性振动系统，简化了实验装置和测量方法，丰富了实验内容.