线性时滞系统稳定性优化技术研究

方庆霞，王彩卓，何颖子

(贵州工程应用技术学院 理学院，贵州 毕节 551700)

系统的主要变化趋势，不仅受到当前状态的影响，也与过去一段时间的运行状况具有十分紧密的联系.如果从控制理论入手看待系统的运行情况，可知系统当前阶段的状态，是由过去状态衍生而来，且这种衍生关系将会一直保持下去，这种保持时间滞留特性的系统，就被称为时滞系统.时滞现象在各类工程应用系统中都时有发生，最常见的包括神经网络、工业核反应堆及飞机飞行控制器等[1].如何更好地提升系统稳定性、实现控制系统持久稳定地运作，是现阶段时滞系统亟待改进的问题.时滞现象的发生，不仅会在一定程度上降低系统的综合能动性，也会使系统陷入一种波动状态，无法保持高度稳定性，进而给人为控制系统造成较大困扰.传统时滞系统依靠时滞模型，计算系统的基础时延，再通过联立基础时延与系统运行时间的方式，确定系统过去运行状况对当前阶段状态的影响程度[2-3].这种方式需要大量的数据运算，才能保证时滞模型的准确无误，不仅造成大量人力资源的浪费，也不能从根本上提升系统的稳定性.为改善这种不良的系统形态，对线性常时滞系统、线性变时滞系统的稳定性优化技术进行研究，力求早日实现人为控制系统运行的目的.

1 线性常时滞系统稳定性优化技术

线性常时滞系统的稳定性优化技术，由基于积分不等式、基于增广Lyapunov、基于二次凸组合三方面应用的分析组成，具体研究过程，可按如下步骤进行.

1.1 基于积分不等式的稳定性优化

基于积分不等式的线性常时滞系统稳定性优化分析，主要针对积分不等式、时滞相关稳定性两项定理进行[4].积分不等式定义可描述为：在任意符合维数条件的恒定矩阵W中，存在两个标量a和b，若a、b间的关系满足ab，则如公式(1)所示的积分不等式恒成立.

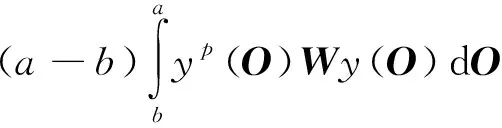
(1)

其中，y代表固定时滞指标，O代表时滞原矩阵，p代表指标固定系数.时滞相关稳定性，对固定时滞指标y的限制条件可表示为：

(1+k)y<0

(2)

其中，k代表时滞相关稳定系数.若某系数同时满足公式(1)和(2)，则可认为该系数即为一个固定时滞指标y.通过这种寻找y的方式，完成基于积分不等式的线性常时滞系统稳定性优化分析.

1.2 基于增广Lyapunov的稳定性优化

基于增广Lyapunov的线性常时滞系统稳定性优化分析，包含Lyapunov泛函定义的提出及证明两部分.Lyapunov泛函定义，对固定时滞指标的缩放范围进行限制，且这种限制关系的确定，一定程度上利用自由权矩阵法，增加保守性估计的准确性[5].Lyapunov泛函定义可具体表示为：

U(y)=U1(y)+U2(y)+L+Un(y)

(3)

其中，U代表Lyapunov泛函定义结果，U1，U2，…，Un代表Lyapunov泛函定义过程的参与量，y代表固定时滞指标，n代表Lyapunov泛函的定义次数.上述过程，完成Lyapunov泛函定义的提出，利用公式(3)的计算结果U(y)，可将Lyapunov泛函定义的证明流程表示为图1.

图1 Lyapunov泛函定义的证明流程图

根据图1可知，当某参数疑似固定时滞指标y时，通过公式(3)，计算出该参数的Lyapunov泛函定义结果U(y)，再利用公式(1)和(2)，对该参数的固定时滞限制条件进行计算.若计算结果真实有效，则认为由该参数完成的Lyapunov泛函定义成立，否则认为该参数不满足固定时滞指标y的选取条件.通过上述过程，完成基于增广Lyapunov的线性常时滞系统稳定性优化分析.

1.3 基于二次凸组合的稳定性优化

基于二次凸组合的线性常时滞系统稳定性优化分析，可以利用公式(3)的计算结果，对固定时滞指标y的保守稳定性规则进行深度规划[6].规定x1，x2，x3，x4分别作为固定时滞指标y的四个方向向量，其中每个向量与固定时滞指标y间的关系，可表示为：

(4)

如果这四个方向向量间的关系满足x1≠x2≠x3≠x4≠0，则下面的式子成立：

(5)

其中，f(x1)，f(x1)，f(x3)，f(x4)分别代表固定时滞指标y四个方向向量的简单规划结果，r代表凸组合系数，ξ代表稳定性优化常数.联立公式(3)、(4)、(5)，可完成基于二次凸组合线性常时滞系统的稳定性优化分析.

2 线性变时滞系统稳定性优化技术

线性变时滞系统的稳定性优化技术，由一般型、中立型、混合型三方面应用的分析组成，具体研究过程，可按如下步骤进行.

2.1 一般型变时滞系统的稳定性优化

一般型变时滞系统的稳定性优化分析，主要针对非固定时滞指标进行.非固定时滞指标被定义为一种非正规标量，在具有镜面对称关系的对角矩阵中，这种非正规标量可以随着矩阵维数的变化而变化[7].假设具有镜面对称关系的对角矩阵，共包含8个不全等行关系、8个不全等列关系.其中第一行8个元素，可用数字1～8代替；第二行第一个元素为非固定时滞指标，其余7个元素，可用数字1～7代替；第三行前两个元素为非固定时滞指标，中间四个元素，可用数字1～4代替，其余两个元素为0；第四行前三个元素为非固定时滞指标，其余5个元素，可用数字1～5代替；第五行前四个元素为非固定时滞指标，其余4个元素，可用数字1～4代替；第六行前五个元素为非固定时滞指标，中间2个元素，可用数字1～2代替，最后一个元素为0；第七行前六个元素为非固定时滞指标，第7个元素为数字1，最后一个元素为0；第八行前七个元素为非固定时滞指标，最后一个元素为数字1.这种具有镜面对称关系的对角矩阵结果，可表示为图2.

图2 一般型变时滞系统的对角矩阵结构图

在图2所示的对角矩阵中，α代表非固定时滞指标，通过分析该指标，在矩阵中所处的具体位置及所占比重，可完成一般型变时滞系统的稳定性优化分析.

2.2 中立型变时滞系统的稳定性优化

中立型变时滞系统的稳定性优化分析，是在图2所示对角矩阵的基础上，研究当镜面对称关系不存在时，系统时滞现象的变化情况[8].为了更方便地表现出中立型时滞系统稳定性的变化情况，将规范的8行8列矩阵，拆分成4个4行4列矩阵.每一个矩阵的第一行4个元素，都可以用数字1～4代替；第二行第一个元素为非固定时滞指标，其余3个元素，可用数字1～3代替；第三行前两个元素为非固定时滞指标，第三个元素可用数字1代替，最后一个元素为0；第四行前三个元素为非固定时滞指标，最后一个元素可用数字1代替.按照左上、右上、左下、右下的顺序，可将这4个矩阵依次编号为1，2，3，4，具体矩阵结构及相互之间的对应关系，如图3所示.

图3 中立型变时滞系统的分矩阵结构图

图3中带有箭头的直线，代表分矩阵中非固定时滞指标α的流动关系.分析图3可知，分矩阵(1)中非固定时滞指标α，可自发地流向分矩阵(2)和分矩阵(3)；分矩阵(2)中的非固定时滞指标α，可自发地流向分矩阵(3)和分矩阵(4)；分矩阵(3)中非固定时滞指标α，可自发地流向分矩阵(4).分析非固定时滞指标α在每个分矩阵中所占比重，并记录α的每一次流动时间，利用上述两组数据，完成中立型变时滞系统的稳定性优化分析.

2.3 混合型变时滞系统的稳定性优化

混合型变时滞系统的稳定性优化分析，是在图2所示对角矩阵的基础上，研究当镜面对称关系部分存在时，系统时滞现象的变化情况[9-10].为了更方便地表现出混合型时滞系统稳定性的变化情况，将规范的8行8列矩阵，拆分成2个4行8列矩阵.每一个矩阵的第一行8个元素，可用数字1～8代替；第二行第一个元素为非固定时滞指标，中间6个元素，可用数字1～6代替，最后一个元素为0；第三行前两个元素为非固定时滞指标，中间4个元素，可用数字1～4代替，最后两个元素为0；第四行前三个元素为非固定时滞指标，中间2个元素，可用数字1和2代替，最后三个元素为0.按照由上至下的顺序，可将这2个矩阵编号为1和2，具体矩阵结构及相互之间的对应关系，如图4所示.

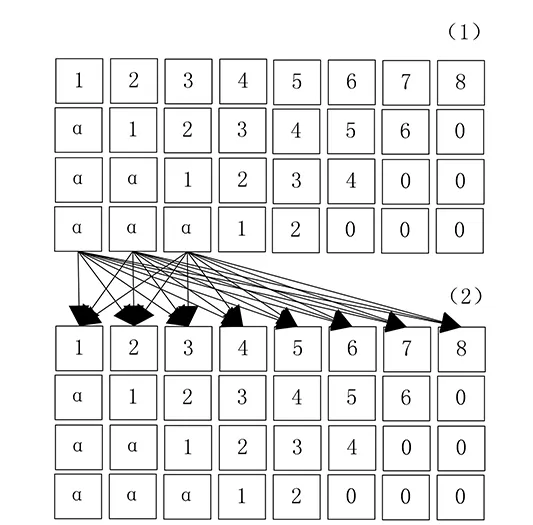
图4 混合型变时滞系统的分矩阵结构图

分析图4可知，分矩阵(1)最后一行包含3个非固定时滞指标α，分别处于该行的第1、2、3列.这三个非固定时滞指标α，可自发地流向分矩阵(2)第一行中的每一个元素，形成一种非固定时滞指标与数字相连的形式，且这种形式不可逆.而分矩阵(1)中第2行、第3行的非固定时滞指标α，不可以进行自发流动.分矩阵(2)中，所有非固定时滞指标α，都不可以进行自发流动，处于该矩阵的所有元素，只具有承受能力，不具有发送能力.分别记录分矩阵(1)中，最后一行3个非固定时滞指标α，流向分矩阵(2)中第一行元素的时间，并计算分矩阵(1)和(2)中所有非固定时滞指标α占总元素的比重，利用上述两个计算结果，完成混合型变时滞系统的稳定性优化分析.

3 实验结果与分析

上述过程，完成新型时滞系统稳定性优化技术研究.为验证优化后时滞系统的实用性价值，设计如下对比实验.以两台配置完全一样的计算机，作为实验对象，随机挑选一台计算机，并在其中安装优化后时滞系统应用程序，将其作为实验组备用；在另一台计算机中，安装优化前时滞系统应用程序，并将其作为对照组备用.实验开始前，可按照下表完成实验参数设定.

3.1 实验参数设定

表1 实验参数设定表

表1中数据依次代表预估系统稳定性、系统稳定系数、预估人为控制程度、人为可控性系数、时滞现象出现概率、线性时滞周期.为保证实验的公平性，实验组、对照组的参数，始终保持一致.表1中的数据均为理想状态下的理论值，在实际应用过程中，仅能起到参考作用.

3.2 系统应用稳定性对比

根据表1可知，理想状态下优化前后线性时滞系统的应用稳定性，均为87.62%.在保持实验组、对照组系统数据处理总量相同的情况下，分别记录两组系统的真实稳定性，并将测量结果与理想值对比，具体实验结果，由图5、图6所示.

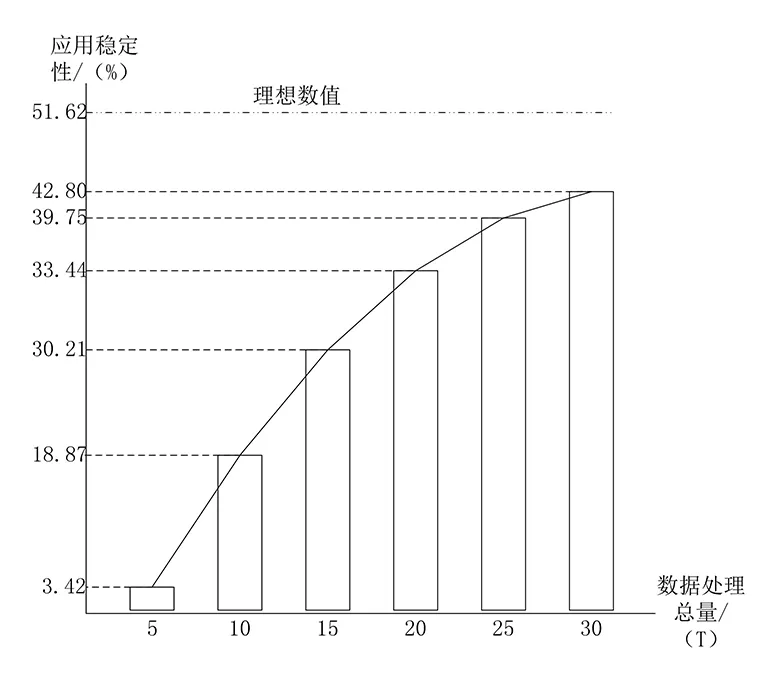
图5 系统应用稳定性(实验组)图

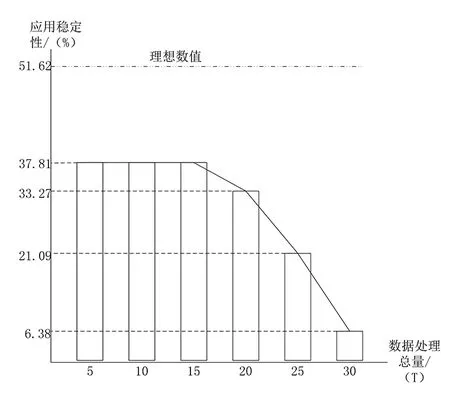
图6 系统应用稳定性(对照组)图

分析图5可知，随着数据处理总量的增加，实验组系统的应用稳定性呈现逐渐增加的趋势，但增加幅度逐渐减小，当数据处理总量为30 T时，实验组系统的稳定性达到最大值42.80%，与理想值间差距为8.82%.分析图6可知，随着数据处理总量的增加，对照组系统的应用稳定性呈现先水平再下降的趋势，且下降阶段的幅度逐渐增大，当数据处理总量保持在5～15 T范围内时，对照组系统的应用稳定性，始终保持在最大值37.81%，与理想值间差距为13.81%，远大于实验组.所以，可证明应用新型时滞系统稳定性优化技术，能够使系统应用稳定性得到近5%的提升.

3.3 系统的人为可控性对比

根据表1可知，理想状态下优化前后线性时滞系统的人为可控性，能够达到67.14%.系统的人为可控性与APR指标间，存在一定的制约关系.随着APR指标的不断增大，线性时滞系统人为可控性呈现逐渐下降的趋势，反之则上升.在保持实验组、对照组系统数据处理总量相同的情况下，分别记录两组系统APR指标的变化情况，并将测量结果与理想值对比，具体实验结果，由图7、图8所示.

图7 系统人为可控性(实验组)图

图8 系统人为可控性(对照组)图

分析图7可知，随着数据处理总量的增加，实验组系统的APR指标，呈现出较为稳定的波动状态，当数据处理总量为1.96 T时，APR指标达到最大值10.84%，与目标值11.04%间差距为0.20%；实验组系统的人为可控性，也呈现出较为稳定的波动状态，当数据处理总量为3.85 T时，人为可控性达到最大值58.05%，与目标值57.41%间差距为0.64%.分析图8可知，随着数据处理总量的增加，对照组系统的APR指标，呈现出较为稳定的波动状态，当数据处理总量为14.03 T时，APR指标达到最大值42.32%，与目标值11.04%间差距为32.28%，远大于实验组；对照组组系统的人为可控性，也呈现出较为稳定的波动状态，当数据处理总量为10.89 T时，人为可控性达到最大值30.00%，与目标值57.41%间差距为27.41%，远大于实验组.所以，可证明应用新型时滞系统稳定性优化技术，能够从根本上加强系统的人为可控性.

4 结束语

通过对线性常时滞系统、线性变时滞系统稳定性优化技术的研究，达到对系统进行人为控制的目的.且实验结果可证明，优化后时滞系统的稳定性，确实得到一定程度的促进.未来将以此次研究作为出发原点，对系统的线性时滞现象，进行更加深入地探索，力求做到逐渐降低时滞现象对系统应用造成的影响，全面提升系统稳定性.