基于灰色马尔科夫模型的郑州市汽车保有量的预测

王玉环，席祥祥

(1.郑州黄河护理职业学院 公共教学部，河南 郑州 450000；2.郑州科技学院 基础部，河南 郑州 450064)

随着中国经济社会持续快速发展，机动车保有量继续保持高速增长态势，汽车消费量的不断增长与有限的道路资源之间的矛盾，使得中国大中城市的道路交通越来越紧张，大量的汽车出行同时给城市的环境带来了巨大的影响[1]. 在此基础上对机动车保有量的预测就显得尤为重要[2-3]，它不但可以为政府制定社会宏观经济发展计划，还能为城市实行节能减排计划提供一定的交通管理措施. 本文根据郑州市2007-2016年的汽车保有量，建立灰色马尔科夫模型，预测郑州市未来三年的汽车保有量.

1 灰色马尔科夫模型的提出

灰色马尔科夫模型是将灰色预测模型与马尔科夫模型结合的方法，先借助于灰色模型对保有量进行预测，再运用马尔科夫模型对预测模型的残差进行改进，从而得到精准度更高的预测结果. 在交通运输业的汽车保有量的问题上，由于受各种因素的综合影响，很难判断出影响其需求量的主要因素或次要因素，因此可以将城市机动车交通看作是信息不全的灰色系统.该模型具备所用信息量少、计算简便等特点，从往年的交通运输数据中探求内在的规律，找寻有用的信息，选定GM(1,1)模型对郑州市的汽车保有量进行预测.

2 灰色马尔科夫链模型的建立

对给定的往年的汽车保有量记为：

x(0)=[x(0)(1),x(0)(2),…，x(0)(n)].

(1)

对原始数据进行累加，记一次累加生成数列为：

x(1)=[x(1)(1),x(1)(2),…，x(1)(n)].

(2)

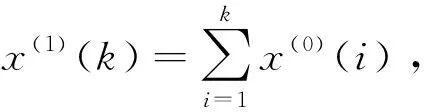
(3)

以x(0)(k+1)表示离散形式的微分项，x(1)取k和k+1时刻的平均值，则

(4)

(5)

将上述的计算过程用矩阵形式表示，则有

(6)

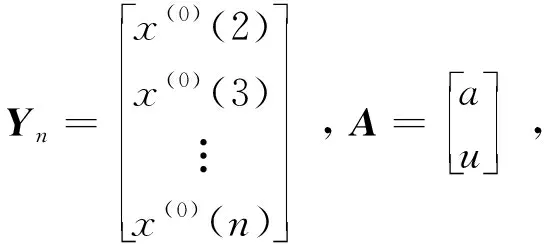
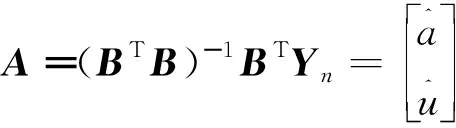
(7)

那么离散形式为：

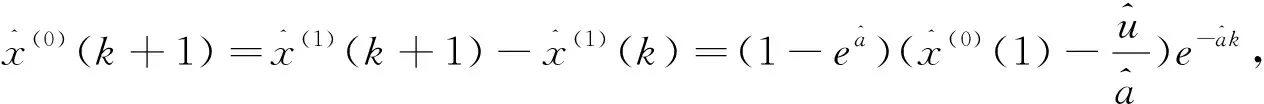
(8)

上述式子即为GM(1,1)模型的时间响应函数模型.

在灰色预测的结果下，运用马尔科夫模型对预测结果进行改进，得到的数值会更为精确. 马尔科夫链的基本思想是通过原始数据序列求得序列的状态转移矩阵，根据状态转移矩阵对未来的变化趋势做出估计，一步状态转移矩阵形式为：

式中，Pij为由马尔科夫链状态Si转移到状态Sj的概率.

3 灰色马尔科夫链预测模型的应用

3.1 灰色模型预测

将郑州市2007-2016年的汽车保有量作为预测对象，运用灰色马尔科夫链模型进行预测，利用Matlab7.0软件计算可得到灰色预测模型如下：

(9)

令x(0)(1)=40.3，即可预测出后几年的汽车保有量，经计算可得郑州市2007-2016年汽车保有量的拟合值及两者的相对误差见表1

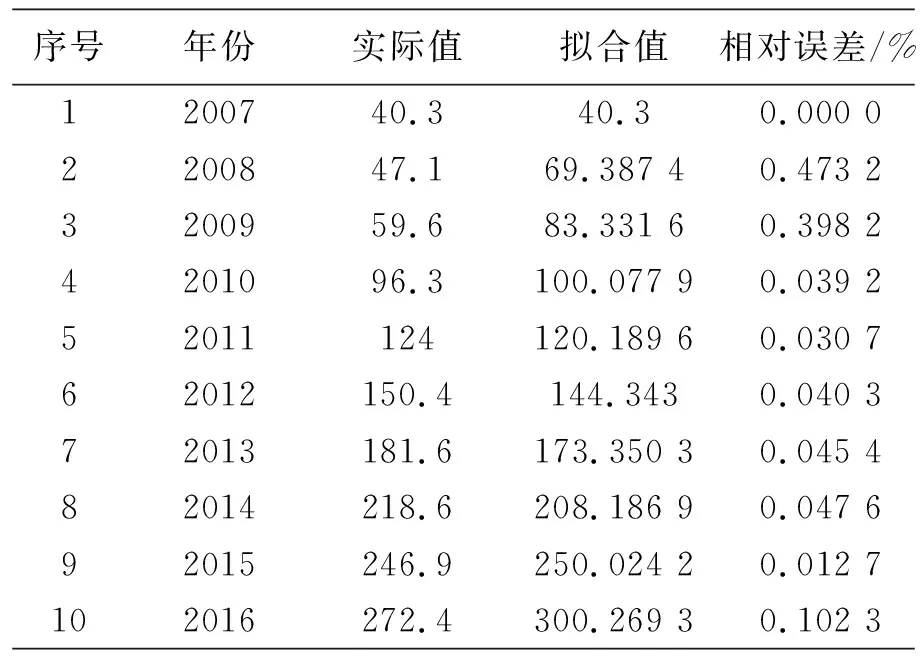
表1 郑州市2007-2016年汽车保有量及拟合值

图1 郑州市2007-2016年汽车保有量实际值与拟合值

建立模型后，进一步对模型精度验证，算出模型的后验差比值C为0.118，对应的小误差概率P为0.9，根据预测模型小误差概率和后验差比值的综合评定标准，模型预测精度为一级，模型预测比较好，通过图1可以反映出拟合的精确度. 并且运用该模型可预测出郑州市2017-2019年汽车保有量见表2.

表2 2017-2019年郑州市汽车保有量

3.2 利用马尔科夫链模型对预测值进行修正

根据相对误差的大小将序列进行划分，所划分的状态如表3所示

表3 郑州市汽车保有量预测的残差划分情况

通过对转移的样本数与原始状态样本数进行比较，可得一步转移矩阵为：

设初始年份的状态为a0=(p01,p02,p03)，那么第k年的值状态是1，2，3的概率为：ak=(pk1,pk2,pk3)Pk.

从上述公式可得到2017-2019年的修正值及状态概率,如表4.

4 结语

本文运用灰色马尔科夫链模型对郑州市汽车保有量进行预测，通过数据修正后，结果更加接近实际情况，也为城市实行低碳交通管理提供一定的思路. 由此可以得出该模型适合随机时间序列类型的预测，与常规的预测方面相比，该方法具有计算简单，精度高的特点. 但在预测过程中没有考虑到其他外部条件的变化，因此该模型在短期内的汽车保有量预测比较有效.

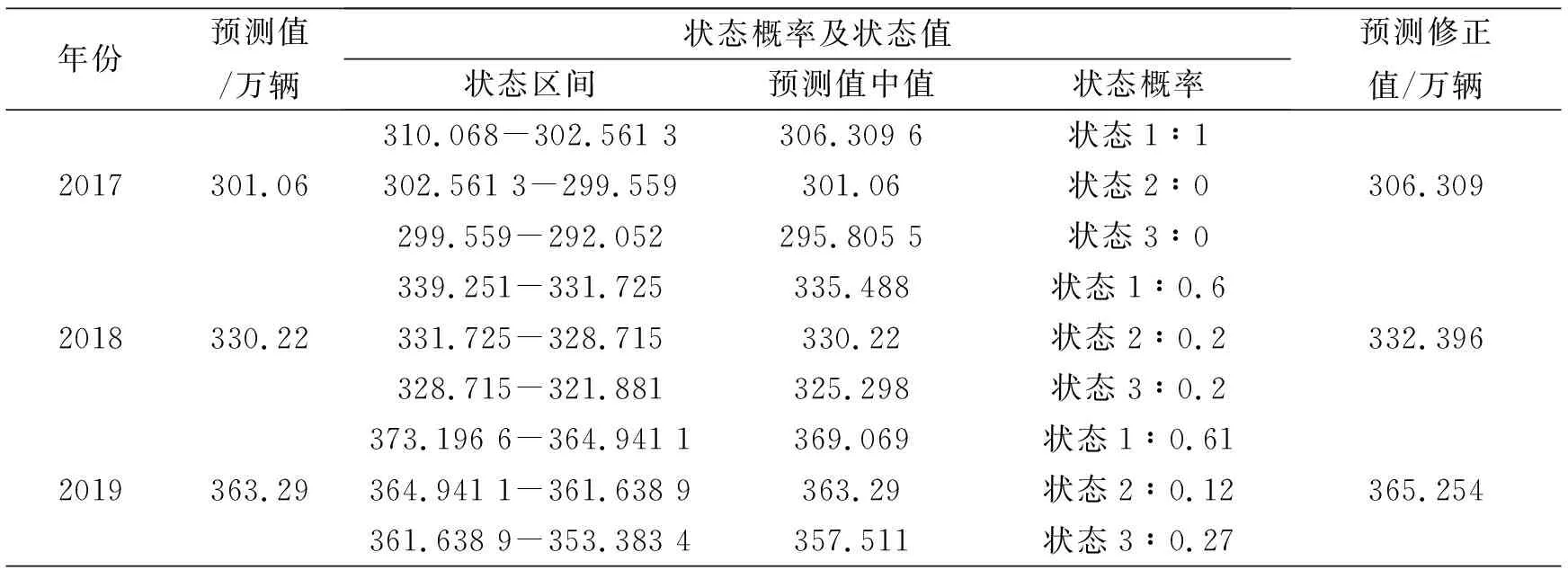
表4 修正值及状态概率