基于卷积神经网络的稳定图自动分析方法

苏 亮， 宋明亮， 董石麟

(浙江大学 建筑工程学院，杭州 310058)

准确获取结构的模态参数是结构健康监测(Structural Health Monitoring, SHM)理论及应用的基础[1]。众所周知，为获得与结构相关的所有信息，在模态参数识别之前，需预设较高的模态阶次。然而，较高的模态阶次将无法避免地引进虚假模态。

正确区分物理模态与虚假模态是模态分析领域存在已久的研究课题[2]。过去20年，在频域和时域模态识别理论中，专家学者提出了很多剔除虚假模态的方法,然而经典方法都倾向于选择合适的系统阶次，并不能区分物理模态和虚假模态[3]。另一方面，在现代模态分析商业软件中使用的模态参数识别算法大多衍生自多项式模型，尽管这些算法存在应用上的微小差别，它们却都可以使用稳定图法区分物理与虚假模态[4]，这使得稳定图法成为该领域使用最广泛的分析方法[5]。

使用稳定图法区分真实模态和虚假模态的容易程度和精确度依赖于传感器监测的数据质量、模态识别理论的稳健性以及分析人员的经验[6]。因而这一过程不仅需要耗费大量的时间精力，且具有一定的主观性，降低了识别的精度。此外，对于大型复杂结构，自由度数目庞大，且在运营模态分析时，要求能够对稳定图进行实时在线分析，以上原因使得人工分析稳定图在运营模态分析中很难实现。因此，如何对运营中的大型复杂结构产生的庞大数量的稳定图进行实时自动分析，并有效剔除稳定图上的虚假模态成为健康监测领域需解决的关键问题之一。

自动分析稳定图的研究主要分为两类：第一类主要通过设定不同的稳定性指标来获得更为清晰的稳定图，促进稳定图的自动分析[7-9]；第二类研究则主要使用模糊聚类等智能算法结合稳定指标来自动搜索真实模态[10-13]。如孙鑫晖等[14]提出了一些自动获取稳定图上真实极点的方法,并对其进行了改进。这些方法或者需要人为主观地设定聚类中心数目，或者需要对提出的稳定指标(或特征)设定阈值，使得这些算法无法真正做到完全自动化。

另一方面，利用稳定图区分真假模态的过程可看成是图像分析的过程，即将稳定图上的点分为代表真实模态和虚假模态两类，因而可以借助计算机视觉理论进行稳定图自动分析。自2006年诞生以来，深度学习[15]在图像识别、语音识别、自然语言处理、计算机视觉等诸多领域取得了巨大成功[16]。深度学习与传统模式识别方法最大的不同在于它能从大数据中自动学习特征，无需人为提取图像中的特征或设定特征阈值。而卷积神经网络作为深度学习中使用最广泛的算法，适用于解决数据量大的图像分析问题，其自动学习到的特征比手工特征或局部特征的分类准确率更高[17]。

基于上述原因，本文提出一种基于卷积神经网络(Convolutional Neural Network, CNN)的稳定图自动分析方法。将稳定图划分成若干个较小的图像块作为CNN的输入，并根据专家识别结果给定每个输入的标签，利用训练好的网络得到稳定图的真假模态的分类结果。用3自由度和7自由度弹簧质量模型的数值算例以及加拿大HCT大楼和瑞士Z24桥振动监测数据对提出的算法进行了验证。实验结果表明，所提方法能够自动学习真实模态的特征，在无需人工提取特征参数，也无需设定任何阈值的情况下，可快速自动地获取结构兴趣频带内的真实模态参数，算法具有较好的收敛性和稳健性。此外，本文搭建的CNN网络亦可应用于其他一般结构的稳定图自动识别。

1 稳定图

稳定图作为一种有效剔除虚假模态的工具，一般包含3类信息：频率f，阻尼比ξ和模态振型φ，这些参数均由假设的不同的系统阶次计算所得。通常，如果所有的3个模态参数均满足如下条件，则认为该点是稳定点

(1)

(2)

MAC表示了2个振型向量之间的空间相关性。众所周知，随着系统阶次n的变化，代表真实模态的极点和代表虚假模态的极点会同时出现在稳定图上，真实极点通常是稳定的，虚假极点则可能不稳定。稳定图正是根据这一原则，将虚假极点从稳定图中剔除。图1显示了一个数值算例的稳定图，从图1可知，当没有噪声干扰时，随着假定模态阶次的改变，代表系统真实模态的极点在固有频率(图1中竖线)处会排成一列，而虚假模态则不会一直存在，表明用稳定图法确定真实模态具有一定的可行性。然而，在实际工程中，由于噪声的干扰以及结构本身的复杂性，稳定图变得相当复杂，人工从稳定图上判断真实模态需要耗费大量时间精力，且容易产生错误。

☆-频率、阻尼、振型都稳定的点；○-频率、阻尼稳定点；-仅有频率稳定的点图1 某数值算例稳定图Fig.1 Stabilization diagram of one numerical example

2 卷积神经网络(CNN)

2.1 CNN的背景与概念

深度学习模拟人脑的网络结构，通过对接收到的信息层层筛选，最终得到对输入信息的认知。它是机器学习的一个重要分支，也是机器学习领域最近的研究热点。CNN[18]是一种用于处理二维输入数据的多层人工神经网络，其作为深度学习使用最广泛的模型，有着良好的容错能力、并行处理能力和自学能力。CNN中的每一层都是由多个二维平面组成，每个平面则由若干独立的神经元组成，相邻两层的神经元互相连接。此外，CNN采用了权值共享有效降低模型的学习复杂度，使之具有更少的网络连接数和权值参数，从而更适应于计算量庞大的图像特征学习与分类。这些优良性能使得CNN能够较好地应用于语言识别、图像识别和自然语言处理等机器学习问题中。

2.2 CNN的基本结构与工作原理

一个典型的CNN模型结构，如图2所示。它主要由输入层、卷积层、下采样层(池化层)、全连接层和输出层组成。

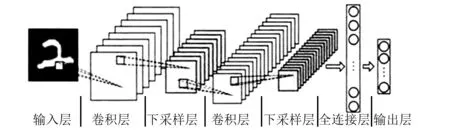
图2 卷积神经网络的结构示意图Fig.2 Schematic diagram of convolutional neural network structure

输入层通常为经预处理后的二维图像X。定义Hi为CNN第i层的特征图。对于卷积层，Hi的计算方式为

Hi=f(Hi-1⊗Wi+bi)

(3)

式中：Wi为第层卷积核的权值向量；运算符号“⊗”为卷积核与第i-1层图像或特征图像进行卷积操作；bi为第i层的偏置向量；f(x)为激励函数。

下采样层依据一定的采样规则[19]对特征图进行下采样，其主要功能是将不同位置的特征进行聚合，从而对特征图进行降维，而在一定程度上保持特征尺度的不变。

经过多个卷积层和下采样层的交替传递，使用全连接层针对提取到的特征进行分类，得到基于输入的概率分布Yi其中li表示第i个训练样本标签的类别。

Y(i)=P(L=li|H0;(W,b))

(4)

CNN的训练方法是使损失函数L=(W,b)最小化。输入H0经过前馈运算后通过损失函数计算出与期望值之间的差异，成为“残差”。常用均方误差(Mean Squared Error，MSE)作为损失函数

(5)

在反向传播阶段，CNN常用的优化方法是梯度下降法，残差通过梯度下降进行反向传播，逐层更新CNN的各个层的训练参数(W和b)，从而得到训练好的CNN。

CNN训练完成后，便可对测试样本进行预测，即将输入数据通过训练好的网络进行前馈运算，在各个层次上输出特征图，最后利用全连接网络输出基于输入数据得条件概率分布，从而达到对样本分类的目的。

3 基于CNN的稳定图自动分析

3.1 将稳定图分析转化为CNN图像分类问题

由于CNN的适用条件是对大量图像进行分析，而单一的稳定图无法应用CNN。因此，本文提出构建如图3所示的仅代表真实模态或虚假模态的单一模态稳定图(Single Mode Stabilization Diagram, SMSD)，作为CNN的输入样本，即一张700×900像素的二维图像。具体做法是，以一定的频率宽度bf将稳定图划分为若干个长矩形条，其中bf由频率识别精度确定。每一个矩形条包含若干个极点，这些极点被归为一类，代表一个真实模态或者虚假模态，如图3所示。随着模态阶次的增加，极点整齐地排为一列，因此图3代表了一个真实模态。相反，在图4中，随着模态阶次的变化，在同一频率处仅有少量的极点排为一列，因此图4代表了虚假模态。通过对照专家识别的结果，即可给出每个SMSD的输出标签，分别用yphysical和yspurious表示真实模态和虚假模态。

yphysical=[1 0]T,yspurious=[0 1]T

(6)

图3 真实模态的单一模态稳定图Fig.3 Single mode stabilization diagram of physical mode

图4 虚假模态的单一模态稳定图Fig.4 Single mode stabilization diagram of spurious mode

3.2 对CNN输入样本进行预处理

因为在相同的参数下，图像分辨率越大，通过卷积和采样得到的特征数目就越多，而训练时间和测试时间就越长。为了提升运算速率，并降低无效信息对图像特征学习的干扰，本文在输入样本原有信息的前提下，将原有的SMSD的像素从700×900降低到了200×150，如图5所示。

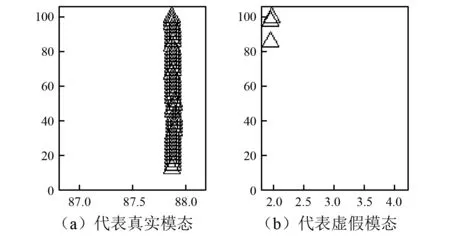
图5 缩小像素后的单一模态稳定图Fig.5 Single mode stabilization diagram after zooming out

另一方面，CNN需要成千上万的输入样本进行训练，因此需要对样本数进行扩充。在滤除空白部分以后，结合兴趣频带的范围以及识别频率的精度要求，设定合适的频带宽度bf，如0.02 Hz。随后，将如图1所示的稳定图上的稳定点归类到每个频带内，归类的原则是：每一类内频率相差的最大值不大于频带宽度值，即可得到若干个包含不同数量稳定点的矩形条，从而获得一定数量的SMSD。由于CNN对于图像位置变换和轮廓变化具有较高的敏感性，采用变换标签法和平移法扩充样本数量，如将“△”改为“☆”和“○”等。同时采用变换结构环境激励的方法，最终得到接近1万

个训练样本。在样本扩充过程中，采用正负例均衡化方法人工增加样本的数据量，避免因样本分布不均导致过拟合现象而降低分类准确率。将扩充得到的训练样本打乱，取80%作为训练集，20%作为测试集，训练集和测试集在图像内容上是绝对隔离的。

3.3 构建CNN模型

网络模型的构建需结合训练样本的数据量以及样本数据的特点，以此确定网络深度、网络每一层的功能以及网络中的超参数，如学习率η等。研究表明[20]，CNN应用于图像分类时有以下规律：①如果训练数据集越大越复杂，网络的深度就越深；②后面的卷积层所取特征数目通常比前面的卷积层多；③输入图像的分辨率越大，所取的特征数目越多，下采样层的抽样矩阵也越大；④CNN的下采样层数通常不超过3层。

结合以上规律，考虑到SMSD样本本身较简单，且样本训练数据量仅需数千的级别就可训练得到有效的CNN模型。因此，针对输入大小为200×150的灰度图SMSD(彩色维度为1)分类问题设计一个6C-2S-12C-5S的CNN模型，如图6所示，其中C表示卷积层，S表示下采样层；数字表示相应层所取特征映射个数；其中第一个卷积层的卷积核大小设定为5×5，第二个卷积层的卷积核大小设定为4×4。

图6 卷积神经网络模型结构图Fig.6 Schematic diagram of convolutional neural network structure

以图6为例，说明本文设计的CNN特征提取的过程。首先输入像素为200×150 的SMSD 图像通过第一个卷积层(C1)在特征空间重构，获得6个特征图像，每个特征图像大小为196×146，根据C1层卷积核大小为5×5，其计算方式为

(200-5+1)×(150-5+1)=196×146

(7)

经过下采样层S1的池化作用后，大小为(196/2)×(146/2)=98×73的特征图像。同理，经过卷积层C2后，特征图像大小变为95×70；经过下采样层S2后，特征图像大小变为19×14，因此，全连接层得到的特征向量长度为19×14×12=3 192。

3.4 使用CNN模型预测真假模态

反向传播阶段，设定学习参数，采用梯度下降法对CNN进行训练，得到训练好的CNN。经过激活函数计算得到预测的标签值，从而进行真假模态的分类。

激励函数是CNN的核心部分之一，常用的两种函数有Sigmoid(x)函数和双曲正切tanhx函数，如图7所示。在进行计算对比之后发现，对于SMSD的识别，Sigmoid(x)函数收敛性优于tanhx函数，因此本文采用Sigmoid(x)函数作为激励函数。

(8)

(9)

此外，在网络模型初始设置中，如权重设定过高，则Sigmoid会饱和，导致死神经元(Dead Neurons)，如果权重太小，梯度值也会很小。因此，需要在中间区域选择权值。根据已有关于初始权值的研究[21]，可将该层卷积核每个元素初始化为式(10)之间的随机数，如式(10)所示

(10)

式中：Fin为该层输入维度；Fout为该层输出维度。

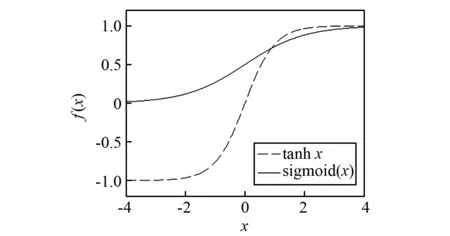
图7 不同激活函数的函数图像Fig.7 Graphs for different activation functions

4 算例分析

为验证本文所设计的CNN自动分析SMSD剔除虚假模态的有效性和对于不同结构稳定图自动分析的通用性，编制了随机子空间法模态识别的Matlab程序，分别计算出3自由度数值模型、7自由度数值模型、HCT大楼、Z24桥4个结构的稳定图，并通过预处理得到相应的SMSD训练样本和测试样本，随后输入构建好的CNN模型进行训练和测试。每个算例的介绍及稳定图的获取过程，如图8所示。

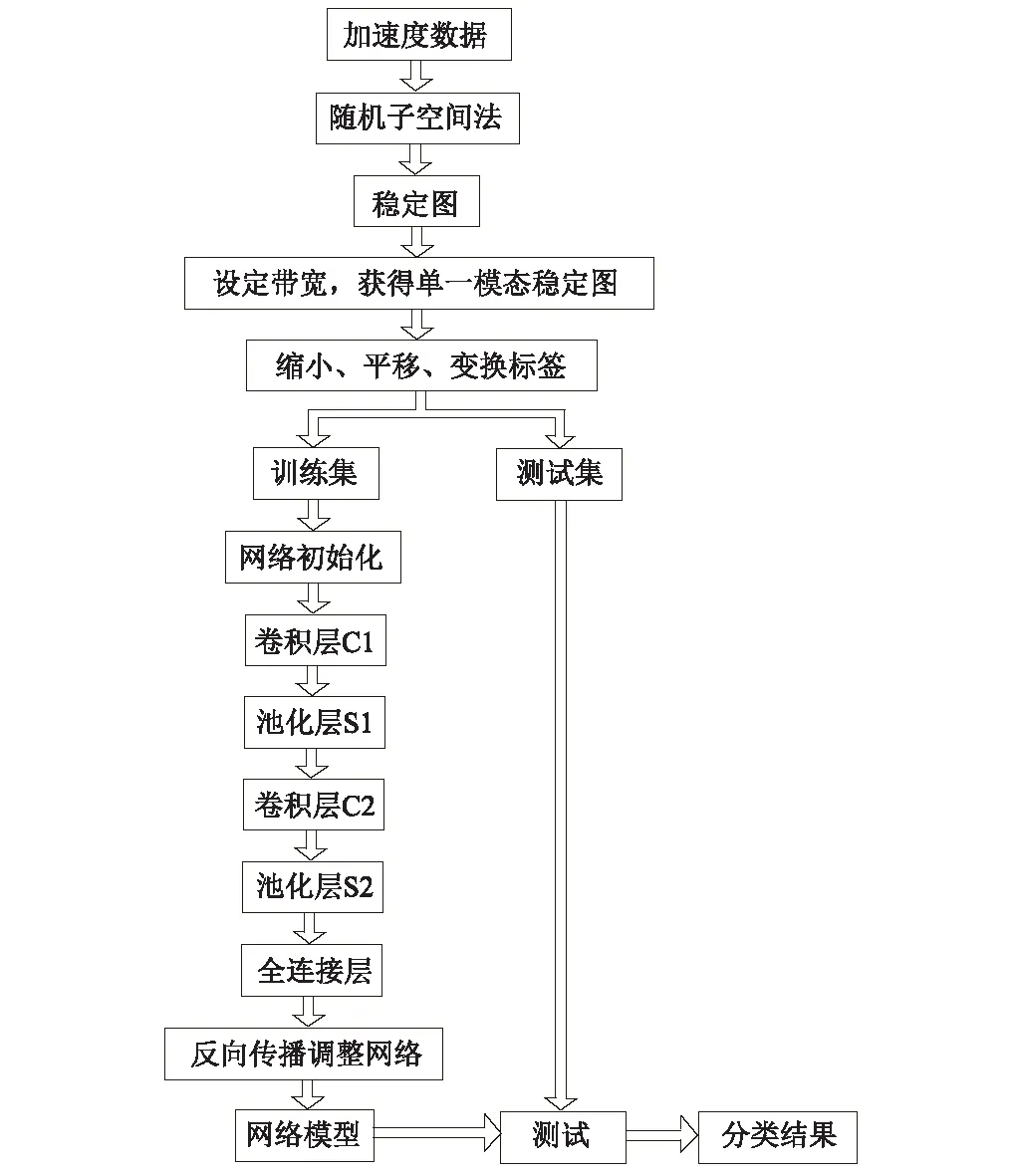
图8 卷积神经网络自动分析稳定图流程图Fig.8 Flow chart of automatically analyzing stabilizationdiagram with convolutional neural network

4.1 3自由度弹簧质量模型

3自由度弹簧质量模型[22]由Matlab软件建立，其中系统的质量矩阵、刚度矩阵分别为

(11)

由此，可计算得到固有频率为：2.82 Hz，7.49 Hz，10.93 Hz。

在每个质量点上施加白噪声激励，设定采样频率为100 Hz，将采集得到的加速度数据代入随机子空间法程序，即可计算得到稳定图，如图9所示。

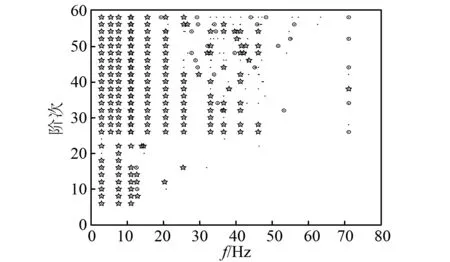
图9 3自由度模型稳定图Fig.9 Stabilization diagram of 3 DOF model

4.2 7自由度弹簧质量模型

同样采用Matlab软件建立一个7自由度弹簧质量模型[23]，其系统的质量矩阵、刚度矩阵分别为

[M]=I(7, 7)

(12)

(13)

设阻尼比为

[C]=0.2[M]+0.000 3[K]

(14)

通过特征值分解，可得理论模态的固有频率为：13.39 Hz，22.85 Hz，28.17 Hz，28.87 Hz，40.15 Hz，41.39 Hz，46.90 Hz。

同理，设定采样频率为1 000 Hz，由随机子空间法计算得到的稳定图，如图10所示。

4.3 加拿大HCT大楼

以加拿大一所运营中的钢筋混凝土结构大楼(Heritage Court Tower, HCT)为研究对象，采用英国哥

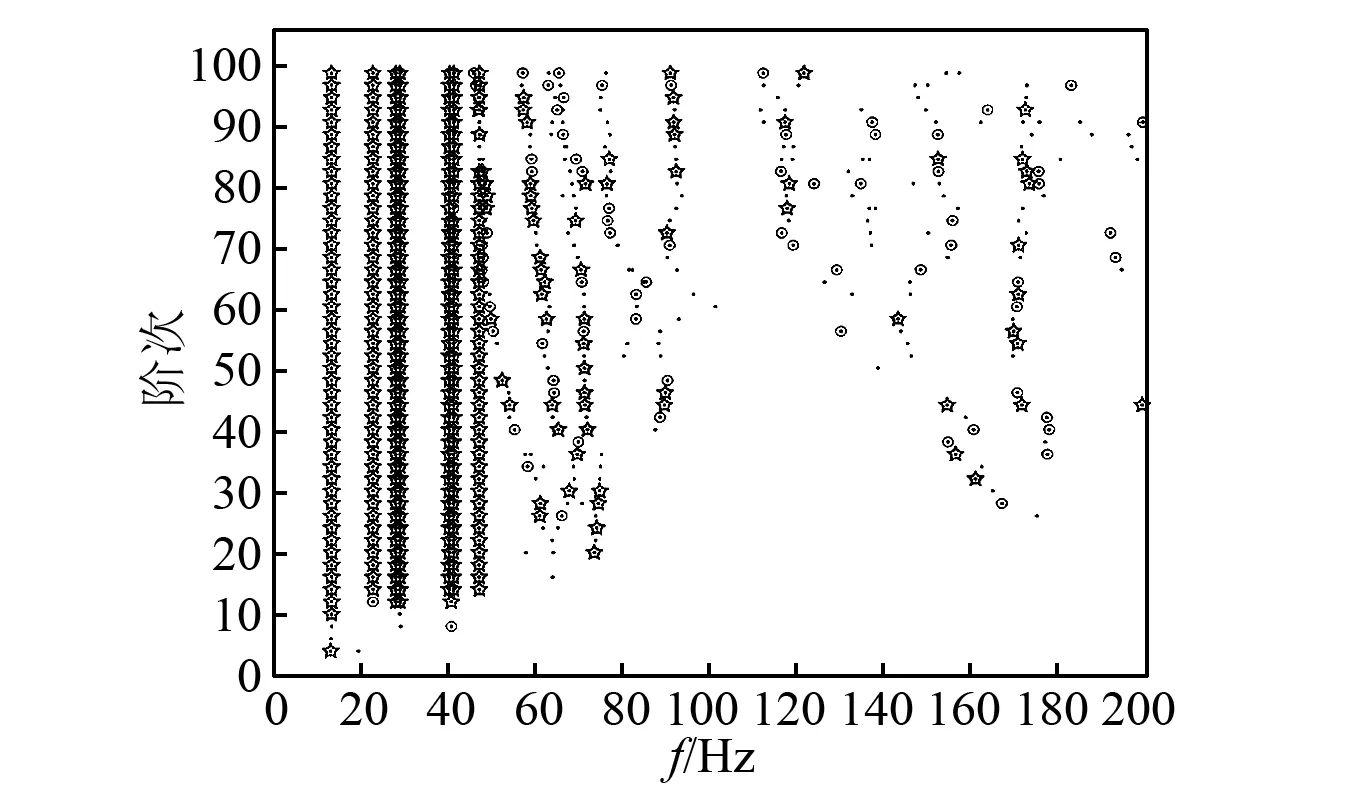
图10 7自由度系统稳定图Fig.10 Stabilization diagram of 7 DOF model

伦比亚大学Felber研究团队采集的环境激励振动加速度数据计算得到该结构的稳定图。所采用的测试数据共有为4个分布，其中第1分布包含6个通道，其他分布各有8个通道，每个通道包含13 108个加速度数据，采样频率为40 Hz。随机子空间法计算得到稳定图如图11所示。

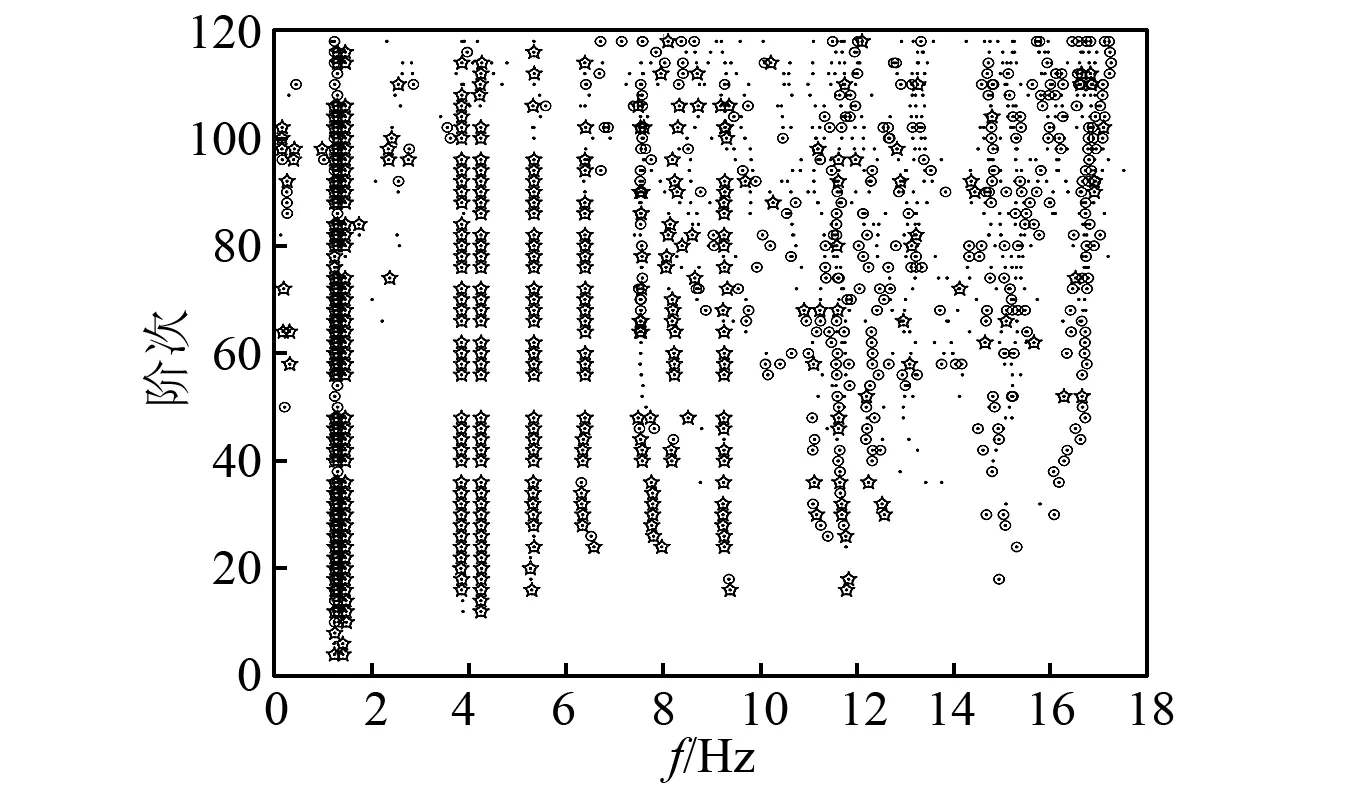
图11 HCT大楼稳定图Fig.11 Stabilization diagram of heritage court tower

4.4 Z24桥及振动数据简介

瑞士Z24[24]桥位于瑞士伯恩州，是一座单箱双室形式的预应力混凝土箱梁桥。其主跨30 m，两边跨均为14 m。本文使用的Z24桥加速响应数据来源于丹麦SVS公司。监测一共分为9个分布，每个分布有33个通道，其中28个通道位于桥面，3个位于桥面的参考点通道，2个为桥墩测试通道共5个固定通道作为参考点，每个通道数据长度均为21 839，采样频率为33.33 Hz。由随机子空间法计算得到的稳定图如图12所示。

4.5 CNN模型训练及测试

将上述4个算例计算得到的稳定图经过前文所述的预处理方法进行处理，得到9 500个SMSD，并以8 000个样本(其中4 000个为真实模态，4 000个为虚假模态)作为训练集，1 500个样本(其中690个为真实模态，810个为虚假模态)作为测试集。每个样本的期望标签由数值计算的理论值和专家人工识别的真实模态确定。采用本文构建的“6C-2S-12C-5S”卷积网络模型进行训练，学习率设定为0.1，迭代次数设为50。经过训练，得到的损失函数随训练次数变化曲线，如图13所示。由图13可知，本文设计的CNN能够在无需人为设定特征参数的情况下，自动识别稳定图上真假模态的特点。经过50次迭代以后，损失函数即由45.75下降到了0.32，平均每训练一次，可下降1.98%。

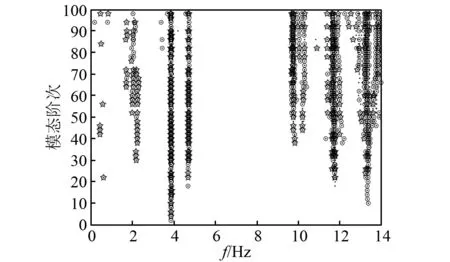
图12 Z24大桥稳定图Fig.12 Stabilization diagram of Z24 Bridge

图13 损失函数随训练次数变化图Fig.13 Training lose-epoch curve

将测试集中包含的1 500个样本代入训练好的CNN进行测试。测试发现错误率仅为0.267%，仅错误4个，说明本文所提出的算法能够很好的区分稳定图上的真假模态。此外，识别错误的样本号分别为：137，270，386，1 405，其中某一识别错误的SMSD，如图14所示。

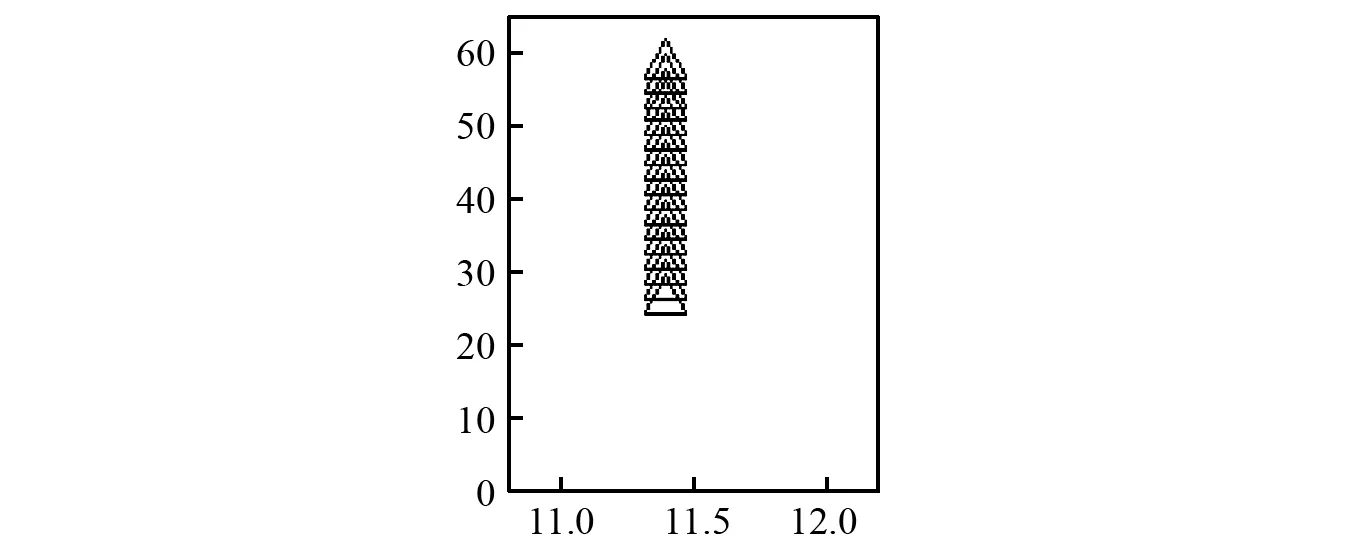
图14 识别错误的单一模态稳定图Fig.14 Wrong examples of single mode stabilization diagrams

与专家识别结果对比发现，实际上这4个SMSD都是同一个SMSD变换而来，且都是将虚假模态识别成了真实模态。这是因为虚假模态常常出现在高阶部分[25]，虽然这一模态有部分极点也排成了一列，但是在阶次为0～24内，并没有极点存在，因而造成了一种类似真实模态的“假象”。为避免这样的错误，保持网络模型其他参数不变，将训练次数提升到100次，损失函数由45.75降低到了0.11，测试准确率即达到了100%。

最后，将预测为真实模态的单一模态稳定图列出，并取其平均值作为该阶真实模态的识别结果。4个算例的识别结果，如表1～表4所示。由识别结果发现CNN可用于自动识别真实模态和虚假模态。

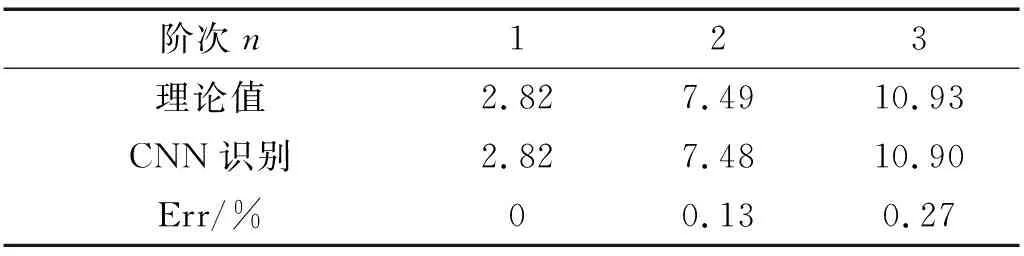
表1 3自由度CNN自动识别与理论值的结果比较

表2 7自由度CNN自动识别与理论值的结果比较

表3 HCT CNN自动识别与专家识别结果比较

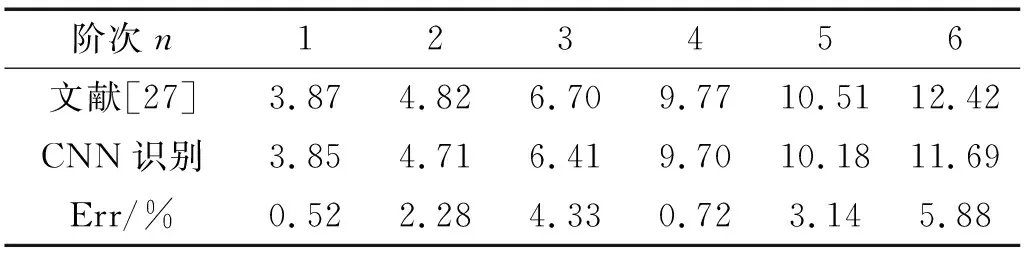
表4 Z24CNN自动识别与专家识别结果比较

5 结 论

本文结合稳定图理论和卷积神经网络理论，提出了一种自动剔除稳定图中虚假模态的新方法。采用数值模型算例和真实结构实测数据将提出算法自动识别模态参数的结果与专家人工识别结果进行了对比，验证了算法的可靠性。在试验过程中，得出了以下结论：

(1)样本量充足的前提下，提出的基于CNN的稳定图自动识别方法能够有效自动地区分稳定图上的真实模态与虚假模态；

(2)搭建的CNN可用于识别不同结构的稳定图，具有一定的通用性，可推广应用于模态分析软件中；

(3)在搭建CNN过程中，试验发现针对SMSD的自动分类，Sigmoid激活函数具有较好的收敛性；通过计算发现当学习率取值为0.1，训练次数取值为100时，具有较好的识别效率和精度。