含单面限位局部非线性结构的主频响应分析
孙 樱, 万雨婷, 陈力奋, 郭其威
(1. 复旦大学 航空航天系,上海 200433;2. 上海市空间飞行器机构重点实验室,上海 201109)
间隙和限位是实际工程结构中常见的、典型的非线性形式,常见的有铰间隙、齿轮间隙等,如大型网架式可展空间结构中有许多含间隙的运动副,可能导致空间结构展开时的非线性振动、磨损以及结构各部分展开不同步等问题[1];限位则往往是考虑安全或功能需求而对物体运动过程中的位置进行了约束,如为了防止桥梁上部结构在地震中发生落梁破坏而在伸缩缝处安装的限位装置[2]。大量研究表明,系统中的间隙或限位对结构动力学特性影响显著[3-5]。
含间隙结构动力学分析主要涉及间隙内碰撞过程的处理和整体结构动力学方程的求解。目前,根据结构部件相对运动关系的假设不同,可以将间隙内碰撞过程归结为四类模型[6]:连续接触模型、有限元模型、经典碰撞模型和接触变形模型。Hertz基于接触变形模型,对于能量耗散只考虑变形位移和变形速度的综合作用,针对碰撞接触面较小的静态接触问题,提出了将间隙内碰撞过程的动力学效应近似地等效为分段线性的非线性模型。考虑到限位约束的结构特征,国内外学者一般也将其简化为分段线性系统,如厉行军等[7]将隔振装置中的限位器简化为带限位的单自由度单层隔冲系统。
对于系统中含有分段线性等非线性元件的结构动力学方程,线性理论中的模态分析法或谱分析法不能适用,一般只能采用半解析方法或数值方法。常见的半解析方法有谐波平衡法、描述函数法、Volterra级数法[8]等。Maezawa等[9]首先将谐波平衡法应用于分析单自由度分段线性问题;Shaw等[10]将带限位器的小车运动简化为分段线性单自由度系统,运用映射手段获得了系统的周期解析;Moussi等[11]对带双边限位器的倒立摆系统用谐波平衡法和渐近法得到正弦激励下的相图,研究了第一、第二阶共振频率同激励幅值的关系;吴志强等[12]将弹性碰撞振动系统简化为对称的分段线性模型,运用平均法求得幅频特性与相频特性,基于约束分岔理论对系统进行稳定性分析。数值方法则能够精确地提供时域和频域的信息。卢绪祥等[13]建立了含对称间隙结构的碰撞振动动力学模型,采用Runge-Kutta法数值求解,碰撞振动系统随着频率比、激振力幅值和间隙的改变,出现了周期、倍周期和混沌运动;Onesmus等[14]研究了不同接触力模型下的含两间隙的平面刚体结构的动力学特性;林道福等[15]给出了带有限位器的浮筏隔振系统在局部坐标系下的刚度矩阵表达,用纽马克积分法计算结构在基础冲击激励下的运动响应。半解析法的特点在于计算效率快,但如果结构过于复杂,一般难以得到其理论解形式;而数值解法对各种结构运动均可计算,但耗时较长,对相关参数的选取较为困难。
综合国内外学者的研究成果,对系统中含有分段线性非线性元件的结构,目前的研究主要还是局限在单自由度或者少自由度系统,针对一般的有限元模型的分析方法尚不成熟。本文主要对于含单面限位分段线性模型的局部非线性结构的主频响应分析方法展开研究,采用描述函数表征单面限位非线性元件的频域特性,基于迭代的逆阵更新方法快速求解大型多自由度结构的主频响应,通过与实验结果的比较,验证本文所提出分析方法的有效性。
1 基于描述函数的逆阵更新方法
受周期性谐波激励的含有限个非线性元件的局部非线性结构振动微分方程为
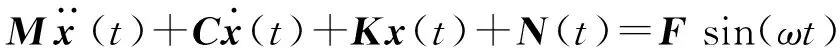
(1)
式中:N(t)为结构中的非线性内力向量。由于非线性内力的存在,使得式(1)所示的非线性系统频响特性和激励方式、激励幅值有关;系统响应可能包含激励频率以外的谐波成分,且振动能量在这些频率上的分布情况和激励幅值密切相关。本文采用描述函数对非线性内力进行频域特性表征,针对局部非线性结构利用迭代的逆阵更新方法进行非线性频响的快速计算。
1.1 非线性内力的描述函数表示
非线性内力向量N(t)中的第k个分量Nk表示节点k与节点j之间的非线性内力在第k个自由度上的分量nkj之和,即
(2)
式中:k=1,2,…,N;j=k为一端接地情形。如式(1)所示的非线性系统受周期性谐波Fsin(ωt)激励时,设其试探解为
x(t)=Xsin(ωt+θ)
(3)
节点k与j之间的频域相对位移Ykj为
(4)
式中:Xk为节点k的频域位移响应。
将式(3)所示的试探解代入式(1),可知各非线性内力形如nkj=nkj(sinωt,cosωt),将其展开成简谐形式
(5)
含有限个非线性元件的局部非线性结构一般关注其主频响应,其对应的非线性内力也仅取其基频项,即
nkj≃Akj(X,ω)sin[ωt+φ1(X,ω)]=Akj(X,ω)sinψ(6)
式中:ψ=ωt+φ1,将Akj(X,ω)用傅里叶积分表示
(7)
令
Dkj(X,ω)
则有
(9a)
(9b)
式(8)所定义的Dkj(X,ω)即为文献[16]中所示的非线性控制中的描述函数,若已知节点k与节点j之间的非线性内力,则可由式(9a)和式(9b)计算描述函数Dkj(X,ω)。由式(8)不难发现,描述函数Dkj(X,ω)是节点k与节点j之间,一个周期内的平均非线性内力与相对位移之比,相当于等效线性刚度
为了评价等效线性系统式(6)和原非线性系统式(5)的贴近程度,引入误差函数
(10)
当系统式(1)受到Fsin(ωt)={Fk(t)}激励时,由文献[17]可知,当且仅当
φfkj nkj(τ)=φfkj nkj,lin(τ)
(11)
成立时的等效线性系统式(6)才能使式(10)所示的误差E取值最小。式(11)中φ为相对输入fkj(t)=Fk(t)-Fj(t)与非线性内力nkj(t)的互相关函数
(12)
不难验证,系统式(1)受到Fsin(ωt)激励时,式(5)所示的原非线性内力与式(6)所示的等效非线性内力满足式(11),由此表明,式(6)为最优准线性化系统。
对于结构中第k个自由度存在如图1所示的单面限位非线性约束的系统,忽略摩擦及碰撞接触时的动量和能量损失,非线性内力nkk由质量块与限位弹簧接触前后刚度系数发生突变的非光滑因素而导致,可简化为图2所示的双线性模型,其中δ为间隙宽度,k1为接触前刚度,接触后刚度则为k1+k2,满足
(13)
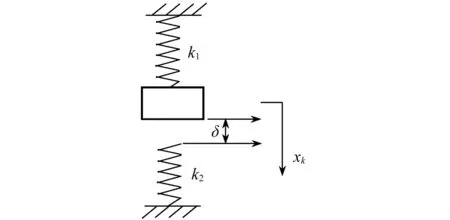
图1 单面限位示意图Fig.1 Diagram of single-sided limitation system
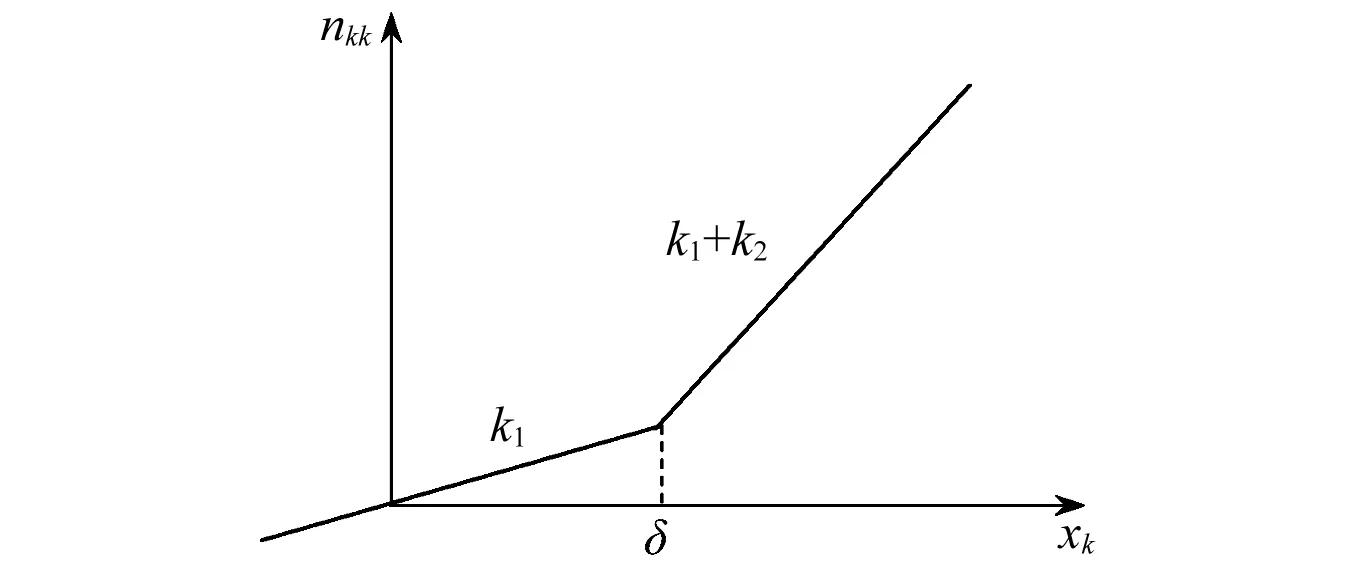
图2 单面限位非线性模型Fig.2 Characteristic of nonlinear internal force
由式(9a)和式(9b),可得单面限位非线性内力nkk(t)的描述函数为
此即等效非线性内力nkk(t)满足式(8)的频域表征。
1.2 逆阵更新方法(Inverse Matrix Update Method, IMUM)
将式(3)代入式(1),考虑到式(2)和式(6),则结构的振动微分方程式(1)可以化为
[-ω2M+iωC+K+Δ(X)]·X(ω)=F
(15)
其中非线性内力向量N(t)的频域幅值向量
G(X,ω)=Δ(X)·X(ω)
(16)
当结构仅含有限个非线性元件时,如在节点k处存在接地非线性元件,在节点i和j以及节点m与n之间存在非线性元件,则Δ(X)矩阵具有如下稀疏特性
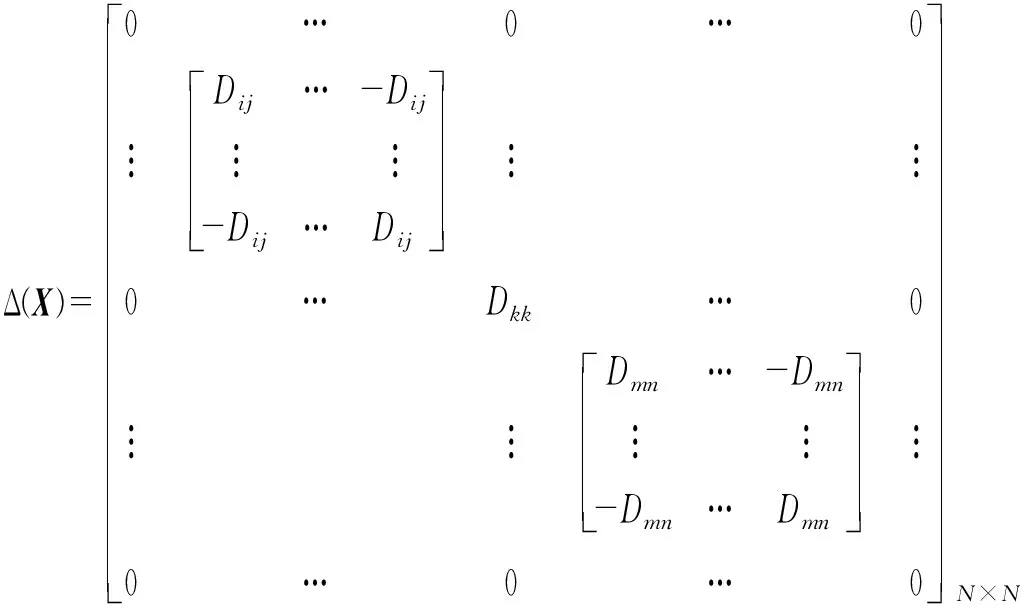
上述Δ(X)可以进一步写成表示非线性元件位置的向量δ以及非线性内力描述函数的低阶矩阵D的乘积
Δ(X)=δ·D·δT
(18)
其中用描述函数表示的非线性程度矩阵
(19)
非线性位置向量

(20)
第i列 第j列 第k列 第m列 第n列
式中:M为系统中非线性元件的个数。记α=(-ω2M+iωC+K)-1为结构中线性部分的动柔度矩阵,令
θ(X)=[α-1+Δ(X)]-1
(21)
称θ(X)为非线性结构的拟动柔度矩阵。利用Sherman-Morrison法则[18],由式(18)可得

(22)
由此即把局部非线性结构拟动柔度矩阵θ(X)的N阶矩阵求逆问题转化为M阶矩阵的求逆。一般来说,局部非线性结构中,非线性元件个数M远小于结构的自由度数N,即M< X(ω)=θ(X)·F (23) 利用式(22)能极大地提高式(23)求解的计算效率,称该方法为逆阵更新方法[19]。 式(23)所示为关于非线性频响X(ω)的非线性代数方程组,将通过构造迭代格式进行求解。为了改善迭代收敛的稳定性,引入加权参数λ,构造Mann迭代[20]格式 X(j+1)(ω)=λ(j)X(j+1)*(ω)+(1-λ(j))X(j)(ω),λ(j)∈(0,1) (24) 式中:X(j+1)*(ω)=θ(X(j)(ω))·F具体算法流程见图3。 图3 逆阵更新的算法流程Fig.3 Flow chart for the computational algorithm IMUM 实际计算结果表明,λ取值越小迭代格式式(24)越容易收敛,但收敛速度越慢;且对于不同的频率点ωi,迭代收敛的差异性较大,如当激励频率接近系统固有频率时较难收敛。为此,采用一种自适应的λ取值算法[21]:如果在频率ωi时迭代不收敛,取λ(j)(ωi)=λ(j)(ωi)·r(其中0 研究如图4所示含单面限位的T字型梁结构,系统由试件、实验平台、激振器、数据控制采集系统、加速度和力传感器组成。试件为一矩形截面悬臂梁,一端用压块固定,靠近另一自由端处有片梁限位;片梁用压块在两端固定;片梁与悬臂梁之间的空隙,构成一个一端接地的单面限位非线性约束。实验中通过调节片梁高度控制限位间隙δ的大小。 图4 含单间隙悬臂梁结构Fig.4 Cantilever beam with single-sided limitation 本节先通过对悬臂梁进行单自由度建模,采用逆阵更新方法(IMUM)求解悬臂梁自由端的位移频响,并与龙格—库塔(RK45)法的计算结果进行比较。 将图4(c)所示悬臂梁简化为单自由度系统,接地端的间隙限位非线性约束模型如图1所示。结构参数为:质量m=0.05 kg,由静力学实验测得分段线性刚度分别为k1=300 N/m,k2=1 200 N/m,取间隙宽度δ=1.4 mm,设阻尼c=0.4 N·s/m;激励为单频简谐激励P=Fsin(2πft),F=0.08 N,f为扫频频率,扫频范围9~16 Hz,扫频间隔0.02 Hz。分别用IMUM和RK45进行由低到高和由高到低两个方向的扫频分析。 采用Runge-Kutta法进行数值计算时采用以下措施: (1)模拟扫频时,在初始频率点处,初始条件为零位移、零初速度;前一个频率点(已达到稳定)最后时刻的运动状态(位移和速度)作为后续频率点的初始条件。 (2)在每个频率点处,截取系统相邻的几段时域响应,比较其幅值的大小,以此判断系统是否已经达到稳定状态。一旦判定系统稳定,就进入下一个频率点。 图5所示为两种方法的计算结果。不难发现,两种方法得到的正向和反向扫频位移频响曲线均表现出明显的跳跃现象:由低到高跳跃点在14 Hz附近,由高到低跳跃点在13 Hz附近;且都有明显的非光滑转折点。 图6所示为两种方法计算结果的比较,结果表明了IMUM方法计算单面限位非线性结构频响特性的有效性。图中峰值附近略有差异,初步分析原因应在于本文的IMUM方法仅考虑了响应中的主频成分。 图5 单自由度单面限位系统位移频响曲线Fig.5 Displacement frequency response of SDOF structure with single-sided limitation 图6 IMUM和Runge-Kutta法系统位移频响比较Fig.6 Displacement frequency response comparison between IMUM and RK4 比较两种方法的计算时间可以发现,在相同计算条件下,RK45耗时2 045.35 s,IMUM耗时0.78 s。显然,在计算精度保证的前提下,IMUM方法极大地提高了非线性频响分析的计算效率。 进一步分析定频激励下的时域响应。选取跳跃点所在区域的频率点13.5 Hz进行定频激励,计算时间长度370.37 s内的位移响应,期间进行4次冲击响应的模拟分析,如图7(b)所示。分别取一段低幅值稳态和高幅值稳态时的时域响应信号(图7(c)和图7(d)),观察到两个显著不同的稳态响应幅值1.19 mm和1.80 mm。由于结构位移幅值超过间隙宽度,运动过程受到单面限位的限制,高幅值响应曲线具有上下不对称性;而结构在反向扫频的该频率点处,位移幅值尚未因接近间隙宽度而发生幅值点的跳跃,表现为低幅值响应曲线上下对称。 图7 双稳态现象Fig.7 Bistable phenomenon 实验采用的是如图4所示的单面限位悬臂梁结构,相关参数见表1。悬臂梁与片梁的接触刚度由重力-位移的静力学试验测得,取1 200 N/m。激励点、响应点和间隙位置距离悬臂梁自由端分别为262 mm,6 mm,30 mm,如图8(a)所示。 表1 悬臂梁相关参数 在ANSYS中建立单面限位悬臂梁模型,采用beam188单元,沿长度方向每10 mm划分一单元,共62个单元;力传感器、加速度传感器、片梁位置的单元号 图8 实验结构多自由度有限元模型Fig.8 Finite element model of experiment structure 分别为36,62和59,如图8(b)所示。加速度传感器质量为10 g,相当于悬臂梁上的一个集中质量,因此结构整体质量和刚度矩阵维数均为372×372。 通过改变单面限位间隙δ、激励力幅值F的大小和不同的扫频方式,研究间隙宽度和激励力对单面限位非线性约束梁结构频响特征的影响。 仿真分析的工况参数与扫频实验一致:①激励力幅值F=0.2 N和0.4 N时的悬臂梁(未接触到片梁)和间隙宽度δ=7 mm时约束梁的频响特征;②间隙宽度δ=7 mm,F依次为1.0 N,1.4 N,1.8 N和2.0 N,对应实验中垫放3片钢尺;③激励力幅值F=0.8 N,间隙宽度δ依次为4 mm,7 mm,10 mm,12 mm和20 mm,对应实验中垫放钢尺片数分别为4,3,2,1和0。 每种工况下,进行由低到高和由高到低两种扫频模式。 考虑单面限位间隙约束悬臂梁中的非线性阻尼,假设线性与非线性阻尼均为跟刚度矩阵有关的比例阻尼:C=αK线性刚度+βM+υK非线性刚度。线性刚度部分对应阻尼不随工况的改变而改变,非线性刚度部分对应阻尼随工况的改变而变化。 由工况①中F=0.2 N和0.4 N时悬臂梁实验测得的频响曲线,可以大致识别出线性比例阻尼系数α=2×10-4和β=0.2。图9为IMUM仿真计算与实验曲线的对比,其中共振频率和幅值:F=0.2 N时为15.2 Hz和3.4 mm;F=0.4 N时为15.2 Hz和7.5 mm,体现出较好的线性性。 工况①间隙宽度为7 mm,对应于实验中垫放3片钢尺,施加外激励力幅值为F=0.8 N时,由约束梁实验测得的频响曲线,可以大致识别出非线性比例阻尼系数υ=4×10-7。图10为IMUM仿真计算与实验曲线的对比,图中的频响曲线特征(共振峰值和幅值的转折点)显示出用IMUM法仿真分析的有效性。 (a) (b)图9 悬臂梁线性比例阻尼识别结果Fig.9 Identification results of the linear proportional damping for the cantilever beam 图10 F=0.8 N,间隙宽度为7 mm的约束梁非线性阻尼系数识别结果Fig.10 Identification results of the nonlinear proportional damping for the cantilever beam with F=0.8 N and δ=7 mm 利用工况①识别出的比例阻尼系数,针对工况②给出的4种激励力幅值情况,计算梁结构的位移频响曲线,IMUM仿真计算与实验结果对比如图11所示。针对工况③给出的5种间隙宽度情况,计算梁结构的位移频响曲线,仿真计算与实验结果对比如图12所示。 从图11可知,随着激励力幅值的增大,结构的频响特征有下述特点: 1)激励力幅值F>0.6 N时,无论是仿真结果还是实验结果,结构的一阶固有频率值和共振峰幅值随着激励力幅值的增加而增大,结构表现出明显的硬弹簧特征; 2)悬臂梁与片梁碰撞后,位移幅值曲线在此处形成拐点,显示出间隙非线性的非光滑特征。 从图12可知,随着垫放钢尺片数的增加,即间隙宽度的减小,结构的频响特征表现为: 1)间隙宽度大于等于10 mm,此时片梁不起作用,结构为悬臂梁; 2)间隙宽度小于7.8 mm,即垫放钢尺片数大于等于3片时,随着间隙宽度的减小(钢尺片数的增加),结构的一阶固有频率值增大,共振峰幅值减小,结构表现出硬弹簧特征; 3)悬臂梁与片梁碰撞后,位移幅值曲线也相应在此处形成拐点。 图11 约束梁从低到高扫频位移幅值曲线,间隙宽度7 mmFig.11 Displacement frequency responses for the T-shaped beam by forward sweep with δ=7 mm 图12 约束梁从低到高扫频位移幅值曲线,F=0.8 NFig.12 Displacement frequency responses for the T-shaped beam by forward sweep with F=0.8 N 选取工况②条件下,即间隙位置固定为7 mm(对应实验中垫放3片钢尺),F依次为0.2 N,0.4 N,0.6 N,1.0 N,1.6 N,2.0 N进行低高和高低两种方式仿真计算,得到不同激励力幅值下的位移幅值曲线见图13。 图13 激励力幅值不同时,从低到高和从高到低扫频的位移幅值曲线Fig.13 Displacement frequency responses for the T-shaped beam by forward and backward sweep with F=0.2 N,0.4 N,0.6 N,1.0 N,1.6 N,2.0 N 由图13可知: (1)激励力幅值F达到0.6 N时,位移曲线出现“跳跃”现象,从低到高扫频与从高到低扫频两条曲线不重合,出现跳跃区间,并且随着激励力幅值的增大,“跳跃”现象越明显,跳跃区间越大; (2)激励力幅值F=0.2 N和0.4 N时,从低到高扫频与从高到低扫频两条曲线基本重合,结构表现为线性特征。 综合图11~图13不难发现,在一定范围内,结构的间隙宽度越小,激励力幅值越大,主梁结构出现频率漂移现象,表现出的硬刚度特性越明显。单面限位的存在,使结构的频响曲线出现明显的“跳跃”现象,呈现非线性振动的双稳态特性。 本文基于描述函数和逆阵更新方法对含单面限位局部非线性结构进行基频响应分析。单自由度模型计算中,通过与RK45数值方法的对比,显示出IMUM迭代算法的高效性和准确性;在多自由度有限元模型基频响应分析中,通过非线性阻尼系数的识别,单面限位约束梁的IMUM仿真分析与实验结果呈现了较好的一致性。分析结果表明,外激励幅值的增加和间隙宽度的减小对结构动态特性的影响有着相似的规律,都会使约束梁结构出现频率漂移现象,表现出越来越硬的刚度特性;间隙限位的存在,使结构的频响曲线出现明显的“跳跃”现象,呈现非线性振动的双稳态特性。1.3 非线性频响的迭代求解
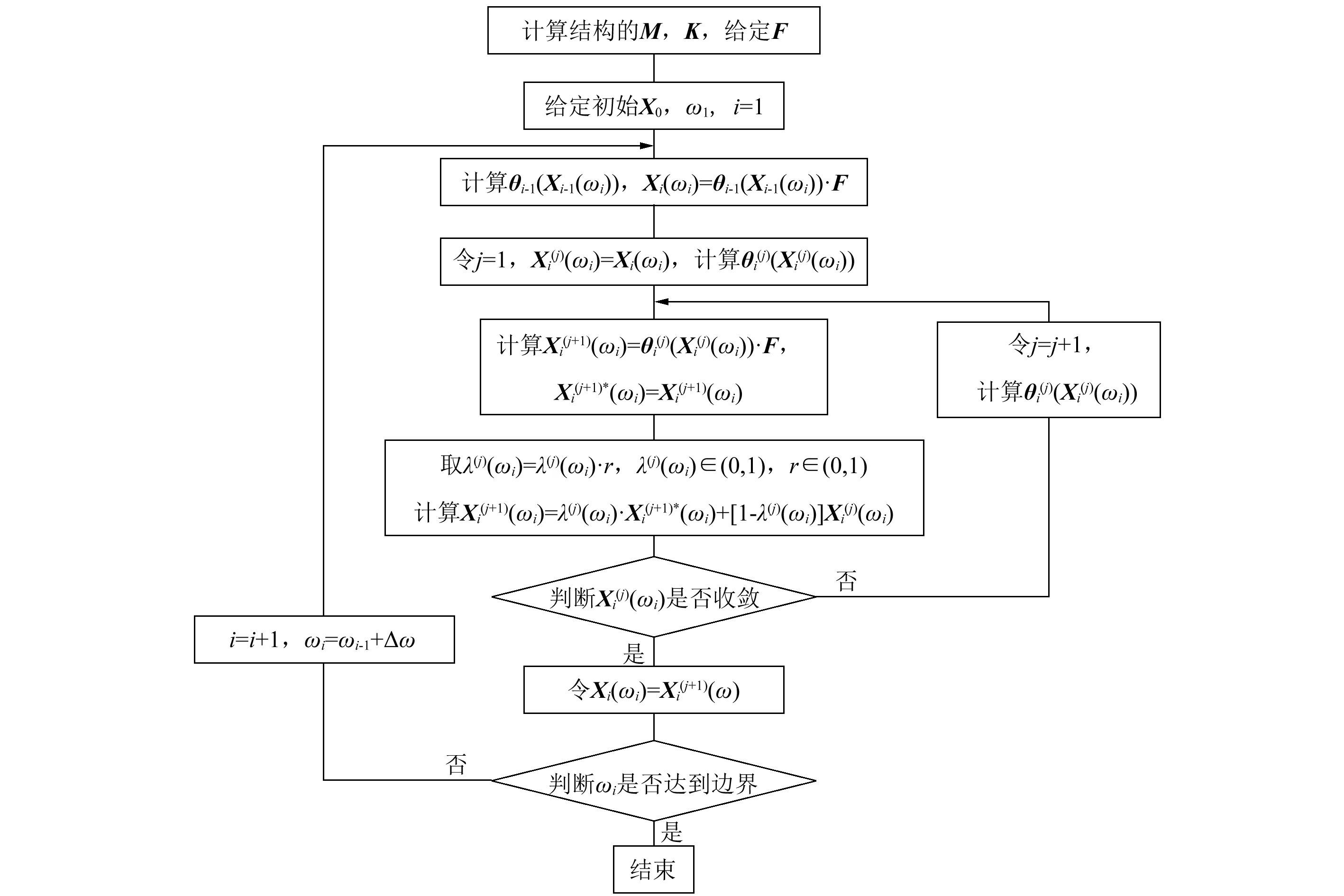
2 单面限位单自由度系统的仿真研究

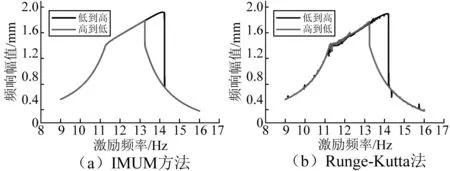
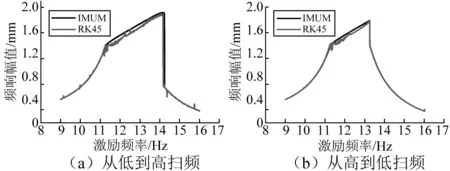
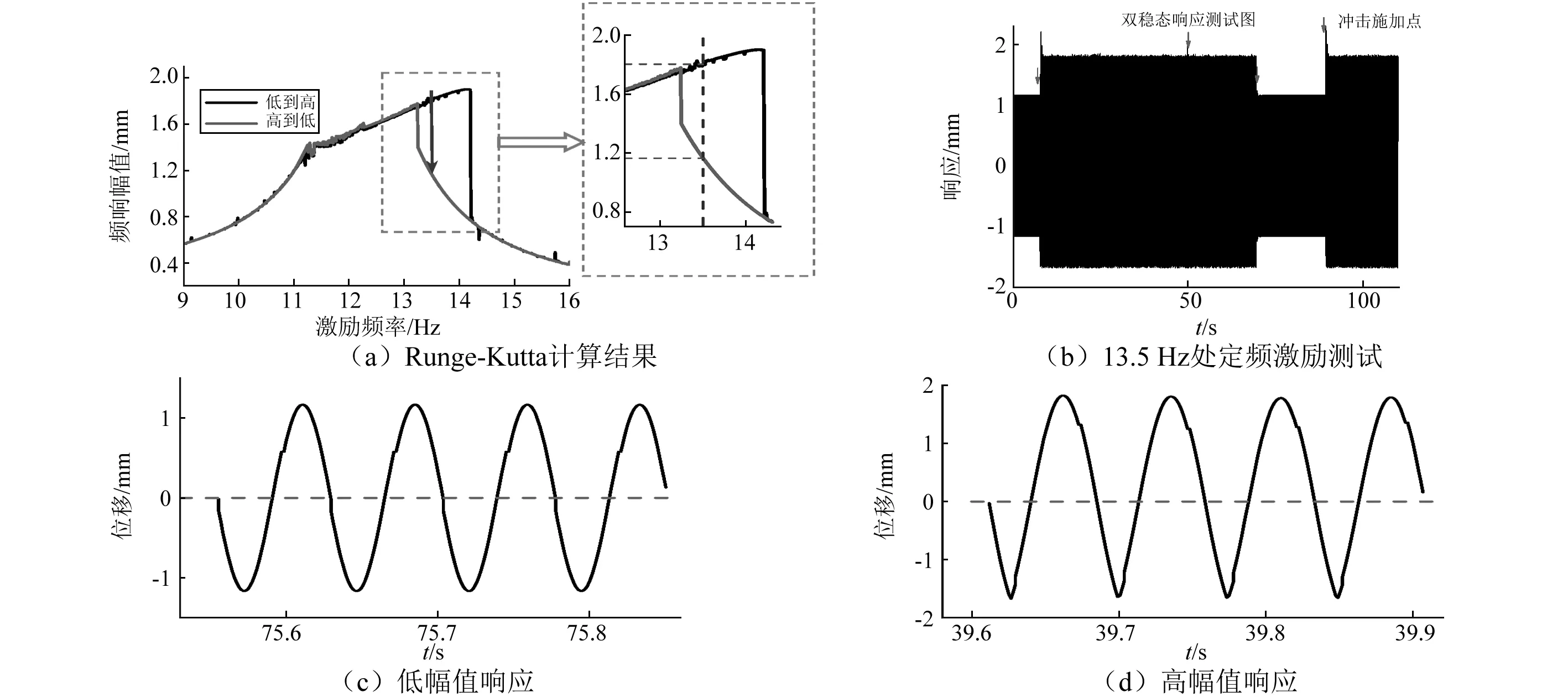
3 含单面限位的悬臂梁多自由度结构频响分析

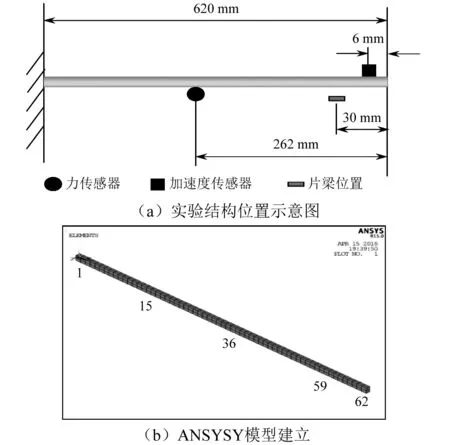
3.1 非线性阻尼识别

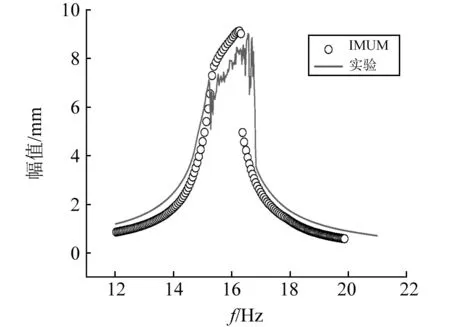
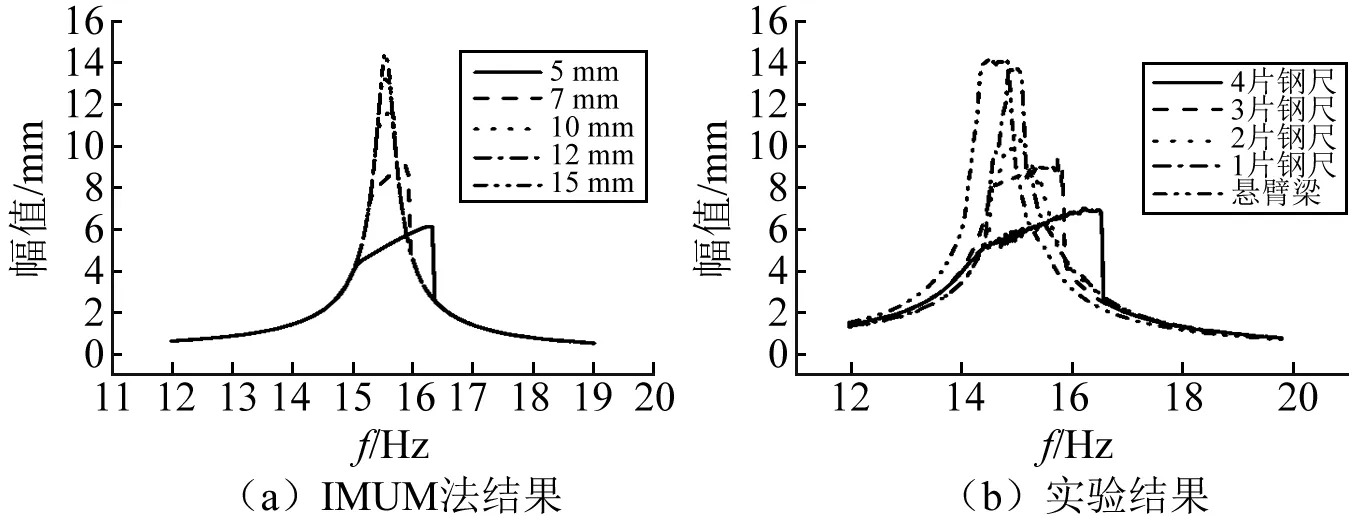
3.2 仿真计算与实验结果的对比

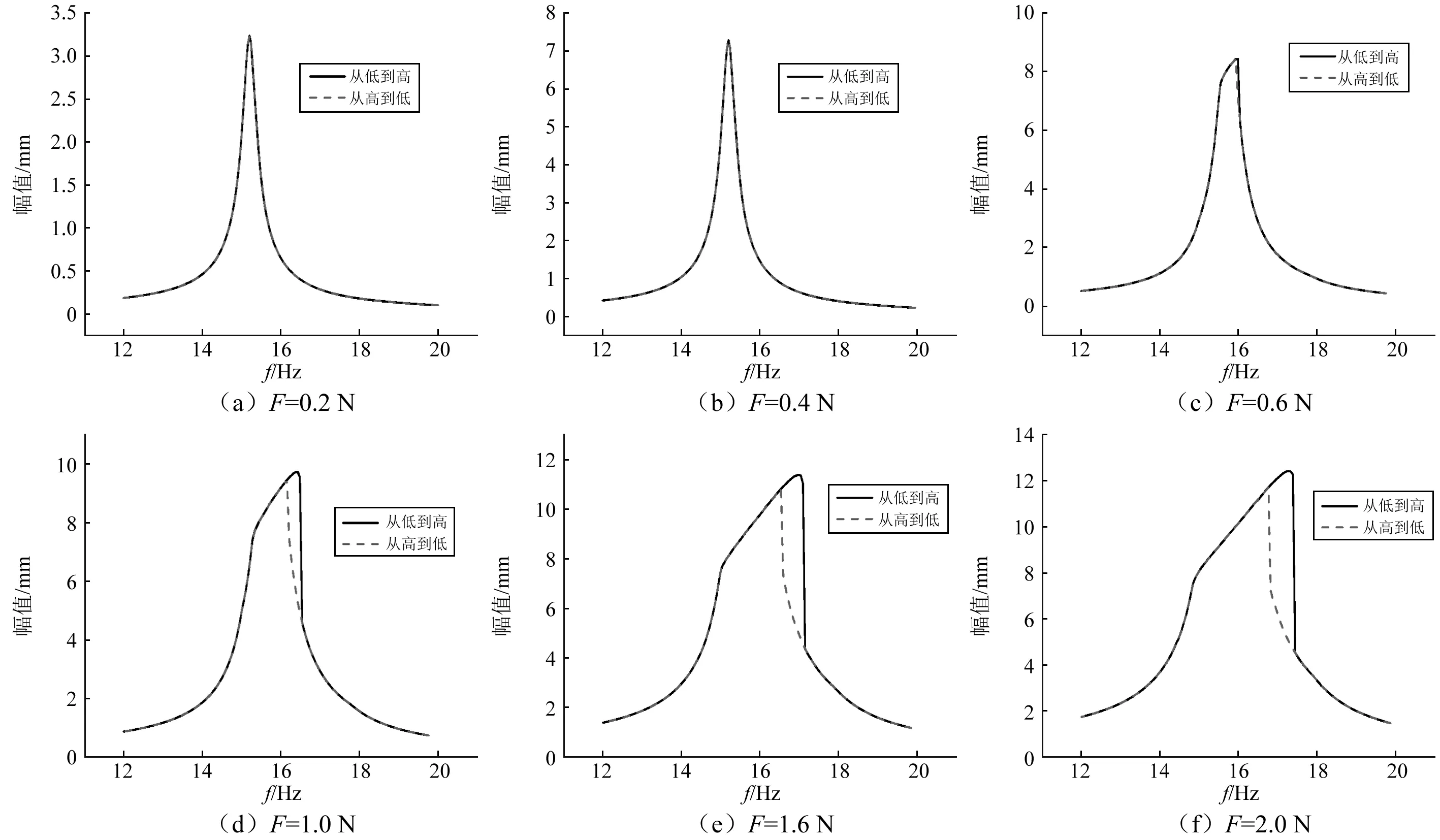
4 结 论

