基于BP神经网络的穿浪双体船姿态自适应PID控制∗

梁星宇 赵 萌 宋立忠

（海军工程大学电气工程学院 武汉 430033）

1 引言

随着海战场环境的日益复杂，如何提高舰船耐波性能从而增强恶劣海情下的作战效能已成为军事方向的重要课题。穿浪双体船航速高，载运方式灵活，承载量大，耐波性能优良，能够在一般高速船无法航行的海况中正常执行任务，因此受各国海军青睐，被广泛用于近海作战和突击兵力运输［1］。但是，由于海洋环境影响，穿浪双体船在高速航行过程中产生的垂荡和纵摇不仅导致船员产生严重不适，还会使舰船失速和损坏主要部件，严重影响其安全性能。针对此问题，人们通常在艏部增加可控的T型水翼以构造姿态控制系统，通过控制其提供的恢复力和力矩来抑制舰船的纵向运动。实际情况表明，利用该系统，可以有效减小纵摇和垂荡运动，提高舰船的安全性、稳定性和舒适性。常规的研究往往利用PID控制进行设计，但在复杂、易变的外界条件下，其参数获取难度较大，且很难实现最佳抑制效果。以BP神经网络为例的现代智能算法常和PID结合用以面向实际控制。BP神经网络所具有的非线性表达能力，可以通过对系统性能的学习来实现最佳组合的PID控制。本文给出了穿浪双体船的纵向运动模型，并从控制的角度，基于BP神经网络设计了自适应PID控制器，并对穿浪双体船的纵向和垂荡运动进行仿真实验。仿真结果表明，该控制器能够有效抑制舰船的纵向运动，改善舰船的性能。

2 模型分析

2.1 穿浪双体船纵向运动控制模型

由于穿浪双体船的两个船体关于纵向中截面对称，故其横向运动和纵向运动无耦合。T型水翼利用翼面产生的恢复力和力矩用来抵消波浪的力和力矩，从而减小垂荡和纵摇的幅度。假设穿浪双体船以稳定航向和定常速度在无限深水域航行，水下部分的片体足够细长，波浪扰动引起的船体运动微辐，不考虑风和流对运动的影响。根据文献［2］，可确定在海浪扰动作用下，艏部设置T型水翼的舰船纵向关于垂荡和纵摇耦合运动的数学模型。其方程组如下：

式中，M为舰船的质量；Aik为水的附加质量；Bik为水动力阻尼系数；Cik为恢复力系数；下角标3和5分别为垂荡和纵摇的相关参数，η、η̇、η̈分别为位移、速度、加速度；I5为纵摇惯性力矩，Fw和Mw为海浪引起的垂荡扰动力和纵摇扰动力矩；FT和MT分别为T型水翼提供的纵向升力和力矩。Aik、Bik、Cik可利用2.5D理论［3］进行水动力学计算，在此不再给出具体求解公式。

因此，其状态空间模型可表示为

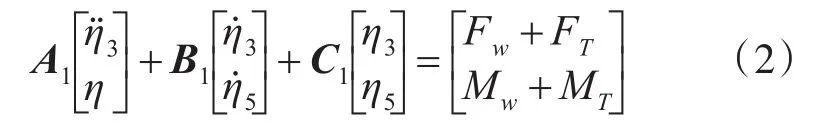
式中，

2.2 T型水翼模型

当穿浪双体船航行过程中发生摇晃时，水流会以某一攻角流向T型水翼的表面，在翼面上会产生与其运动方向相反的力和力矩，从而阻碍舰船的纵向运动。基于文献［4］，计算公式如下：

式中，ρ为水的密度；A为T型水翼的表面积；U为船速（kn）；α为翼面的有效攻角（°），有效范围为为水翼的升力系数，利用Fluent软件可以仿真T型水翼在不同来流速度下的升力系数。在α很小的情况下可视为常量。da是舰船重心到T型水翼安装处稳定力作用中心的距离。

2.3 随机海浪扰动力模型

考虑海浪干扰时，常采用余弦序列权重系数法来计算波浪作用于船体的随机干扰力和力矩［5］。

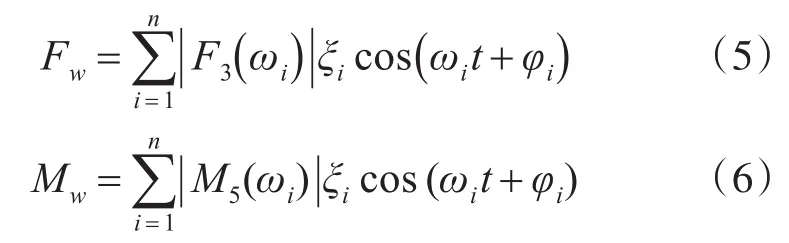
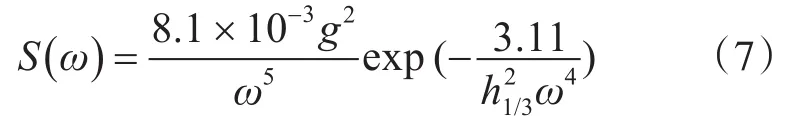
式中，g为重力加速度，h1/3为海浪的有义波高，可根据ITTC推荐值确定。

3 基于BP神经网络的自适应控制器设计

3.1 常规PID控制

传统的PID控制器模型如下：

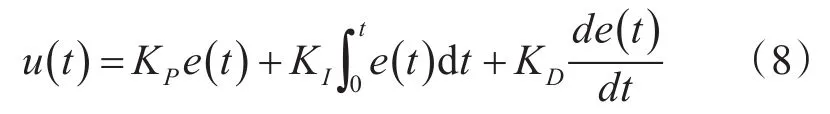
式中：u(t)为控制量，这里指穿浪双体船的T型水翼攻角，e(t)为期望输出与实际输出之间的偏差信号。KP、KI、KD分别为比例、积分、微分系数。

穿浪双体船姿态控制系统实际是一个SIMO系统（Single-Input Multiple-Output），因此应该分别针对垂荡和纵摇两个通道进行PID控制器设计［6］。

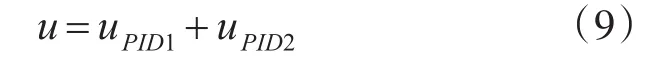
3.2 基于BP神经网络的自适应PID控制

穿浪双体船的纵向运动具有显著的非线性和时变性，各类不确定的干扰会影响控制效果，PID控制的控制品质难以保证。同时，由于系统参数整定方法复杂，PID控制器参数往往不良，对环境的适应力较差。为了克服传统PID控制的缺陷，可考虑将BP神经网络与PID控制结合起来。多层前馈网络的反馈传播学习算法（BP算法）是神经网络模型中使用最广泛的一类，它是梯度下降法在多层前馈网络中的应用。BP神经网络所具有的非线性表达能力，可以通过对系统性能的学习，建立参数自适应的PID控制器，从而实现最佳组合的PID控制。

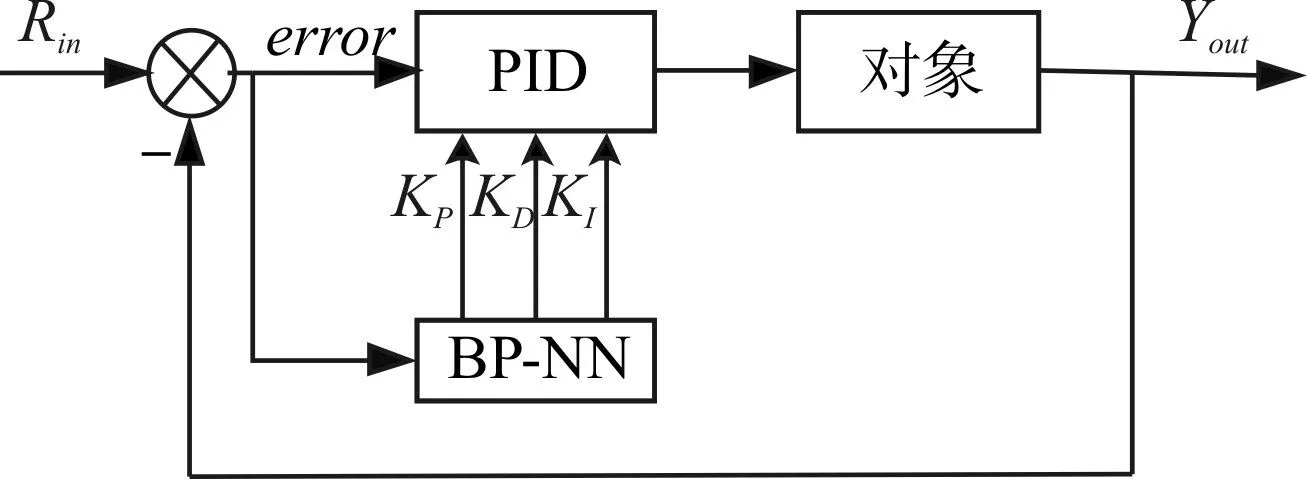
图1 基于BP神经网络的自适应PID控制原理

BP算法的学习过程由正向传播和反向传播组成。在正向传播过程中，输入信息从输入层经隐层逐层处理，并传向输出层，每层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转至反向传播过程，即按各层各神经元状态对整个感知器输出的影响，将该误差信号按原来正向传播的路径分解反向计算，据此调整各层神经元的权值，使误差信号减小。

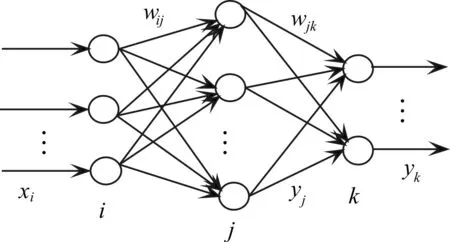
图2 单隐层BP神经网络示意图

设各单隐层BP网络的各节点的输入为x，输出为y，输入节点与隐含节点的网络权值为wij，隐含节点与输出节点间的网络权值为wjk，输出节点的期望输出为dk，学习速率为η，惯性系数为α，则BP模型的计算公式如下：

1）前向传播：计算网络的输出。

2）定义网络误差函数。

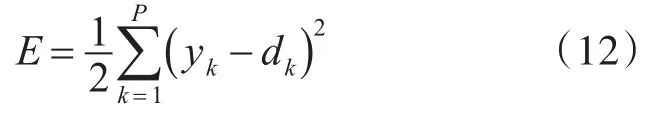
3）反向传播：调整各层间的权值。

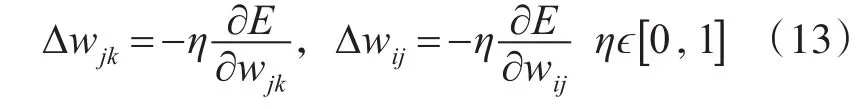
4）带惯性系数α的在线学习。

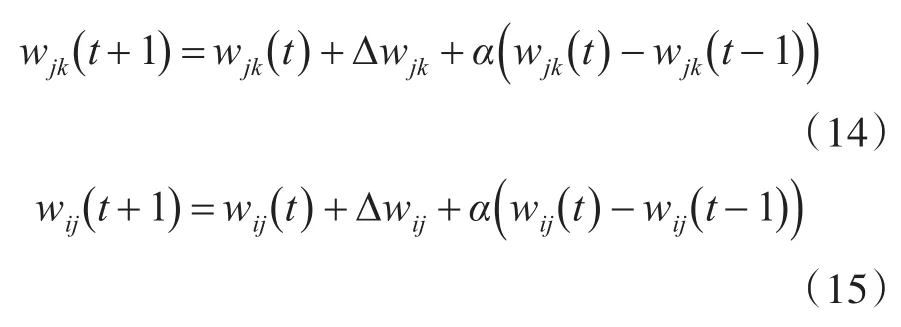
穿浪双体船的自适应PID控制器是在传统PID控制基础上通过参数在线调整，从而增强控制器的鲁棒性和自适应性。因此，控制器基本框架设计与常规PID控制器相同。

三层及三层以上BP网络可以任意精度逼近任意非线性函数。增加层数虽然可以更进一步降低误差，提高精度，但同时也使网络复杂化，从而增加网络权值的训练时间。网络训练精度的提高，可以通过采用一个隐含层而增加神经元数量的方法来获得。因此，可将BP神经网络设计为单隐层四输入四输出结构：

输入：-η3、 - η̇3、 - η5、 - η̇5

输出：KP1、KD1、KP2、KD2

激活函数：

输入层和隐层的激活函数取Sigmoid函数，即：

因为PID控制器的参数非负，所以在输出层选取非负的Sigmoid函数，即：

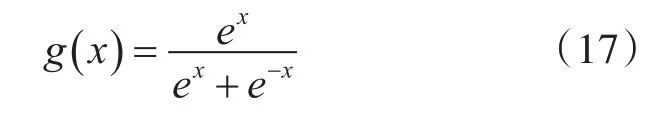
4 仿真研究

根据一艘船长L=90m，排水量D=737.348t，吃水T=2.6m的穿浪双体船进行研究，此时航速40 kn。根据计算切片理论计算［7］，其相应的状态空间系数如下：

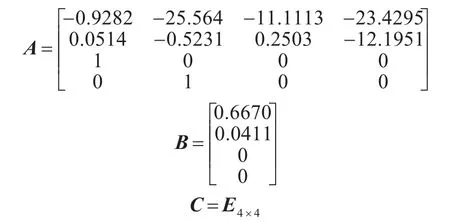
在随机海浪有义波高2.5m的情况下，我们对传统PID控制器和自适应PID控制器分别进行仿真，仿真得到的控制效果如图3和图4所示。图3是参数已经充分调试和优化的PID控制器的仿真结果。图4是基于BP神经网络的自适应PID控制器的仿真结果。

图3 PID控制仿真结果

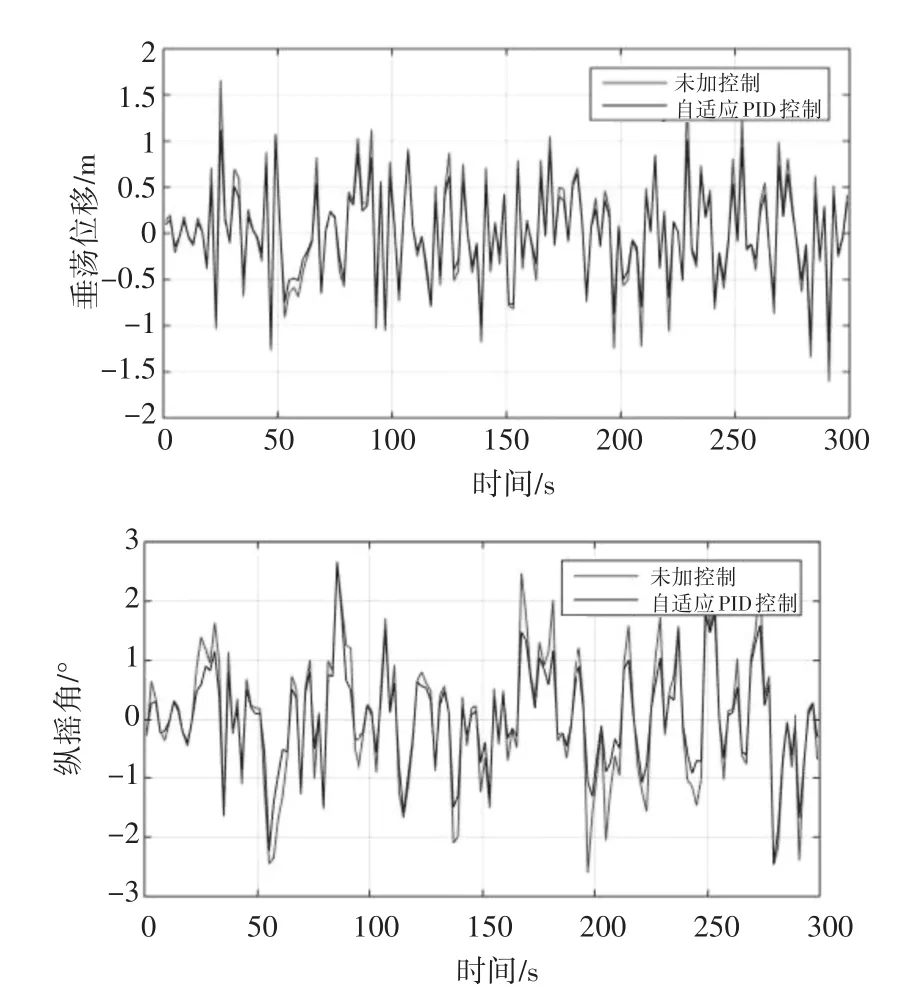
图4 基于BP神经网络的自适应控制仿真结果

由图所示，利用传统PID控制器，穿浪双体船的垂荡减摇达到16%，纵摇减摇达到47%；利用基于BP神经网络的自适应PID控制器，垂荡减摇达到24%，纵摇减摇达到62%。相对于传统PID控制，效果更好。

5 结语

通过利用BP神经网络，在线整定PID控制参数，建立参数自适应的PID控制器，可以克服传统PID控制的缺陷，并有效提高控制效果，从而解决自动控制参数整定问题。本方法对于穿浪双体船纵向运动控制为例的系统，具有实际应用价值。应用中通过对神经网络结构、学习速率和惯性系数做进一步优化，有望取得更好的控制效果。