群体智能算法在机器学习当中的应用

詹煜 吴冠辰

摘 要 大多数机器学习都是使用梯度下降法来对损失函数进行优化的。但梯度下降也要求损失函数必须是凸函数，对于损失函数为非凸函数的情形优化能力有限。群体智能算法是对非凸函数的优化有较好的效果。文章尝试与群体智能算法代替梯度下降，来对凸损失函数进行优化，并在常见的数据集上取得了与梯度下降相似的效果。

关键词 机器学习；优化；梯度下降；群体智能算法

中图分类号 TP2 文献标识码 A 文章编号 1674-6708（2018）218-0115-02

随着信息技术的普及，越来越多的领域发挥着重要的效果，大多数的机器学习算法都是通过对某个参数进行优化，以使损失函数最小或最大化，目前机器学习领域常用的优化算法有梯度下降法[ 1 ]，共轭梯度法，Momentum算法[ 2 ]及其变体adam等，目前应用最多的是梯度下降法，但以上优化算法，针对的损失函数都是凸函数，而群体智能算法，可以很好地应对非凸函数的优化，因此本文试图用群体智能算法代替梯度下降，对损失函数进行优化，以便未来适应于凸或非凸损失函数的优化问题。本文第一节简要介绍凸函数与梯度下降，第二节简要介绍了群体智能算法，第三节设计实验，并分析实验结果。

梯度下降是迭代法的一种，其计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。在损失函数是凸函数的情况下，梯度下降能收敛到全局最小值。但是应用于非凸函数时，梯度下降很容易陷入局部最小值，而无法获得全局最小值。梯度下降应用于凸函数的示例如图1所示。梯度下降应用于非凸函数的示例如图2所示。

图1中凸函数所标识的点（Global？minimum），是通过梯度下降能获得的全局最小值。同时，可以看到函数上两点的连线（图中虚线所示）会处在图像的下方，因此图1也是一个典型的凸函数的图像。

从图2中可以看出，非凸函数会存在局部最小值（Local？minimum），梯度下降法会有陷于局部最小值的可能而无法获取全局最小值。同时，可以看到函数上两点的连线（图中虚线所示）会处在图像的下方，因此图2也是一个典型的非凸函数的图像。

2 群体智能算法

群体智能算法[4]的算法起源于人类对自然界群居生物（如鱼群、蚂蚁、蜜蜂、狮群等）的观察和研究，分析这些生物群体所表现出来的智能模式，并将这些智能模式抽象为算法。群体只能算法的表现是需要相当是数量的种群“个体”，来实现对某个问题的求解需要。由于“群体”具有分布式、自组织、协作性等特点，因此群体智能算法的鲁棒性较好，实现也比較简单，常被用于优化领域。常见的群体算法有蚁群算法、人工鱼群算法、人工蜂群算法、粒子群算法等。

3 实验设计及结果分析

由于群体智能算法常被用于优化领域，因此本文考虑将群体智能算法代替梯度下降，对机器学习的损失函数进行优化。由于群体智能算法较多，本文选取人工鱼群算法来进行相应的对比。

人工鱼群算法[ 5 ]是李晓磊等人提出，该算法模拟鱼群的觅食聚集行为实现寻找全局最优。该算法中给鱼群定义了的三大基本行动方式：即觅食、聚群和追尾。通过鱼群中各个体的局部寻优，通过追尾和聚群行为，最终获得全局最优值。人工鱼群算法的实现步骤为：

1）全局初始化：？包括种群规模、个体的初始位置、个体的搜索范围（视野），个体的移动步长、子集拥挤程度、迭代次数（即终止条件）；

2）计算个体的适应值，将最优个体的状态进行公告；

3）对每个个体进行评价，根据评价，确认个体下一步的行动，包括觅食、聚群、追尾和随机行为；

4）执行个体行动，并在行动后更新个性的相应指标，并生成新鱼群；

5）评价所有个体。若某个个体状态优于公告状态，则将该个体的状态更新为公告状态；

6）当公告状态达到最优解或满足相应误差精度或算法达到迭代次数上限时算法结束，否则转步骤3。

试验采用机器学习中常用的Iris数据集进行测试，实验目的是将人工鱼群算法与SGD（随机梯度下降）在分类及回归任务上进行对比。评价指标是准确率，在SGD算法中根据采用数据集的不同；训练集、验证集、测试集的随机划分；是否采用交叉验证；超参数设定的不同等方面的因素，在试验中会产生不同结果。而在人工鱼群算法中，根据种群数量、迭代次数等设定的不同，也会对实验结果有所影响。实验中的人工鱼群算法设定种群数量为60，迭代次数上限为500次。实验结果如表1所示。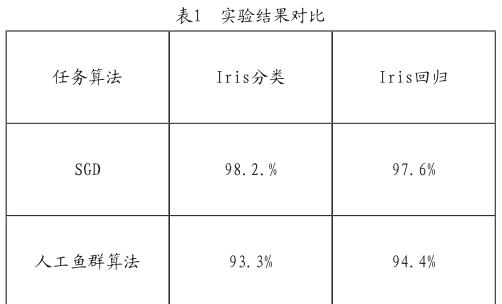

从实验结果中看，群体智能算法在机器学习中的性能相比SGD还是有一定的欠缺，但是其差距也在可接受的范围内（≤5%）。但是群体智能算法可以应对于损失函数是非凸函数的情形，因此将群体智能算法应用于非凸损失函数中是下一步的研究方向。

参考文献

[1]陈振宏，兰艳艳，郭嘉丰，等.基于差异合并的分布式随机梯度下降算法[J].计算机学报，2015，38（10）：2054-2063.

[2]欧世峰，高颖，赵晓晖.基于随机梯度的变动量因子自适应白化算法[J].自动化学报，2012，38（8）：1370-1374.

[3]Stephen Boyd.Convex Optimization[M].北京：清华大学出版社，2013，61-167.

[4]余建平，周新民，陈明.群体智能典型算法研究综述[J].计算机工程与应用，2010，46（25）：1-4，74.

[5]马宪民，刘妮.自适应视野的人工鱼群算法求解最短路径问题[J].通信学报，2014，35（1）：1-6.