应对并补电网下DFIG系统高频谐振的宽频阻抗重塑策略

年 珩, 庞 博, 许国东, 邱纪星

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 浙江运达风电股份有限公司, 浙江省杭州市 310012)

0 引言

随着风力发电技术的快速发展,基于双馈式感应发电机(DFIG)的风力发电系统在新能源发电领域的比例越来越高[1-5]。风力发电系统并网运行一般认为电网为无穷大系统,实际中当电网表现为阻抗不能忽略的弱电网时,并网风电系统易进入不稳定运行状态[1-9]。根据阻抗稳定性理论[2],并网系统运行稳定性取决于其输出阻抗和电网阻抗在幅值交点位置的相位裕度。如果此时相位裕度不足,并网点电压就会产生谐波谐振,恶化电网稳定性及风电系统运行性能,甚至导致脱网[2-5]。

弱电网下DFIG系统并网运行产生的谐波谐振,可以分为次同步振荡(SSR)和高频振荡(HFR)。其中SSR主要出现在串补电网中[6-7,10-13]。并联补偿电网可以提高系统功率因数,改善系统电压质量,并且降低线路损耗,其特性表现为频率增大时,阻抗呈现出明显的容性特征。并联补偿的方式可以采用固定电容器补偿，也可以采用并联无功发生器,前者接入实际的电容,后者根据无功补偿容量可以等效为电容并联在电网中[11]。DFIG系统由于电机绕组和网侧变流器(GSC)滤波电抗的存在,高频段主要表现为感性特征,此时DFIG系统和电网阻抗相位十分接近180°,一旦在该频段范围内DFIG系统与电网阻抗产生幅值交点,即会产生频率范围高于基频的HFR[11,14-18],导致并网点电压出现持续的高频谐波振荡,恶化风机并网运行性能。

双馈风电系统包括网侧变流器和机侧变流器,这两种变流器均会导致并网双馈风机出现高频振荡现象。对于网侧变流器,文献[8-9]中针对LCL型并网逆变器接入交流网系统发生频率高于基频(谐振频率为500～1 000 Hz)的谐振现象进行了分析,对于机侧变流器;文献[11,19-20]分析了双馈系统接入交流电网时产生的频率高于基频的谐振现象(谐振频率为500～2 000 Hz),针对风电接入实际的一般弱电网(RL阻抗),串联补偿弱电网,并联补偿弱电网下可能发生的谐振现象进行了分析,指出由于双馈风电系统在高频下阻抗为感性,因此在并联补偿电网下,双馈风电系统会产生频率高于基频的振荡现象;文献[20]指出采用电缆输电的海上风电中由于电网阻抗存在多个等效电容,也会发生HFR现象。

为分析弱电网下DFIG系统并网运行产生的HFR问题,必须对DFIG系统和弱电网的阻抗进行建模。DFIG系统变流器由网侧变流器和转子侧变流器(RSC)组成,DFIG系统阻抗可表示为GSC和DFIG定子绕组侧的并联[11-14]。DFIG系统发生HFR的频率一般在几百到几千赫兹[14],其中变流器锁相环由于带宽较低(一般小于100 Hz),因此对系统高频阻抗特性影响很小,建模时可以忽略[11-14]。在新能源并网系统的阻抗建模研究中,文献[16]对并网逆变器进行了阻抗建模,并分析了电网阻抗变化导致的并网逆变器稳定性问题。文献[17]建立了基于LCL滤波的并网逆变器阻抗模型,提出了基于虚拟阻抗的谐振抑制方法,提升了并网逆变器对弱电网的适应能力。文献[18]通过建立DFIG阻抗模型,提出了基于虚拟阻抗的DFIG系统谐振抑制方法。

针对并联补偿电网下DFIG系统出现的HFR问题,文献[19-20]建立了DFIG及并联补偿电网高频阻抗模型,并基于阻抗稳定性理论分析了并联补偿电网以及多重并联补偿电网下的HFR现象,提出了基于谐振频率检测的HFR抑制策略。

目前已有的DFIG系统HFR抑制策略均需准确检测谐振频率,通过在谐振频率点引入虚拟阻抗实现HFR抑制。这种基于谐振频率检测的HFR抑制策略存在如下问题。

1)谐振频率检测方法一般采用傅里叶算法、小波分析法、自适应窗函数法等[21-23],存在算法复杂、计算量大的缺点。

2)电网并补度变化时将导致HFR频率点偏移,目前基于自适应陷波器锁频环的谐振频率检测方法无法快速动态跟随谐振频率变化[22,24],因此在HFR频率变化的动态过程中,锁频环节性能下降[25],导致HFR抑制策略失效。

3)在谐振频率点引入的虚拟阻抗会影响系统阻抗并使得谐振频率点出现偏移,从而影响系统HFR的抑制能力,甚至会出现谐振点在两个频率之间变化的Whack-Mole现象[26]。

基于以上分析,本文提出并补电网下基于阻抗重塑的DFIG系统高频谐振抑制策略,使得DFIG系统阻抗在高频范围内具有足够的相位裕度,从而无需谐振频率检测环节并实现对HFR的抑制,提升了DFIG系统对于并补电网的适应能力,并通过PSCAD/EMTDC建模验证控制策略的有效性。

1 DFIG及弱电网阻抗模型及稳定性分析

DFIG系统中GSC通过网侧滤波环节接入电网,用于保持直流母线稳定,RSC用于实现发电机输出功率的控制,其中GSC与RSC通过直流母线相连。DFIG系统的阻抗建模及其分析工作已经有了相关的研究[10-20],这里针对DFIG系统的阻抗模型进行简要介绍。

1.1 双馈风机阻抗模型

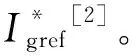
Zgsc=Hgi(s-jω0)Hd(s-jω0)

(1)

式中:Hgi(s-jω0)为GSC电流控制器传递函数,Hgi(s)为电流环比例—积分(PI)控制器;Hd(s-jω0)为控制环节及调制导致的数字延时,Hd(s)=e-sT,其中T≈1.5T0,T0为采样周期[16-20]。由于电流控制器建立在同步旋转dq坐标系下,因此在静止坐标下传递函数存在基频ω0偏移。

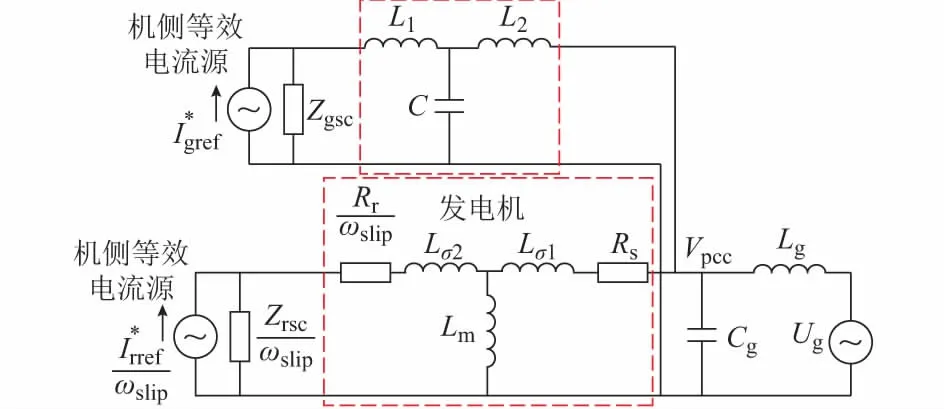
图1 GSC及发电机侧等效电路图Fig.1 Equivalent circuit of GSC and generator

根据图1,考虑LCL滤波器的后GSC的输出阻抗可以表示为:

(2)

式中:L1,L2,C分别为LCL滤波器的滤波电感和电容。

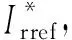
Zrsc=Hri(s-jω0)Hd(s-jω0)

(3)

式中:Hri(s)为RSC电流控制器传递函数。但由于Zrsc串联在转子绕组上,因此经过绕组折算后[19-20]的RSC阻抗为

(4)

式中:ωslip为滑差角频率。

DFIG定子侧的输出阻抗可表述为:

(5)

式中:Rr′=Rr/ωslip为等效到定子侧的转子电阻,其中Rr为转子电阻;Rs为定子电阻;Lσ1和Lσ2分别为定、转子漏感;Lm为励磁电感。

DFIG系统阻抗可以表述为式(2)和式(5)两部分的并联,即

(6)

1.2 并联补偿电网阻抗模型

如果DFIG系统并入的电网为理想的无穷大电网,可采用理想电压源作为等效[1-4],而实际中电网线路阻抗无法忽略,此时电网可等效为带阻抗的电压源。对于并联补偿电网,此时电网中存在容性的阻抗环节,通常可以采用一个并联电容作为等效[11,19-20]。

如果考虑风机并网点的升压变压器,那么电网阻抗则需要考虑变压器匝比[19-20],并联补偿弱电网阻抗可以等效为:

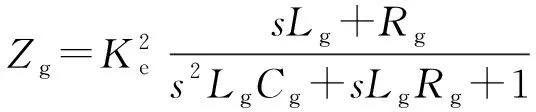
(7)

式中:Ke为变压器匝比;Lg,Rg,Cg分别为电网等效电感、电阻及并联补偿等效电容。

1.3 并补电网下DFIG系统HFR分析

根据式(6)和式(7)可以分析DFIG系统及并补电网的阻抗特性,进而研究并联补偿产生的HFR问题。附录A表A1给出了本文分析所采用的DFIG系统参数及并联补偿电网参数。

附录A图A1中给出了DFIG系统的GSC及RSC侧输出阻抗及整个系统的输出阻抗,由于DFIG系统HFR频率范围一般为几百到几千赫兹,因此这里给出200 Hz以上并联电容为7.5,3.75,1.5 μF的电网阻抗曲线。可以看出,并联补偿电网的阻抗曲线在频率较低时处为感性,高频处表现为容性,相位骤变的频率点则取决于并联补偿度的大小。DFIG系统阻抗曲线在大部分频率范围都表现出感性,而在1 300～3 500 Hz之间表现出容性,根据DFIG系统阻抗模型(式(6)),这是由DFIG系统中GSC侧LCL滤波电容所导致的。同时DFIG系统输出阻抗在920～1 500 Hz时,定子侧阻抗会对输出阻抗产生明显影响,此时阻抗由两侧共同决定。在此频率段之外,网侧变流器阻抗对输出阻抗能起到主导作用。

这里以并联补偿电容为7.5 μF(系统并联补偿度为11.9%)时的DFIG阻抗曲线为例,分析DFIG与并联补偿电网相互作用产生的HFR问题。从附录A图A1中可以看出,此时电网阻抗与DFIG阻抗曲线在频率f1(524 Hz)和f2(535 Hz)有2个交点。其中f1处DFIG系统和电网阻抗相位均为接近90°,而f2处两者阻抗相位相位差约为178°,此时f2处存在HFR问题。

附录A图A1中也给出了并联补偿电容为7.5,3.75,1.5 μF时的电网阻抗曲线。可以看出,并联补偿度越低,即并联电容越大,谐振频率越低。同时,DFIG定子侧的阻抗大于GSC侧的阻抗,在200 Hz以上的大部分频率范围,DFIG系统阻抗与GSC侧阻抗基本重合。因此,DFIG系统输出阻抗主要取决于GSC侧阻抗,故本文的HFR抑制策略将在GSC侧加入。

从附录A图A1中还可以看出,电网阻抗与DFIG系统阻抗会有两个幅值交点,电网阻抗在频率较小的交点f1处会表现出接近90°的相位,而在频率较高点f2处则变现为-90°的相位。如果电网阻抗与DFIG系统阻抗相位差接近180°,那么系统将会产生谐波谐振,即频率点f2会出现谐振。因此,为了消除DFIG系统并网后的HFR,必须对DFIG系统在频率f2处阻抗的相位进行修正,使得DFIG接入并补电网后具有足够的相位裕度,同时也要确保f1处不会因为阻抗重塑而产生相位裕度不够。

2 基于阻抗重塑的DFIG系统HFR抑制策略

为了提升DFIG对不同并补电网下HFR的抑制能力,进一步增强DFIG系统对弱电网的主动适应性,本文提出DFIG系统高频范围内阻抗的重塑方法,以适应不同并联补偿电网的并网运行条件。本文提出的HFR抑制策略不需要谐振频率的检测环节,因此在谐振频率变化的暂态过程中控制性能不受影响,同时能够避免HFR抑制中产生的谐振频率偏移现象[26],从而使DFIG对不同并联补偿度电网具有更强的适应性。

2.1 目前HFR抑制策略的问题

目前已有的HFR抑制策略滤波环节采用的多为谐振控制器,以改变谐振点或者谐振点附近频率段的阻抗[11,14]。谐振频率发生变化时,谐振检测环节动态性能不佳,控制器难以保持良好的控制能力。

附录A图A2给出了目前已有HFR抑制策略[19-20]下DFIG系统输出电流波形,此时并联补偿电容为7.5 μF。从图中可以看出,6 s之前HFR抑制策略未使能时,DFIG系统在535 Hz处产生HFR,与附录A图A1分析相一致,此时谐波电压和电流含量分别为24.07%和15.5%。6 s时加入基于谐振频率检测的HFR抑制策略,系统谐波电压和电流分别下降为6.01%和2.82%,表明已有HFR抑制策略可有效抑制并补电网下的谐振问题。在6.06 s时,电网并联补偿电容从7.5 μF变为3.75 μF,此时系统谐振频率变为715 Hz,由于谐振频率检测环节难以快速跟踪谐振频率点的变化,导致DFIG系统在715 Hz处的谐波电压和电流含量分别为15.06%和7.6%。可以看到,目前基于频率检测的HFR抑制策略难以应对并补度改变导致的谐振频率变化。

2.2 基于阻抗重塑的HFR抑制策略

为了避免对谐振频率进行实时检测,本文通过在GSC中进行阻抗重塑以改变DFIG系统高频段阻抗的相位特性,提高DFIG系统在不同并补电网下的适应能力,所提控制策略如图2所示。图中:SVM为空间矢量脉宽调制。其中RSC采用转子电流作为控制目标,用于实现最大功率追踪控制,而GSC电流控制中分成基频控制和高频控制两个控制闭环,其中基频控制用于实现直流电压稳定和交流侧无功功率控制;高频控制环通过阻抗重塑控制器对GSC交流侧电流高频分量进行调节,用于修正高频范围内GSC阻抗的相位。

图2 并补电网下DFIG高频谐振抑制策略Fig.2 HFR damping control strategy of DFIG system on parallel compensated grid

根据图2,GSC和RSC参考电压可表示为:

(8)

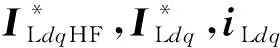
(9)

因此,通过基频控制环和高频控制环的独立控制,保证DFIG系统并网发电不受影响的情况下,具有HFR的抑制能力,下一节将进一步分析阻抗重塑控制器的设计方法及其对基频控制的影响。

2.3 阻抗重塑器实现方式

文献[27]中总结了目前常用的变流器阻抗重塑方法,包括电流反馈闭环及电容电压反馈闭环等方式。文献[27]指出电流反馈和电压反馈均可以对变流器系统进行阻抗重塑。两者原理上都可以实现相同阻抗引入。本文中的电机控制系统本身有指令电流控制环,采用电流反馈不需要增加电流传感器。因此，这里采用构造电流反馈闭环的方式进行阻抗重塑。

根据1.3节中的分析,由于高频段对GSC侧阻抗进行重塑有更好的阻抗重塑的效果,因此本文所提HFR抑制策略考虑在GSC侧实现。根据图1中等效电路及图2控制框图,GSC控制回路传递函数如图3(a)所示。

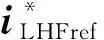
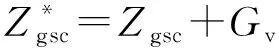
(10)

阻抗重塑控制器用于改变GSC输出阻抗在出现HFR频率段的相位特性,由两部分组成：一部分是滤波环节,用于滤出L1上的高频电流分量,可表示为Gfilter;另一部分用于对L1上的高频电流分量进行相位补偿。本文阻抗重塑控制器的滤波环节采用积分(Ⅰ)型切比雪夫高通滤波器(阶数为五阶;纹波系数为0.1;截止频率ωn=50 Hz),其传递函数可表示为[28]:

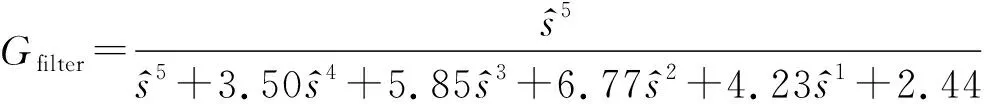
(11)

图3 基于阻抗重塑的GSC框图和DFIG系统阻抗特性Fig.3 Block diagram of GSC based on impedance shaping and impedance characteristic of DFIG system

相位补偿环节采用负感性阻抗,可表示为:

Zv=-jωLv=|Zv|∠θv

(12)

式中:|Zv|为相位补偿环节的幅值,用于表明阻抗重塑器修正阻抗的程度;θv为相位补偿环节的相位,用来对GSC在高频段阻抗的相位进行修正。

由附录A图A1可见,产生HFR处的DFIG系统阻抗多为接近90°,因此θv选取-90°以最大程度地提高阻抗重塑器的相位补偿能力。

因此,阻抗重塑器的传递函数可表示为:

Gv=GfilterZv

(13)

为了实现GSC输出阻抗在出现HFR频率段的相位特性修正,理想的阻抗重塑控制器应具有以下特征:①基频附近几乎无增益,从而避免对基频控制的影响;②由于DFIG阻抗随频率上升而增大,因此阻抗重塑控制器增益也应随着频率上升而增大;③根据1.3节中的分析,重塑后GSC交流侧阻抗相位为-90°～90°。理想的阻抗重塑器的频率特性参见附录A图A2。

附录A图A2为理想的阻抗重塑器特性和基于切比雪夫滤波器阻抗重塑器特性对比,可以看到基于切比雪夫滤波器阻抗重塑器能够在低频段保持很低增益,而在高频率段阻抗重塑器增益能够随着频率上升而增大,从附录A图A2中可以看到:100 Hz和10 Hz之间的增益差达到了95 dB,这说明实际阻抗重塑器能够确保低频处具有很低的增益。同时本文所采用的阻抗重塑控制器能够在100～5 000 Hz频率范围相位均保持在-90°～90°之间,因此本文采用的阻抗重塑器能有效地对DFIG系统阻抗进行相位补偿,确保并补电网下DFIG与电网的互联系统在高频段不会因为相位裕度不足而产生HFR。

图3(b)中给出了阻抗重塑后DFIG系统阻抗曲线以及并补电容为3.75 μF时的电网阻抗曲线。可以看到,此时电网和阻抗重塑前的DFIG有两个幅值交点,其中P1(726 Hz)处电网和DFIG阻抗相位差为172°,此时系统会发生高频谐振。而阻抗重塑后DFIG系统和电网阻抗的幅值交点偏移至P2(655 Hz)和P3(765 Hz),其中P2和P3处DFIG系统与电网阻抗相位差分别为42°和130°,从而避免了可能出现的HFR问题。同时可以看到,在200～5 000 Hz之间,重塑后的DFIG系统阻抗相位始终保持在-30°～48°之间,这就保证了对于并联补偿参数变化的弱电网,DFIG与电网的互联系统都至少有42°的相位裕度。因此,本文提出的阻抗重塑策略无须检测谐振频率,能够有效抑制并联补偿度变化导致的谐振频率点偏移现象,从而提升DFIG系统应对并补电网的适应能力。

2.4 阻抗重塑控制器对基频控制的影响

阻抗重塑控制器的加入可能会对基频控制产生稳态或者动态影响,因此这里有必要分析阻抗重塑控制器的引入对基频控制产生的影响。

式(14)给出了系统相位裕度的计算表达式:

(14)

式中:s1(=jω1)和s2分别为与DFIG和电网阻抗幅值相等的频率点;θm为系统相位裕度。

根据式(14)可以得到在不同延时参数下DFIG重塑后的系统相位裕度,如图4(a)所示。图中:|Zv|=10-4K。可以看出,随着延时的增大,系统相位裕度逐渐下降,实际中DFIG系统的采样频率一般为1～10 kHz,此时对应图中延时为k=3～4(k=-lgTs,其中Ts为采样周期),此时相位裕度仍能保证不低于20°,以Ts=0.000 2为例,此时系统在不同并联补偿度下相位裕度为22°～28°,此方法提升DFIG的系统相位裕度是有效的。

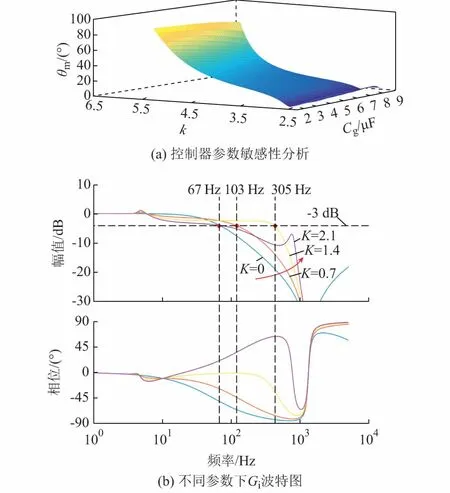
图4 控制器参数敏感性分析及动态特性分析Fig.4 Sensitivity analysis of controller parameters and analysis of dynamic performance

由于控制器加入在GSC侧,因此对于GSC侧控制,根据图3(a)及式(8)可以得到:

(15)

式中:ig为网侧电流;Vpcc为公共耦合点电压。

GSC交流侧阻抗重塑会导致基频控制性能发生改变,如式(16)和式(17)所示,阻抗重塑前后基频电流控制闭环传递函数可以表述为:

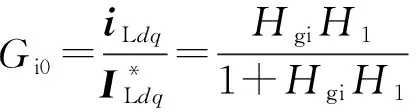
(16)

(17)

式中:Gi0和Gi分别为Gv引入前后的基频电流控制闭环传递函数;Δ=1+(Gv+Hgi)H1。H1只与LCL滤波环节有关,其表达式为

(18)

式中:ZL1,ZL2,ZC分别为L1,L2,C的阻抗。

在dq坐标系下,基频即s=jω|ω→0,根据式(16)至式(18)可得:

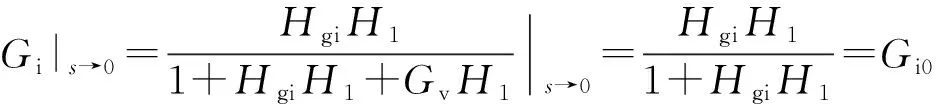
(19)

可以看出,所加入的阻抗重塑控制器不会对基频电流控制造成影响,从而保证了阻抗重塑不会影响原有矢量控制性能。

图4(b)给出了阻抗重塑控制器不同参数下Gi波特图。可以看到,不同阻抗重塑控制器参数下在接近零频时增益均为0 dB,相位均为0°,表明阻抗重塑控制器不会影响基频电流控制精度。同时,随着K的增大,截止频率随之增大,控制带宽有所增加,当|Zv|大于2.1×10-4时,控制带宽反而会随着K增大有所降低。

3 仿真验证

为验证所提出的并补电网下DFIG系统高频谐振抑制策略,本文在PSCAD/EMTDC下建立仿真模型,DFIG系统及电网参数参见附录A表A1。

图5(a)给出了当电网投入不同并联补偿电容时,DFIG系统并网点的电压和电流波形,其中区间0为未投入并联补偿电容时DFIG系统的运行波形,区间1至5分别为并补电容为7.5,4.5,3.75,2.7,2 μF情况下DFIG系统的运行波形。可以看到并联补偿电容投入时,并网点的电压和电流会发生持续性的谐波谐振。图中Vpcci,Ipcci,Iri分别为i相公共耦合点电压、电流和转子电流；Ps和Qs分别为DFIG系统有功和无功功率；Te为电机电磁转矩。

表1给出了图5(a)中不同区间内高频谐振频率与理论分析的对比。从表1中可以看到,当并联补偿电容增大即并联补偿度减小时,谐振频率会随之减小,这与1.3节中附录A图A1的分析是一致的,同时对比仿真中系统实际发生的谐振频率与理论分析得到的谐振频率,可以看出谐振频率偏差不超过2.5%,这也验证了前文中谐振机理理论分析的正确性。

图5(b)给出了本文提出的高频谐振抑制策略下DFIG系统的运行波形,其中6 s之前系统并联补偿电容为7.5 μF,谐振频率为535 Hz,此时并网点谐波电压及电流含量为24.07%和15.5%,转子电流谐波含量为13.43%,有功功率和无功功率最大波动分别为0.75 MW和0.55 Mvar,转矩最大波动为2 795 N·m。6 s时加入本文的HFR抑制策略,系统能在0.01 s内实现对谐振的抑制,此时公共耦合点谐波电压和电流含量分别为3.50%和0.94%,转子电流谐波含量为0.49%。6.06 s时,并补电容从7.5 μF变为3.75 μF,由于本文所提出的HFR抑制策略具有较好的适应能力,DFIG系统可迅速恢复稳定运行,此时PCC处电压和电流谐波含量分别为2.48%和1.03%,转子电流谐波含量为0.54%,有功功率波动为84 kW,无功功率波动为74 kvar,转矩波动降低为243 N·m,这说明本文所提控制策略可在系统并联补偿度改变时具有优良的适应能力。

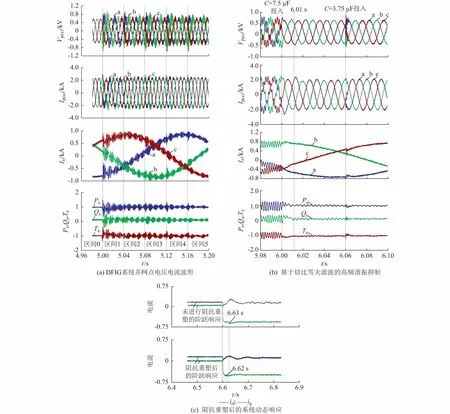
图5 阻抗重塑后的系统运行波形Fig.5 Operation waveforms of system after impedance reshaping

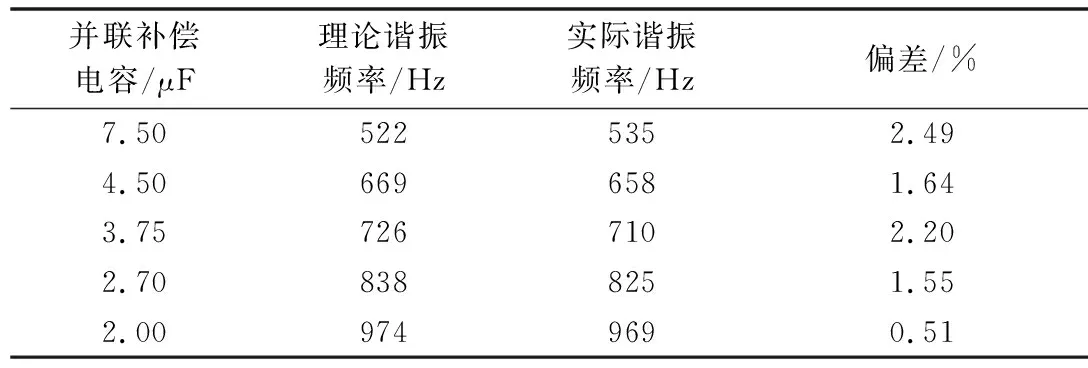
并联补偿电容/μF理论谐振频率/Hz实际谐振频率/Hz偏差/%7.505225352.494.506696581.643.757267102.202.708388251.552.009749690.51

与附录A图A2中系统并补度改变时再次出现的谐振情况相比,图5(c)中DFIG系统可在7 ms内恢复稳定运行,表明DFIG系统能够有效地应对系统并联补偿度的变化,这是因为DFIG系统在高频段都有足够的相位裕度,从而提升了对电网并补度变化的适应能力。同时,本文所提控制策略不会影响基频控制,HFR抑制过程中DFIG系统仍能稳定向电网输送功率,并保持稳定的电磁转矩。

图5(c)则给出了阻抗重塑前后的基频电流控制阶跃响应,可以看到在加入本文阻抗重塑策略以后,系统的动态响应略微提升,阶跃上升时间缩短了10 ms,验证了动态特性分析的正确性。

4 结语

本文深入分析并联补偿度变化时,由于频率检测环节性能下降所导致DFIG系统HFR抑制失效的问题,进而提出了基于阻抗重塑的DFIG系统HFR抑制策略,此策略可省去谐振频率检测环节,避免了并联补偿度改变时HFR抑制失效的问题,提升了DFIG对并补度变化的并补电网适应能力。本文通过分析对比2 MW风机阻抗重塑前后的输出阻抗,并结合仿真结果验证了提出HFR抑制策略的有效性和正确性。由于本文的研究中并补电网为理想电网,而在具有并联补偿的实际电网中还将存在谐波或不平衡的电网电压分量,因此在谐波或不平衡电网下并联补偿与双馈风力发电系统的交互作用仍有待进一步的研究。

本文受到国家自然科学基金(51577174)和风力发电系统国家重点实验室开放基金(2016001)资助,特此感谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。