基于广义短路比的电力电子多馈入系统小干扰概率稳定评估
王冠中, 董 炜, 辛焕海, 朱承治
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网浙江省电力有限公司, 浙江省杭州市 310007)
0 引言
电力电子设备具有很强的灵活性和可控性,被广泛应用于可再生能源并网、直流输电等领域[1]。随着光伏、风电等可再生能源在电力供给中比重不断增大[2],更多电力电子设备接入交流电网,形成了电力电子设备多馈入系统(后文简称多馈入系统)。多馈入系统中电力电子设备总容量持续上升,引起交流电网电压支撑能力的相对下降,交流电网相对变弱,导致设备间、设备与系统间的耦合加剧,也增加了发生系统振荡的可能[3-5]。
准确评估多馈入系统中交流电网的强度,以及分析设备间的相互作用,是抑制振荡和保证多馈入系统安全稳定运行的必要前提[6-8]。工程上常用短路比(short circuit ratio,SCR)来分析电力电子设备馈入交流系统时交流电网的相对强度。文献[9-10]研究了电力电子设备单馈入系统的稳定性与短路比的关系;文献[11-12]从静态电压稳定的角度定义了多馈入直流系统的短路比指标,其本质是利用电压相互作用因子将多馈入直流折算到某一条直流上,但它不适用于“非对称系统”;文献[13]定义的传统直流多馈入系统广义短路比(generalized short circuit ratio,gSCR)从机理和数学上实现了单馈入和多馈入系统强度量度指标的统一;文献[14]从小干扰稳定的角度定义了电力电子多馈入系统的广义短路比,为多馈入系统小干扰稳定裕度提供了解析化的分析工具。
虽然电力电子多馈入系统的广义短路比可以解析化地分析系统小干扰稳定裕度,然而,系统受可再生能源功率随机波动的影响,运行时稳定裕度存在不确定性。在确定运行条件下确定的广义短路比无法定量量化随机条件下的小干扰稳定裕度。因此,计算多馈入系统小干扰概率稳定裕度对于多馈入系统动态稳定性评估具有重要意义。
针对电力电子多馈入系统小干扰概率稳定裕度评估问题,首先将文献[14]中的广义短路比推广到广义运行短路比(generalized operation short circuit ratio,gOSCR),从而能够量度电力电子设备任意输出功率时的系统小干扰稳定裕度;其次,利用广义运行短路比将多馈入系统的小干扰概率稳定裕度评估转化为概率D稳定问题;同时为克服在工程实践中获取输出功率准确概率分布的困难,采用期望和方差等部分概率信息来描述系统随机性,在此基础上结合广义矩理论将矩阵概率D稳定问题转化为半定规划进行求解。最后,通过算例说明所提方法的有效性。
1 广义运行短路比指标
1.1 多馈入系统广义短路比回顾
考虑由n台电力电子设备馈入的交流系统,如图1所示,其中第i台电力电子设备端口电压的幅值和相角分别为Ui和θi,所接入的交流电网母线的等值内电势为Ei∠θ0。

图1 电力电子多馈入系统Fig.1 Power electronic based multi-infeed system
文献[14]基于以下三个假设条件,从小干扰稳定的角度提出多馈入系统广义短路比指标。
假设1:多馈入系统的n台电力电子设备都是“相似的”,即控制策略、以自身容量为基准的主电路参数都相同。
假设2:送端等效交流网络是连通的,且网络中电阻和电容均远小于电感。
假设3:在稳态时(即潮流方程解),电力电子设备之间的联络线功率远小于其传输极限。
根据以上假设,广义短路比的值γgSCR被定义为交流系统扩展雅可比矩阵的最小特征根,即
γgSCR=minλ(Jeq)
(1)
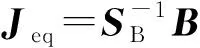
在额定工况下,广义短路比理论实质是将多馈入系统解耦成等效单馈入系统(如图2所示),而单馈入系统的特征方程与短路比数值γSCR(i)存在如下显函数关系[14]:
(2)
式中:γSCR(i)=λi(Jeq)为解耦后的等效短路比,其中λi(Jeq)为矩阵Jeq的第i个特征根;a(s)和b(s)只跟交流网络参数有关,对于假设1中的相似设备,解耦后得到的单馈入系统特征方程中a(s)和b(s)都是相同的。

图2 多馈入系统解耦示意图Fig.2 Decoupling schematic diagram of multi-infeed system
式(2)为第i个单馈入系统的闭环特征方程,根据已有研究可知:短路比的值越大,说明电力电子设备所连接的交流电网就越强,则系统越稳定;反之,系统容易出现Hopf分岔而发生小干扰失稳问题[15-16]。
由于广义短路比只与交流网络的导纳矩阵和接入的电力电子设备额定容量相关,且是一个反映系统小干扰稳定裕度的静态指标,因此具有计算过程简单,便于工程应用的优势。
1.2 广义运行短路比
文献[14]在额定工况下推导了广义短路比,本文类比直流系统将广义短路比推广到非额定工况下的广义运行短路比。
逆变器采用基于锁相环的双环控制策略,外环为PQ控制,详见图3,并假设系统正常运行时功率因数为1。图中:PLL表示锁相环;PI表示比例—积分;SVPWM表示空间矢量脉宽调制;PCC表示公共耦合点。根据上述条件,基于文献[17-18]中的小信号模型,电力电子设备侧的雅可比传递函数矩阵可表示为(推导过程见附录A)[18]:
(3)
式中:Pi为电力电子设备输出功率以单位容量为基准的标幺值;Ui,ΔUi和Δθi分别为第i台电力电子设备并网点处的电压幅值及其变化量和相角变化量。
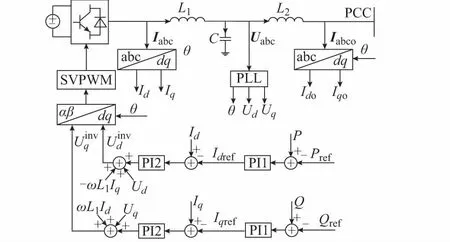
图3 单馈入系统典型控制框图Fig.3 Block diagram of a single infeed system
根据假设1,每台设备的雅可比传递函数矩阵中Ji(s)均相同[14]。此外,式(3)中的传递函数矩阵已经将输出功率Pi作为公因数从矩阵元素中提取出来,提取公因数后的矩阵元素由电力电子设备的控制参数决定,与输出功率无关[18]。
参考文献[14]中的交流电网雅可比传递函数矩阵,并结合式(3),多馈入系统闭环特征方程表示为:

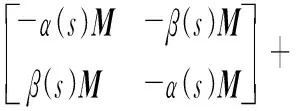
(4)
式中:⊗表示Kronecker积;M=(Mij),其中Mij=UiUjBijcosθij;det(·)表示求行列式;Pi=diag(Pi);α(s)=1/[(s/ω0)2+1],其中ω0为工频角速度;β(s)=(s/ω0)/[(s/ω0)2+1]。


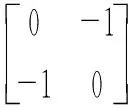
(5)
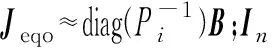
类比文献[14],对Jeqo进行特征根分解。将特征值按照从小到大顺序排列0<λo1<λo2≤…≤λon,则式(5)可看作多个单馈入系统特征方程的积,即
co1(s)co2(s)…con(s)=0
(6)
其中

(7)
定义广义运行短路比的数值表示γgOSCR为拓展导纳矩阵Jeqo的最小特征值,即
γgOSCR=minλ(Jeqo)
(8)

此外,由于节点导纳矩阵B由网络参数决定,当考虑功率的不确定性时,拓展导纳矩阵Jeqo可看作是由P中元素决定的矩阵Jeqo(P)。在实际系统运行中,P反映了设备的输出功率,即光伏、风机等可再生能源发电设备的有功输出。同时,类似于交直流系统短路比,运行广义短路比广义运行短路比存在临界值γCgOSCR,对应着多馈入系统一对共轭特征根到达虚轴的运行条件,而广义运行短路比与γCgOSCR之间的差可以被看作是多馈入系统小干扰稳定裕度的大小[18]。
2 概率稳定裕度及求解方法
为保证多馈入系统运行时能具有一定的小干扰稳定裕度,一般要求广义运行短路比大于某个临界值γ(γ>γCgOSCR)。然而,可再生能源发电功率P具有随机性,在实际系统运行时矩阵Jeqo(P)的特征值存在不确定性,因此仅依靠广义运行短路比难以评估系统失稳风险。针对电力电子设备输出功率的不确定性,本文提出概率稳定裕度计算问题,即求出γCgOSCR<γ的最大概率,用以评估系统小干扰稳定裕度不足的风险。

2.1 D稳定和概率D稳定
首先定义矩阵D稳定。
定义1:当P存在不确定性时,若矩阵Jeqo(P)的所有特征值都在区间D内,则矩阵Jeqo(P)被称为D稳定。
矩阵Jeqo(P)是否D稳定可通过求解式(9)判断,若最优解为0,则矩阵是D稳定的[21]:
(9)
式中:Δ为P中元素Pi所在的不确定集;Dc为区间D的补集。
由于拓展导纳矩阵Jeqo的特征值都是实数[13],因此本文中的D都是实数区间。此外,Δ为闭合的半代数集[22],具体形式为:
Δ={P∈Rn:gi(P)≥0,i=1,2,…,m}
(10)
式中:gi为关于P中元素的实值多项式函数。
接下来简单阐述式(9)的作用原理:只有当Jeqo(P)为D稳定,即Dc中不包含Jeqo(P)的任何一个特征值时,矩阵Jeqo(P)-λIn才能非奇异,此时x只能是零向量。所以当最优解为0时,矩阵Jeqo(P)在Δ上是D稳定的。
接下来定义概率D稳定。
定义2:当P为具有部分概率信息的随机变量时,概率D稳定,即求出Jeqo(P)的特征值不在区间D中的最大概率:

(11)

而概率计算式(11)可以看作式(9)在概率空间上的积分结果[22]:
(12)
式中:ρP,x,λ为关于P,x,λ的联合概率分布。
式(12)中的前两条约束均是表达概率分布ρP,x,λ在概率空间上的积分为1,这与一般概率分布的性质相吻合;第3条约束中的fi(P)代表仅与随机变量有关的多项式,用来计算期望或方差,如对P中第i个变量求期望,则fi(P)=Pi,若对该变量求方差,则fi(P)=(Pi-ui)2;第4条约束是D稳定问题(9)中第2个约束条件在概率空间上的投影。
此外,对式(12)的有效性解释如下。当矩阵Jeqo(P)不满足D稳定时,‖x‖2=1,否则‖x‖2=0,因此,式(12)中的目标函数是对‖x‖2在整个概率空间上进行的积分,积分结果就是矩阵Jeqo(P)不满足D稳定的概率。

2.2 求解概率D稳定问题的广义矩方法
式(12)是一个有着有限约束条件和无限决策变量的半无限线性规划,本节利用广义矩理论将式(12)转化为半定规划。
引入增广向量变量z=[x,P,λ]∈Rnz,nz=2n+1,并令h(z)=‖x‖2,fi(z)=fi(P),以变量z和联合概率分布ρz的形式重写式(12)后得到:
(13)
式中:Z={z∈Rnz:qj(z)≥0,j=1,2,…,nq}定义了概率分布ρz在概率空间上的支撑集[22],也是闭合的半代数集,由D稳定中的(Jeqo(P)-λIn)x=0和Δ两部分构成,其中qj为多项式函数,用来描述Δ中的gi以及方程组(Jeqo(P)-λIn)x=0的所有等式方程。
式(13)所定义的优化问题和基于矩量理论的电力系统全局优化方法[23-24]都属于广义矩问题[25]的数学范畴。求解这类问题的一般方法是先将概率分布上的积分投影成矩量变量,然后构造矩量矩阵和局部矩阵[23]来把概率分布限定在支撑集上,最后求解所得半定规划问题[24]。

(14)


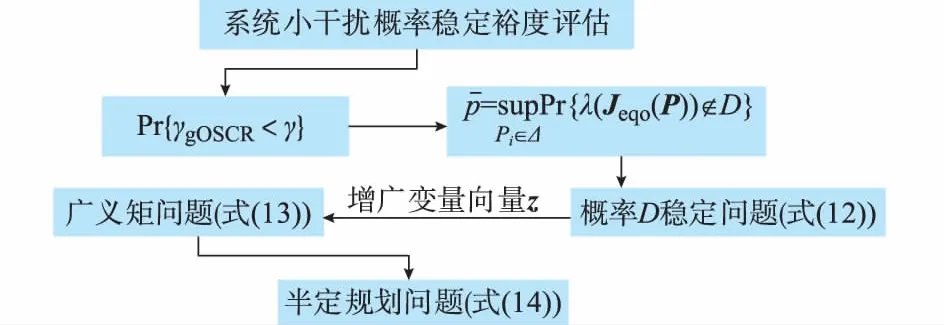
图4 概率稳定评估流程Fig.4 Evaluation process of probabilistic stability
2.3 多馈入系统小干扰概率稳定裕度评估步骤
实际系统运行时的小干扰稳定评估步骤如下。
步骤1:输入交流电网等值后的多馈入系统线路结构和参数,根据设备自身特性确定广义运行短路比的临界值γ。
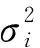
步骤3:按照图4所示概率稳定评估流程计算出下一运行时段γgOSCR<γ的最大风险。
步骤4:根据计算得到的多馈入系统小干扰概率稳定裕度对多馈入系统的运行状况做出适应性评价。
3 算例分析
本节首先验证广义运行短路比能够度量多馈入系统小干扰稳定裕度。其次,考虑电力电子设备输出功率的随机性,利用广义矩理论求解小干扰概率稳定裕度,并分析不同方差数据下的概率变化。最后分析了网络参数和结构对多馈入系统小干扰概率稳定裕度的影响。
算例分析基于MATLAB平台,使用Simulink验证多馈入系统广义运行短路比的有效性。利用GloptiPoly 3[26]求解器对广义矩问题(式(13))进行直接建模和求解。计算条件为一台具有Intel Pentium G3260 3.3 GHz CPU和4 GB内存的双核计算机。
3.1 系统基本参数
网络结构采用图1所示的三馈入系统拓扑,设备参数、电力电子设备的额定功率和交流网络参数见附录B。逐点试探得到单馈入系统的临界短路比为2。
3.2 广义运行短路比有效性分析
将节点2,3上的电力电子设备保持额定功率,改变节点1上的电力电子设备输出功率,输出功率变化时广义运行短路比和系统最危险特征值的变化趋势见图5。
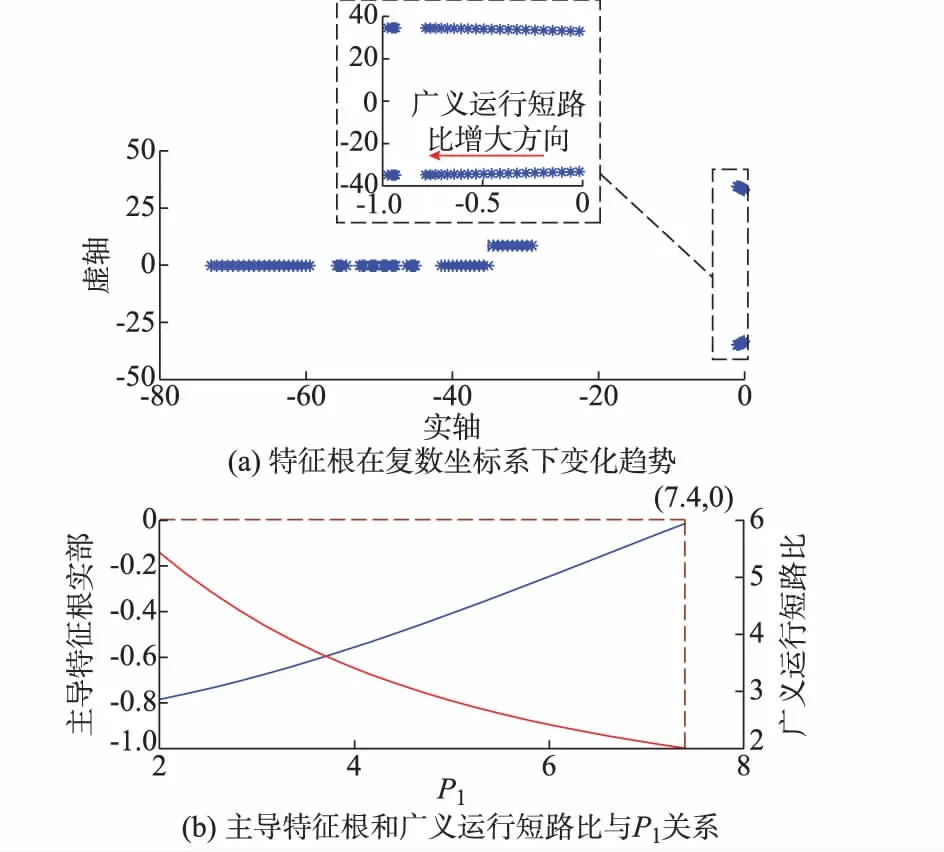
图5 广义运行短路比和最危险特征根比较Fig.5 Comparison of gOSCR and critical eigenvalue
由图5(b)可知,当节点1设备输出功率增加后,多馈入系统的广义运行短路比呈下降趋势,而多馈入系统的最危险特征根实部出现上升趋势(即图5(a)中特征根随广义运行短路比增大而远离虚轴)。当节点1设备的输出功率增大到7.4(标幺值)时,三馈入系统的广义短路比到达临界值2,此时,系统最危险特征根实部为0。仿真结果表明,当设备输出功率增加时,广义运行短路比减小,系统小干扰稳定裕度下降。
3.3 基于广义矩的概率计算方法有效性分析
本节通过与正态分布下γgOSCR<γ的概率Pr{γgOSCR<γ}进行比较,说明所提基于广义矩理论的概率计算方法有效。

图6 广义矩与正态分布结果比较Fig.6 Result comparison of generalized moment and normal distribution
图6中分别是基于广义矩理论的概率结果和正态分布下1 000次蒙特卡洛模拟结果,二者都随着γ的增大而变大,说明设置γ越大则实际系统广义运行短路比低于γ的概率也越大。
基于广义矩理论求sup Pr{γgOSCR<γ}的方法不依赖准确的概率分布信息,只利用随机变量的区间、期望和方差等部分信息,因此对可能的概率分布具有鲁棒性。从图4也可以看出,广义矩方法求出的sup Pr{γgOSCR<γ}比正态分布下的Pr{γgOSCR<γ}更为保守,说明了该方法有效且对概率分布具有鲁棒性。此外,广义矩方法每次计算时间大约为2 s,计算效率较高,有助于实现多馈入系统动态稳定性的快速评估。
3.4 方差大小对广义运行短路比概率的影响

图与结果比较Fig.7 Result comparison of and
3.5 网络参数对广义运行短路比概率的影响
本节通过改变三馈入系统的线路阻抗参数,分析网络参数对广义短路比概率的影响。
经过筛选,以节点2和节点3之间的线路参数作为控制变量,比较γgOSCR<6.64的最大概率sup Pr{γgOSCR<6.64}。阻抗标幺值分别为0.04,0.08,0.12时,对应的Pr{rgOSCR<6.64}分别为0.59,0.69,0.80。由此可知,增大节点2,3之间的线路阻抗,sup Pr{γgOSCR<6.64}也随之增加,说明节点2,3之间的线路阻抗越大,多馈入系统小干扰稳定裕度不足的风险也越大,该线路阻抗值与系统风险呈正相关。进一步,将节点1与节点2上的电力电子设备交换位置,分析网络结构变化对广义短路比概率的影响。在原始系统中计算出的sup Pr{γgOSCR<6.58}为0.67,而交换节点1和2设备后,sup Pr{γgOSCR<6.58}为1。因此,设备安装位置不同而带来的不同网络结构对广义短路比的概率也会产生较大的影响。
4 结语
本文采用电力电子多馈入系统广义运行短路比量化实际系统运行时的小干扰稳定裕度。同时,针对电力电子设备输出功率具有随机性的问题,利用概率D稳定计算广义短路比小于某个临界值的最大概率,并利用广义矩理论求解。由分析可知,概率D稳定方法所得结果较正态分布更为保守,说明所提方法对概率分布具有较好的鲁棒性;多馈入系统网络参数会影响系统稳定裕度不足的概率,电力电子设备安装位置带来的网络结构变化也会改变系统概率稳定裕度。
本文所提出的电力电子多馈入系统小干扰概率稳定裕度评估方法,为可再生能源接入交流系统的动态稳定性评估供了必要的参考。
本文受到国家自然科学基金资助项目(51577168)支持,特此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

