钢丝绳拉伸疲劳寿命仿真分析与试验研究

杜文正， 马保珠， 曹大志， 付广磊

(火箭军工程大学 二系，西安 710025)

钢丝绳由于具有承受拉伸载荷能力强、容易弯曲卷绕、便于在较大距离范围内传递牵引动力等突出优点，被广泛应用于各种起重机械的起升机构中。同时，由于起重机械是一种典型的间歇重复动作机械设备，在不断进行的负载提升、下降、卸载过程中，起升机构的钢丝绳在卷筒、滑轮组构成的卷绕系统中运行时也反复受到拉伸、弯曲载荷的作用，使得疲劳损坏成为钢丝绳比较常见的损伤失效模式。即使钢丝绳的载荷幅值远低于其静态破断拉力，钢丝绳在长期使用后依然会由于疲劳逐渐出现断丝，严重时甚至导致钢丝绳突然断裂[1]，可能引发的机械设备安全事故以及带来的经济损失将是十分巨大的。在航天、矿山、冶金、化工等对起重机械安全性具有较高要求的行业中，钢丝绳等重要承载零部件的疲劳失效一直是受到重点关注的问题，准确掌握钢丝绳的疲劳失效规律，对合理制定设备维护周期、预防事故发生具有重大的意义。

许多学者对钢丝绳的疲劳失效进行了分析研究。鲁信辉等[2]利用SolidWorks建立了6×7+IWS钢丝绳模型，进行了轴向拉伸的有限元和疲劳分析，研究了应力与疲劳的关系。贾小凡等[3]研究了钢丝绳的弯曲疲劳，探究了钢丝绳的弯曲疲劳损伤机制。胡茂[4]通过理论分析和试验研究了滑轮直径对钢丝绳疲劳寿命的影响。Wang等[5]分析了不同运动参数对煤矿用钢丝绳微动疲劳寿命的影响。Peterka等[6]对某型钢丝绳进行了疲劳试验和金相分析，发现失效的原因是生产商将不同等级的钢丝混用，降低了钢丝绳的强度。Giglio等[7]建立了直升机救援用钢丝绳在拉伸载荷和弯矩作用下的应力应变分析和疲劳寿命预测的数学模型，分析了钢丝绳的应力应变和疲劳寿命，并与试验结果进行了仔细地对比，提出了一个可信度较高的钢丝绳寿命预测方法。倪响[8]研究了钢丝绳表面断丝，表面磨损和表面腐蚀对钢丝绳弯曲疲劳性能的影响。任志乾等[9]建立了钢丝绳的弹塑性损伤本构模型，为研究钢丝绳的寿命提供了基础。Wang等[10-11]通过钢丝微动试验，研究了钢丝的破坏机制。赵维建等[12]以矿用钢丝为研究对象，探究了在碱性腐蚀环境下，接触载荷对钢丝微动磨损的影响，分析了钢丝微动磨损和疲劳断裂机理。Cruzado等[13]结合有限元磨损模型和临界平面SWT损伤积累的方法，提出了一种预测细钢丝微动磨损引起裂缝的方法。

尽管对疲劳仿真分析方法的研究不断深入，但为了准确掌握材料疲劳失效规律，疲劳试验是一个非常重要的途径。由于中大型起重机械采用的钢丝绳承载绳股及钢丝数目较多、内部结构比较复杂，同时钢丝绳内部的钢丝之间存在复杂的接触挤压和滑动摩擦，使用钢丝绳进行疲劳试验时，试验结果会有较大的分散性，为了获取比较准确的疲劳寿命规律，往往需要进行大量的试验。此外起重机钢丝绳的强度高，对试验设备的加载能力也有较高要求，如果单纯依靠试验研究手段，试验成本将会比较大，需要结合数值仿真及实验验证的方法来提高研究效率。

某桥式起重机起升机构采用了公称直径12 mm，破断拉力103 kN的6×36 WS钢丝绳。由于某一场所对起吊安全性有很高的要求，为了较为准确地掌握该种钢丝绳的疲劳寿命规律，本文综合利用有限元疲劳仿真和疲劳试验的方法对钢丝绳拉伸疲劳进行了研究。为了提高试验的针对性和试验效率，首先进行钢丝绳在拉伸载荷下的有限元分析，找出处于最大应力状态的钢丝，对其进行拉伸疲劳试验，由试验数据得到钢丝的疲劳寿命曲线。并利用钢丝疲劳寿命曲线进行钢丝绳拉伸疲劳寿命仿真分析，得出6×36 WS钢丝绳的疲劳寿命曲线。最后通过钢丝绳在几种典型载荷幅值条件下的拉伸疲劳试验对仿真分析结果进行验证。本文得到的6×36 WS钢丝绳的疲劳寿命曲线可为开展实际服役结构中的钢丝绳疲劳失效预测打下基础。

1 钢丝绳的有限元分析

钢丝绳有限元分析是疲劳寿命仿真分析的基础，主要目的是获取钢丝绳在轴向拉伸作用下的应力分布情况，提供钢丝绳疲劳仿真所需的有限元结果文件，并找出应力最大部位所在的钢丝，作为钢丝疲劳试验选材的依据。

1.1 钢丝绳的几何模型

建模对象为6×36 WS右交互捻圆股钢丝绳，公称直径为12 mm，外观如图1所示。

钢丝绳捻距为75.6 mm，截面形状如图2所示。钢丝绳由外围的6个绳股和中央的PPC绳芯组成。每个绳股又由三层外围钢丝绕一根股芯钢丝缠绕而成。其中，股芯钢丝直径为0.75 mm；与股芯接触的第一层有7根钢丝，直径为0.55 mm；第二层由7根直径为0.40 mm和7根直径为0.55 mm的钢丝组成；绳股的最外层有14根钢丝，直径为0.70 mm。

图1 某型起重机用钢丝绳Fig.1 The wire rope of a crane

图2 钢丝绳截面图Fig.2 The cross section of the wire rope

由于钢丝绳的绳股轴线是螺旋线，钢丝轴线是围绕绳股轴线的二次螺旋线，很难在几何建模软件中直接扫描生成，必须通过数学计算为几何建模提供每一根钢丝的轴线坐标参数。绳股轴线坐标和钢丝轴线坐标均采用三维笛卡尔坐标表示，绳股轴线坐标表示为[xcycz]T，钢丝轴线坐标表示为[xyz]T，其中的z为钢丝绳轴线上的位置坐标，计算时以z坐标为自变量来确定x轴和y轴坐标。

右旋绳股轴线坐标计算公式为

(1)

绳股内部左旋钢丝相对于绳股中心的相对坐标计算公式为

(2)

其中，r为绳股中心相对于钢丝绳中心的分布圆半径，rs为绳股内部某一层钢丝相对于绳股中心的分布圆半径。p和ps分别为绳股捻距和绳股内部的钢丝捻距。α0为绳股轴线起始点在钢丝绳模型端面上的初始方位角，αs0为该绳股内钢丝轴线起始点相对于绳股轴线起始点的初始方位角。将钢丝相对于绳股中心的相对坐标变换为相对于钢丝中心的全局坐标的计算公式为

(3)

确定了所有绳股轴线和钢丝轴线坐标参数序列后，在MATLAB中编程生成各根钢丝的空间坐标，导入SolidWorks中，利用其扫描功能建立钢丝绳一个捻距的几何模型，如图3所示。

图3 SolidWorks建立的钢丝绳几何模型Fig.3 The cross section of the wire rope

1.2 材料属性与网格划分

根据钢丝绳结构的对称性，将1/6捻矩的钢丝绳作为导入到ABAQUS软件中进行分析。在ABAQUS环境中对几何模型赋予材料属性，具体参数如表1所示。

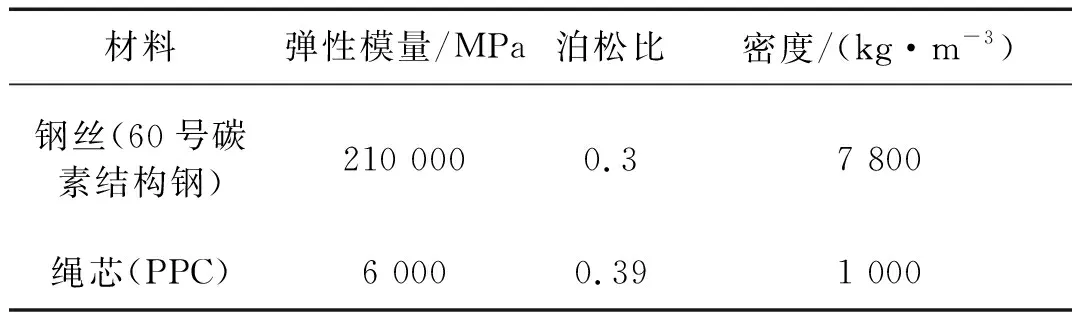
表1 钢丝绳的材料属性Tab.1 Material properties of the wire rope

采用六面体单元对钢丝绳进行有限元离散，得到的钢丝绳有限元网格如图4所示。经收敛性测试，钢丝绳有限元模型共有1 124 157个单元，1 315 106个节点。

图4 6×36 WS钢丝绳有限元网格Fig.4 Finite element mesh of 6×36WS wire rope

1.3 接触属性

由于钢丝与绳芯的材料不同，故钢丝绳中存在着2种类型的接触对，即钢丝与绳芯接触对，钢丝与钢丝接触对，如图5所示。为了更真实地模拟钢丝绳实际受力状况，在接触属性中均定义库仑摩擦。查阅机械设计[14]常用材料的摩擦因数，定义PPC绳芯与钢丝之间的摩擦因数为0.05，定义钢丝与钢丝之间的摩擦因数为0.1。

(a) 钢丝与绳芯接触对(b) 钢丝与钢丝接触对

图5 钢丝绳接触对

Fig.5 Contact pairs of the wire rope

1.4 约束及边界条件

为了便于施加载荷，在钢丝绳前、后两端面中心处分别建立一个参考点，采用运动耦合模式，如图6所示。边界条件[15]设为：固定钢丝绳一端，对钢丝绳另一端施加轴向拉伸载荷4 900 N，模拟钢丝绳在500 kg重物拉伸下的受力状况。

图6 钢丝绳端面耦合约束Fig.6 Coupling constraints of the wire rope’s end face

1.5 钢丝绳应力分析

图7所示为钢丝绳的Von-Mises应力分布云图。整体上，钢丝绳应力分布不均匀，绳芯应力最小。钢丝绳6根绳股空间循环对称，其应力分布也完全相同。由于钢丝绳两端的约束效应，两端存在明显的应力集中，应力比其他区域较大。观察单根钢丝可以发现钢丝两端由于受到约束的影响，应力较大，其他区域应力同样呈不均匀分布，钢丝与钢丝接触的部位应力较大。

钢丝绳中部区域的钢丝之间自由接触，受端面边界条件的影响较小，故取钢丝绳轴向1/2长度处横截面上的应力分布(图8)进行分析。可以看出，整个截面上，最大应力位于相邻两个绳股接触区域，即钢丝绳绳股形成的螺旋形沟槽的谷部。绳芯应力最小，绳股上应力呈波浪状分布，绳股外围一圈钢丝与绳股内部钢丝相比应力较大。每根钢丝横截面上的应力呈层状分布，钢丝间接触区域应力较大。

图7 钢丝绳Von-Mises应力分布Fig.7 The Von-Mises stress distribution of the wire rope

图8 钢丝绳横截面上的应力分布Fig.8 The stress distribution at cross section of the wire rope

2 钢丝疲劳寿命试验

钢丝试件的疲劳寿命曲线是钢丝绳疲劳寿命仿真分析的基础，钢丝材料为60号碳素结构钢，经过冷拔处理，钢丝公称抗拉强度为1 770 MPa，由于标准材料数据中缺乏此类实际结构部件的疲劳寿命数据，其疲劳寿命曲线需通过试验获得。

根据钢丝绳有限元分析的结果可知，钢丝绳承受轴向拉伸载荷时，最大应力位于绳股与绳股接触部位的钢丝上，此处为绳股表层钢丝，直径为0.7 mm。因此疲劳试验的钢丝试件采用直接从6×36 WS钢丝绳绳股表层抽取的0.7 mm直径钢丝。

2.1 试验方法

试验方法参照GBT 3075—2008《金属材料疲劳试验轴向力控制方法》，试验环境温度为常温，试验设备使用Instron E10000电子疲劳试验机，试验状态如图9所示。试件为6×36 WS钢丝绳绳股表层抽取的长度为200 mm的0.7 mm直径钢丝。钢丝试件通过专用钢丝夹具加持固定在试验机上，标距段长度为60 mm，夹具夹持部位采用特殊的曲面设计，可以有效避免试件夹持固定部位的应力集中。

图9 钢丝疲劳试验状态Fig.9 The state of the wire fatigue test

钢丝公称抗拉强度为1 770 MPa，横截面积为0.38 mm2，对应的破断拉力为681 N。钢丝轴向拉伸疲劳试验交变载荷的最大值Smax以破断拉力Sb的90%为基准，并按10%递减的规律设定。交变载荷的最小值Smin按应力比R=0.4确定，即Smin=0.4Smax，每组载荷测试5个试件。试验过程发现，当Smax小于0.7Sb时，结果出现了异常，为查明原因，当载荷为0.6Sb和0.5Sb时增加了一组试件数。试验的载荷值及试样数如表2所示。

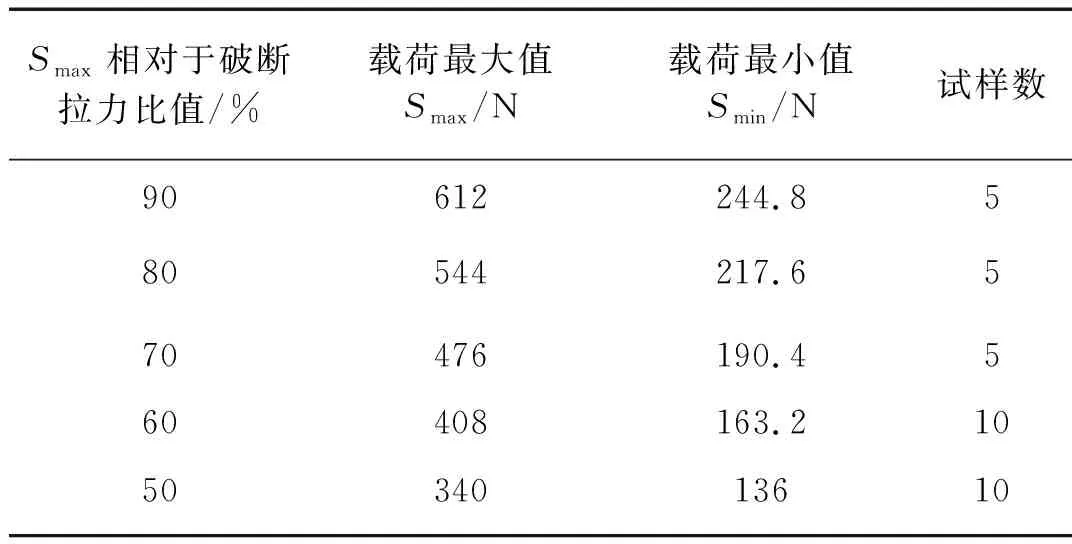
表2 钢丝疲劳试验的载荷值和试件数Tab.2 Load value and wire number of the fatigue test

2.2 试验结果

钢丝疲劳试验结果如图10所示。由图中可以看出，随着载荷减小，疲劳寿命整体上呈逐渐增大趋势，但在Smax小于0.7Sb(476 N)时，疲劳寿命出现一个拐点；另外，Smax等于0.5Sb(340 N)时的疲劳寿命试验结果表现出较大的分散性。

2.3 钢丝试件的载荷寿命曲线

试验过程中，当Smax<0.7Sb时，螺旋形钢丝试件未被完全拉直，疲劳断裂表现为拉伸疲劳与弯曲疲劳的耦合，由于钢丝试件的二次螺旋线形状复杂，使得不同部位的拉伸疲劳和弯曲疲劳的耦合情况并不完全一致，断裂失效部位的随机性导致试验结果表现出较大分散性。因此，能够反映钢丝试件疲劳寿命规律的主要为Smax>0.7Sb的载荷条件下的试验数据，故采用这些数据拟合钢丝材料的载荷寿命曲线。

图10 疲劳试验结果Fig.10 Fatigue test results

由于载荷寿命曲线在循环次数N和交变载荷最大值Smax的双对数坐标系中近似为一条斜直线，因此在该坐标系中可以采用最小二乘法根据试验数据拟合出载荷寿命曲线，从而可以对不同载荷条件下的疲劳寿命进行近似估计。

令x=lgN，y=lgSmax，利用最小二乘法拟合出双对数坐标系中的载荷寿命曲线方程。

(4)

其中

(5)

(6)

(7)

由试验数据拟合载荷寿命曲线在双对数坐标系中直线方程为

y=2.733 7-0.258 7(x-4.385 2)

(8)

根据式(8)可计算出循环次数在103～106范围内对应的Smax坐标数值，相应的载荷寿命曲线如图11所示，为下一步钢丝绳的疲劳仿真分析提供了依据。

3 钢丝绳疲劳寿命仿真与试验分析

疲劳试验是钢丝绳疲劳失效规律和疲劳寿命研究的重要依据。但由于钢丝绳内部结构复杂，不可能保证所有试件的表面状态、内部接触状态、端头固结情况等完全一致，疲劳试验结果会表现出较大的分散性，而且受试验设备加载能力和试验成本等因素的限制，疲劳试验也无法覆盖足够大的载荷范围。因此，为了获得比较完整的钢丝绳疲劳寿命曲线，必须需要借助仿真分析手段。同时，为了保证疲劳仿真分析结果的有效性，需要通过典型载荷条件下的疲劳试验对仿真分析结果进行验证。

图11 拟合的载荷寿命曲线Fig.11 The load life curve

3.1 钢丝绳疲劳寿命仿真分析

3.1.1 仿真参数设定

钢丝绳的疲劳寿命仿真在ABAQUS有限元分析结果的基础上，利用疲劳仿真软件FE-SAFE完成。将钢丝试件的应力寿命数据和有限元分析结果文件导入FE-SAFE中，计算采用Miner法则，并设定不同的载荷比例因子对0.5～11 t载荷条件下的钢丝绳疲劳寿命进行仿真计算。

3.1.2 额定载荷下的疲劳寿命计算结果分析

起重机的最大额定起重量为5 t，其四倍率滑轮组的单根钢丝绳分支最大静载荷为1.25 t，以该载荷条件下的疲劳寿命分析结果为例对钢丝绳内部结构中不同部位的疲劳寿命分布特点进行说明。

图12所示为1.25 t载荷条件下的钢丝绳疲劳寿命云图，该图中疲劳寿命的最小值位于模型两端，这主要是由于边界约束引起的应力集中所致。排除两端受边界效应影响的部分，可以发现疲劳寿命较小的部位主要位于绳股之间相互接触的区域附近。

图12 钢丝绳疲劳寿命分布云图(1.25 t载荷)Fig.12 The fatigue life distribution of the wire rope (1.25 t)

从仿真结果中单独提取出如图13所示的2根相邻的绳股，可以看出在绳股之间相互接触部位，即有限元分析结果中的高应力区域附近，疲劳寿命明显小于其它部位，这与孙土贵等[16]的分析结果是一致的。

图13 两根相邻绳股上的疲劳寿命分布(1.25 t载荷)Fig.13 The fatigue life distribution of two adjacent strands (1.25 t)

图14所示为钢丝绳模型轴向1/2长度处横截面上的疲劳寿命分布情况，该部位受边界效应影响最小，可以看出绳股外层钢丝疲劳寿命较小，且最小值位于相邻两绳股接触部位的钢丝侧面，而绳股内层钢丝以及钢丝绳界面中央的PPC绳芯的疲劳寿命较大，可达到107次以上，即无限循环寿命。

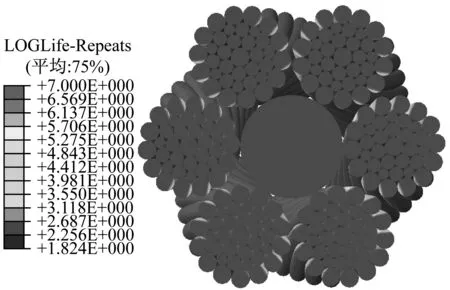
图14 钢丝绳横截面的疲劳寿命分布(1.25 t载荷)

Fig.14 The fatigue life distribution at the cross section of wire rope (1.25 t)

图15所示为疲劳寿命最小的钢丝，即相邻绳股接触部位的表层钢丝的疲劳寿命分布情况，可以看出寿命较短的区域沿二次螺旋线呈非连续分布，与实际的钢丝表面的挤压压痕分布规律一致。

图15 最小寿命钢丝疲劳寿命云图

Fig.15 The fatigue life distribution of the wire having minimal life

3.1.3 不同载荷条件下的疲劳寿命计算结果比较

0.5～11 t不同载荷条件下部分钢丝绳横截面上的疲劳寿命对比情况如图16所示。可以看出，当载荷为0.5 t时，未出现疲劳破坏；当载荷为1 t时，钢丝绳外侧小部分区域出现疲劳破坏；当载荷达到1.1 t时钢丝绳横截面上出现较明显的有限寿命区域。随着载荷的逐渐增大，钢丝绳横截面上疲劳寿命接近107次无限寿命的区域逐渐减小。当载荷达到9 t时，钢丝绳除PPC绳芯外大部分区域出现了疲劳破坏。可见随着拉伸载荷的逐渐增大，钢丝绳疲劳寿命逐渐缩短，疲劳失效区域从绳股外侧逐渐向内部扩展，且钢丝与钢丝接触部位与相邻区域相比疲劳寿命较短。

从不同载荷条件下钢丝绳横截面疲劳寿命计算结果中提取出疲劳寿命的最小数值，得到如表3所示的钢丝绳载荷与疲劳寿命的对应关系。

表3钢丝绳载荷与疲劳寿命对应关系

Tab.3Correspondingrelationshipbetweenloadandfatiguelifeofwirerope

序号钢丝绳载荷/t钢丝绳载荷Smax/kN疲劳循环次数N111107.812988.223768.644658.875549156439.2367329.412582.524.53129219.61172101.7517.152 929111.514.79 744121.2512.2551 848131.211.7673 303141.110.78177 7991519.8521 639160.98.82107170.76.86107180.54.9107

为了便于对钢丝绳进行失效预测和剩余寿命的计算，令x=lgN，y=lgSmax，利用最小二乘法拟合出双对数坐标系中的载荷寿命曲线方程，如式(9)所示。

y=1.417-0.180 2(x-2.856 3)

(9)

即：

Smax5.549 389 57N=5.245 477 16×1010

(10)

根据式(10)可以计算出钢丝绳在不同载荷下的疲劳寿命。

(a)0.5 t

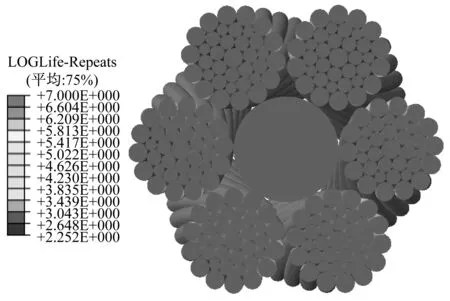
(b)1 t

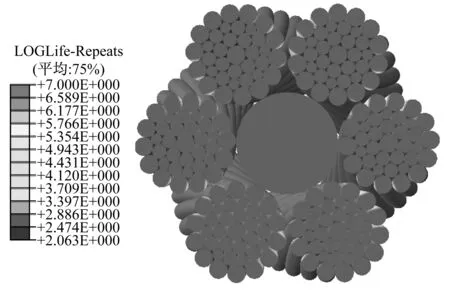
(c)1.1 t

(d)2 t

(e)4 t

(f)9 t

图16 不同载荷条件下的钢丝绳疲劳寿命对比

Fig.16 Fatigue life comparison of wire ropes under different load

3.2 钢丝绳拉伸疲劳试验

3.2.1 试件制备

为了便于与疲劳试验机连接，在被试钢丝绳两端采用巴氏合金浇铸的SOA-03型开式索节制作了连接部件，这种绳端加工方法能够最大限度降低钢丝绳连接部位的强度损失，避免过大的应力集中。试件的钢丝绳部分净长度420 mm，开式索节连接销轴直径26 mm，两端连接销轴距离651 mm。试件外观如图17所示。

图17 试件外观Fig.17 Specimen appearance

3.2.2 试验方法

试验方法参照GBT 3075—2008《金属材料疲劳试验轴向力控制方法》，试验环境温度为常温，试验设备使用MTS Langmark液压伺服疲劳试验机，试验状态如图18所示。

图18 钢丝绳疲劳试验状态Fig.18 The fatigue test state of the wire rope

疲劳试验的载荷频率为10 Hz，交变载荷幅值Sa按起重机起吊最大额定起重量时起升机构四倍率滑轮组单绳承载1.25 t载荷确定，分别取为1.25 t、1 t、0.75 t和0.5 t，交变载荷的最小值Smin均取为0.1 kN，疲劳试验的载荷数值如表4所示。试验过程中每组载荷测试2个试件，当钢丝绳试件出现断丝时停止试验，并记录循环次数；如果循环次数达到106时仍未出现断丝现象，则停止试验。

表4 钢丝绳疲劳试验的载荷值和试件数Tab.4 Load value and number of test pieces of fatigue test

3.2.3 试验结果

疲劳寿命试验结果如表5所示。载荷幅值12.25 kN的1号、2号试件，及载荷幅值7.35 kN的5号试件发生了疲劳断丝现象，其他五个试件循环次数达到106时仍未出现断丝现象。

3.2.4 仿真与试验结果对比

由式(10)可得到由仿真数据用最小二乘法拟合的钢丝绳载荷寿命曲线，并与FE-SAFE仿真数据、疲劳试验数据进行对比分析，如图19所示。可以看出仿真数据拟合的曲线与仿真数据点变化规律基本一致。在钢丝绳额定载荷对应的12.25 kN以下的常用载荷范围内，试验数据、仿真数据和拟合曲线有较好的吻合度，试验数据点均落在拟合曲线附近。由于额定载荷是起重机制造商给出的确保安全使用的最大载荷，因此在起重机正常使用情况下，钢丝绳的实际服役载荷不会超过额定载荷值，如果采用这一拟合的钢丝绳载荷寿命曲线作为对钢丝绳疲劳寿命预测的依据，可以较好地保证寿命预测的准确性。

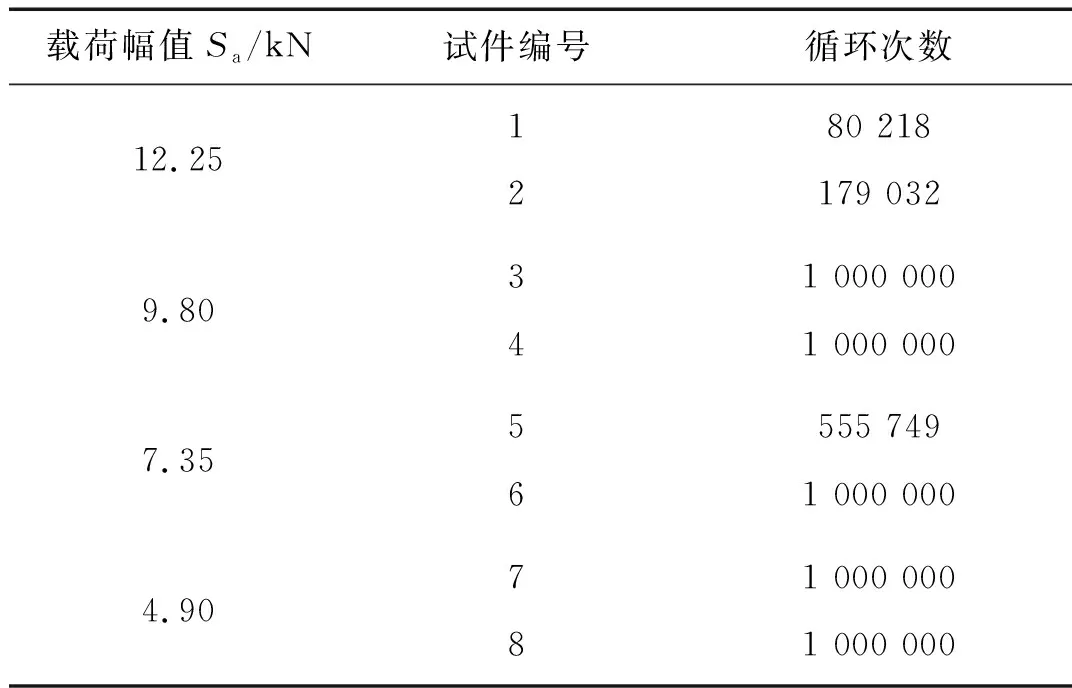
表5 钢丝绳疲劳寿命试验结果Tab.5 Test results of wire rope’s fatigue life

图19 钢丝绳的载荷寿命曲线Fig.19 Load lifetime curve of wire rope

4 结 论

本文分析了起升钢丝绳轴向拉伸状态下的应力分布，在单根钢丝拉伸疲劳试验基础上进行了钢丝绳拉伸疲劳寿命的仿真，拟合出钢丝绳载荷寿命曲线，并与钢丝绳疲劳试验结果进行了对比，可以得出以下结论：

(1) 钢丝绳在轴向拉伸状态下，由有限元仿真结果知最大应力位于相邻两个绳股接触区域，即钢丝绳绳股形成的螺旋形沟槽的谷部，且疲劳仿真结果显示此处最先发生疲劳破坏，寿命最短。

(2) 通过对应力最大的钢丝进行拉伸疲劳试验，得到钢丝试件的疲劳寿命曲线，为钢丝绳的疲劳仿真提供了基础。

(3) 钢丝绳疲劳寿命的仿真结果表明随着拉伸载荷的逐渐增大，钢丝绳疲劳寿命逐渐缩短，疲劳失效区域从绳股外侧逐渐向内部扩展，且钢丝与钢丝接触部位与相邻区域相比疲劳寿命较短。

(4) 对钢丝绳的疲劳寿命进行了仿真分析，得到钢丝绳载荷寿命曲线，并通过疲劳试验进行了验证，疲劳仿真与试验结果具有较好的吻合度，拟合的钢丝绳载荷寿命曲线为疲劳寿命预测提供了依据。