FDZ型防振锤理论计算模型及试验研究

李 黎， 张族炎， 徐宁波， 易勇志

(华中科技大学 土木工程与力学学院，武汉 430074)

特高压输电线路拥有大容量、高效率、远距离等优点，能够优化我国电力资源配置，对于提高我国经济效益和促进开发清洁能源具有重要意义。微风振动威胁着特高压输电线的使用寿命，因此，限制输电导线振动有很重要的实际意义；防振锤作为输电线路一种主要的防振元件，通过和输电线的一起振动，引起锤头的振动，从而使防振锤钢绞线产生变形，变形过程中产生钢绞线材料的能量损耗以及线股之间的摩擦耗能，吸收振动能量，抑制输电线的微风振动。

目前，我国输电线路上应用最多的防振锤是FDZ型防振锤和FR型防振锤。国内外对FR型防振锤耗能特性研究的比较多。Diana等[1-2]建立了FR型防振锤的理论计算模型，并结合试验研究了防振锤的耗能特性。Sauter[3]通过试验和建立数学模型研究了FR型防振锤钢绞线的动力特性。Barry等[4]基于Hamilton原理研究了FR型防振锤的非线性动力特性。Josip[5]利用Abaqus有限元软件建立了FR型防振锤的精细化有限元模型，并结合试验验证了模型的正确性。徐宏波[6]通过理论模型和有限元模型分析了FR型防振锤的锤头质量、钢绞线长度等结构参数对其耗能的影响。罗啸宇等[7]通过测量FR型防振锤在不同激振速度下的阻抗谱，识别其固有频率及阻抗；通过对比防振锤阻抗谱实验与理论模型计算结果，指出现有防振锤线性力学模型的局限性。综述所述，现有关于防振锤的理论计算模型及相关研究都是以FR型防振锤为原型的，而在公开发表的学术文献中，很少有关于FDZ防振锤理论计算模型及耗能特性的研究。

本文根据FDZ防振锤锤头的振动特点，在FR型防振锤理论计算模型的基础上，考虑锤头6个方向的自由度，建立了适用于各类Stockbridge型防振锤的理论计算模型，并结合激振试验[8-11]验证了模型的正确性。

1 FDZ防振锤与FR防振锤的区别

FDZ系列和FR系列防振锤的基本结构分别如图1和图2所示。

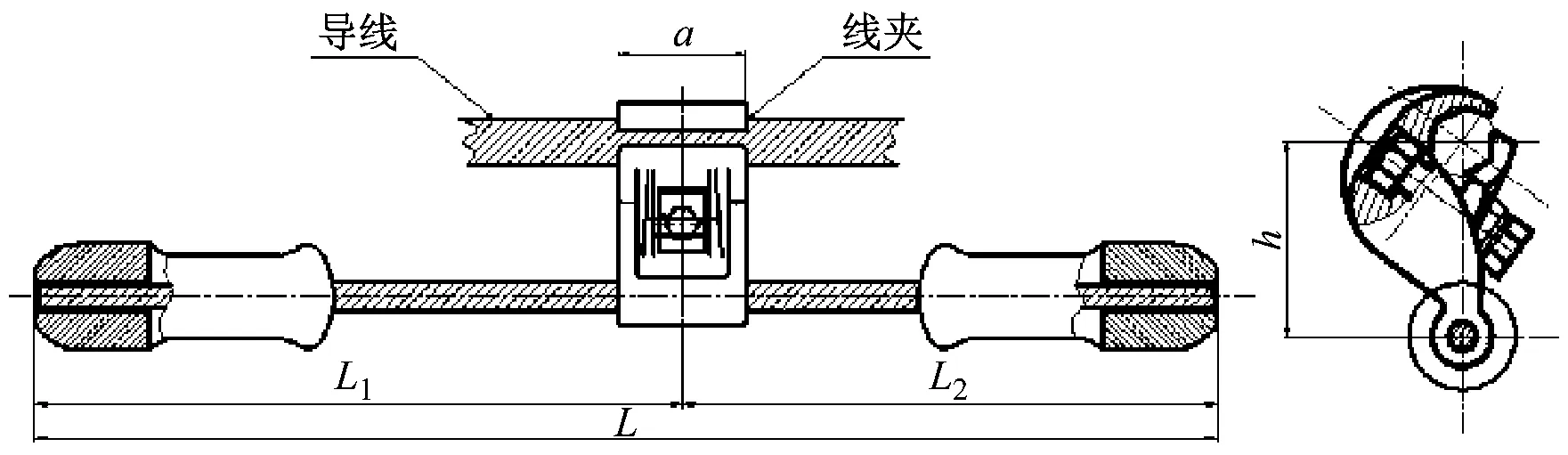
图2 FR型防振锤基本结构图Fig.2 Basic structure of the FR-type damper

由上图我们可以发现，FR型防振锤的锤头关于导线微风振动平面是对称的，而FDZ型防振锤的锤头不对称。由于FDZ型防振锤与FR型防振锤在结构上的不同，从而其防振原理也有所差异。FR型防振锤的多个共振频率[12]主要是来自两边钢绞线的长度不等和两边的锤头质量不等，而FDZ型防振锤的多个共振频率主要是来自两边锤头的多方位振动。

FDZ型防振锤与加拿大和美国用得较多的“扭式防振锤”结构相似，两个锤头都是呈90°布置。这种锤头间呈90°的对称斜度设计，能让锤头多方位振动从而产生多个共振频率，有效吸收不同频率的振动，降低导线疲劳损坏。FDZ型防振锤采用线夹与导线固定，而扭式防振锤采用预绞丝固定。

FDZ型防振锤振动时锤头会有6个自由度，即3个平动自由度和3个转动自由度，现有的防振锤理论计算模型都是在锤头对称的条件下建立的，只考虑了1个平动自由度和1个转动自由度。对FDZ型防振锤而言，需建立6个自由度的防振锤理论计算模型。

2 FDZ防振锤理论计算模型

根据防振锤结构和振动特征，在建立理论计算模型中可做以下假定。

(1)假定防振锤线夹和锤头都是刚性的。

(2)防振锤在振动过程中基本上以正对称模态形式振动，很少出现反对称模态，而且反对称模态由于其振动的反对称性，两边钢绞线对线夹的合力为零，此时防振锤的做功耗能可忽略。所以，以夹固点为界，认为防振锤是由2个单独的子系统组成的。

(3)对钢绞线，忽略其质量，只考虑其弹性。

基于以上假定，结合空间几何、理论力学、结构力学和结构动力学知识，可以建立FDZ型防振锤理论计算模型。

2.1 旋转矩阵

根据FDZ型防振锤锤头特点，建立理论计算模型简图，如图3所示。

图3 计算模型简图Fig.3 The diagram of calculation model

A点为锤头与钢绞线的压结点，C点为锤头的质心。uA，vA，wA分别为A点在x，y，z方向上的位移，αA，βA，γA分别为A点绕x，y，z轴的转角。由于钢绞线和锤头在A点刚接，故锤头在A点出也有相同的位移和转角。

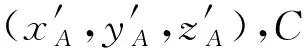
(1)

(2)

这里R是与转角有关的旋转矩阵。

求旋转矩阵R的步骤是先将原始坐标系绕x轴旋转，再将得到的新坐标系绕z轴旋转，最后利用空间绕任意轴的坐标旋转公式求得旋转矩阵R。坐标系旋转过程如图4所示。

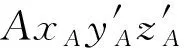
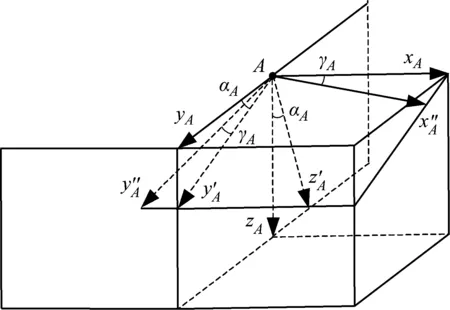
图4 坐标系旋转过程示意图Fig.4 The diagram of coordinate system rotation process

(3)

根据空间绕任意轴的坐标旋转公式，可得旋转矩阵Ry″可表示如下

(4)

其中

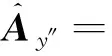
总的旋转矩阵R可表示为

R=Ry″Rz′Rx

(5)

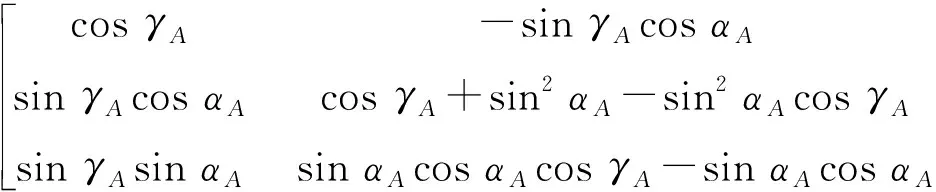
2.2 锤头平动方程

将式(5)代入式(2)可得

(-sinγA)(yC-yA)+(sinβAcosγA)(zC-zA)

(6)

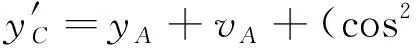
cosαAcosβAsinγA)+cosαAsinγA(cosβA+

cos2αAcos2γA-cos2αAcosβAcos2γA)+sinαAsinγA×

(sinβAsinγA+cosαAcos2γAsinαA-cosαAcosβA×

cos2γAsinαA))(xC-xA)+(cosαAcosγA)(yC-yA)+

(cosαAsinβAsinγA-cosβAsinαA)(zC-zA)

(7)

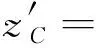
(xC-xA)+(cosγAsinαA)(yC-yA)+(cosαAcosβA+

sinαAsinβAsinγA)(zC-zA)

(8)

又C点的位移可表示为

(9)

根据牛顿第二定律，建立锤头的平动平衡方程如下

(10)

对(uC，vC，wC)T求二阶导数并进行泰勒展开，忽略高阶小量可得

(11)

(12)

(13)

2.3 锤头转动方程

基于空间刚体转动理论，建立锤头转动计算模型，如图5所示。

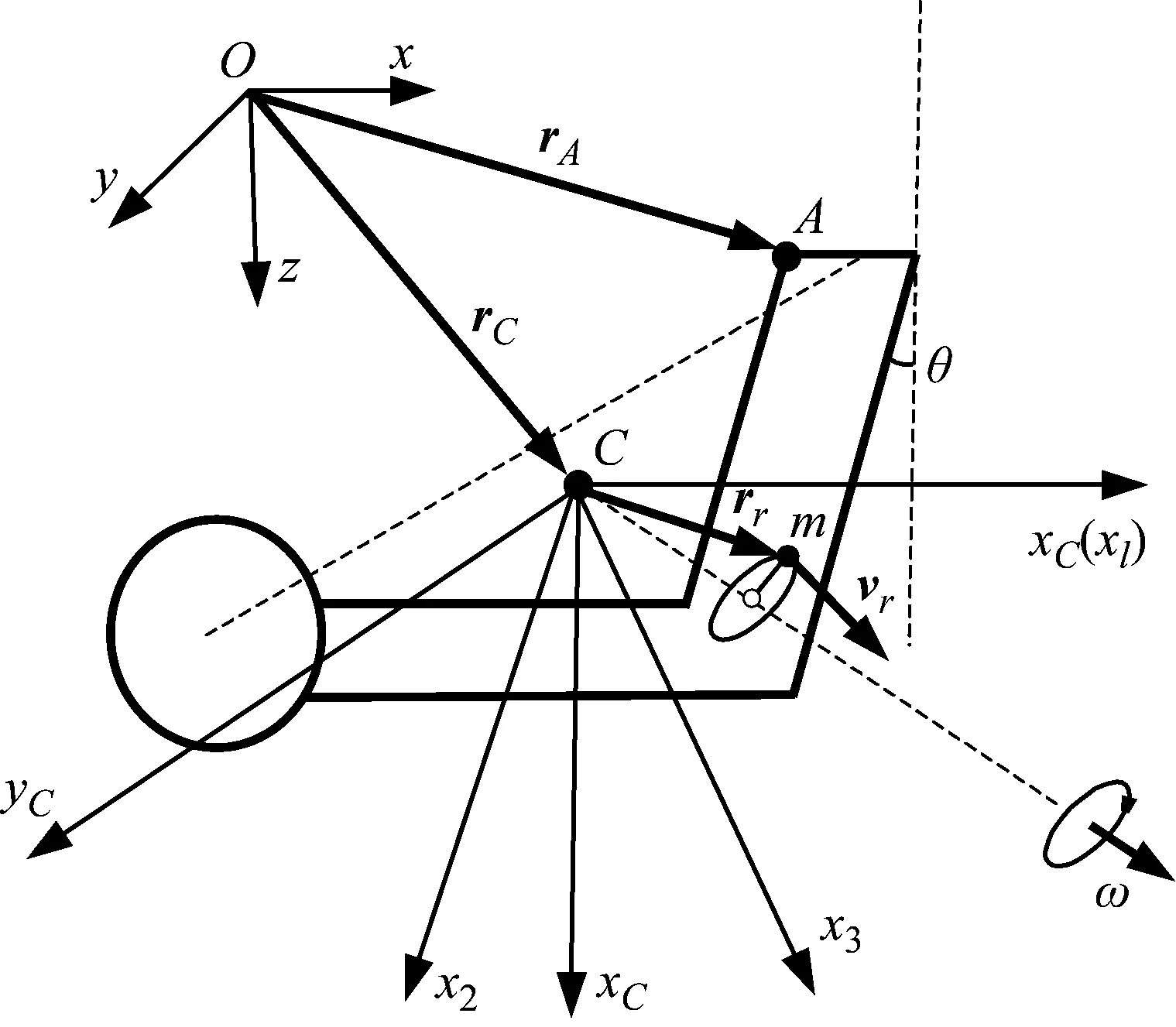
图5 锤头转动计算模型Fig.5 Hammer rotation calculation model

取平动坐标系CxCyCzC，再取与固连的正交运动坐标系Cx1x2x3，刚体的瞬时角速度为ω，根据空间运动刚体的相对运动动量矩定理，可得锤头转动方程如下

(14)

其中

在Oxyz坐标系下，锤头转动的角速度可表示为

(15)

Cx1x2x3坐标系至平动坐标系CxCyCzC的坐标转换矩阵为T

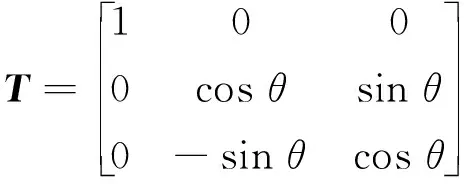
(16)

则

(17)

钢绞线对锤头A点的作用力FA对C点的力矩为

MAC=rCA×FA

(18)

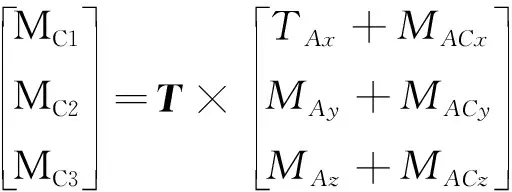
(19)

联立式(14)～(19)可得

考虑振动过程中锤头的转角较小，实际计算过程中可忽略非线性项。

2.4 防振锤阻抗计算

钢绞线抗弯刚度较小，但是由于线夹处振幅比较小，锤头的振动幅度也比较小，在防振锤固有频率范围附近振动时，采用线性理论计算的防振锤阻抗力与考虑大变形现象计算的防振锤阻抗力也相差不大，对其耗能功率影响较小。根据结构力学线性理论理论，钢绞线变形对锤头产生的作用力可表示如下

(20)

将总动力学方程表示为矩阵形式

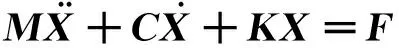
(21)

式中：M,C和K分别为FDZ防振锤的质量矩阵、阻尼矩阵和刚度矩阵；X和F分别为位移列阵和外力列阵。

其中

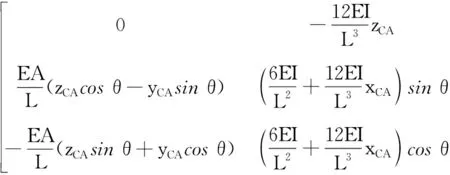
这里，Ds为系统阻尼比，xCA=xC-xA，yCA=yC-yA

zCA=zC-zA

假定防振锤线夹的位移为zO=AOejωt，其中AO为防振锤夹头的振幅，考虑稳态振动情况，则由式可解出X

X=(-Mω2+K+jωC)-1F

(22)

根据求出的X，即可求得右侧锤头钢绞线体系对夹头的作用力fR，可写成以下分量形式

(23)

分别求出两侧锤头对线夹的作用力，与线夹自身惯性力之和即为防振锤的阻抗力。

fTol=fR+fL+(0,0,mOω2AO)T

(24)

2.5 防振锤功率特性计算

防振锤振动时锤头与线夹之间的相对运动引起钢绞线的变形，这一变形过程产生钢绞线材料内的能量耗散以及线股之间的摩擦耗能。钢绞线的耗能可以通过力所做的功来计算，耗能功率可表示为以下形式

(25)

式中：fTolz为防振锤阻抗力fTol在z方向的分量，φ为fTolz与zO的相位差。

根据上述计算方法，用MATLAB语言编写了FDZ防振锤功率特性仿真程序，具体计算程序流程见图6。

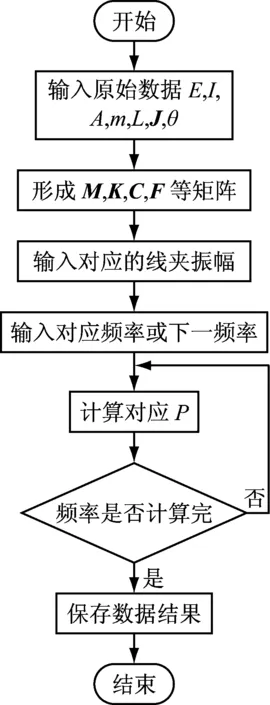
图6 防振锤功率特性计算程序流程图

Fig.6 Damper power characteristics calculation program flow chart

3 FDZ防振锤功率特性试验

本文采用激振法来测量FDZ防振锤的功率特性曲线。将防振锤直接安装到振动台上，通过测量振动台测振点处激振力和激振速度(加速度)来计算防振锤功率特性，试验系统设计见图7，现场试验照片见图8。

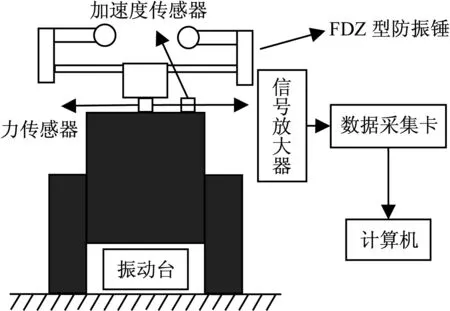
图7 试验系统设计图Fig.7 Design diagram of test system

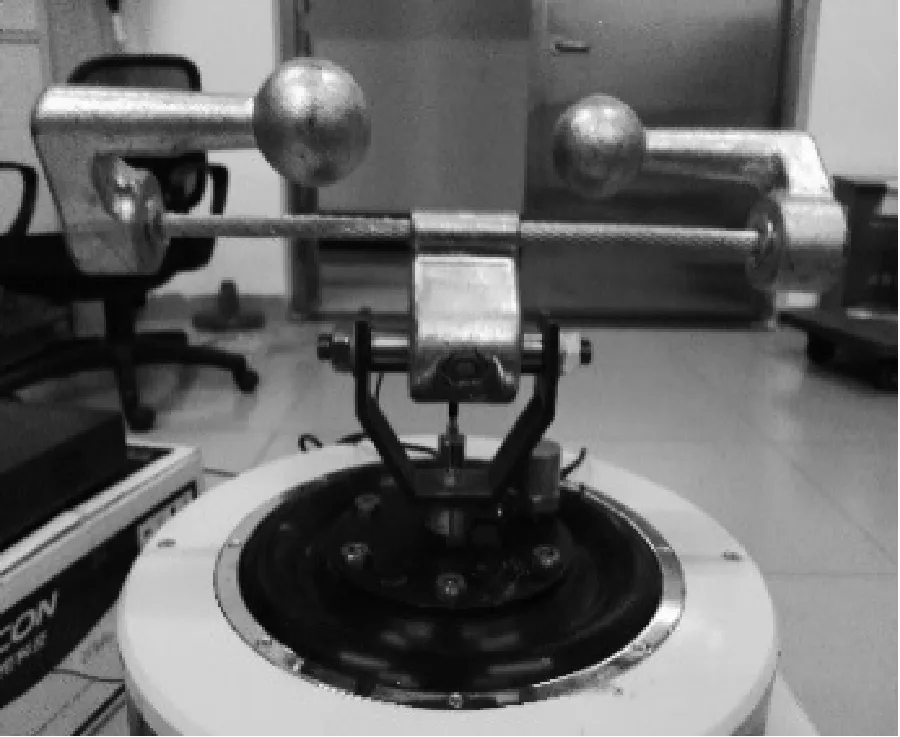
图8 现场试验照片Fig.8 Field test photos

本次试验测试的防振锤型号为FDZ3-FDZ6F。将防振锤刚性固定于振动台，对防振锤进行正弦驻频激励，频率范围5～70 Hz，频率增量为2.5 Hz。根据《防振锤技术条件和试验方法》DL/T 1099—2009，试验时保持振动速度幅值为7.5 cm/s。由力传感器获得振动台对防振锤的激振力，通过加速度传感器获得线夹加速度，所有信号处理均由软件实现。

根据采集来的试验数据，用式(26)可以计算出消耗的功率，并绘出了功率特性曲线(在4.2节给出)。

(26)

式中：P为防振锤消耗的功率；F为激振点力的测试值；a为激振点加速度的测试值；θa为激振点力和加速度的相位角。

4 算例分析

本节分别采用上述提到FDZ防振锤理论计算模型和功率特性试验，对FDZ3-FDZ6F四种防振锤型号的功率特性进行了分析，并将结果进行了比较。

4.1 防振锤物理特性参数

根据广东安恒铁塔钢构有限公司提供的防振锤设计资料，并将锤头在CAD绘出三维模型图，如图9所示，得到锤头的质心位置和转动惯量，系统阻尼比取激振试验得到的一阶阻尼比，相应物理特性参数见表1。

图9 FDZ型防振锤锤头三维模型图

Fig.9 Three-dimensional model diagram of the Hammer of FDZ-type damper

4.2 结果比较

为与试验对应，在采用本文建立的理论计算模型计算功率过程中，将夹头速度幅值设定为7.5 cm/s，并保持恒定。将理论计算和试验得到的FDZ3-FDZ6F型防振锤耗能功率绘制成频率-功率曲线，如图10～图14所示。图10～图13中峰值对应的频率见表2～表5。

从表2～表5和图10～图13可以看出，理论值功率曲线和试验功率曲线均出现了3个峰值频率。理论值功率曲线的功率峰值和峰值频率与试验数据比较接近，并且图形的走势基本一致，波峰和波谷出现的位置大致相同，整体吻合较好。但局部存在略微差异，主要原因在于：①试验外界环境对数据采集存在干扰，导致力传感器采集的数据和加速度传感器采集的数据并非标准的正弦或余弦波，在读取相应幅值和相位差时存在一定的误差；②试验时频率增量偏大，可能错过了某些特殊频率；③理论模型还不完善，忽略了一些高阶小项，并且没有考虑钢绞线的非线性。

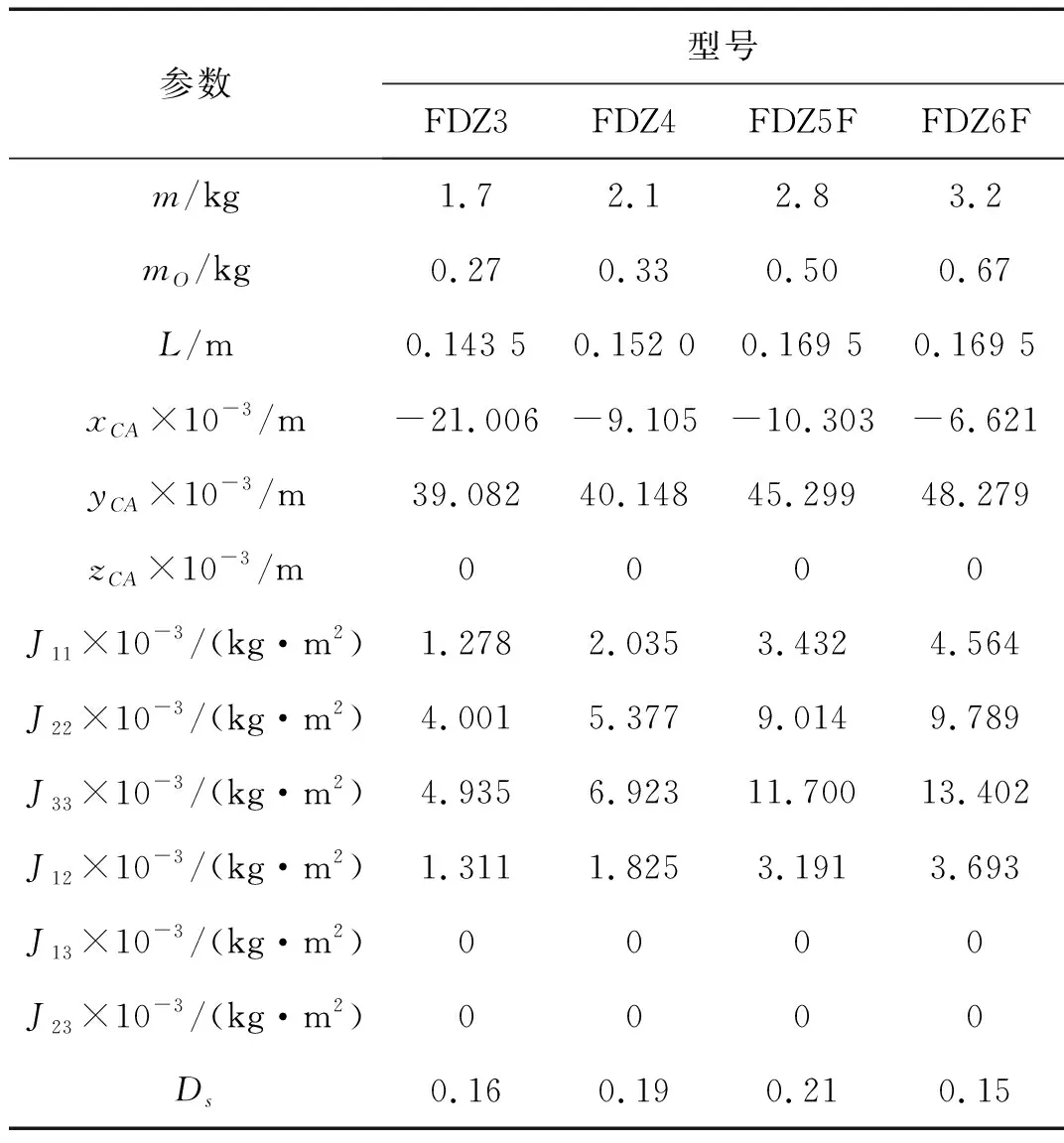
表1 物理特性参数Tab.1 Physical characteristics parameters

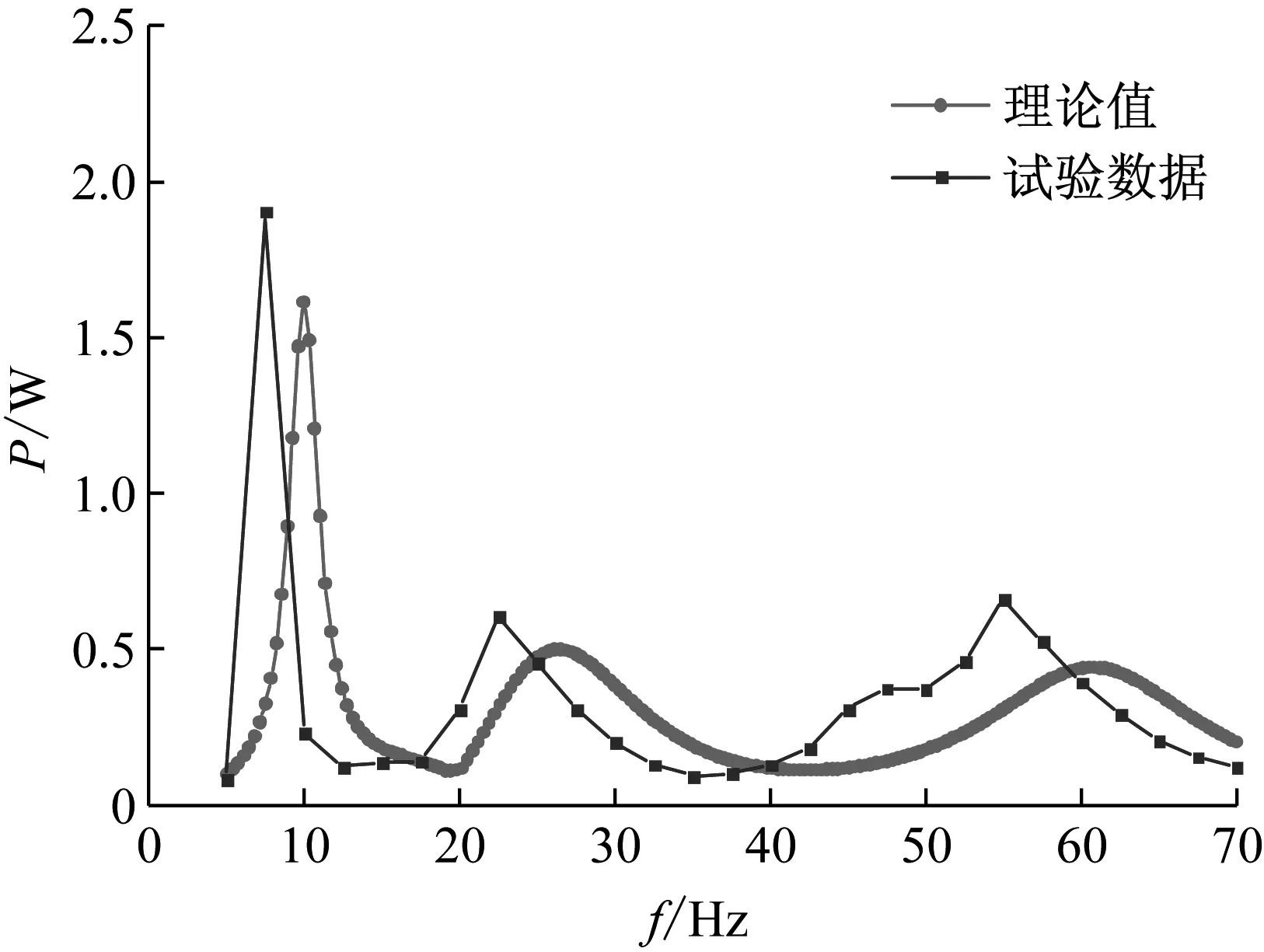
图10 FDZ3型防振锤功率特性曲线Fig.10 Power characteristic curve of FDZ3-type damper

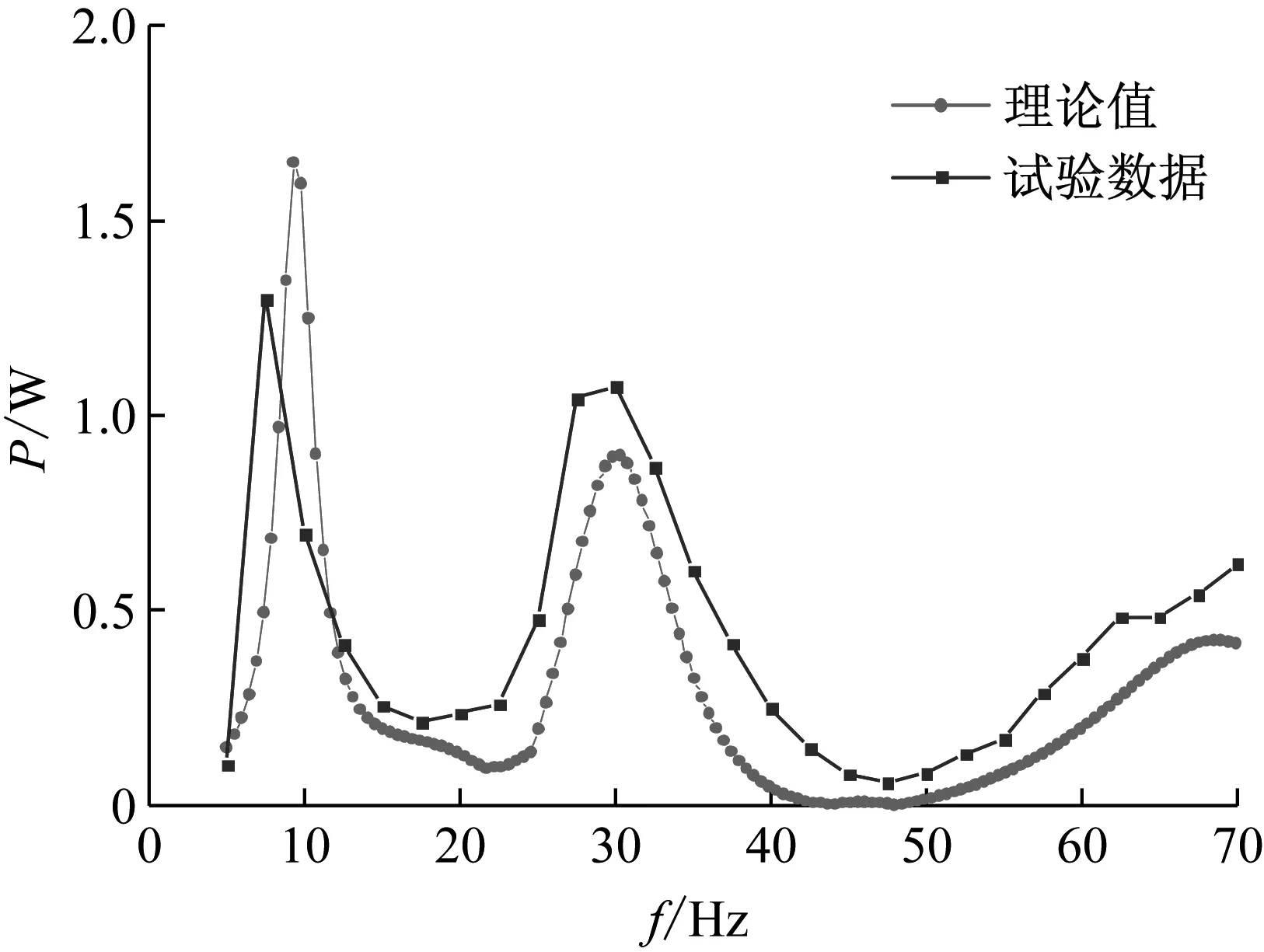
图11 FDZ4型防振锤功率特性曲线Fig.11 Power characteristic curve of FDZ4-type damper

图13 FDZ6F型防振锤功率特性曲线Fig.13 Power characteristic curve of FDZ6F-type damper表2 FDZ3型防振锤功率特性曲线峰值频率Tab.2 Peak frequencies of FDZ3-type damper power characteristic curve

频率/Hz第一个峰值第二个峰值第三个峰值理论值9.9926.4860.88试验数据7.522.555

表3 FDZ4型防振锤功率特性曲线峰值频率Tab.3 Peak frequencies of FDZ4-type damper power characteristic curve

表4 FDZ5F型防振锤功率特性曲线峰值频率Tab.4 Peak frequencies of FDZ5F-type damper power characteristic curve

5 结 论

本文根据FDZ防振锤锤头的振动特点，在FR型防振锤理论计算模型的基础上，考虑锤头的三维振动，建立了FDZ型防振锤的理论计算模型，该模型适用于各类Stockbridge型防振锤。并结合FDZ型防振激振试验，将采用理论模型计算得到的功率特性曲线和试验得到的功率特性曲线进行对比，理论值功率曲线的峰值频率与试验数据较为接近，并且图形的走势基本一致，波峰和波谷出现的位置大致相同，整体吻合较好，从而验证了模型的有效性。

表5 FDZ6F型防振锤功率特性曲线峰值频率Tab.5 Peak frequencies of FDZ6F-type damper power characteristic curve

本文建立的理论模型可以与能量平衡法[13]，有限单元法[14]和有限质点法[15]等方法结合，计算安装FDZ型防振锤的输电线路微风振动响应，改变防振锤的相关物理参数，分析这些物理参数对输电线路微风振动振幅的影响，从而对FDZ型防振锤进行优化设计。同时，运用该模型可以计算联合布置FDZ型和FR型防振锤的微风振动响应，优化传统的防振锤布置方案，达到更好的防振效果。