基于混沌特性的心音反控制方法研究

成谢锋， 佘辰俊， 李 吉

(1. 南京邮电大学 电子科学与工程学院， 南京 210003;2. 南京邮电大学 射频集成与微组装技术国家地方联合工程实验室， 南京 210003)

随着经济的不断发展，人民生活水平的日益提高，心血管疾病已然成为一类严重威胁人类身体健康的常见病。2000年以后，心血管疾病患者人数与住院治疗费用都呈现加速增长趋势，2004年至今，年均增长速度远高于GDP增速[1]。其中心悸作为心血管疾病的症状之一，是一种主观上患者感觉心脏跳动快速、不整或搏动有力，客观上可见心跳频率过快、过缓或不齐等心率和心律变化的心血管疾病。心脏作为人体最为重要和复杂的非线性动力系统之一，自从发现心脏是一个混沌系统以来，人们对其进行了大量基于混沌理论的心脏动力学研究。心音信号作为心脏舒张和收缩的复杂机械运动过程中心肌、血液、心血管及瓣膜等所产生的复合音，能很好的反映心脏各个部分如心房、心室、心血管及各个瓣膜的功能状态，且蕴含了大量的生理与心脏早期病变的病理信息[2]。国内外学者对心音信号混沌性进行了探索性的研究，并取得了一些有价值的结论。Grebogic等[3]提出了混沌控制理论可以控制心率失常，随后Garfinkel 等[4-5]运用了正比扰动反馈的控制方法(PPF)所产生基于混沌理论的电刺激信号去激励心律不齐的兔子心脏使得心脏转为规律跳动更加证明了Grebogic的观点。并将此控制技术与起搏器结合使用，达到了不错的防止心室纤颤的效果。丁晓蓉等[6]从混沌理论的角度对心音信号进行结合小波包分析的混沌动力学分析，在本质上深入地认识了心音信号的内在规律，得出正常、异常心音的混沌特性存在显著差异的结论，为心脏早期病变的计算机辅助诊断提出了一条新路径[7-8]。成谢锋等[9]从运动与年龄角度对心音混沌特性规律做出相关研究，得出心音的混沌特征参数受运动及年龄影响形成的变化规律。孙丽莎等[10]基于最大Lyapunov指数的心音信号混沌特性分析，得出心音信号的确存在混沌现象，且正常(健康)心音信号S1、S2阶段的混沌性都要明显强于病理心音信号。我们认为，既然可以利用基于混沌理论的电刺激信号去激励心律不齐的心脏使得心脏转为规律跳动，那么也可以考虑用基于混沌控制理论的振动信号去帮助心律不齐的亚健康人群。常见有心脏不适患者会对胸腔外部进行敲打与按摩，以达到一定程度上缓解心血管疾病不舒的目的。目前市面上有多种敲打式按摩棒与电动按摩器、按摩椅，但其理疗方式不具有针对性，即敲打与按摩的频率与强度是预先固定的，不能产生有针对性的混沌振动效果。

本文拟从混沌反控制角度对心音信号进行处理，结合混沌精确跟踪控制、跟踪微分器原理、PID控制理论和模糊控制理念，提出一种适用于进行心音混沌反控制的控制方法。该方法可使得病理心音信号实时精确的跟踪正常心音信号的轨迹，且其混沌特性得到明显增强，以产生针对性的混沌振动信号。仿真实验表明，该方法可使得心率和心律异常变化的心音信号跟踪上正常心音，达到反控制的效果。同时用本文提出的方法开发智能按摩设备，能够产生出有针对性的混沌振动效果，以达到更加理想的医疗辅助理疗效果。

1 心音混沌反控制方法的设计原则与标准

1.1 心音混沌反控制方法的设计原则

本文提出的心音混沌反控制方法旨在利用心音信号本身所具有的混沌特性并结合混沌反控制的相关理论，对心音信号进行非线性处理，实现心音信号的混沌反控制。为了使设计的心音混沌反控制方法能够很好地适应心音信号的不确定性，即心音信号无法用数学公式进行精确数学化表达，本文将模糊理论用于心音信号的控制过程。为了降低此控制方法对于输入心音质量的要求，即省略心音信号预处理过程。本文将非线性微分-跟踪器用于对输入心音信号进行滤波和求取一阶跟踪微分，以求取模糊控制所需的ec输入量。

综上所述，本文在设计心音混沌反控制方法时力求做到以下原则：① 针对性，是指针对心音的混沌特性，特别是针对正常与异常心音的混沌性差异去实现反控制;② 实时性，是指能在自然环境下对心音信号进行反控制处理，不需要进行去噪、分段等预处理;③ 普适性，是指能够适用于多种与多类不同的病理心音信号；④ 实用性，可用于开发心血管疾病的相关医疗辅助理疗设备，具有一定的实用价值。

1.2 心音混沌反控制方法的设计标准

本文提出的心音混沌反控制方法的设计标准为： ① 鲁棒性，心音混沌反控制方法能够很好地消除输入的心音信号噪声参数的扰动影响并具有较好的方法稳定性;② 精确性，从定性角度体现在控制后的病理信号能够很好的对正常心音信号进行轨迹跟踪且两者的轨迹误差趋近于0，从定量角度体现于反控制后的病理信号的混沌特性得到增强;③ 快速性，使得输入的病理心音信号能够快速地完成整个轨迹跟踪过程。

2 心音混沌反控制方法设计原理

按照上述心音混沌反控制方法的设计原则与标准，本文提出了结合TD与Fuzzy-PID控制理论的心音混沌反控制方法，方法框图如图1所示。其中，为了满足方法设计实时性的原则与方法设计标准，本文根据TD的特性用TD1来安排理想的控制过渡过程和对输入的正常心音信号进行滤波与微分；TD2来尽快恢复反馈信号Y(t)并进行滤波和给出其跟踪微分信号。

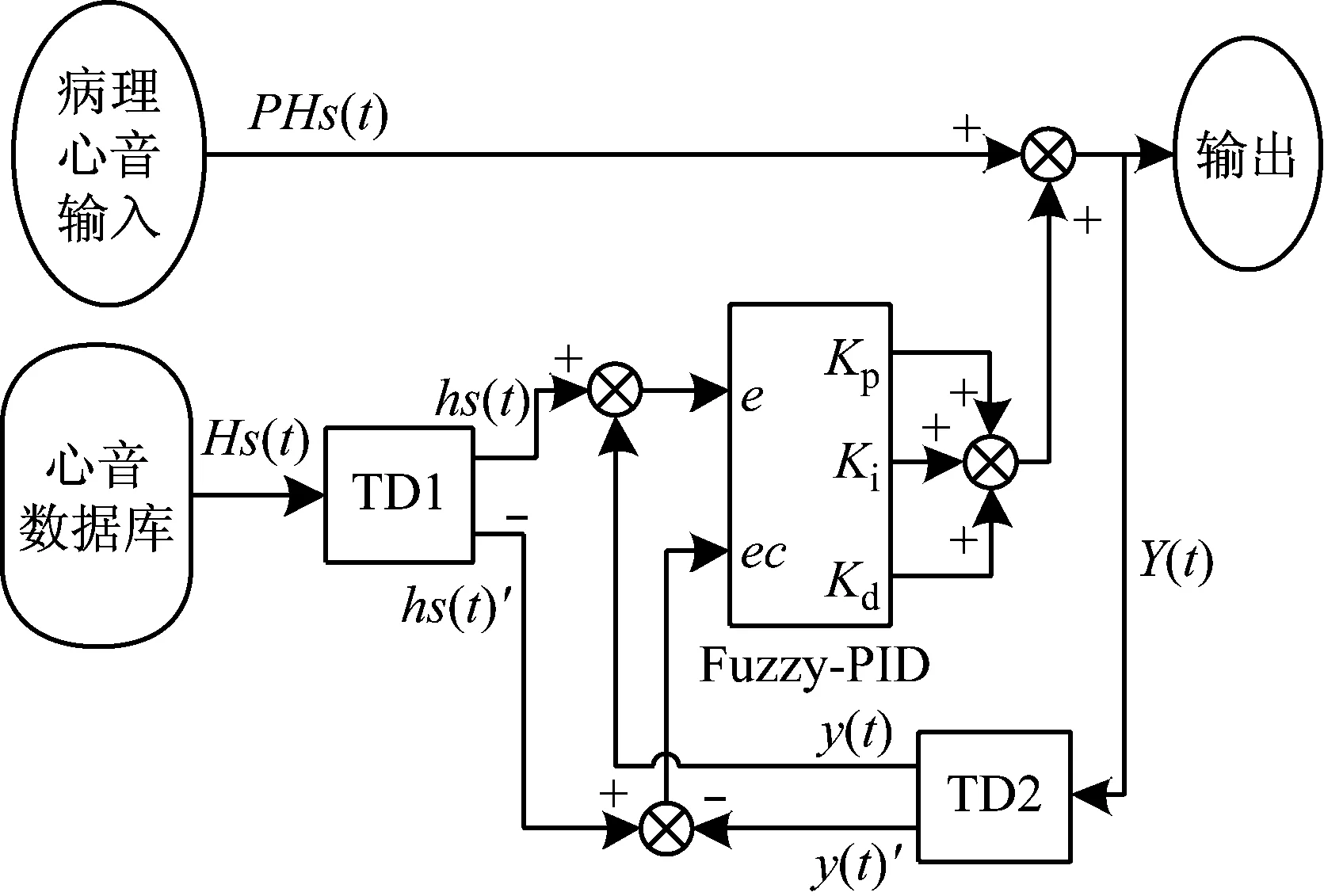
图1 心音混沌反控制方法框图Fig.1 Block diagram of chaos anti-control method of heart sound

2.1 跟踪微分器(TD1和TD2)

跟踪微分器是一种依据输入信号输出其跟踪信号和跟踪信号近似微分信号的动态方法。其中由跟踪-微分器得到的近似微分信号为输入信号的广义导数的一种光滑逼近[11-12]。为了贴合上述提出的方法针对性原则，本文所用的TD1的输入信号为正常心音数据库读取的正常心音信号Hs(t)，经TD1处理后得到Hs(t)的跟踪信号hs(t)与hs(t)的近似微分信号hs(t)′。则针对Hs(t)输入的二阶跟踪-微分器的方程为

(1)

为了避免原点附近的颤振，将符号函数sign改为饱和函数sat得到有效的跟踪-微分器形式为

(2)

考虑到数据库输入的正常心音信号是经过A/D转换后得到的，因此本文选用微分跟踪器的二阶离散形式。微分跟踪器的离散形式为

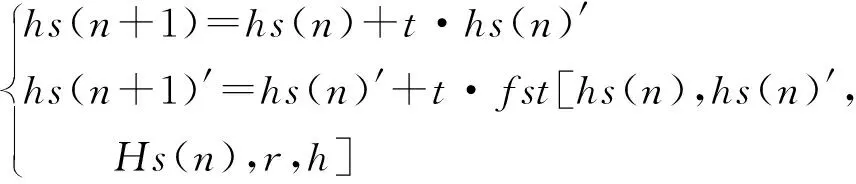
(3)

式中：Hs(n)为正常数据库读取的心音信号；Hs(n)为读取心音信号；hs(n)为跟踪信号；hs(n)′为hs(n)的微分信号；r为跟踪速度因子，可变参数，r在积分条件下理论上应该取到极限，但是离散形式下r取为有限值；h为滤波因子，可变参数，影响跟踪微分器的微分和跟踪效果，通过调整h值可以求得合适的参数δ′，得到适合心音的滤波器参数即跟踪微分器参数；t为跟踪步长。fst函数的运算过程为

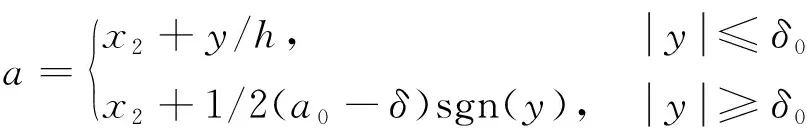
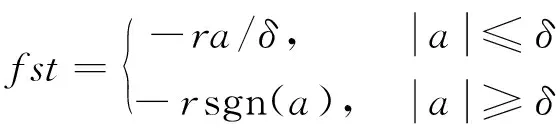
(4)

式中：v为输入信号Hs(n)，参数r越大，hs(n)越能更好的跟踪输入的心音信号Hs(n)，但当Hs(n)中混有噪声信号时，hs(n)中的噪声会被放大。为了更好的滤除所含噪声，需要选取合适滤波因子h才能获得很好的滤波效果，但h越大，hs(n)信号与Hs(n)的相位偏移会越大。针对心音信号的特性，经反复调测，r=2 000，h=0.001,t=0.001 s时，TD1获得最佳处理效果。

TD2原理同TD1，用来对反馈信号Y(t)进行滤波和快速恢复，并输出Y(t)的跟踪信号y(t)与y(t)的近似微分信号y(t)′。

2.2 Fuzzy-PID控制方法

PID控制是一种已经广泛运用于工业生产的且较为成熟的控制技术，PID控制量u(t)主要由输入和被调量的误差及微分线性组合来产生，控制规律

(5)

式中：e(t)=v(t)-y(t),v(t)为输入量，y(t)为被调量；通过对比例系数kp、积分系数ki、微分系数kd的调整，得出适用于被控对象的控制量以达到满意的结果。虽然PID控制简单易行，但其只能得到固定的三个控制参数，对于无法用数学模型精确表示的心音信号，由于控制参数的实时变化性，PID控制达不到精确控制的效果且抗干扰能力也较差[13]。

心音信号是一种非平稳、非线性的不确定信号且不同主体的心音信号存在差异性，所以无法找到精确的数学表达式来抽象表示出心音信号。为了适应心音信号不确定性的特点和满足心音信号作为输入的针对性设计原则，本文将PID控制与模糊理论相结合构成Fuzzy-PID控制方法，此方法在运行过程中通过不断检测误差e和误差变化率ec与PID三个参数之间的模糊关系，根据已经确定的模糊控制规则来对三个参数进行在线修改，以满足不同e和ec时对控制参数的不同要求，从而使被控的心音信号有良好的动、静态性能。由于仅利用了心音信号的I/O数据及经过处理得到的反馈数据，且结合了PID控制的优点，因此该方法具有更好的智能性和适应性。

Fuzzy-PID控制主要分为三步：① 计算当前两路输入心音信号的误差e和其两者的误差变化率ec；② 利用既定的模糊规则进行模糊推理；③ 查询模糊矩阵表进行参数调整。

Fuzzy-PID设计的核心是在总结专家的技术知识和实际操作经验的基础上，建立合适的模糊规则表，得到针对kp、ki、kd三个参数分别整定的模糊控制表[14-19]。 参数kp、ki、kd的模糊控制表如表1、2、3所示。

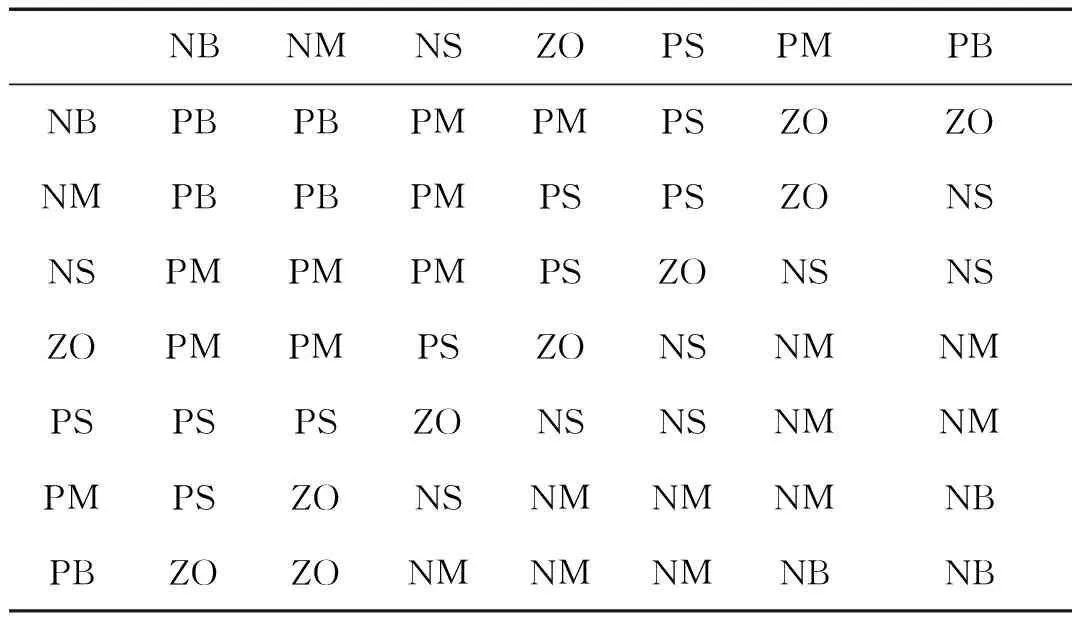
表1 kp的模糊控制规则表Tab.1 kp Fuzzy control ruleTable

将方法误差e和误差变化率ec的变化范围定义为模糊集上的论域，针对心音信号的特点，设定论域为{-6,6}，即：e,ec={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。其模糊子集为e,ec={NB,NM,NS,ZO,PS,PM,PB}，子集中元素分别代表负大、负中、负小、零、正小、正中、正大。

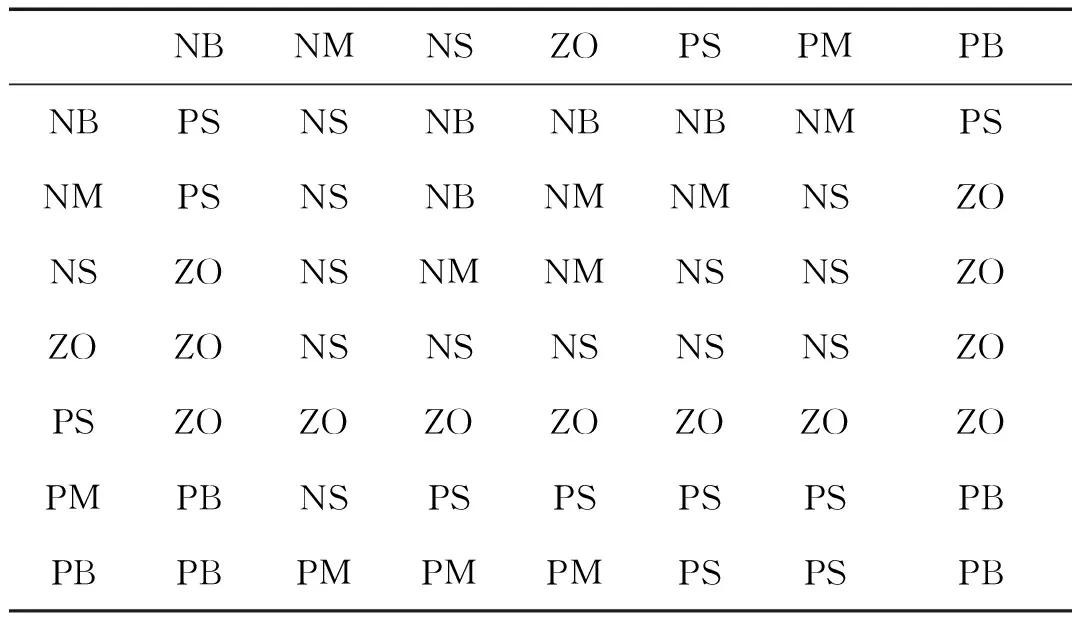
表2 ki的模糊控制规则表Tab.2 ki Fuzzy control ruleTable

表3 kd的模糊规表Tab.3 kd Fuzzy control ruleTable

kp、ki、kd的论域分别为[-0.3,0.3]，[-0.3,0.3]，[-3,3]，根据论域的灵敏度、覆盖程度、稳定性和鲁棒性等原则，所有的模糊语言变量的语言值都以三角形为隶属度曲线。最后将获得的修正参数代入下式计算

(6)

2.3 心音信号混沌反控制方法工作过程

在图1所示心音信号混沌反控制方法中，本文将正常心音数据库读取的正常心音信号Hs(t)作为TD1的输入信号，经过TD1处理后得到其跟踪信号hs(t)和hs(t)的近似微分信号hs(t)′，同理，将实时采集的病理心音信号PHs(t)作为TD2的输入信号，然后依据得到的TD1、TD2输出信号求得初始时刻t0的信号误差e与信号误差变化率ec，并作为Fuzzy-PID控制模块的输入。Fuzzy-PID控制模块依据预设的模糊规则与模糊矩阵表进行模糊推理、参数调整，并输出kp、ki、kd三个控制参数。

由上述三个控制参数线性组合得到控制律U，作用于输入的病理心音信号PHs(t)，使得病理心音信号跟踪初始时刻t0正常心音信号的轨迹。最后，依据反馈控制原理，完成心音信号长度为T的心音混沌反控制过程，得到控制后的病理心音信号作为输出。具体流程图如图2所示。

图2 心音信号混沌反控制方法工作流程图Fig.2 Flow chart of chaotic anti-control method of heart sound signal

3 心音混沌反控制应用实例

3.1 实例1

本文使用课题组自研肩带式心音采集装置进行实验所需的心音信号采集(已申请中国发明专利)，采样频率fs为11 025 Hz。基于MATLAB/Sumilink平台进行仿真，其中仿真区间步长T0为0.01。

3.1.1 跟踪微分器滤波效果实验

在输入的心音信号Hs(t)上附加10 dB的高斯白噪声得到混合信号Hs1(t)，将混合信号Hs1(t)作为TD的输入信号，Hs1(t)如图3(a)所示。得到Hs1(t)的跟踪信号hs1(t)如图3(b)中第二幅图和hs1(t)的近似微分信号hs1(t)′如图3(b) 中第三幅图所示。图3说明了TD对于心音信号具有很好的适应性和滤波效果，不需要对输入心音进行预处理，能满足设计心音信号混沌反控制方法的实时性原则。

3.1.2 心音混沌反控制效果实验

本实验选择的一组正常与病理心音信号波形如图4(a)、(b)所示。将它们输入基于MATLAB/Sumilink平台的心音混沌反控制方法框图中，进行心音信号的混沌反控制实验。混沌反控制后的病理心音信号跟踪校正波形图如图5所示。其跟踪误差曲线如图6所示。

(a) 原始心音信号

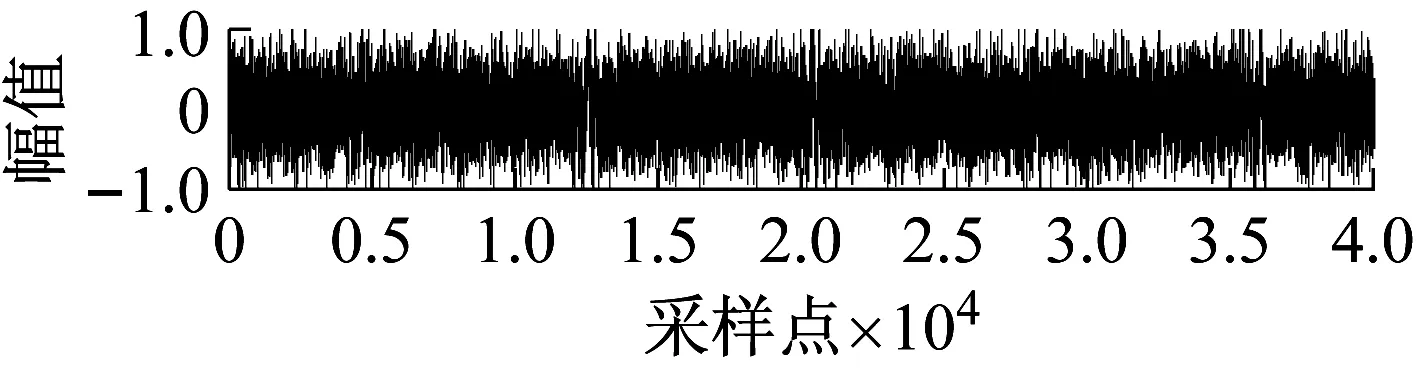
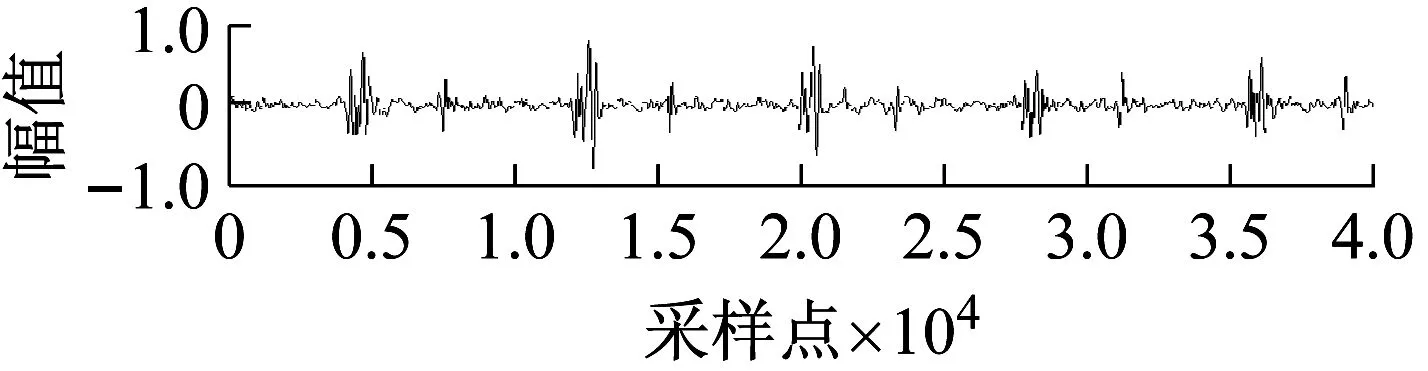
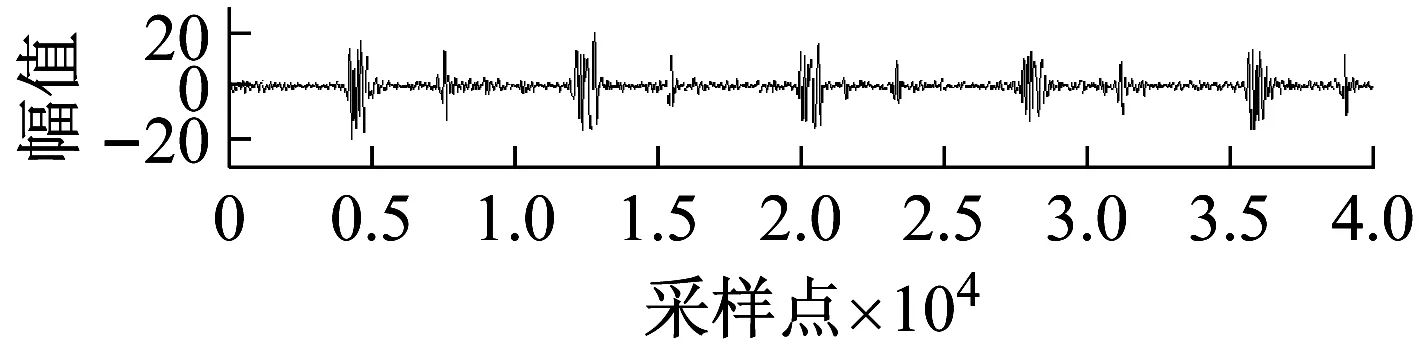
(b) 微分跟踪器滤波效果图3 原始心音信号及微分跟踪器滤波效果图Fig.3 Differential tracker filter effect chart and original heart sound signal

(a) 输入的正常心音信号Hs(t)(b) 输入的病理心音信号PHs(t)

图4 输入的正常与病理心音信号波形图

Fig.4 Enter the normal and pathological heart sound signal waveforms

图5 经心音混沌反控制后的跟踪校正波形图Fig.5 The tracking correction waveform after anti-control of the heart sound chaos

3.1.3 心音混沌反控制效果实验

本实验选择的一组正常与病理心音信号波形如图4(a)、(b)所示。将它们输入基于MATLAB/Sumilink平台的心音混沌反控制方法框图中，进行心音信号的混沌反控制实验。混沌反控制后的病理心音信号跟踪校正波形图如图5所示。其跟踪误差曲线如图6所示。

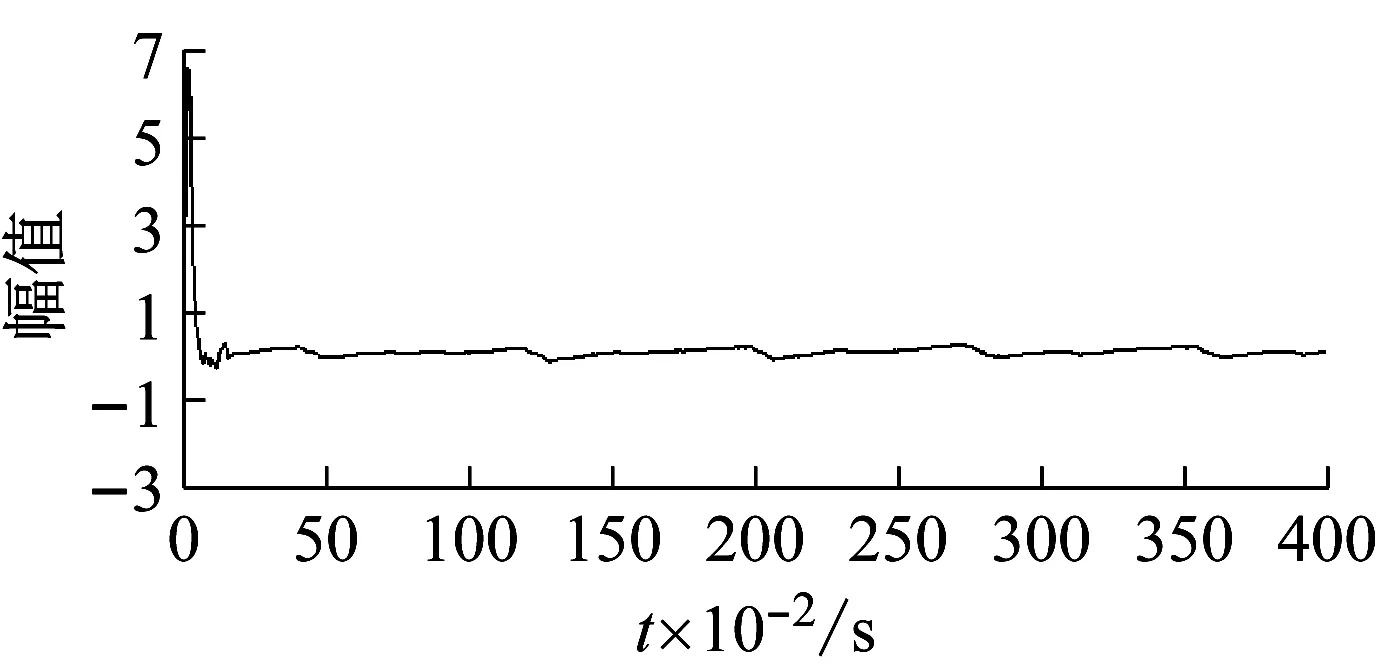
图6 病理心音跟踪的误差曲线图Fig.6 Pathological heart sound tracking error curve

从图5可见，病理心音波形在跟踪步长点数为25处开始跟踪上输入的正常心音波形，因为区间步长为0.01，大约需0.25 s就可将病理心音调整为正常心音。在图6中，跟踪误差曲线在0.25 s后开始趋近于0，且跟踪误差在0附近有微小浮动，浮动区间为[0, 0.2]。可见本文提出的方法跟踪快速且精度较高。

3.2 实例2

心脏早搏是一种最为常见的异位起搏的心律失常疾病，可偶发或频发，可以不规则或规则的在每一个或每数个正常搏动后发生，形成二联律或联律性过早搏动。常见于冠心病、风湿性心脏病、高血压性心脏病、心肌病等器质性心脏病患者，也可见于正常人。本文又选取了一个早搏患者的心音进行验证。心脏早搏患者在正常时的心音信号与发生早搏时的心音信号分别如图7(a)、(b)所示。坐标表示同图4。早搏心音信号经混沌反控制后的跟踪校正波形图如图8所示。其跟踪误差曲线如图9所示。

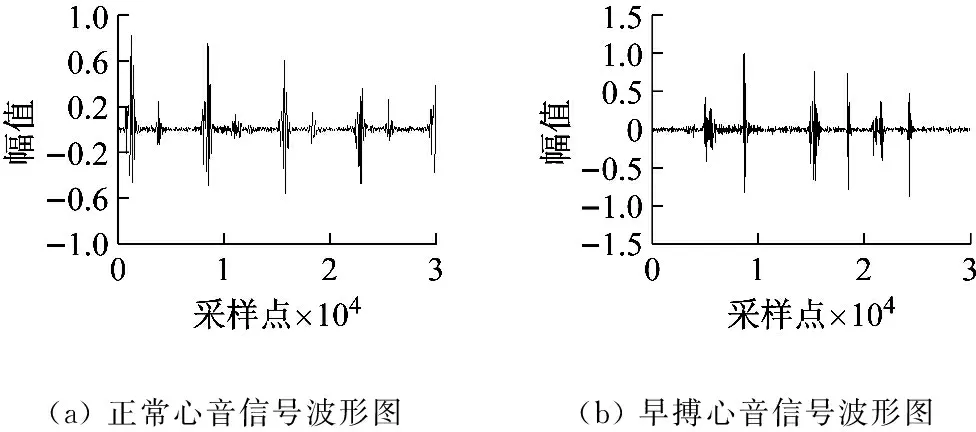
(a) 正常心音信号波形图(b) 早搏心音信号波形图

图7 同一心脏早搏患者的正常心音信号与早搏心音信号波形图

Fig.7 Normal heart sound signal and premature heart sound signal waveform in the same patient with premature beat

图8 经心音混沌反控制后的跟踪校正波形图Fig.8 The tracking correction waveform after anti-control of the heart sound chaos

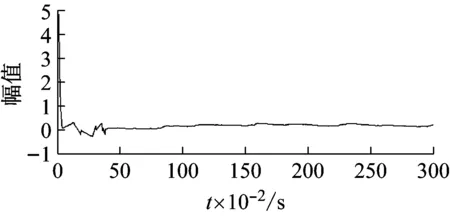
图9 跟踪误差曲线图Fig.9 Pathological heart sound tracking error curve

对实例2中的图8、图9进行分析可得，早搏心音信号约在0.34 s处开始对正常心音信号波形进行轨迹跟踪且跟踪误差趋近于0，跟踪误差浮动区间为[0,0.15]。上述实验结果表明，本文提出的心音混沌反控制方法对于早搏心音信号也具有跟踪速度快，控制精度高、鲁棒性较好的特点。

3.3 心音混沌反控制结果分析

上述实验结果定性地表明了心音混沌反控制方法的合理性与可行性，本小节将依据相关的混沌理论，定量分析控制前后病理心音的混沌特性变化情况。

最大Lyapunov指数是一种定量描述混沌方法相空间相邻轨道之间平均指数发散性与收敛性的参数。通过计算方法的最大Lyapunov指数可以来推断方法是否存在混沌，其中若该指数为正值则意味着方法混沌且该指数的大小与方法混沌的强弱相关，越大说明方法混沌性越强。Lyapunov指数作为已广泛应用于方法混沌性证明的理论，已成为一种重要的非线性信号混沌分析的方法之一。

分别截取一段实例2中所输入的正常心音信号与混沌反控制前、后的早搏心音信号，采用互信息法求它们的延迟时间τ，和用Cao法求它们的嵌入维数m，其中m的范围为1～20。将求得的τ与m作为小数据量法分析最大Lyapunov指数。其中,正常心音的最大Lyapunov指数如图10(a)所示，控制前后的早搏心音最大Lyapunov指数分别如图10(b)、(c)所示。正常心音与控制前后早搏心音的τ、m、最大Lyapunov指数对比结果如表4所示。

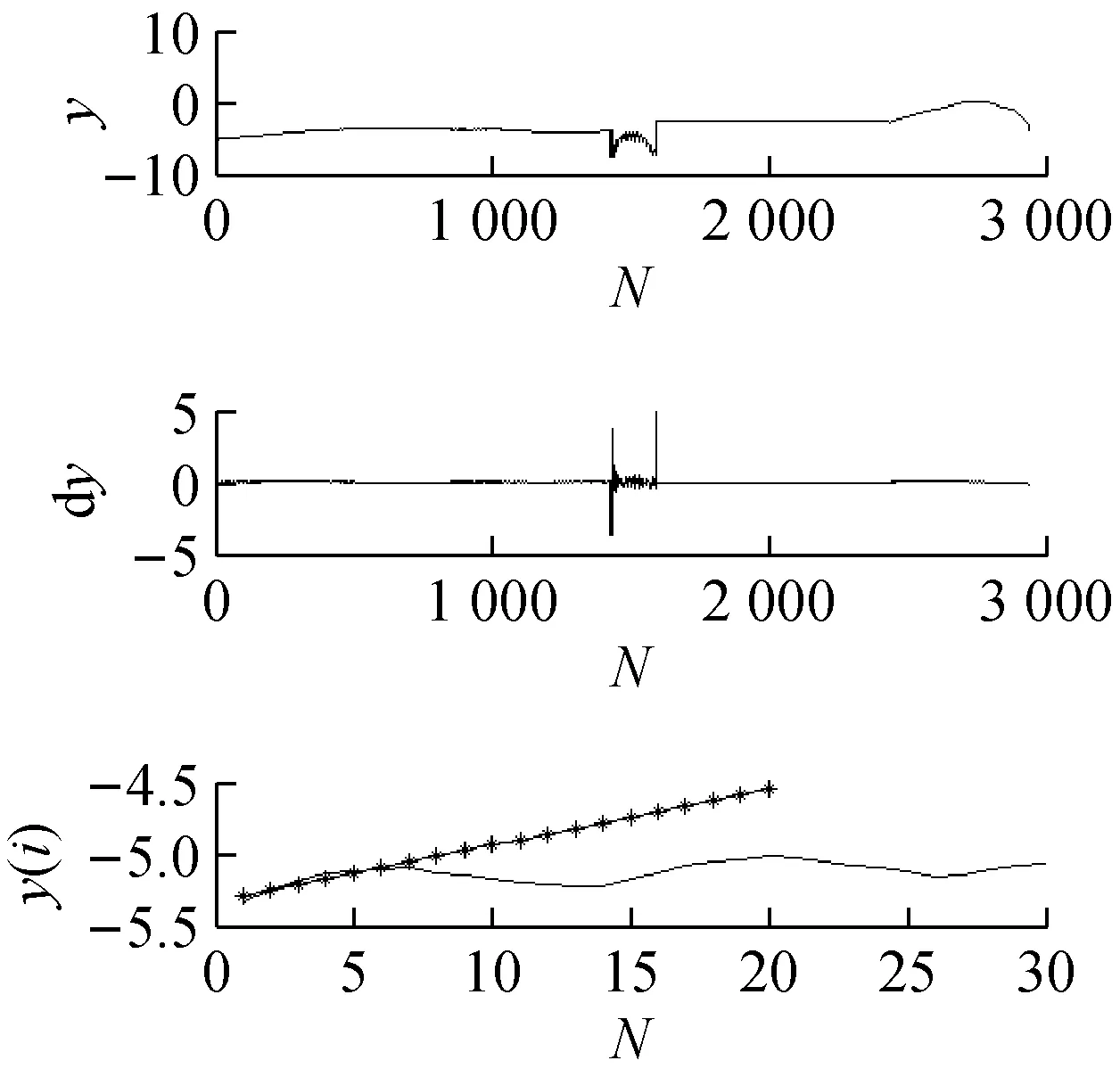
(a) 正常心音的最大Lyapunov指数

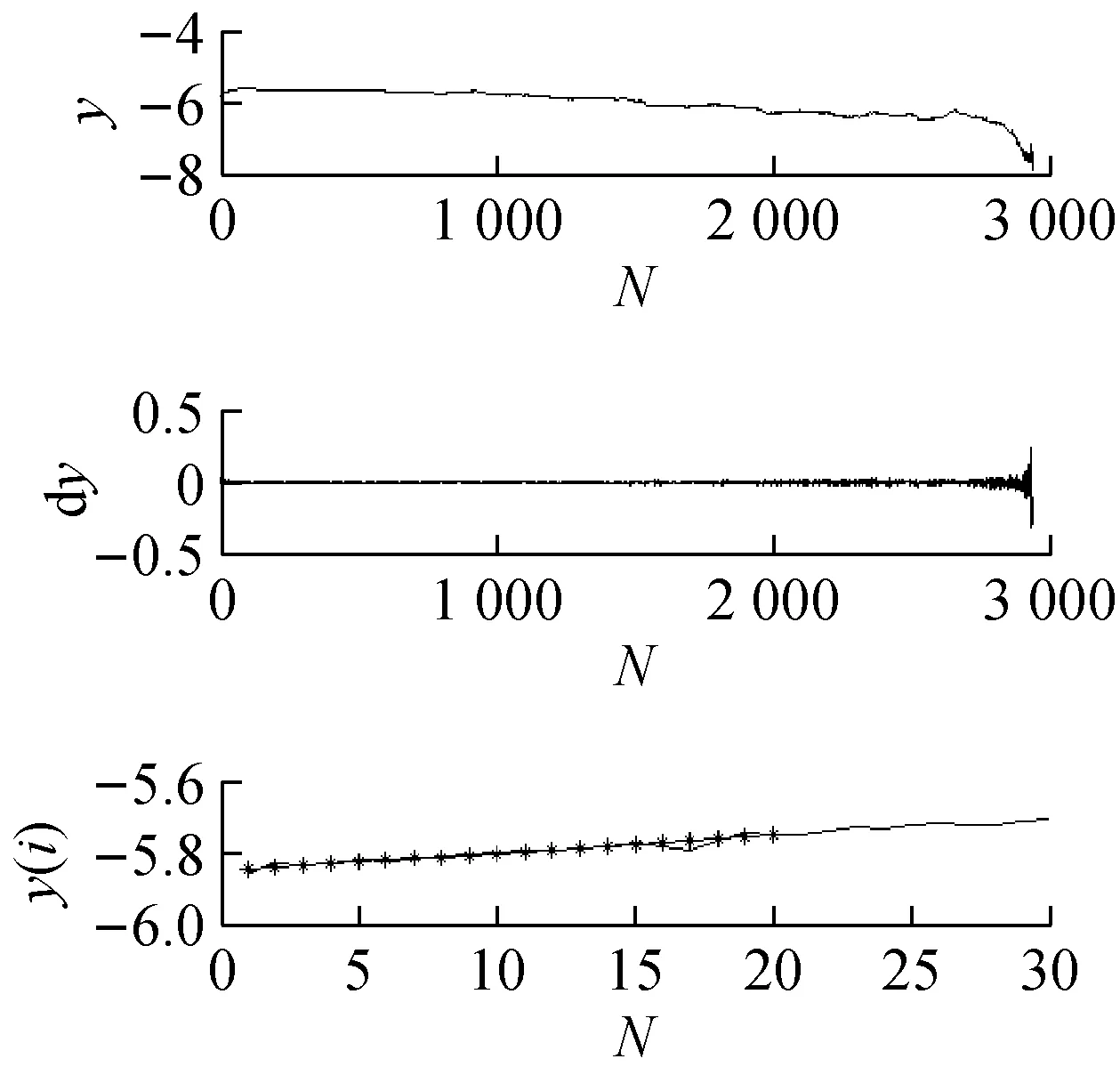
(b) 控制前的早搏心音最大Lyapuno指数

(c) 控制后的早搏心音最大Lyapuno指数图10 正常心音信号与控制前后的早搏心音最大Lyapunov指数图Fig.10 The largest Lyapunov exponent of Normal heart sound signal and the premature heart sounds before and after control表4 正常心音与控制前后早搏心音的τ、m、最大 Lyapunov指数对比表

Tab.4Normalheartsoundsandcontrolbeforeandaftertheheartbeatτ,m,thelargestLyapunovindexcomparison
Table

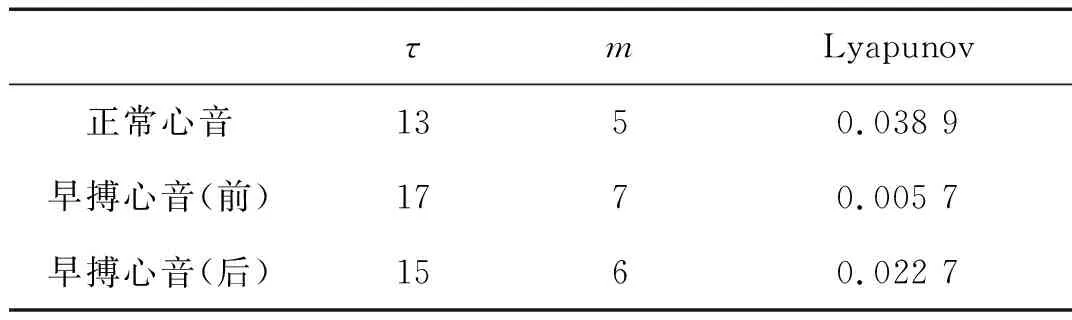
τmLyapunov正常心音1350.038 9早搏心音(前)1770.005 7早搏心音(后)1560.022 7

通过对实验2结果的定量分析，可见控制后的早搏心音信号的混沌性得到显著增强。这进一步表明本文所提出的心音混沌反控制方法具有合理性与可行性。

4 结 论

(1) 本文提出了心音混沌反控制方法的设计原则与标准，并依据此原则和标准，实现了一种跟踪速度快、误差小、鲁棒性好、且具有一定实用价值的心音混沌反控制方法。

(2) 从定性与定量两个方面对心音混沌反控制方法的实验结果进行了分析，实验结果表明，本文提出的心音混沌反控制方法完全达到预期的设计要求。

将本文提出的心音混沌反控制方法用于相关心血管疾病的智能辅助理疗设备开发，将是本课题的后续工作。