基于火药燃气压力空间变化的火炮发射动力学研究

于情波， 杨国来， 葛建立， 孙全兆， 萧 辉

(南京理工大学 机械工程学院， 南京 210094)

火炮射击过程中弹丸与身管内壁的接触碰撞作用以及高压火药燃气对身管内壁的冲刷作用，使得身管产生一定的弹性振动，弹丸出炮口时身管炮口处的振动对弹丸初始运动姿态具有直接的影响[1-2]，从而影响火炮射击精度。对于身管振动的研究，姜沐等[3]将身管简化为一悬臂梁，弹丸的作用简化为一加速移动的载荷，建立了身管的运动方程，求得了级数形式的解析解。刘宁等[4]把身管简化成等截面悬臂梁，根据Bernoulli-Euler初等梁理论建立了身管振动方程，用模态分析法求解了身管振动方程。苏忠亭等[5]将身管等效为变截面悬臂梁，并计算分析了内弹道时期弹丸移动对身管振动特性的影响。文献[6]同样研究了移动质量作用下悬臂梁的振动特性。该研究方法对身管实际结构过于简化，并且忽略了火药燃气的冲击作用,计算得到的解析解与实际情况误差较大。

有限元分析方法作为火炮发射动力学研究的常用方法，能够反映火炮的模态特征，应力，应变的分布情况，可以模拟弹丸在内弹道时期的运动形态以及火炮零部件的动力学响应。葛建立等[7]考虑了弹丸弹带、前定心部与膛壁的碰撞及膛线对弹丸的扭转作用，分别仿真计算了火炮在有无膛线的情况下弹丸在膛内的运动过程。许耀峰等[8]建立某大口径火炮线膛身管与制导炮弹耦合动力学有限元模型，数值计算了膛线形式，膛线深度对弹炮动力学响应的影响。吴会民等[9]采用数值方法对弹丸身管耦合作用下系统动力响应进行了计算，得到了身管扭转动力响应和横向动力响应的基本规律。在现有的大部分针对弹丸在膛内的运动响应及身管振动特性的研究中，仅限于弹丸膛内响应规律研究，忽略了直接作用于身管内壁的火药燃气压力对身管动态响应的影响。火药燃气压力属于强冲击载荷，其压力值和作用于身管内壁的分布情况均与时间有关，并且具有阶跃型脉冲动态效果，是激发身管振动不可忽视的因素。可学为等[10]研究了火药燃气压力对身管振动的激励作用，利用 ABAQUS 软件建立身管的三维有限元模型，将火药燃气压力作用区域沿身管轴向离散成一系列较小的作用区域，并将对应的压力曲线施加到身管各个离散区域。火药燃气压力根据弹丸的运动位置实时作用于弹后身管内壁，利用此方法对身管施加燃气压力，不能准确模拟实际压力场二维分布情况，并且没考虑弹丸与身管的耦合作用，求得的结果与实际情况存在较大差别。

另外，关于身管强度失效的报道屡见不鲜，但现有关于身管强度分析的文献少之又少。数值模拟实现火炮身管实际受载环境，得到身管强度动态变化情况，对身管强度失效分析具有重要的参考价值。部分文献对身管内膛损伤机理进行了研究分析，曾志银等[11]研究了弹丸装填不到位造成的冲击加载对身管材料动态性能的效应，分析了导致阳线起始段局部双侧棱边断裂损伤的可能原因。刘广生等[12]对某型火炮多发射击工况下内膛损伤破坏过程进行了数值模拟计算，分析了弹带挤进内膛过程中身管内壁材料性能随射弹发数变化的规律。文献中数值计算了身管内膛在火炮射击中的动力学响应，但均忽略了火药燃气压力的影响，不能真实描述身管实际动力学响应。曾志银等[13]运用 ANSYS 有限元分析软件的APDL语言，计算分析身管在径向受载下的动力学响应，通过载荷上升时间确定身管截面承受的阶跃型脉冲，并没有严格按照实时弹丸轴向运动位置定义燃气压力二维分布，不能准确模拟实际射击环境下身管受载情况。

考虑到高压火药燃气压力二维分布特性对身管动力学响应的影响，本文在现有的火炮发射动力学研究的基础上，建立了弹丸与身管耦合非线性动力学模型。借助有限元软件提供的用户自定义子程序，实现了弹丸膛内运动与经典内弹道火药燃烧相互关联的动力学过程，基于身管振动理论，数值计算过程计及了火药燃气压力对身管振动的激励作用，实现了膛内火药燃气压力随弹丸运动而动态变化的二维分布情况。结合实弹射击实验，有效验证了建立的数值模型的正确性，对火炮发射过程的数值模拟提供了更接近实际的力学边界条件，更真实地再现了身管动力学响应。

1 力学模型

借鉴欧拉-伯努利梁模型[14]，身管可以简化为一端固定另一端自由的变截面悬臂梁。身管在整个内弹道过程中受到火药燃气膨胀波以及与弹丸接触碰撞的作用，简易力学模型如图1所示。图中M为弹丸的质量，Fcont为不计惯性效应时弹丸膛内运动作用于身管上的等效合外力，vt为不同时刻对应的弹丸运动速度。弹后空间为火药燃气作用区域，火药燃气压力作用于身管内壁的荷载条件随弹丸的运动而动态变化，属于时变动力学体系。

根据达朗贝尔原理[15]，计及阻尼和弹丸惯性效应，移动弹丸以及火药燃气压力作用下身管径向运动方程为

(1)

式中：EI(x)为身管的抗弯刚度；H为身管速度衰减系数；y(x,t)为身管x位置处t时刻的挠度；F为身管受载情况，可以近似为

F=δ(x-s(t))Fcont+∑ξ(x-s(t))P(x,t)ds

(2)

(3)

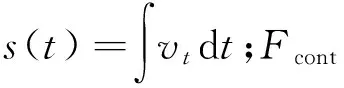
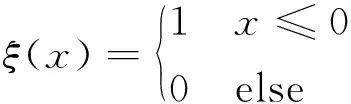
(4)

借助有限元分析软件建立物理离散模型，并利用中心差分法对相关力学模型进行计算分析。

2 弹炮耦合动力学有限元模型

本文以某122 mm口径榴弹炮为研究对象，建立基于弹炮耦合的火炮发射动力学模型，并计及火药燃气压力二维分布对身管动态响应的影响。

2.1 有限元模型

对火炮主要零部件进行离散建模，主要包括上架，摇架，后坐部分与弹丸等，对于不重要的附属机构以集中质量单元模拟，通过刚性单元与相邻节点连接模拟质量分布对结构强度的影响。上架与摇架结构主要采用等参四边形单元和等参六面体单元，平衡机简化为弹簧单元，高低机齿轮齿弧表面的接触采用刚性单元连接进行处理。身管膛线为混合膛线，用分段扫描拉伸方式沿膛线空间曲线扫描获得身管网格模型，身管坡膛处局部网格图如图2所示。弹丸弹体的变形不作为主体研究对象，故将弹体做刚性化处理，弹丸弹带处理为弹塑性，在弹带表面创建与身管膛线形状匹配的沟槽，以弹带完全挤进膛线时刻为数值计算起始时刻，预设沟槽弹带局部网格图如图3所示。

图2 线膛身管局部网格图Fig.2 Local view of rifled barrel mesh

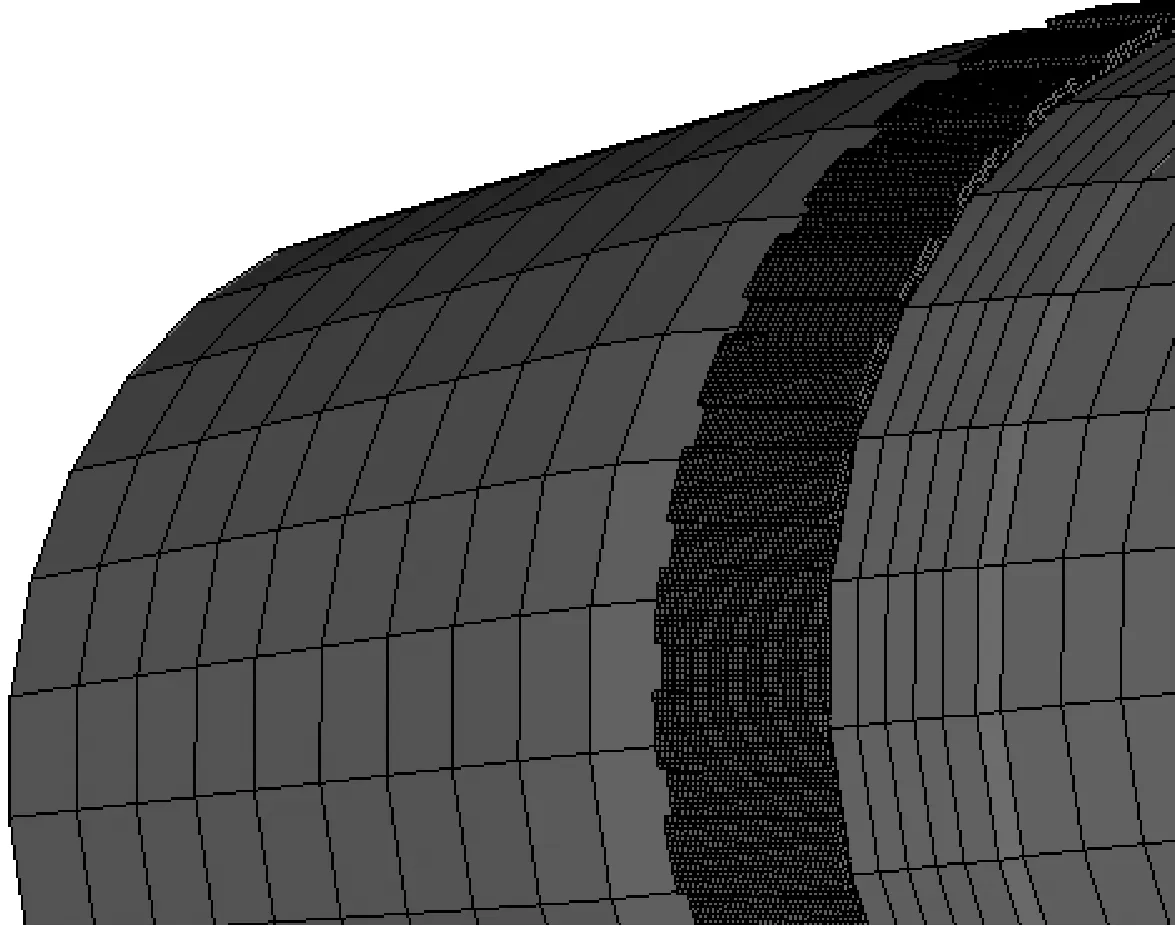
图3 预设沟槽弹带局部网格图Fig.3 Local view of band mesh with predefined groove

有限元模型中弹带与身管内壁之间定义为点-面接触，弹体前后定心部与身管内壁以及后坐部分与摇架导向部定义为面-面接触，均采用罚函数法进行处理。炮尾与反后坐装置之间则采用自由度耦合的方式模拟后坐部分在炮膛轴线方向的滑移运动，仅释放炮膛轴线方向的平移自由度，其他自由度均约束不动。摇架耳轴与上架耳轴室之间同样采用自由度耦合的方式定义，仅释放耳轴室中心轴线方向的转动自由度。

2.2 材料模型

内弹道过程中复杂的动态物理化学场使得弹带材料常常处在大应变、高温和大应变速率等综合因素下发生弹塑性应变。采用Johnson-Cook模型描述弹带材料塑性阶段力学行为[16]

(5)

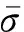
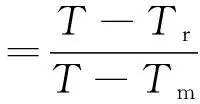
(6)

式中：Tr为参考温度，一般取室温；Tm为常态下材料的熔化温度。

身管采用炮钢材料PCrNi3MoVA，弹带材料为H96黄铜，对应的材料参数设置如表1所示。

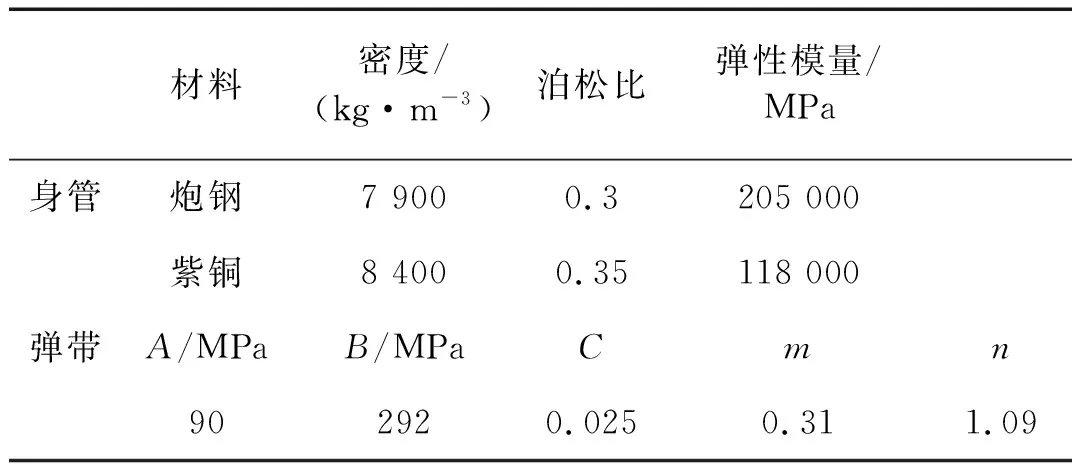
表1 数值计算涉及的材料相关参数Tab.1 Material parameters value for numerical computation

2.3 子程序实现内弹道物理场变化过程

火炮内弹道时期伴随复杂的物理场变化过程，主要体现在火药燃气压力变化以及对身管作用区域的变化，即二维分布特性。火药燃气一方面沿身管轴向流动，推动弹丸以及后坐部分完成内弹道运动过程。另一方面，火药燃气压力作用于弹后身管内壁，压力值与作用区域随着弹丸的运动而动态变化，可以根据实时测得的弹丸位置实现燃气压力二维分布情况。利用VUAMP以及VDLOAD子程序接口可以实现内弹道物理场变化过程。

2.3.1 推力子程序实现火药燃烧过程

多数学者采用弹底加载实测内膛压力曲线的方法实现弹丸主动力的加载，采用这种方法相当于计及了两次次要功，其弹丸出膛参数的准确程度不高[17]，并且该压力曲线并不能表征数值模拟对应的实际内弹道过程。应用推力子程序(VUAMP)可以实现内弹道火药燃烧规律与弹丸膛内运动的关联效应。针对整个内弹道耦合过程做如下假设：

(1) 忽略内弹道起始时刻对应的弹丸卡膛以及弹带挤进过程，假定挤进完成时膛内平均压力为30 MPa，设为膛压初始值。

(2) 以炮膛底面中心点为坐标原点，身管轴线指向炮口方向为x轴正向，基于拉格朗日模型假设得到的气体压力分布作为弹后空间身管内壁的载荷分布，弹后空间的气体压力呈抛物线分布，如下所示

(7)

式中：st为弹丸运动位移；φ为二次功系数；Pt为火药气体平均压力。

由上式可知，弹底压力写为平均压力的函数为

(8)

膛底压力写为平均压力的函数为

(9)

利用Fortran语言对火药燃烧过程编译，在每个计算增量步，数值计算模型实时传输弹丸运动参量，子程序计算得到相应的实时内膛平均压力Pt，并传入有限元模型。弹底压力Pd由式(9)计算得到，推动弹丸完成膛内运动过程。膛底压力由式(10)计算得到，并作为后坐运动主动载荷作用于膛底表面。

本计算模型采用的是模块化装药，相应的经典内弹道方程组可表示如下

式中：z为药粒相对燃烧厚度；ψ为相对已燃体积；χ，λ，μ为与药粒形状相关的内弹道参数；w为装药量；f为火药力；l0，l(t)为药室缩颈长、弹丸行程；u1，e1，n为火药燃烧系数，火药弧厚，燃烧指数；θ为热力指数；S为炮膛断面面积。

2.3.2 荷载条件子程序实现身管内壁受载过程

膛内燃气压力作用于弹后身管内壁，受载区域随弹丸运动而动态变化，利用荷载条件子程序(VDLOAD)实现身管实际受载情况。以时间增量步为单位，主程序对子程序进行调用运算，子程序主要实现步骤如下：

步骤1主程序向子程序传输实时弹丸运动位置l(t)，实时火药燃气压力Pt。

步骤2以身管内表面所有积分点为加载单元，子程序依据主程序获取所有积分点的轴向坐标。

步骤3子程序进行相关判断分析以及赋值燃气压力。依次对每个积分点进行赋值，在满足对应积分点的轴向坐标小于弹丸运动位移的情况下，将对应位置的实时火药燃气压力赋予该积分点。

步骤4所有积分点赋值结束，返回主程序。

在每次子程序调用过程中，整个子程序实现流程示意图如图4所示。

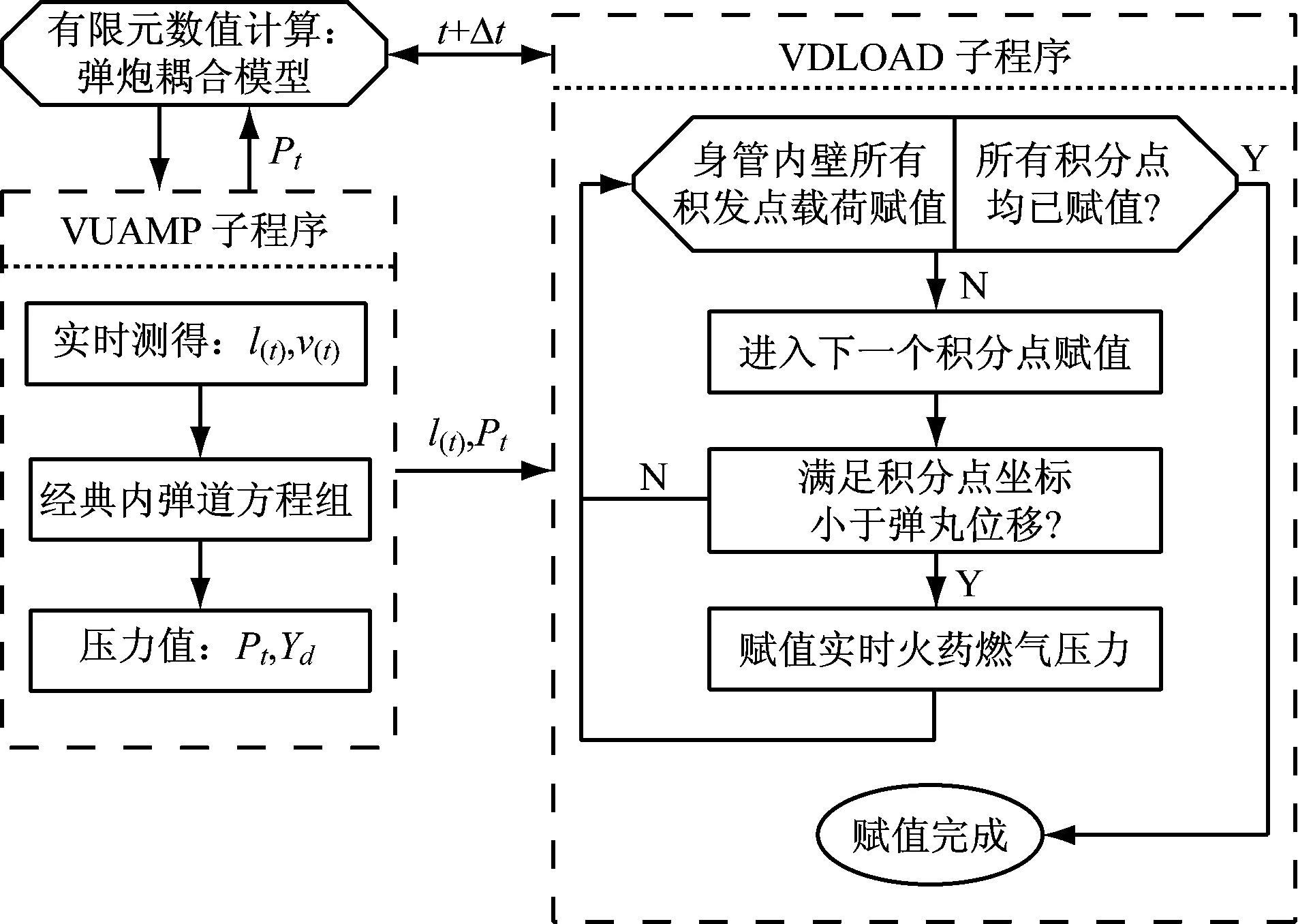
图4 子程序实现流程示意图Fig.4 The flow diagram of subroutine operation

3 数值仿真结果分析以及实验对比

3.1 再现身管应力响应动态过程

图5显示了不同时刻对应的身管截剖面动力学响应情况，图中隐藏弹带部件是为了清晰观察身管的应力分布。从图中可清晰看到不同时刻弹丸在膛内的运动位置，身管主要应力分布在弹后区域，身管的受载面积随弹丸的运动而动态变化，与实际发射环境相一致，实现了火药燃气压力作用于身管内壁的实际荷载条件。

图5 身管轴向截剖面应力分布云图动态变化过程Fig.5 Dynamic change process of stress distribution in axial cross section of barrel

3.2 实弹射击实验简述

为了验证所建立的非线性动力学模型的正确性，进行了该型号火炮实弹射击试验，将火炮上架及以上部分固结于发射台。采用七维航测科技公司的SDI-ARG-720型角陀螺传感器，用于测量炮口高低方向的运动角参量，数据采集系统为DEWETRON 1201系统，试验中角陀螺仪在身管上的布置位置如图6所示。

采用非接触式测试系统获取炮口振动位移参量，在炮口外表面布置和标定专用的测试标识，运用高速摄影系统记录到测试标识的运动轨迹，并通过专用的分析系统处理进而得到相应的振动参数。高速摄影设备采用IDT公司生产的Y3-S2高速摄影机，光学镜头为Nikkor AF-S 400mm F2.8D ED镜头，采用Xcitex公司开发的ProAnalyst软件对图像进行跟踪处理。高速摄影系统及其支架固定在炮口侧面的地面上，其布置示意图如图7所示。射击工况与数值模拟工况相同，为0°射角。

图6 角陀螺仪装配实物图Fig.6 The assemble paragraph of angle gyroscope

图7 高速摄影系统布置示意图Fig.7 The arrangement diagram of high-speed camera system

3.3 炮口振动参量对比分析

数值模拟火炮射击过程，在与实验对应的炮口振动实测位置设置细小的杆单元，并通过耦合建模与身管进行连接，得到炮口振动量的时程变化曲线，并与试验测得的数据进行对比。图8和图9为通过实弹射击试验获取的炮口测试点振动垂向位移和角位移与仿真数据的对比。从图中可以看出，仿真得到的炮口测试点的位移和角位移时程变化情况与试验测得的数据吻合较好。本文以弹丸弹带脱离时刻为弹丸出炮口的度量标准，弹丸出炮口时刻对应的炮口振动量结果对比如表2所示，误差均在可接受范围之内，有效验证了本文计及身管实际受载火炮发射动力学模型的正确性。

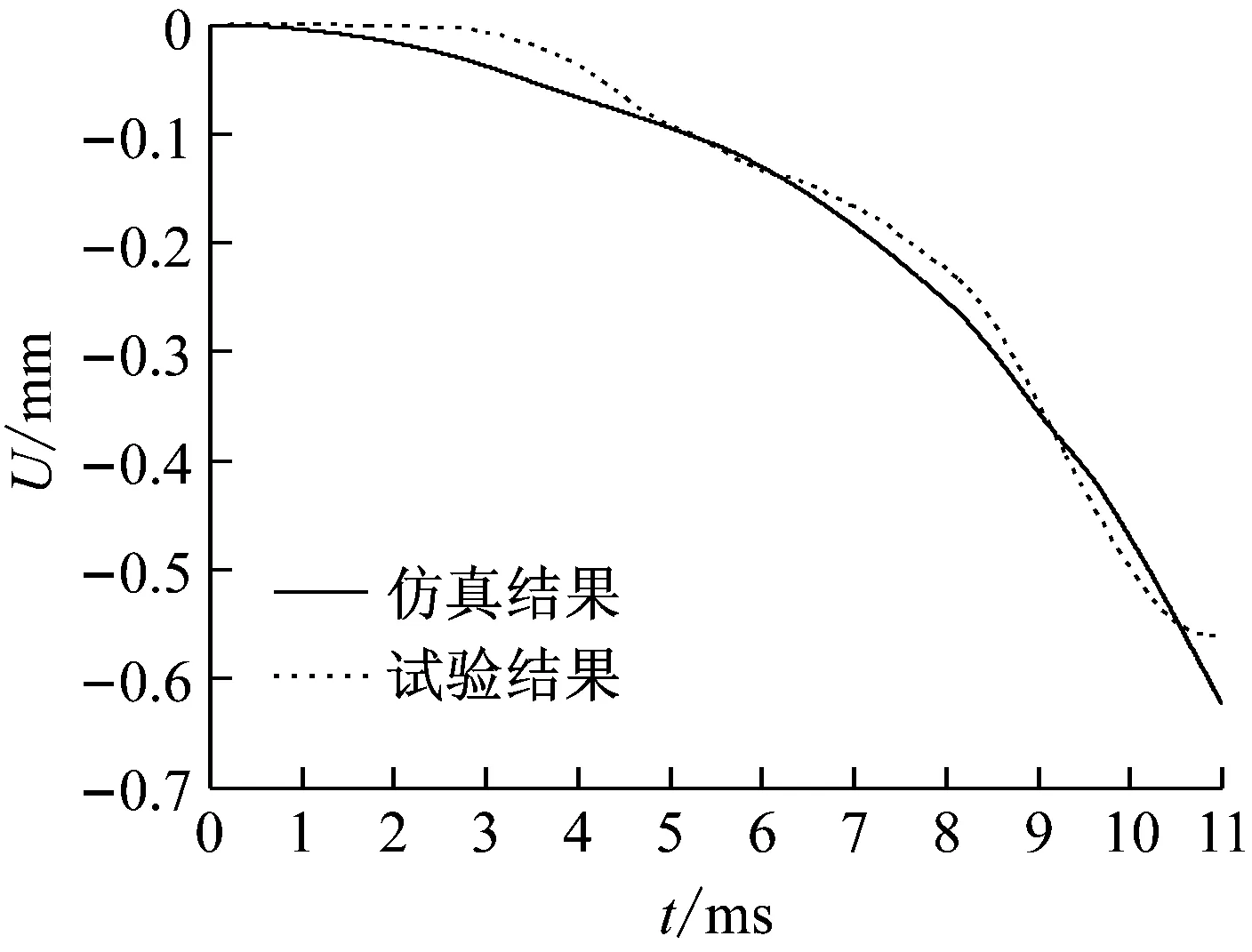
图8 炮口垂向线位移Fig.8 The muzzle displacement in vertical direction

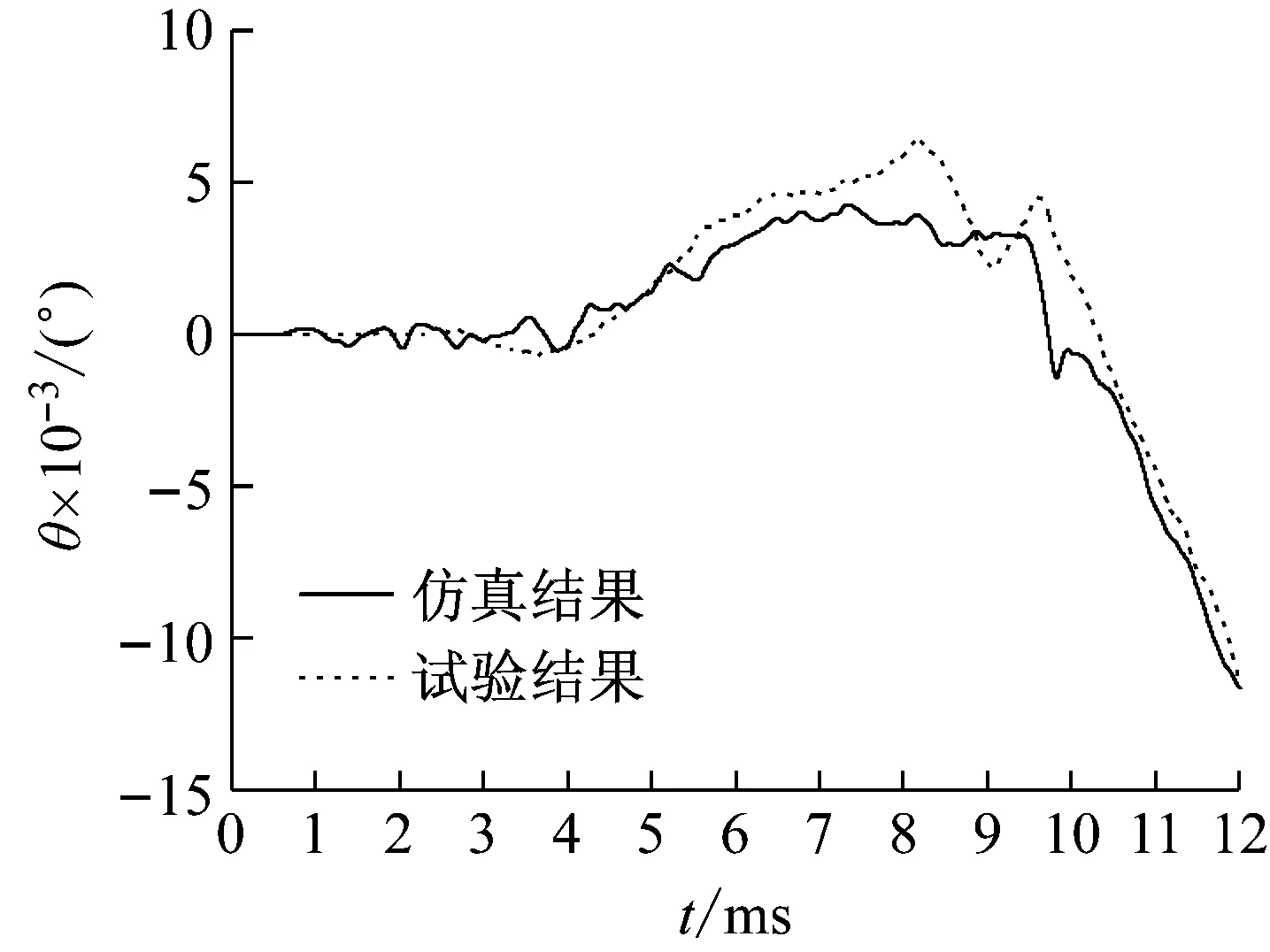
图9 炮口垂向角位移Fig.9 The muzzle angular displacement in vertical direction

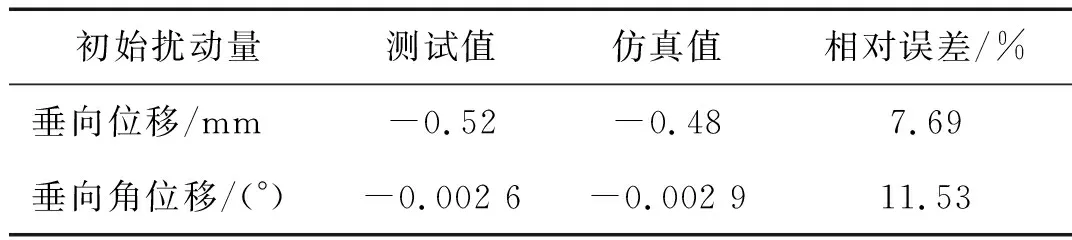
表2 炮口初始扰动测试与仿真结果对比Tab.2 Comparison of muzzle initial vibration by test and simulation

3.4 身管动力学响应

现有的关于火炮身管振动以及身管强度数值分析的文献中，由于燃气压力径向效应加载不准甚至无法加载的问题，大部分仅考虑了燃气压力的轴向效应，而忽略了燃气压力二维分布特性对身管动态响应的影响。为有效表述燃气压力径向效应对身管动力学响应的影响，预先设置了两种数值模拟环境：计算工况一，仅考虑高压火药气体轴向效应，不考虑身管径向受载；计算工况二，综合弹炮耦合与身管径向受载，计及火药燃气压力二维分布特性，由子程序根据弹丸实时运动位置定义载荷大小与分布。

3.4.1 身管振动响应分析

图10与图11分别显示了两种数值模拟环境下炮口在垂向以及水平方向的振动情况。综合垂向以及水平方向炮口振动曲线可知，计及燃气压力作用下，身管振动较剧烈。高压气体冲击线膛身管内表面，膛线的存在使得身管整体受载不对称，在水平面内的振动情况呈现一定的波动，且振动幅度明显强于仅考虑燃气压力轴向效应的情况。由得到的炮口振动曲线可知，膛内燃气压力对身管振动具有直接影响，因此在数值模拟研究身管振动问题时，准确描述火药燃气压力二维分布特性是必要的。

图10 炮口垂向线位移Fig.10 The muzzle displacement in vertical direction

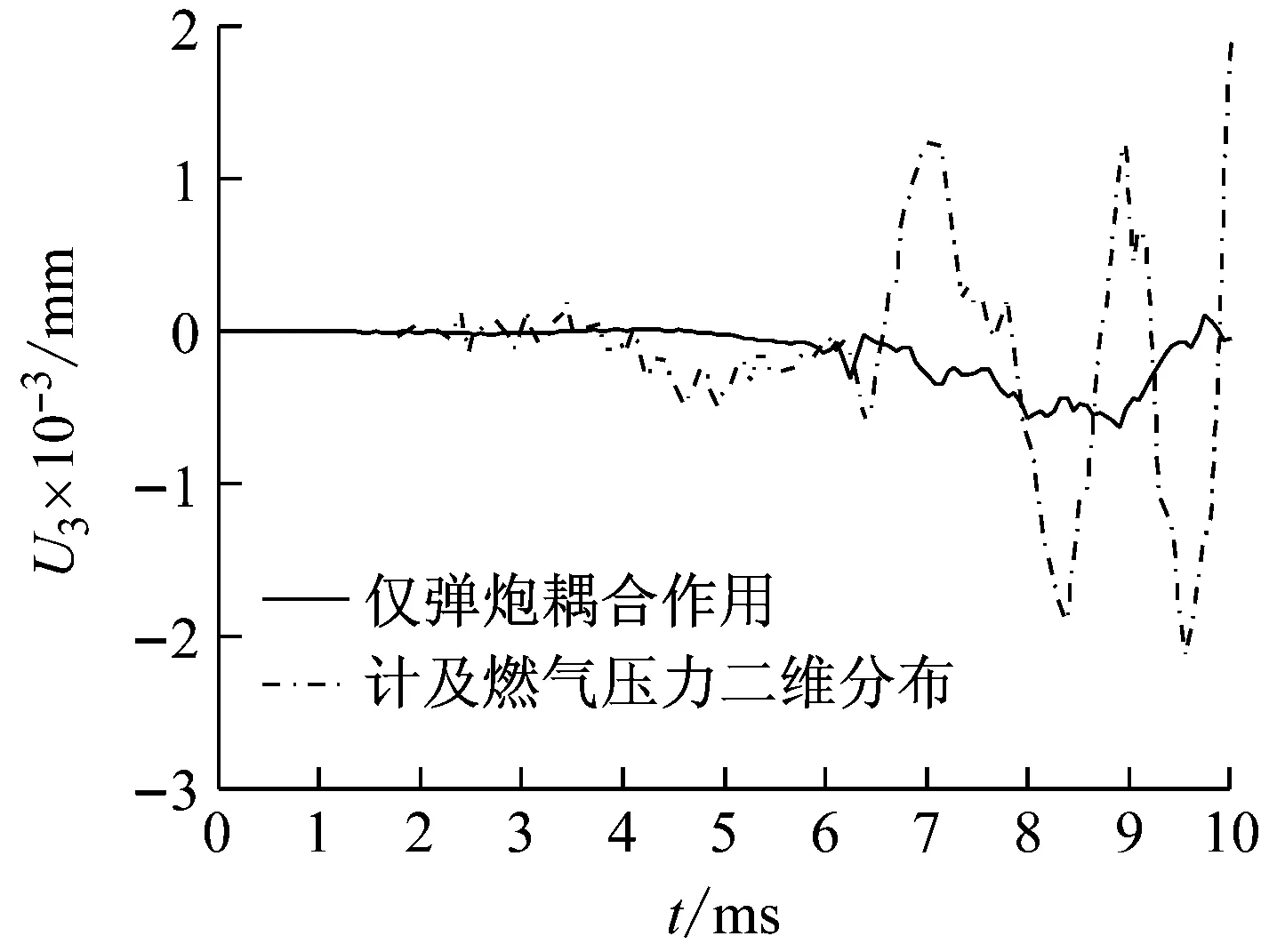
图11 炮口水平方向线位移Fig.11 The muzzle displacement in horizontal direction

3.4.2 身管动态强度分析

为捕捉身管应力响应随时间的变化情况，在身管内壁沿轴向等间距选取四个积分单元，A积分点靠近药室部，并依次向炮口方向选取B，C，D三个积分点，得到对应的应力时程曲线。图12对应仅考虑弹炮耦合作用的情况，身管主要受到弹丸与身管相互接触碰撞产生的载荷，身管局部指定区域应力响应短暂。运动的初始时刻，弹丸惯性效应不明显，与身管接触碰撞产生的载荷较小，与弹丸接触区域应力幅值变化不明显。随着运动的进行，身管应力幅值曲线的峰值与弹丸运动速度具有正相关。图13对应计及火药燃气作用于身管内壁的情况，数值计算得到的身管指定位置应力幅值曲线反映了火药气体实际作用情况，与不计及火药燃气作用于身管内壁的情况相比，更能反映出身管实际动力学响应。

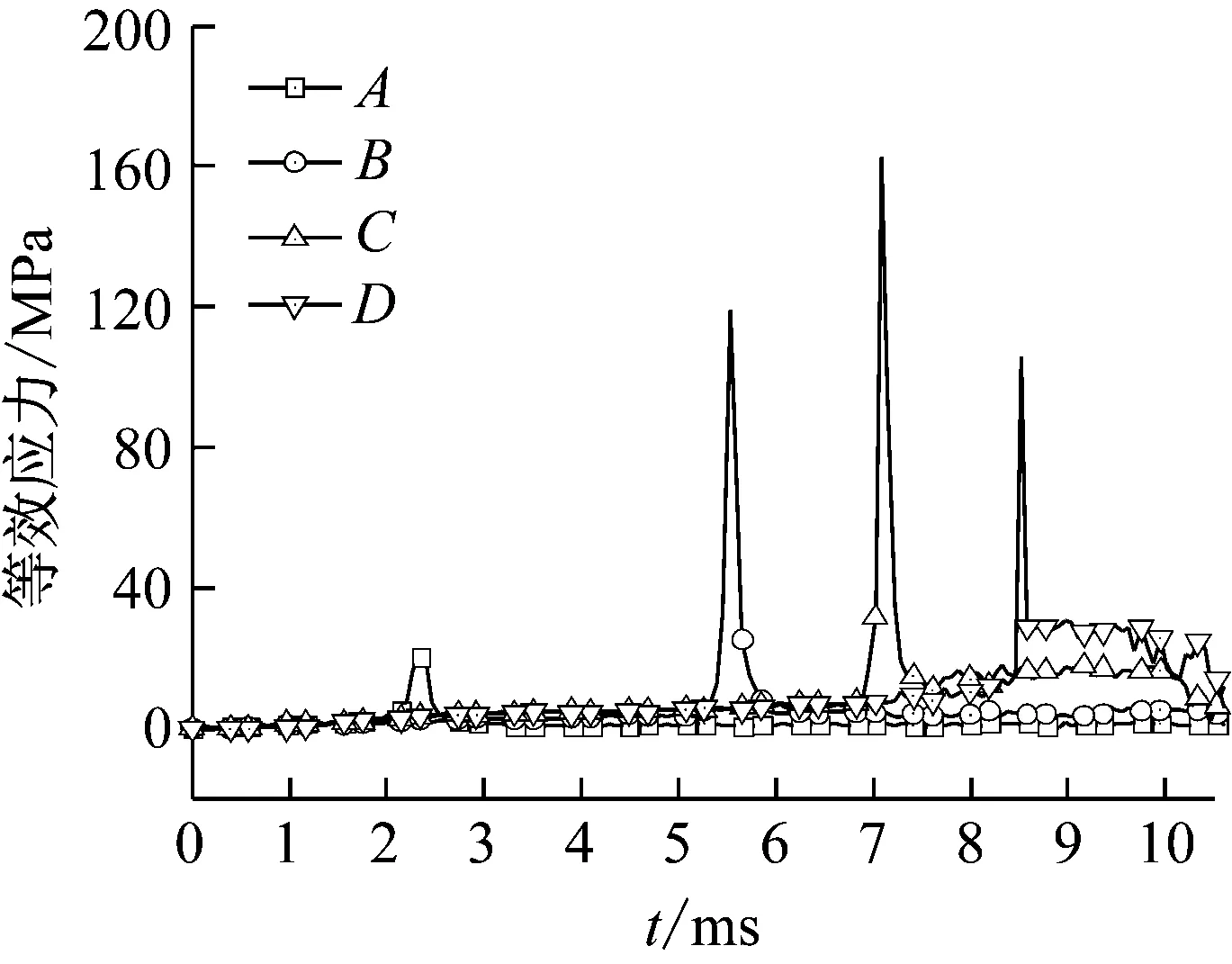
图12 仅考虑燃气压力轴向效应下身管应力时程变化曲线Fig.12 Stress-time curves of barrel under axial effect of gases pressure

传统身管设计依据静强度设计理论，通过最大径向压力确定身管各部位的安全系数，而身管径向受载属于与二维分布有关的动态过程,文献[13]指出身管强度设计按动态问题处理才是符合实际的设计。图14显示了两种数值模拟环境下得到的身管应力峰值时程分布曲线。仅考虑弹炮耦合作用下，身管应力响应随弹丸速度的增加呈现递增的趋势，取决于弹丸的惯性力。计及火药燃气压力与弹炮耦合作用下，身管应力响应较剧烈，在身管强度分析方面更具说服力。整个动力学过程身管等效应力峰值曲线最大值为508 MPa，位于弹丸导向部，对应火药燃气压力最大值时刻。由Von Mises屈服准则可知，身管材料的屈服应力为1 040 MPa，安全系数大于2，符合身管强度要求，高压火药燃气以及弹炮耦合作用下身管处于较安全状态。

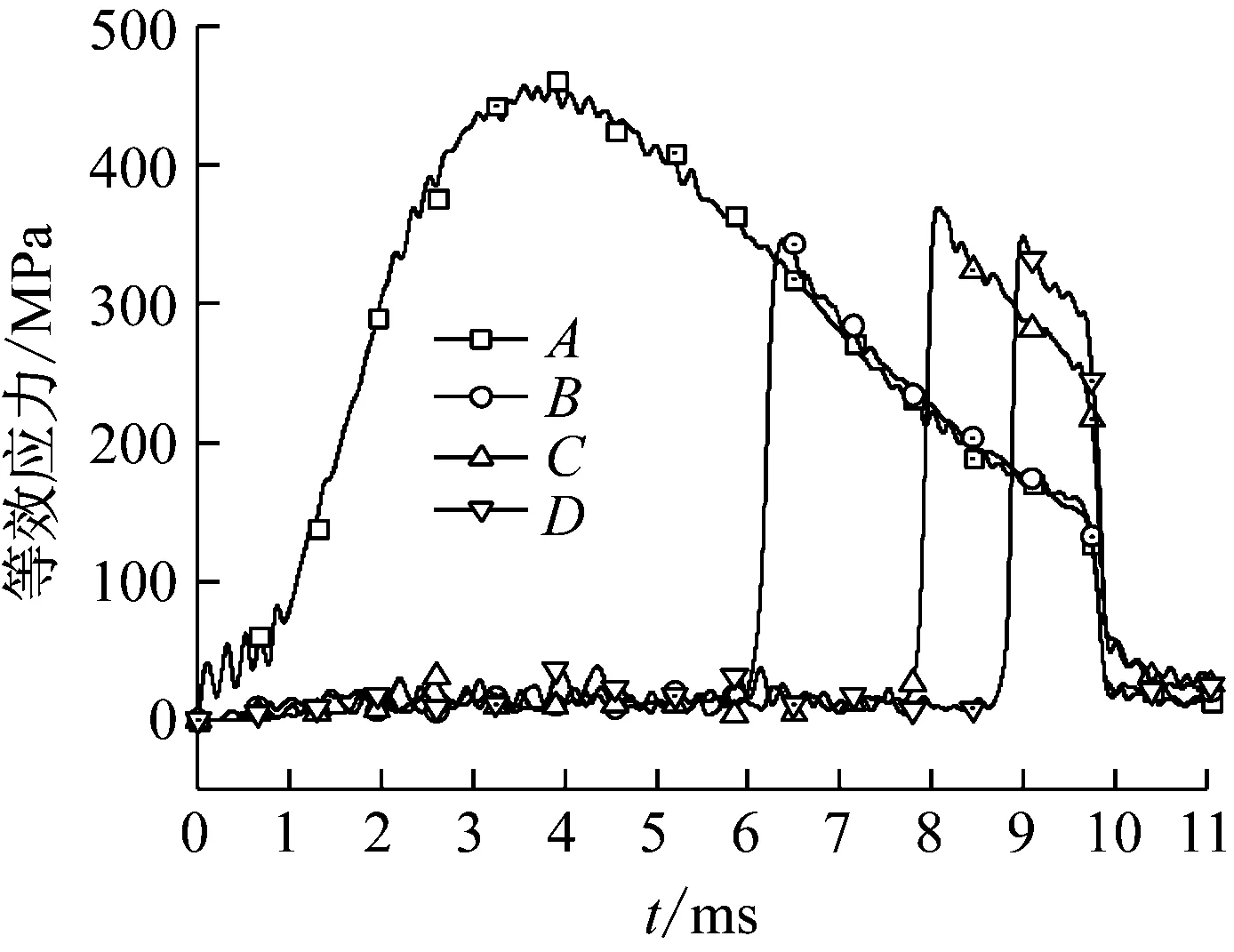
图13 计及径向受载身管应力时程变化曲线Fig.13 Stress-time curves of barrel considering gas pressure

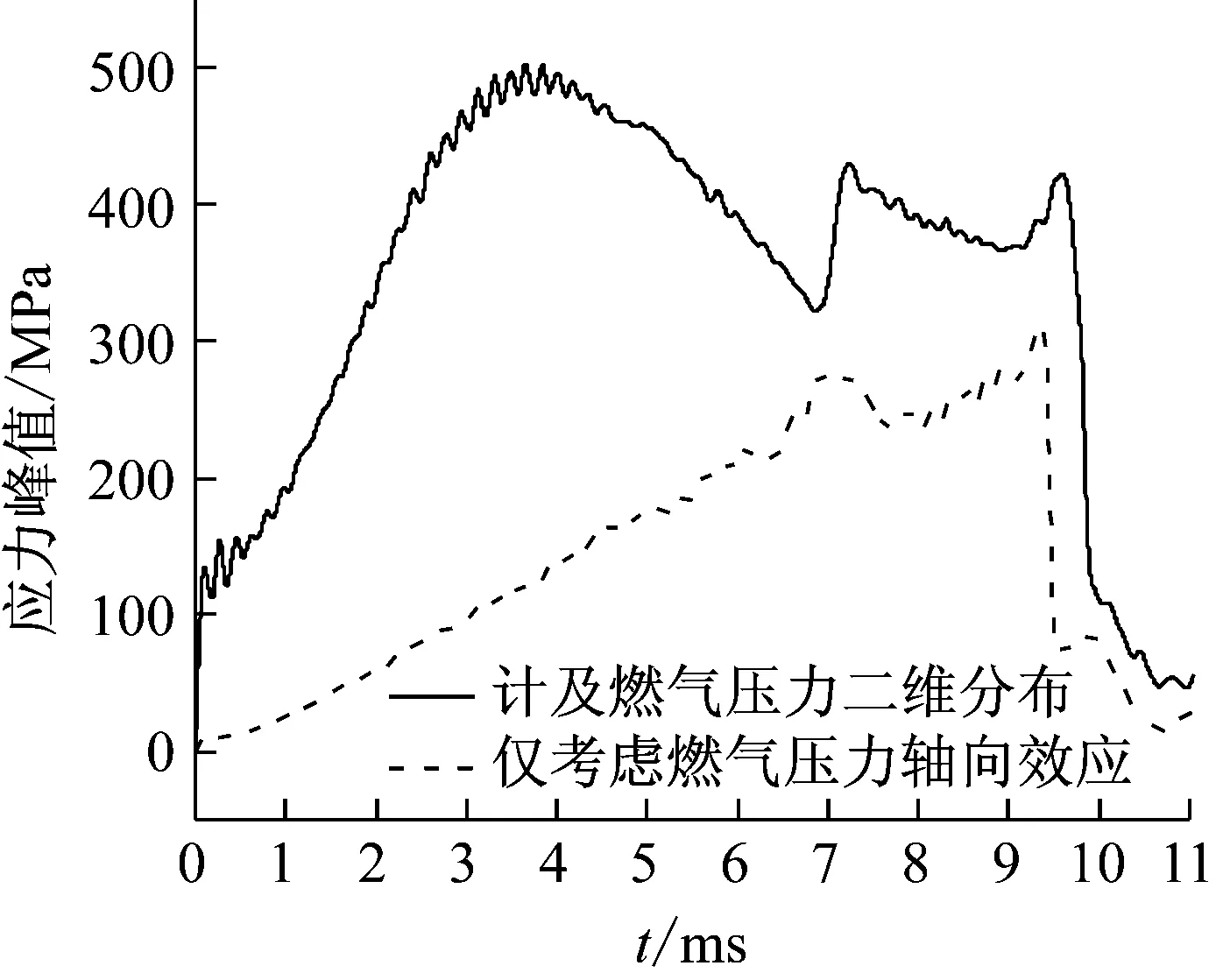
图14 身管应力峰值时程分布曲线Fig.14 Stress peak distribution curves of barrel in time domain

4 结 论

本文在现有的基于弹炮耦合火炮发射动力学模型的基础上，考虑到高压火药燃气的冲击作用对身管动力学响应的影响，借助有限元软件提供的用户自定义子程序，实现了弹丸膛内运动与经典内弹道火药燃烧相互关联过程，同时实现了膛内火药燃气压力二维分布特性，解决了以往燃气压力径向效应加载不准甚至无法加载的问题。结合实弹射击实验，验证说明了所建立的数值模型是可取的，为火炮发射过程的数值模拟提供了更接近实际的物理场边界条件。通过对比分析身管在有无燃气压力径向效应数值模拟环境下的动力学响应可得出如下结论：

(1) 由于燃气压力对线膛身管的冲击效应，身管在计及燃气压力二维分布特性条件下的振动响应明显强于仅考虑弹炮耦合的情况，说明在数值模拟研究身管振动问题时，准确描述火药燃气二维分布特性是必要的。

(2) 计及燃气压力二维分布的火炮发射动力学数值模拟可以得到接近实际物理场作用下的结构强度响应，为今后火炮设计以及故障分析提供了更具说服力的参考依据。