区间模型下声子晶体的带隙优化研究

刘 坚, 陈俊煌, 夏百战, 满先锋

(湖南大学 汽车车身先进设计制造国家重点实验室, 长沙 410082)

声子晶体是一种新型功能材料，其组分的材料参数呈周期性变化。声子晶体带隙的形成机理通常有两种，分别是Bragg散射机理[1]及局域共振机理[2]。Bragg散射形成的弹性波带隙所对应的波长一般和晶格常数相当，其第一带隙的中心频率处所对应的波长一般为晶格常数的两倍。Bragg散射的这一特性有碍于低频减振降噪。Liu等[3]在2000年提出了局域共振声子晶体概念。他将硅橡胶包裹的铅球按简单立方晶格排列方式，周期性地嵌入环氧树脂基体中，形成三维三组元声子晶体。这种声子晶体产生的带隙所对应的波长比晶格常数大两个数量级，突破了Bragg散射的波长限制。Goffaux等[4]理论上证实二维三组元声子晶体同样存在局域共振带隙，并结合类Fano现象和近似的机械振动模型初步揭示了局域共振带隙的形成机理。Ho等[5]在实验室制得了可用于低频隔音的局域共振材料。Zhang等[6-7]发现在局域共振型声子晶体的高频段存在较宽的带隙。Hirsekorn等[8-9]分析了三种不同材料组成的二维声子晶体的传播性质。

几何结构参数对于声子晶体声学特性的影响较大。改变声子晶体的结构参数，能改变声子晶体带隙宽度及带隙范围等。基于这一性质，优化设计逐渐被应用于声子晶体优化设计。Romero-Garcia等[10]通过对孔的分布形状及数量进行优化，使得声子晶体中的声波聚焦和稀疏性能得到改善。通过对共振腔形状尺寸的优化，Wang等[11]得到了具有完全带隙的三维孔状声子晶体。这些优化都是基于确定性物理模型。在实际工程应用中，由于制造误差和测量误差，以及多变的环境因素和不可预测的外部激励，声子晶体的不确定性是难以避免的。声子晶体带隙对这些不确定参数比较敏感，XIA等[12]在最近的一篇文章研究发现，霍姆赫兹共振腔声子晶体的带隙及有效体积模量对水温的变化比较敏感。如果不考虑这些不确定性因素，会导致得到的优化结构不可靠。因此，在对声子晶体进行优化时，需要考虑不确定性参数的影响。

概率模型是常用的不确定数值分析模型。然而在样本数据有限的情况下，通常难以获得不确定参数精确概率密度函数。针对这种情况，Moore[13]提出了区间模型的方法。Monte-Carlo法[14]是种最简单最稳健的区间分析方法。夏日战等[15]将区间不确定模型引入声学超材料，采用Monte-Carlo 法分析区间不确定性对声学超材料性能的影响；接着在此基础上，构造区间模型下声学超材料的可靠性优化模型，采用优化算法对优化模型进行求解。根据Monte-Carlo 法的概率收敛性，其计算精度随着样本数据的增加逐渐提高。但是巨额的计算负担使Monte-Carlo 法难以适用于复杂的工程实际问题[16]。Liu等[17]利用Chebyshev展开法分析不确定非线性系统动力学响应分析。Xia等[18]采用Chebyshev展开法分析时变区间模型下结构的动态响应。Wu等[19-20]将Chebyshev展开法应用于区间模型下汽车动力学分析和多体机械系统的不确定分析。

目前，国内外对于声子晶体的研究基本都是在确定几何尺寸、材料属性、环境因素的情况下进行，而鲜有关于声子晶体的不确定性研究。针对这一情况，本文将区间分析方法引入声子晶体，对其进行不确定分析。本文将两个不确定性变量与两个设计变量作为Chebyshev多项式的四个变量，构建每条能带的Chebyshev代理模型，并基于该代理模型用Monte-Carlo 法求解能带的变化区间。以声子晶体带隙最大化为目标函数，以期望带隙为约束条件，构建基于Chebyshev代理模型的区间声子晶体可靠性优化模型。最后，采用遗传算法对该区间优化模型进行求解。该方法的优点是只需一组初始的有限元计算数据构建Chebyshev代理模型，后续优化皆基于计算效率较高Chebyshev代理模型，避免了传统优化方法中有限元模型的重复计算，极大地减小了计算负担。

1 能带结构的有限元计算方法

对于各向同性的线弹性体材料，角频率为ω的弹性波传播方程为

(1)

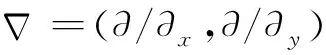
(2)

(3)

图1(a)为声子晶体单胞。根据Bloch定理[21]，位移向量u(r)可以用如下公式表示

u(r)=ei(k·r)uk(r)

(4)

其中，uk(r)表示周期性矢量函数，k=(kx,ky)表示第一布里渊区的波矢量，如图1(b)所示。

用有限元方法数值求解方程(4)，得到离散化的广义特征值方程如下

Ku=ω2Mu

(5)

式中:K和M分别表示整体的刚度矩阵及质量矩阵;u表示节点位移。

刚度矩阵和质量矩阵的计算公式为

(6)

(7)

式中:B表示应变矩阵;N表示形函数矩阵;Ve表示整个单胞区域。

假设波入射方向上有N个声子晶体单胞，边界则满足Born-von Karman条件[22]

f(r)=f(r+Na)

(8)

式中:a表示晶格基矢;N表示整数;f(r)表示在波矢方向的周期函数，其周期性为a。

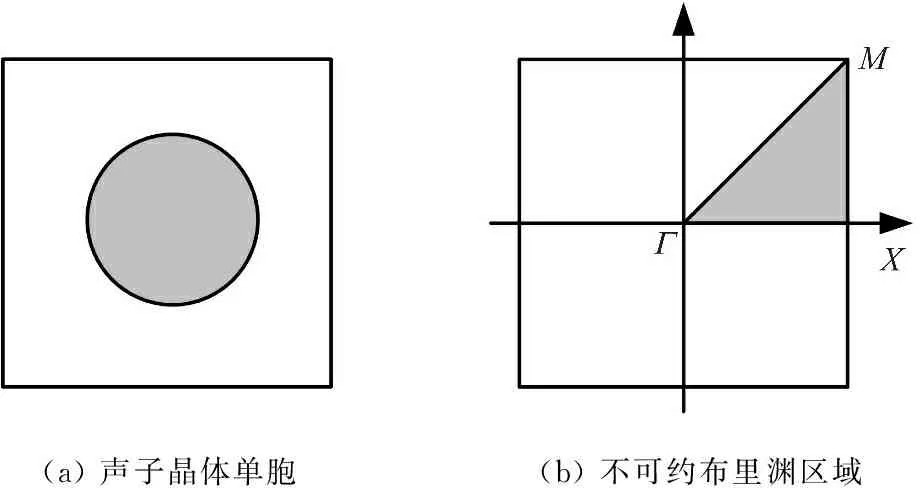
(a) 声子晶体单胞(b) 不可约布里渊区域

图1 声子晶体单胞有限元模型及其不可约布里渊区域

Fig.1 Finite element model of the phononic crystal unit cell and the corresponding irreducible Brillouin zone

将式(5)和(8)联立，即可求解给定波矢k下的特征频率。将求得的特征频率代到控制方程(1)中，即可得到该频率下的本证模态u(r)。将波矢k对单胞结构的不可约Brillouin区进行扫掠，即可得到该声子晶体的能带结构。

2 区间模型的构造及可靠性优化理论

减振降噪是声子晶体的一个重要性能。局域共振声子晶体能够用小尺寸产生低频带隙，突破Bragg散射的波长限制，从而为声子晶体在低频减振降噪方面的应用提供了可能。本文将不确定区间模型引入局域共振声子晶体，以带隙最大化为目标函数，以期望频带为约束，构建区间模型下声子晶体的可靠性优化模型，并采用Chebyshev展开法对局域共振带隙进行优化。

2.1 Chebyshev展开法

Monte-Carlo法可用于区间模型下声子晶体带隙分析。但其高昂的计算成本严重限制其工程应用价值。本节讨论将Chebyshev多项式展开引入到区间声子晶体不确定性分析，构建区间声子晶体的Chebyshev代理模型。

对于，第n阶Chebyshev多项式定义如下[23]

Cn(x)=cos (nθ)

(9)

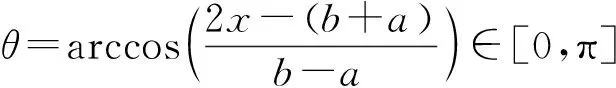
其中n表示非负整数。在区间上，Chebyshev多项式的递推关系可表示如下

(10)

L个变量的Chebyshev多项式定义为

Cn1,n2,…,nx(x1,x2,…,xL)=

cos (n1θ1)cos (n2θ2)…cos(nLθL)

(11)

其中，θi=arccos(xi), (i=1, 2, …,L)

声子晶体的能带曲线的Chebyshev多项式表示如下[24]

fs(x,[WTHX〗k)=

(12)

其中,p表示下标i1,i2,…,iL等于零的数量。下标s(s=1,2,3…,10)表示第s条能带。fi1,…,iL(k)表示多项式系数。向量x包含L个变量。系数fi1,…,iL(k)为波矢k的函数。

系数fi1,…,iL(k)可由下式推得

fi1,i2,…,iL(k)=

cosi1θ1…cosiLθL)dθ1…dθL

(13)

其中,L表示变量数，下标i1,…,iL=0,1,2,…,n。

用梅勒积分公式[25]进行转换后可得到

Ci1,…,iL(xj1,…,xjL) ≈

cosi1θj1…cosiLθjL

(14)

直接基于有限元模型，采用Monte-Carlo法分析声子晶体带隙的变化范围，其计算精度随着样本量的增加而趋于精确解。但是有限元模型的反复计算会带来巨额的计算负担。通过Chebyshev代理模型替换有限元模型，仅需采用有限的样本数据构造Chebyshev多项式，极大地提高了声子晶体带隙的分析效率。

2.2 区间可靠性优化模型

声子晶体的带隙特性是声子晶体的重要特性之一。带隙的最大化可以使得声子晶体的禁带变宽，在工程实际中降噪效果更为明显。因此，本文的目标函数是声子晶体带隙的最大化。可以表达为

max{Fmax-Fmin}

(15)

式中带隙的下边界频率Fmin和上边界频率Fmax可以表示为

Fmin=inf{Δf}

Fmax=sup{Δf}

(16)

其中，Δf表示带隙。由于不确定参数的存在，Fmin和Fmax均不是一个确定的数值，而是一个变化的区间。图2为声子晶体能带的局部放大图，图中Fmin,1和Fmin,2分别表示带隙下边界频率Fmin变化区间的下限及上限。Fmax,1和Fmax,2分别表示带隙上边界频率Fmax变化区间的下限及上限。以区间[Fmin,2,Fmax,1]的最大化为优化目标，优化后的带隙是保守的。若以区间[Fmin,1,Fmax,1]、[Fmin,2,Fmax,2]或[Fmin,1,Fmax,2]中的任意一个为优化的带隙时，由于不确定参数导致的带隙区间波动，实际带隙不一定完全处于目标区间中，优化结果存在一定的风险。

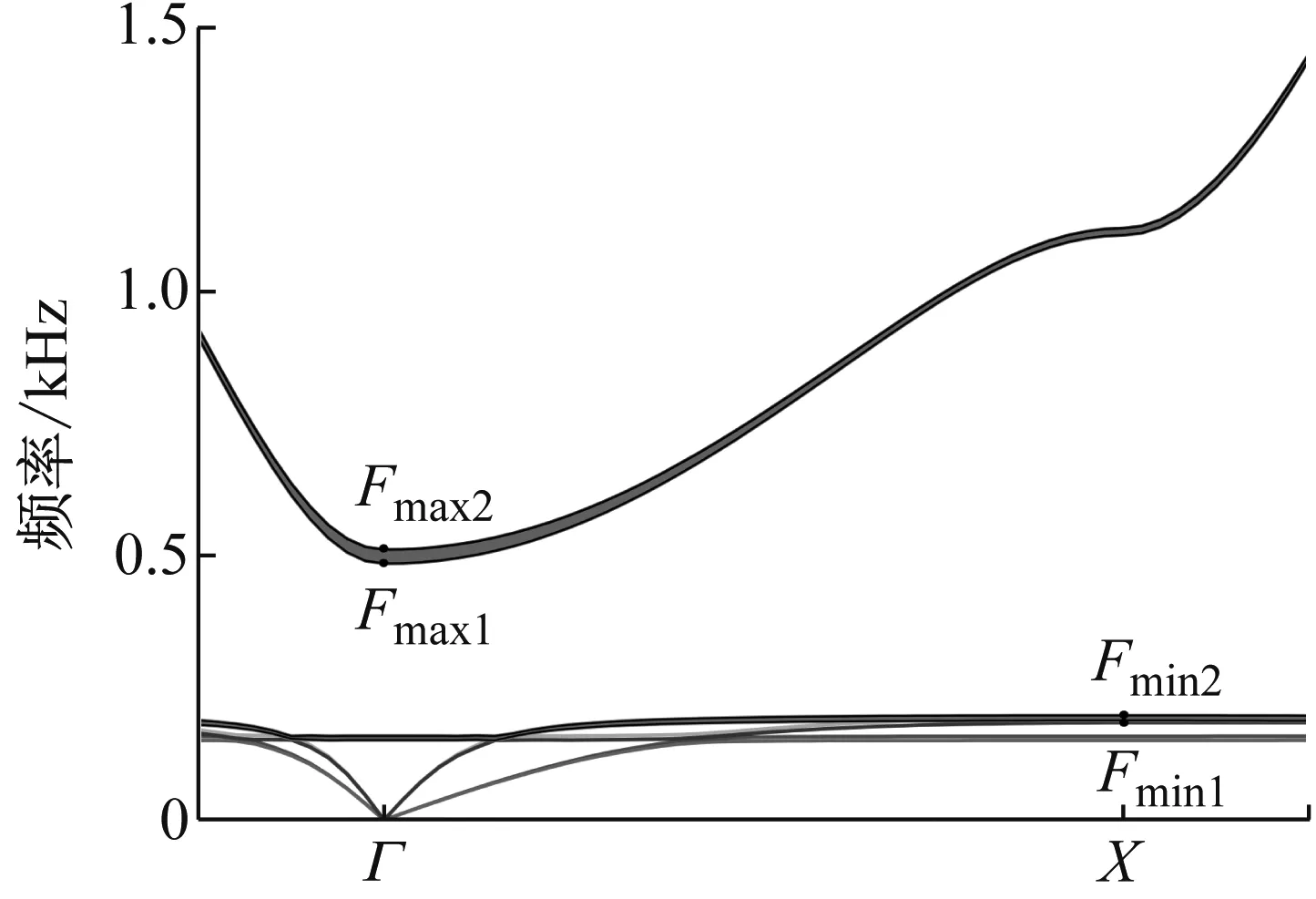
图2 声子晶体能带局部放大图Fig.2 Local enlarged drawing of phononic crystal energy band

因此，本文以区间[Fmin,2,Fmax,1]变化范围的最大化为目标函数，式(15)的更为具体的表达形式应为

max{Fmax,1-Fmin,2}

(17)

其中，Fmax,1和Fmin,2可用如下形式表示

⋮

⋮

(18)

在实际工程应用中，某个频率段的噪声或振动对于生产是有害的，因此往往需要屏蔽特定频率段的振动或噪声。本文将期望的频带作为约束条件，若[f1,f2]为所期望的频带，则目标函数中的带隙[Fmin,2,Fmax,1]的上边界频率Fmax,1要不小于f2，下边界频率Fmin,2要不大于f1。该约束条件可表示为

Fmin,2≤f1≤f2≤Fmax,1

(19)

综上可知，声子晶体的区间可靠性优化模型为

max {Fmax,1-Fmin,2}

(20a)

s.t.Fmin2≤f1≤f2≤Fmax 1

⋮

⋮

(20b)

2.3 区间可靠性优化模型的优化流程

遗传算法模拟达尔文的进化论机理来寻找最优解，其过程简单，又具有很好的收敛性与鲁棒性。因此，本文选用遗传算法作为优化算法。以Chebyshev代理模型为基础，声子晶体区间优化模型的求解流程如下：

步骤1将设计变量R1…Rn作为个体进行编码，并生成一组初始群体；

步骤2基于Chebyshev代理模型，用Monte-Carlo 法求解能带的变化范围，计算个体适应度值；

步骤3计算约束条件的值；

步骤4判断可靠性约束条件是否成立？若成立，则进行下一步；若不成立，则更新上一个群体，并回到第二步；

步骤5判断是否达到演化循环次数(给定的演化循环次数为10 000次)，若达到则结束并输出结果；若未达到则对群体P(t)进行一轮选择、交叉、变异运算之后可得到新一代的群体P(t+1)，并回到第二步。

3 数值算例

3.1 含梳状夹层二维局域共振声子晶体模型

本文所采用的声子晶体为含梳状夹层的声子晶体[26]，如图3所示。它的内核为金属，基体为聚合物，中间的夹层呈梳状，由橡胶和空气交替组成。声子晶体的晶格常数为a，中间梳状橡胶夹层由16个均匀分布的扇形单元组成，每个扇形单元的中心角为π/8，夹层的内外半径分别是r1和r2。聚合物基体的材料参数分别是ρ=1 200 kg/m3，E=3.5×107Pa，γ=0.49。金属内核的材料参数分别是ρ=8 950 kg/m3，E=2.1×1011Pa，γ=0.29。几何参数初始值分别为a=20 mm，r1=5.4 mm，r2=8.0 mm。

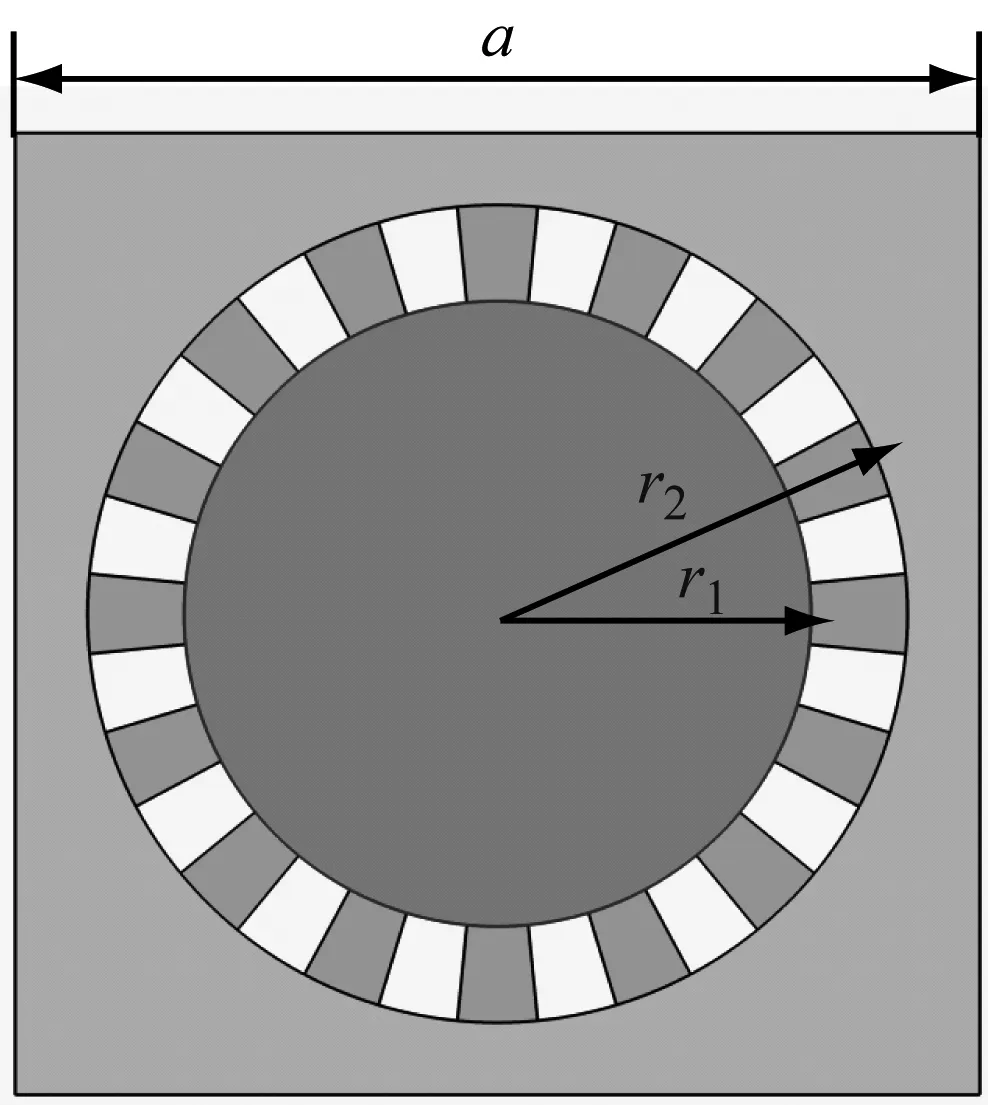
图3 含梳状夹层的声子晶体单胞Fig.3 Phononic crystal unit with a comb like coating

3.1.1 几何结构参数对带隙的影响

几何结构参数是影响声子晶体带隙的一个重要因素。本节将探讨夹层内半径r1和外半径r2对声子晶体带隙的影响。表1为几何参数r1和r2的变化情况。其中，Case1表示外半径r2和晶格常数a保持不变，而内径r1从5 mm逐渐变化到7 mm；Case2表示内径r1和晶格常数a保持不变，而外径r2从7.5 mm逐渐变化到9.5 mm。Case1和Case2所对应的带隙变化如图4所示。

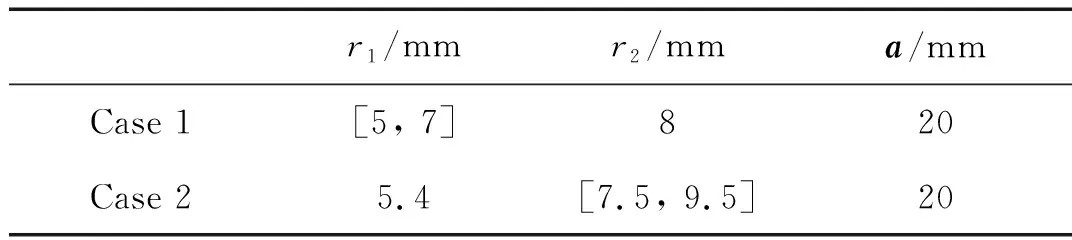
表1 声子晶体几何结构参数Tab.1 Geometrical structure parameter of phononic crystal

由图4(a)可知，当声子晶体内径r1从5 mm逐渐变化到7 mm时，带隙的上下界逐渐向高频带移动，且带隙的绝对宽度逐渐变大。由图4(b)可知，当声子晶体外径r2从7.5 mm逐渐变化到9.5 mm时，带隙上下界逐渐向低频带移动。由此可知，几何结构参数对声子晶体的局域共振带隙有显著影响。通过对几何结构参数的合理调整，可有效优化声子晶体局域共振带隙。因此，本文将几何参数r1和r2作为设计变量对声子晶体进行结构优化。

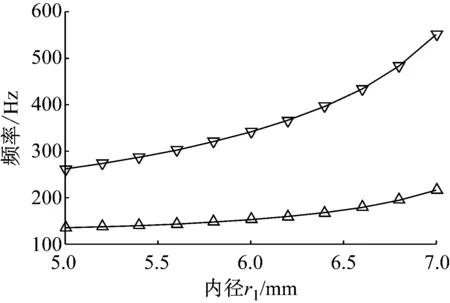
(a) r1

(b) r2图4 结构参数对声子晶体带隙的影响Fig.4 Effects of structural parameters on the band gap of phononic crystals

3.1.2 声子晶体带隙的区间不确定分析

在工程实践中，不确定性广泛而必然地存在着。如果在忽略这些不确定因素的情况下对声子晶体进行优化设计，那么得到的结果往往不可靠。

在区间模型中，不确定参数被定义为变化范围已知的区间变量。梳状夹层声子晶体的橡胶夹层在工程实践中受温度等影响，其材料属性易发生变化。故本文以橡胶夹层的密度ρ和杨氏模量E取为区间变量，如表2所示。

表2 区间变量的变化范围及不确定度Tab.2 The range and uncertainty of interval variables

在区间变量E和ρ的变化范围内等间距地各取10个样本点，共获得10×10=100组样本数据。由图5可知，第三条能带与第四条能带之间形成带隙，带隙下边界频率Fmin和上边界频率Fmax都不是确定的值而是变化的区间。用Fmin2和Fmin1分别表示带隙下边界频率Fmin变化区间的上下限。用Fmax2和Fmax1分别表示带隙上边界频率Fmax变化区间的上下限。表3为Fmin、Fmax和带隙Δf的区间变化范围及不确定度。由表3可以看出，Fmin、Fmax和带隙Δf的不确定度分别为2.6%、2.7%和7.6%。而不确定性参数的不确定度为5%，声子晶体带隙的不确定度比不确定参数的不确定度略大。

由此可知，在受到不确定性参数影响时，声子晶体的带隙不是确定的值，而是变化的区间。而且，声子晶体的带隙的不确定度比不确定性参数中的最大不确定度还大。

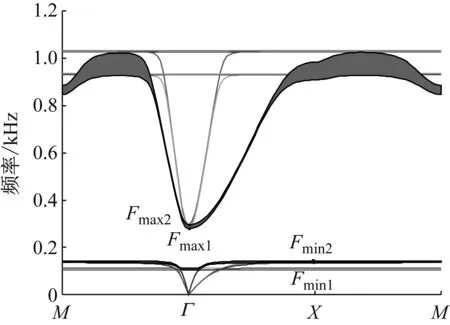
图5 不确定参数对带隙的影响Fig.5 The influence of uncertain parameters on band gap表3 Fmin、Fmax和Δf的变化范围及不确定度Tab.3 The range and uncertainty of Fmin、Fmax and Δf

区间变量变化范围中间值不确定度Fmin /Hz[136.28, 143.41]139.852.6%Fmax /Hz 3[969, 1 071]286.952.7%Δf/Hz[135.92, 158.28]147.107.6%

3.1.3 Chebyshev代理模型精度验证

考虑到声子晶体橡胶夹层易受周围环境因素的影响，橡胶夹层的密度ρ和杨氏模量E均为区间变量，其变化范围分别为[969, 1 071]kg/m3、[0.95×105,1.05×105]Pa。橡胶夹层的剪切模量为γ=0.47。选定内径r1和外径r2为设计变量，其初始为r1=5.4 mm，r2=8.0 mm，其设计范围为[5, 7]mm、[7.5, 9.5]mm。因此，Chebyshev多项式的变量向量x包含设计变量r1和r2以及区间变量ρ和E。采用三阶Chebyshev多项式拟合能带曲线。按照Chebyshev多项式抽样法则，每个变量抽取4个样本点，故在每个波矢k下共抽取44=256个样本点。即采用有限元模型计算256组样本数据，并基于这些样本数据构建每条能带的Chebyshev代理模型。

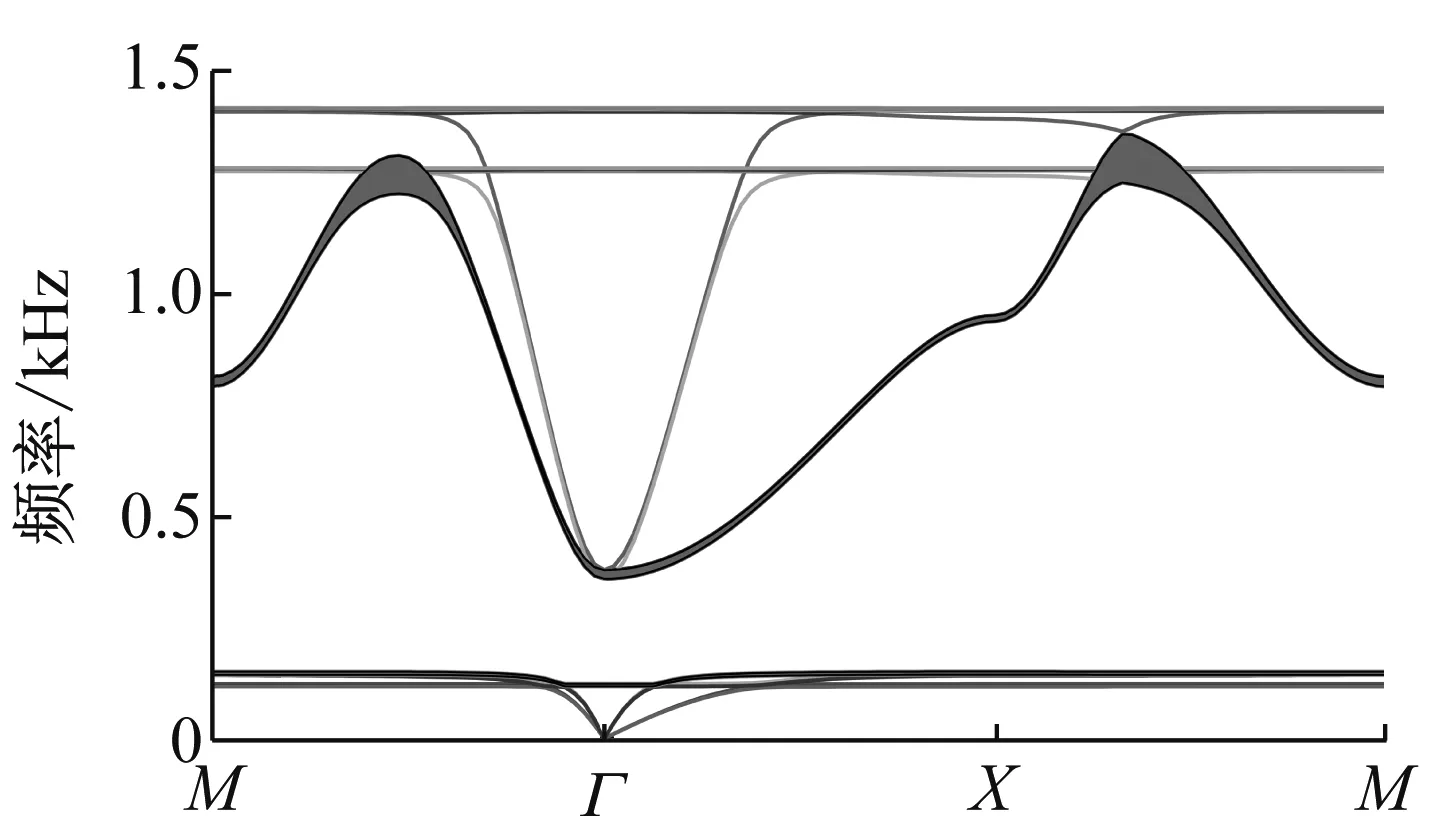
共求解声子晶体的十条能带。由于只有第三条能带与第四条能带之间产生带隙，故只分析第三条、第四条能带的精度以及其产生的带隙精度。图6(a)和图6(b)分别表示r1=6.5 mm和r2=8.5 mm时，基于有限元模型和Chebyshev代理模型的能带图。由图6可以看出，基于Chebyshev代理模型得到的能带与基于有限元模型得到的能带匹配的非常好，Chebyshev代理模型得到的能带上下界与有限元模型得到的能带上下界的误差非常小。

(a)

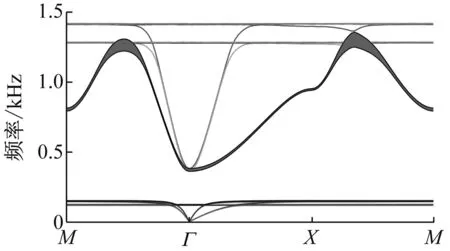
(b)图6 r1=6.5 mm，r2=8.5 mm时有限元方法的能带图及 Chebyshev方法的能带图

Fig.6 The energy band structure based on the finite element method，and the Chebyshev method (r1=6.5 mm，r2=8.5 mm)

有限元模型每分析一次的时间为10 h。若Monte-Carlo法的样本数据为100时，采用有限元模型直接分析声子晶体带隙的变化范围时，其计算成本将达到1 000 h。采用三阶Chebyshev代理模型分析声子晶体带隙的变化范围时，构建Chebyshev代理模型的时间为72.6 h，基于100组样本点分析带隙变化范围的时间为4.3 h。由此可见，若直接采用有限元模型来进行优化，由于极其昂贵的计算成本而将导致优化过程难以实现。本文通过引入Chebyshev代理模型，在保证精度的前提下，极大减少优化时间，提高优化效率。

3.1.4 区间可靠性优化

该声子晶体的区间可靠性优化模型为

max {Fmax,1-Fmin,2}

(21a)

s.t.Fmin2≤200 Hz≤450 Hz≤Fmax 1

E∈[0.95×105, 1.05×105] Pa

ρ∈[969, 1 071] kg/m3

5 mm≤r1≤7 mm

7.5 mm≤r2≤9.5 mm

(21b)

采用遗传算法求解基于Chebyshev代理模型的区间声子晶体的可靠性优化模型，得到了声子晶体最大带隙及其对应的设计变量。种群规模为N=20，交叉概率为Pc=0.7，变异概率为Pm=0.3，最大迭代代数为Gene=60。图7给出了声子晶体最大带隙的收敛过程，图中为最优的个体对应的适应度值(即最大带隙)随进化次数变化的趋势。由图7可知，声子晶体最优带隙在进化代数达到10代时实现收敛。收敛后得到的最优带隙为290.69 Hz。

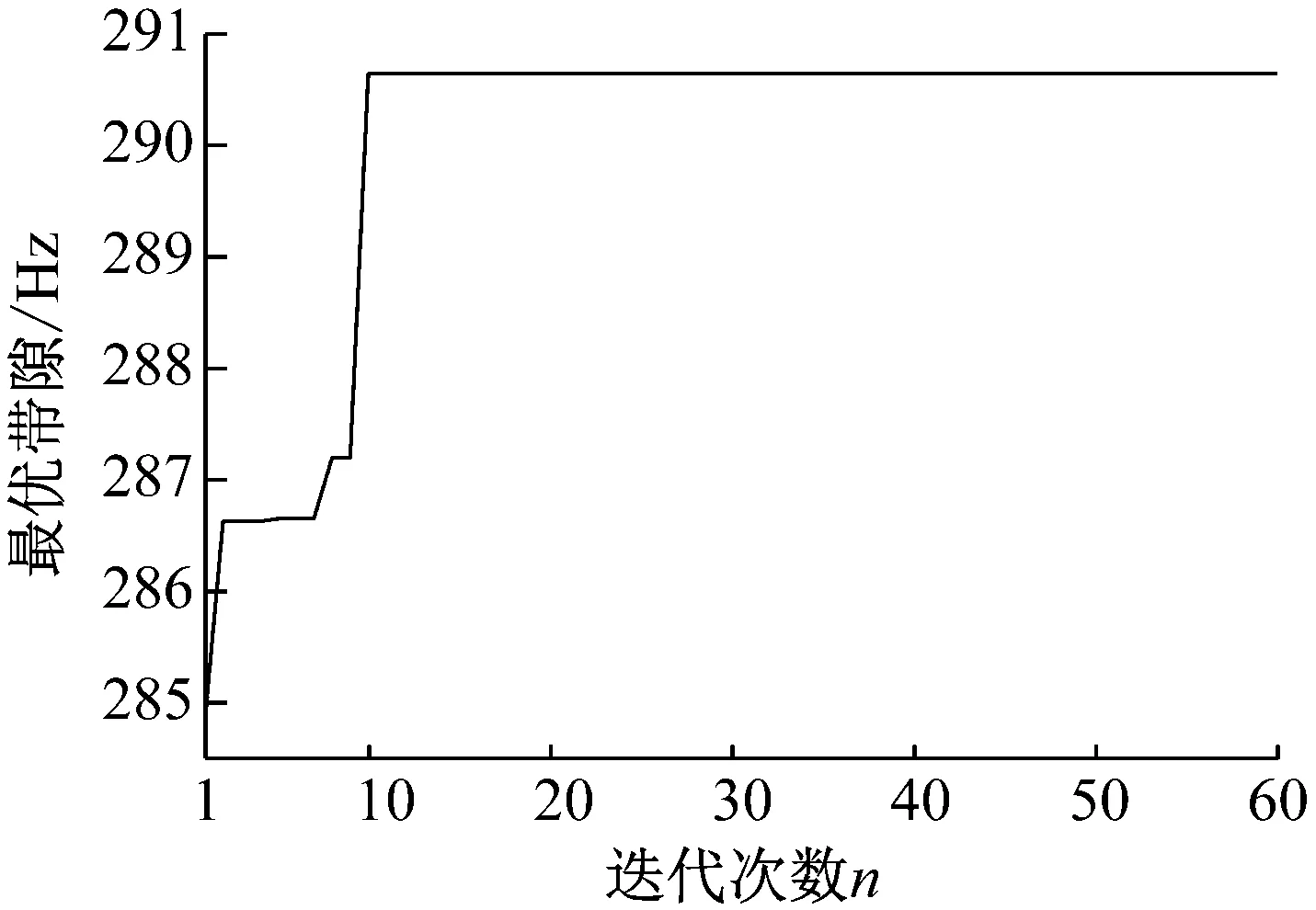
图7 声子晶体的带隙优化收敛图Fig.7 Optimal convergence graph of phononic crystal bandgap

图8为优化前的能带图，设计变量为初始设计变量r1=5.4 mm，r2=8.0 mm。带隙频带为[143.69, 280.26] Hz，带隙宽度为136.57 Hz，且仅频带[200, 280.26] Hz落在期望带隙[200, 450] Hz内。图9为优化后的能带图，优化后的设计变量为r1=6.99 mm，r2=8.13 mm。优化后的带隙频带为[199.85, 490.54] Hz，带隙宽度为290.69 Hz，完全包含期望频带[200, 450] Hz。相对于优化前的带隙，优化后的带隙完全满足约束条件，且带隙宽度从136.57 Hz拓宽到290.69 Hz。

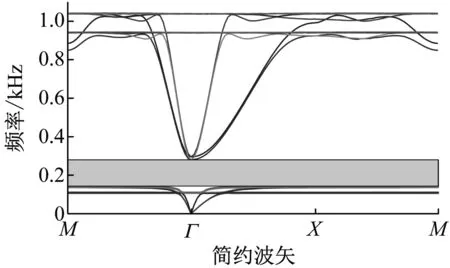
图8 优化前能带图Fig.8 The energy band structure before optimization

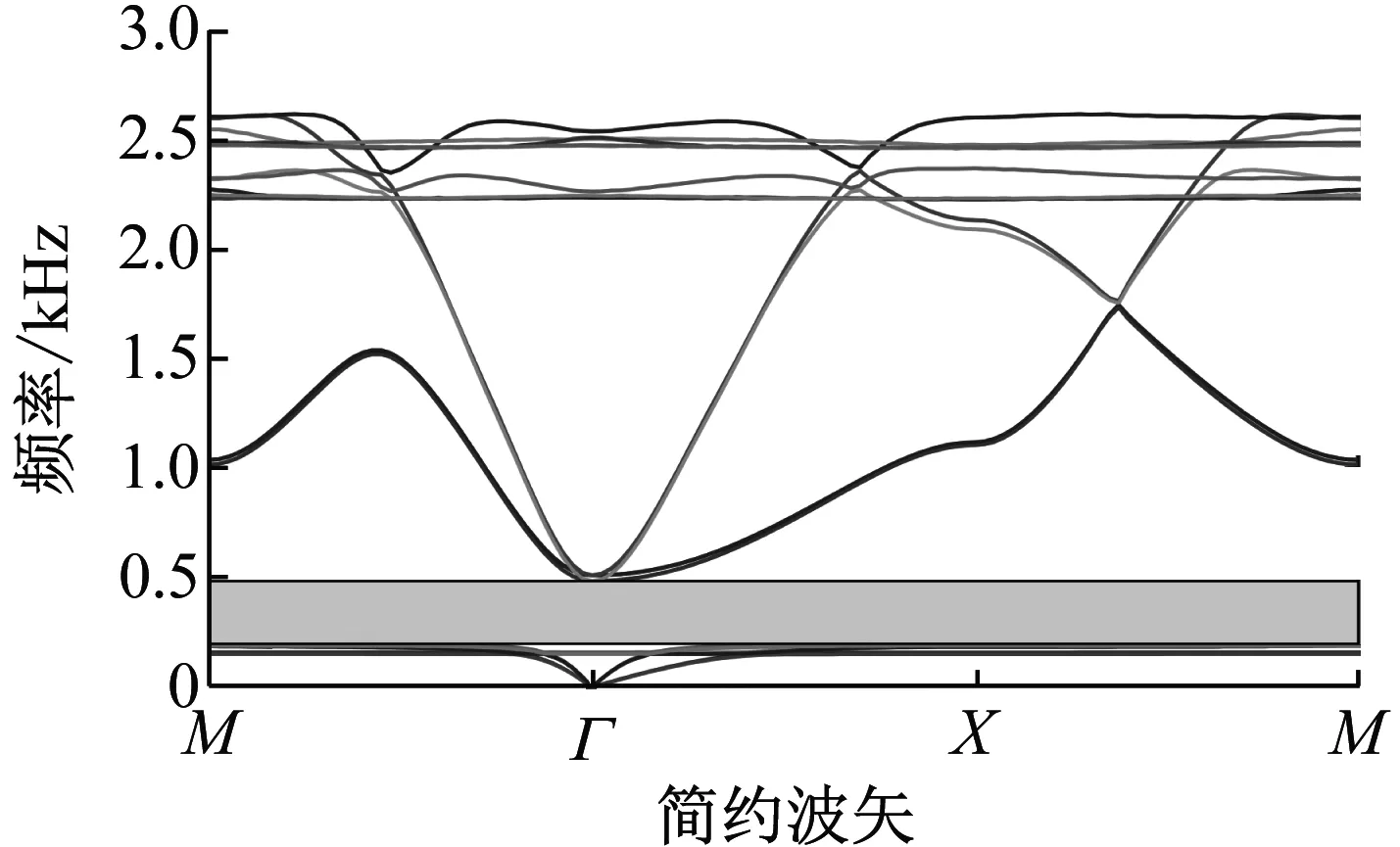
图9 优化后能带图Fig.9 The energy band structure after optimization

4 结 论

本文针对不确定性广泛存在于声子晶体，并严重影响其物理性质这一现状，将区间模型引入声子晶体，描述其模型参数的不确定性。数值分析结果表明，Chebyshev代理模型能高效且较精确地预测区间模型下声子晶体的带隙变化范围。在考虑区间不确定性的条件下，本文以Chebyshev 代理模型为基础构建声子晶体优化模型。优化结果表明，优化后的带隙相对于优化前有大幅度拓宽，且满足期望频带这一约束条件，声子晶体的声音屏蔽性能得到极大地改善。本文所提出的方法在声子晶体的工程实际应用中有广泛的应用前景，不仅极大地提高了不确定条件下声子晶体带隙特性的可靠性，而且通过构建代理模型的方式避免了声子晶体优化设计的巨额计算成本。