表面式永磁同步电机直接转矩控制系统自适应变幅值电压矢量选择策略研究＊

李耀华，任佳越，师浩浩，杨启东，孟祥臻，曲亚飞

（长安大学汽车学院，西安710064）

1 引言

永磁同步电机直接转矩控制技术动态性能好、鲁棒性强，已成为学术界的研究热点[1]-[5]。基于开关表的直接转矩控制技术由转矩和定子磁链幅值误差信号及定子磁链角位置，根据开关表查表选择基本电压矢量来实现对转矩和磁链的增减控制。研究表明：基于开关表的直接转矩控制所选择的电压矢量不能同时始终满足磁链和转矩的控制要求，从而产生不合理转矩脉动，并进一步得出了永磁同步电机直接转矩控制系统电压矢量选择区域[6]-[9]。凡是相角位于选择区域的电压矢量均可实现对磁链和转矩的正确控制。电压矢量幅值越大，电压矢量对转矩和磁链的作用效果也越大。本文基于表面式永磁同步电机直接转矩控制系统电压矢量选择区域，令选择的电压矢量相角为选择区域角平分线，分析了大幅值电压矢量和小幅值电压矢量作用下的表面式永磁同步电机直接转矩控制电压矢量选择系统控制效果，并基于选择两种不同幅值电压矢量的控制效果，给出了一种自适应变幅值电压矢量选择策略。仿真结果表明：本文给出的自适应变幅值电压矢量选择策略在动态时选择幅值较大电压矢量，提高了系统动态性能，在静态时选择幅值较小电压矢量，减小了磁链和转矩脉动。相比较固定幅值电压矢量选择策略，评价函数均值、转矩脉动均方根误差和磁链脉动均方根误差均有所优化。

2 表面式永磁同步电机直接转矩控制电压矢量选择系统

在定子磁链x-y坐标下，表面式永磁同步电机直接转矩控制系统电压矢量选择区域如图1所示[8]。理论上，只要位于选择区域的电压矢量均可满足直接转矩控制系统对磁链和转矩的增减控制要求。

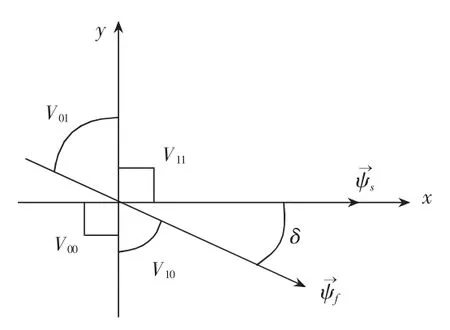
图1 表面式永磁同步电机直接转矩控制系统电压矢量选择区域

表面式永磁同步电机直接转矩控制电压矢量选择系统如图2所示。

图2 表面式永磁同步电机直接转矩控制电压矢量选择系统

基于Matlab/Simulink建立表面式永磁同步直接转矩控制电压矢量选择系统仿真模型。仿真参数如下：系统采样周期为5×10-5s；参考转速为60rpm，参考转矩初始为10N·m，0.3s时阶跃至30N·m，参考定子磁链幅值为0.3Wb。转矩滞环宽度为0.02N·m；定子磁链幅值滞环宽度为0.002Wb。仿真用表面式永磁同步电机参数如表1所示。

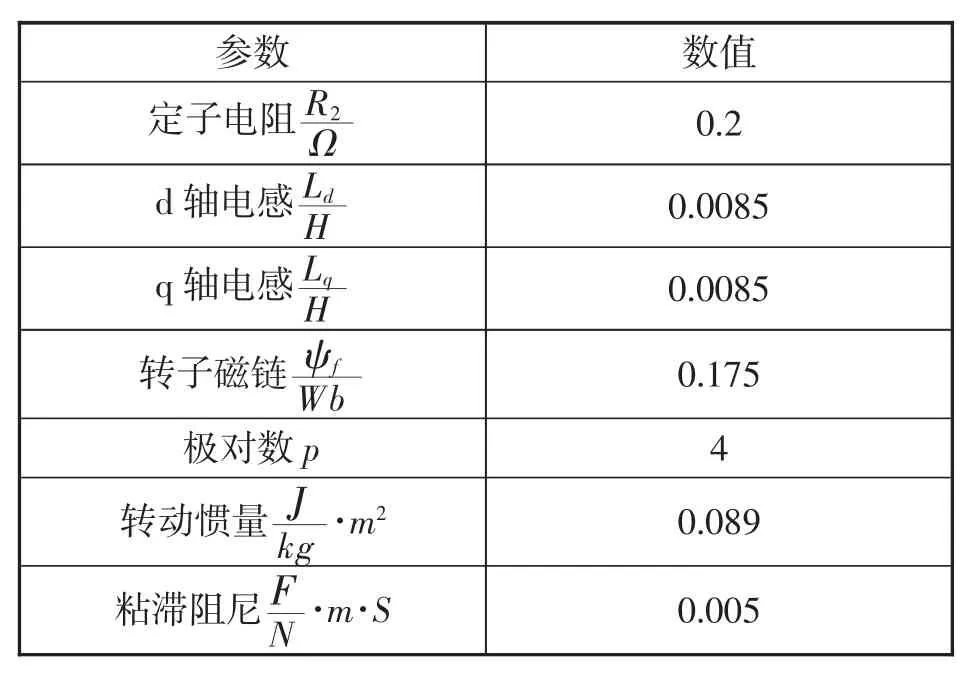
表1 仿真用表面式永磁同步电机参数

图3 电机转速

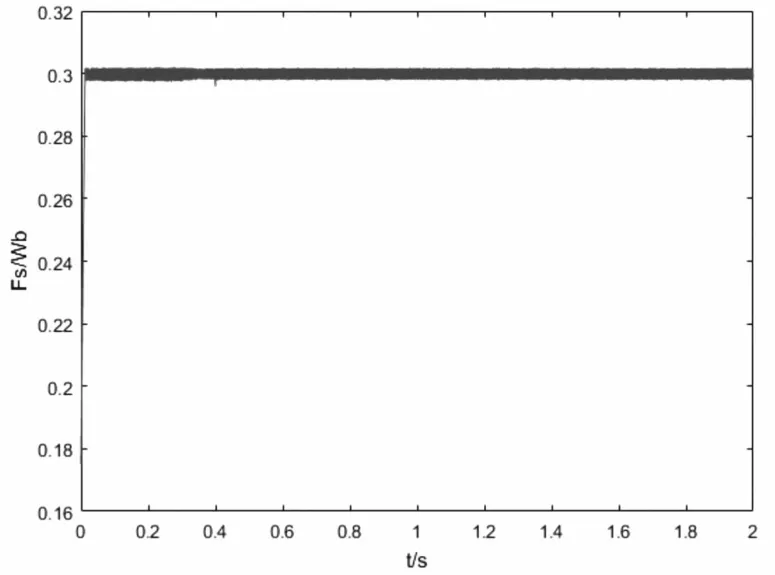
图4 定子磁链幅值

图5 定子磁链幅值误差

图6 电机转矩

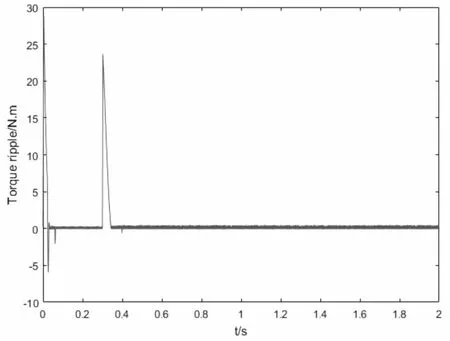
图7 电机转矩误差

由仿真波形可知，由于施加电压矢量幅值较小，转矩响应慢，无法快速跟踪负载转矩变化，从而产生较大的转速跌落和转矩误差。

本文定义评价函数m如式（1）所示，评价函数波形如图8所示。

图8 评价函数波形

本文将评价函数均值、转矩脉动均方根误差和磁链脉动均方根误差作为评价指标，分别如式（2）-（4）所示，其中n为样本数量。

表2 评价函数均值、转矩脉动和磁链脉动均方根误差计算结果

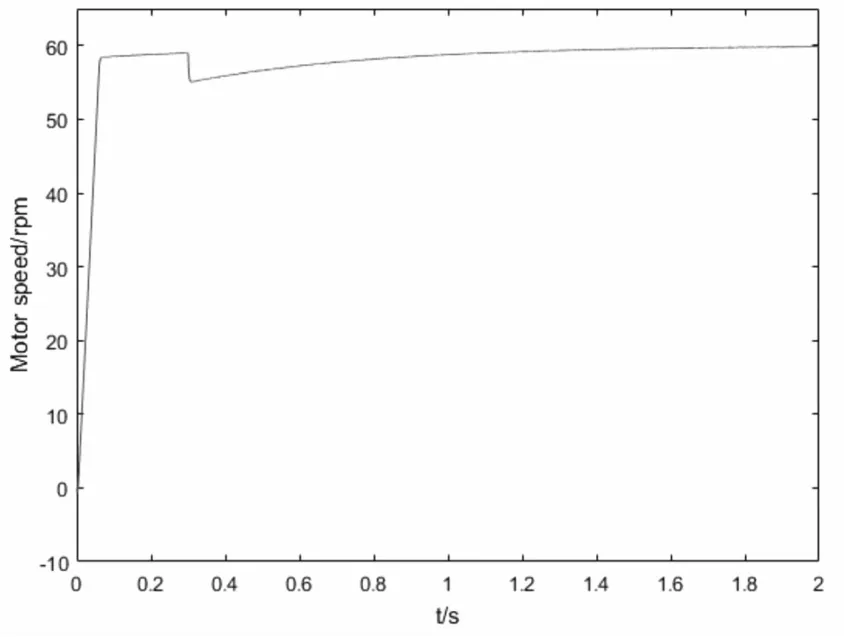
图9 电机转速

图10 定子磁链幅值

图11 定子磁链幅值误差

图12 电机转矩

图13 电机转矩误差

图14 评价函数波形

由仿真波形可知，由于施加电压矢量幅值较大，转矩响应快，能够快速跟踪负载转矩变化，但稳态下磁链和转矩脉动明显增大。

表3 评价函数均值、转矩脉动和磁链脉动均方根误差计算结果

3 自适应变幅值电压矢量选择策略

因此，本文给出一种自适应变幅值电压矢量选择策略。当系统处于动态时，直接转矩控制系统选择幅值为的电压矢量，当系统处于静态时，直接转矩控制系统选择幅值为的电压矢量。当转速、磁链和转矩误差满足式（5），则判定系统处于静态，否则判定系统处于动态。

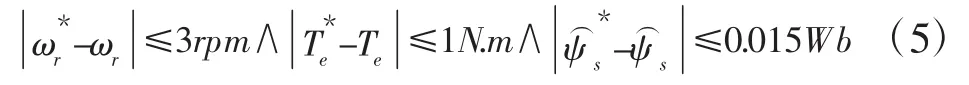
自适应变幅值电压矢量选择策略控制下，电机控制系统施加的电压矢量幅值（图中，1表示幅值为表示幅值为）、电机转速、定子磁链幅值、磁链误差、电机转矩、转矩误差和评价函数波形分别如图15-图21所示。

图15 系统施加的电压矢量幅值

图16 电机转速

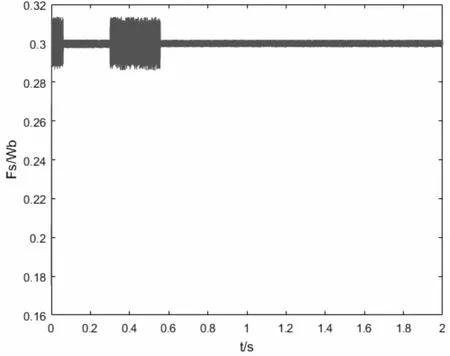
图17 定子磁链幅值

图18 定子磁链幅值误差

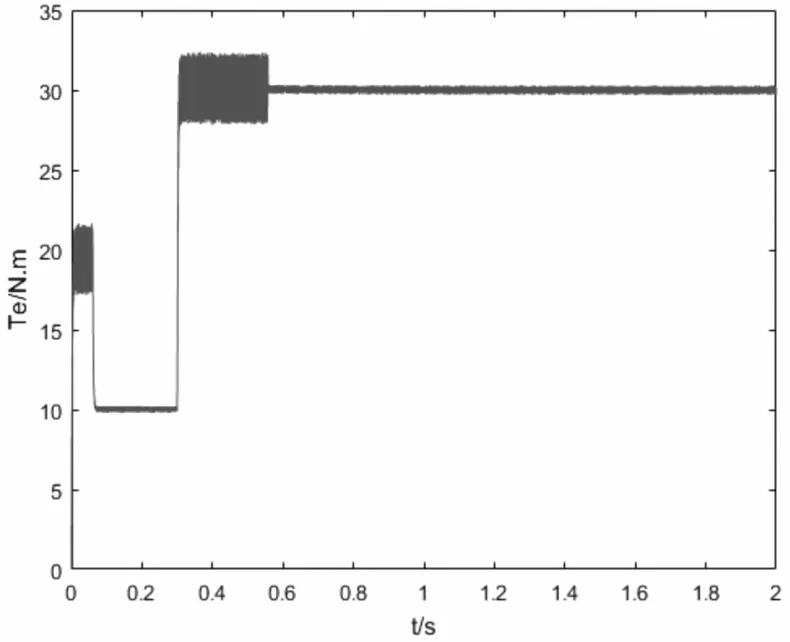
图19 电机转矩

图20 电机转矩误差

图21 评价函数波形

由仿真波形可知，由于自适应变幅值电压矢量选择策略在动态时施加的电压矢量幅值较大，转矩响应快，能够快速跟踪负载转矩变化，在稳态时施加的电压矢量幅值较小，磁链和转矩脉动显著减小。

自适应变幅值电压矢量选择策略控制下，评价函数均值、转矩脉动均方根误差和磁链脉动均方根误差如表4所示。

表4 评价函数均值、转矩脉动和磁链脉动均方根误差计算结果

4 结束语

本文基于表面式永磁同步电机直接转矩控制系统电压矢量选择区域，令选择的电压矢量相角为选择区域角平分线，分析了大幅值电压矢量和小幅值电压矢量作用下的表面式永磁同步电机直接转矩控制电压矢量选择系统控制效果，并基于选择两种不同幅值电压矢量的控制效果，给出了一种自适应变幅值电压矢量选择策略。仿真结果表明：本文给出的自适应变幅值电压矢量选择策略在动态时选择幅值较大电压矢量，提高了系统动态性能，在静态时选择幅值较小电压矢量，减小了磁链和转矩脉动。相比较固定幅值电压矢量选择策略，评价函数均值、转矩脉动均方根误差和磁链脉动均方根误差均有所优化。