降雨条件下水电站弃渣场边坡渗流特性及其稳定性分析

袁 木，秦光辉，张伟锋

（中国电建集团成都勘测设计研究院有限公司施工处，四川 成都 610072）

目前我国水电工程多位于西部深山峡谷地区，由于施工条件差、施工场地匮乏等原因，该区域的工程项目一般将开挖弃渣堆放于沟道内，这种沟道型弃渣场一般具有弃渣量大、堆渣高度较高等特点，渣场一旦失事将对主体工程或环境造成较为严重的影响。因此，弃渣场边坡稳定性是工程设计人员关注的重点问题，特别是在降雨条件下的边坡稳定性更是值得深入研究、分析。

国内许多学者对降雨入渗条件下边坡稳定性进行了研究，并取得一定的成果。贾苍琴、黄茂松等人[1]采用有限元强度折减法方法对水位下降边坡稳定性进行了探讨和分析；王贺、张洁等人[2]提出了考虑时变效应的花岗岩残积土边坡系统可靠度分析方法；向章波、张家铭等人[3]利用Slide软件对降雨条件下的某红层路堑边坡稳定性进行分析；常金源、包含等人[4]建立了降雨入渗条件下浅层滑坡的概念模型，分别推导了降雨前有、无地下水位条件下的边坡安全系数与降雨时间的关系表达式；陈新泽、唐辉明等人[5]利用有限差分软件FLAC3D编制了滑坡体安全系数计算程序；唐栋、李典庆等人[6]对不同初始条件对不同土体边坡稳定性进行研究，重点分析了考虑前期降雨过程对边坡稳定性的影响，并得到一些有益的结论。

以桐子林水电站头道河渣场为研究对象，利用全球著名的加拿大岩土工程设计分析软件GeoStudio，将其中的SEEP/W与SLOPE/W模块进行耦合计算，对水电站弃渣场在降雨条件下的渗流特性及边坡稳定性进行研究分析，重点讨论在持续降雨条件下弃渣场内渗流场的变化及降雨入渗对边坡稳定性产生的影响。

1 非饱和土体边坡稳定性分析理论

1.1 土水特征曲线

土水特征曲线在非饱和土力学中具有重要意义，反映体积含水率与土体基质吸力之间的关系，可用来表征土体的吸水能力。土水特征曲线一般是通过试验确定的，但试验测量法难度较大。Fredlund等[7]对土体孔径分布曲线进行研究，并采用统计分析理论提出土-水特征曲线模型，如下所示：

式中：θ——非饱和土的体积含水量；θs——土体饱和含水量；ψ——土体基质吸力；ψr——残余含水量所对应的基质吸力；a，b，c——模型拟合参数。

1.2 饱和-非饱和渗流基本理论

基于达西定律，对二维饱和-非饱和渗流问题进行分析时，可以假定土体渗流各向同性，即可以得到简化后的饱和-非饱和渗流微分方程：

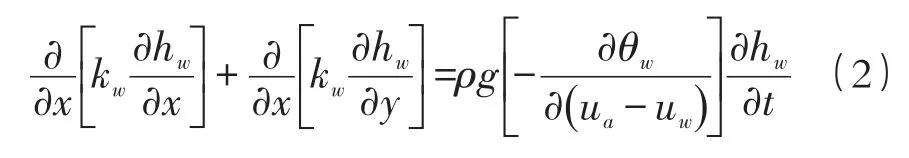
式中：kw——土体的渗透系数，是基质吸力的函数；hw——总水头；ρ——水的密度；g——重力加速度；θw——土体的体积含水率；(ua-uw)——土体的基质吸力。

式中：c′——有效黏聚力；φ′——有效黏聚力；(σ -ua)——为净法向应力；(ua-uw)——为基质吸力；φb——为随基质吸力变化的内摩擦角，通常会随着基质吸力的增大而减小，变化范围为15°～20°，在分析中对其进行了简化处理，假设其为常数[9]。

1.3 非饱和土抗剪强度公式

降雨入渗过程中，边坡非饱和土体抗剪强度受基质吸力的影响，进而影响边坡稳定性。因此，本文采用了Fredlund等[8]提出的非饱和土体的抗剪强度公式：

2 工程实例

2.1 工程概况

桐子林水电站位于攀枝花市盐边县境内，距雅砻江与金沙江交汇口15 km，是雅砻江流域梯级开发的最下游一个电站。头道河渣场位于大坝右岸下游约1.5 km处的头道河沟内，属于沟道型渣场，主要堆存来自引水渠、尾水渠、厂区、左右岸挡水坝、导流工程和交通设施的弃渣，估算堆放渣约为457.5万m3（松方），根据GB 51018-2014《水土保持工程设计规范》，头道河弃渣场级别为3级。渣场典型地质剖面如图1所示。

图1 头道河渣场典型断面地质剖面

2.2 岩土层参数

在饱和-非饱和渗流分析中，基于土体饱和含水率、饱和渗透系数等特征参数，采用SEEP/W模块中自带的Fredlund&Xing土-水特征曲线模型拟合推导得到渣体的土水特征曲线，绘制的曲线如图2，3所示。各岩土层的物理力学参数如表1所示。

图2 渣体渗透系数曲线

图3 渣体土水特征曲线

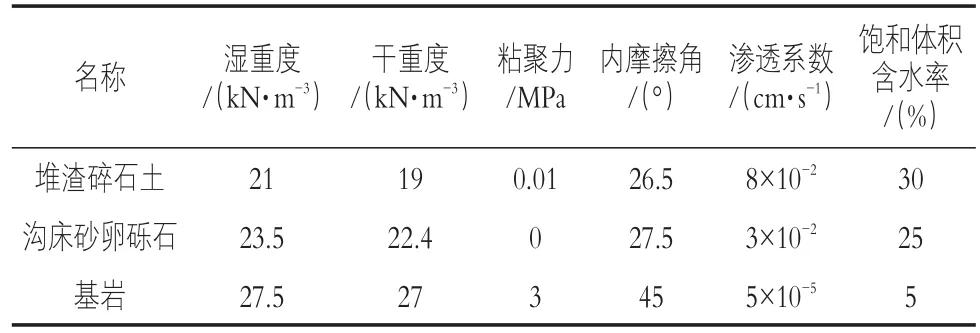
表1 岩土层物理力学参数

2.3 数值模拟

在降雨入渗条件下，非饱和土层中孔隙水压力随之升高、土体重度随之增加，边坡的稳定安全系数则会随之降低。本文首先对渣体进行饱和-非饱和渗流分析，确定降雨入渗条件下的渣体内部孔隙水压力场，然后进行渣体边坡稳定性分析确定安全系数。

数值计算模型：根据头道河渣场现状建立数值计算模型，非饱和渗流计算时采用三角形单元和四边形单元对模型进行有限元网格剖分，共剖分为997个单元，1 057个节点，并在模型表面设置A、B、C3个监测点，如图4所示。

图4 头道河渣场数值计算模型

降雨过程模拟：根据四川省一般降雨强度标准，大雨强度日降雨量为25～50 mm，暴雨强度日降雨量为50～100 mm。本文模拟桐子林水电站头道河渣场遭遇一次暴雨降雨过程，降雨历时7 d，最大日降雨量为60 mm，雨停之后再计算8 d，总共历时15 d，降雨过程如图5所示。

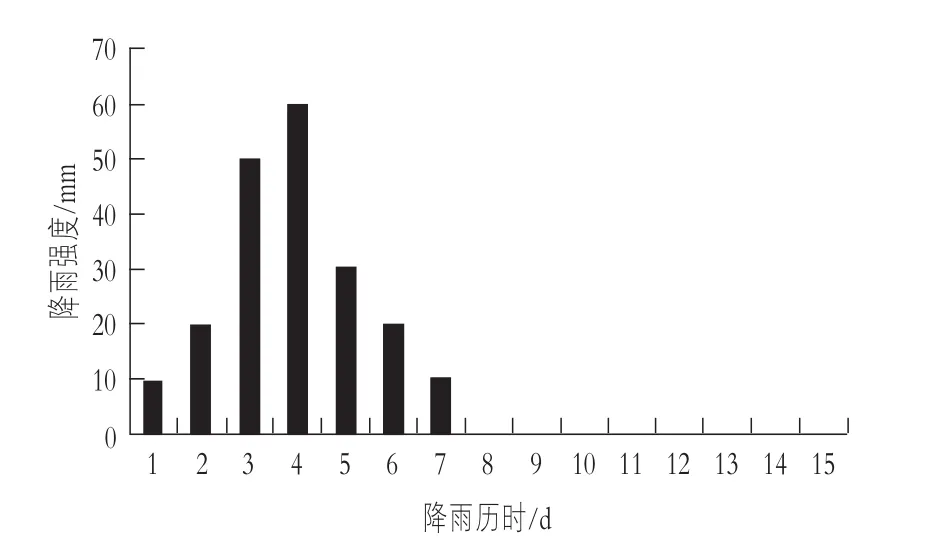
图5 降雨过程模拟

边界条件处理：渣体表面入渗边界取为降雨流量边界；对于模型两侧，地下水位以上取为零流量边界，地下水位以下取为水头边界；模型底面取为零流量边界。

3 计算结果分析

3.1 天然状态分析

天然状态下渣体边坡的孔隙水压力分布情况如图6所示。可以看出，在天然状态下，渣体边坡中的孔隙水压力分布较为均匀，在地下水位线处，孔隙水压力为0，地下水位线以上，孔隙水压力为负值，即处于非饱和状态。正常工况下采用简化Bishop法计算搜索得到弃渣场边坡最危险滑面如图7所示，对应最小稳定性系数为1.422，满足GB 51018-2014《水土保持工程工程设计规范》关于弃渣场抗滑稳定计算值不小于1.25的要求，即渣体处于稳定状态。

图6 天然状态孔隙水压力分布

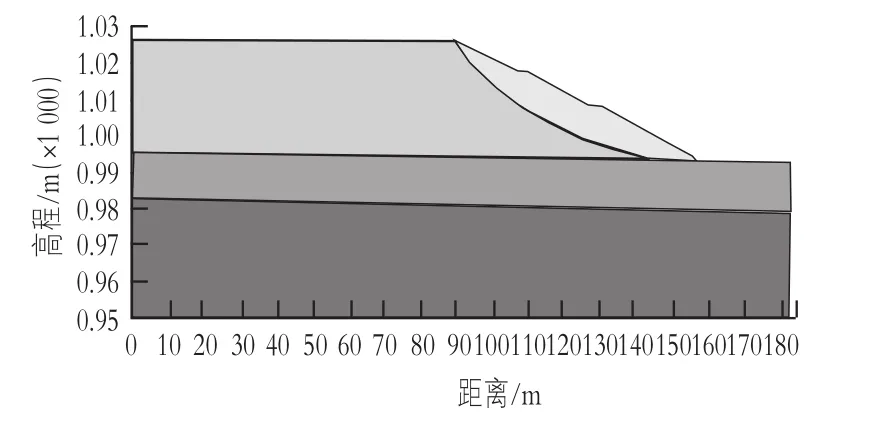
图7 正常工况下边坡稳定安全系数

3.2 降雨条件下渗流特性分析

渣体边坡孔隙水压力分布云图随时间的变化如图8所示。降雨发生时，雨水慢慢渗入渣体内部，渣体内部含水率逐渐增大，并在渣体内部形成新的孔隙水压力等值线，渣体表面附近处孔隙水压力逐渐增大，随着降雨的持续，坡体表面附近孔隙水压力曲线进一步向渣体内部调整，说明雨水慢慢向内部入渗；随着降雨的进一步持续，部分区域孔隙水压力越来越接近于0，直至出现暂态饱和区，在坡体表面形成正的暂态水压力，孔隙水压力变为正值。降雨停止后，渣体表面孔隙水压力逐渐消散，渣体内部由于有上部渗水的补充孔隙水压力仍在缓慢增大。

坡体表面A，B，C监测点的孔隙水压力随时间的变化曲线如图9所示，从图中可以看出：

图8 孔隙水压力随时间变化情况（单位：kPa）

1）在降雨发生的7 d时间内，A，B，C监测点的孔隙水压力随降雨持续而不断增大，A点孔隙水压力由-49.03 kPa增大到-0.97 kPa，B点的孔隙水压力由-49.03 kPa增大到2.17 kPa，C点的孔隙水压力由-49.03 kPa增大到1.10 kPa，在降雨中期，孔隙水压力增长速率较大，后期趋于平缓；

2）B，C两监测点相对A监测点出现了正孔隙水压力，这是因为B监测点位于马道附近，C监测点位于渣脚附近，在降雨过程中该部位容易出现积水，从而形成暂态饱和区，导致正孔隙水压力的出现；

3）降雨停止后，由于渣体表面先失去水分，C监测点的孔隙水压力均随时间而逐渐减小。

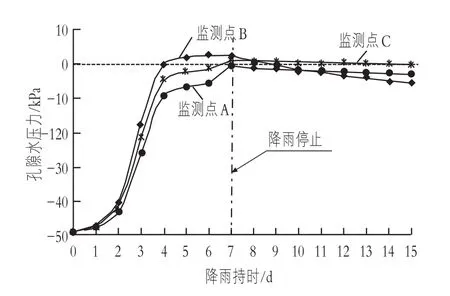
图9 孔隙水压力随时间变化曲线

3.3 边坡稳定性分析

在渗流计算结果的基础上，运用SLOPE/W模块进行边坡稳定性分析，采用简化Bishop法得到边坡安全系数随降雨持时的变化如图10所示，第15 d时简化Bishop法计算边坡稳定安全系数如图11所示。从图中可以看出，弃渣场边坡安全稳定性系数随着降雨时间的增加而逐渐降低，降雨中期安全系数降低较快，雨停之后，边坡稳定系数仍在缓慢降低直至稳定状态，边坡稳定系数从1.422降低至1.394，降低1.97%。

由此可见：

1）降雨发生时，雨水逐渐从渣体表面渗入内部，使得孔隙水压力增大，渣体内含水率增加，基质吸力减小，渣体边坡浅层部位达到饱和状态，使得渣体抗剪强度参数不断降低，导致边坡安全系数不断减小，降雨停止之后边坡内孔隙水压力逐渐恢复至初始状态，边坡安全系数趋于稳定。

2）由于渣体渗透系数一般较大，渗透性较好，雨水可以较快的下渗，降雨期间弃渣场边坡安全稳定系数降低相对不大。

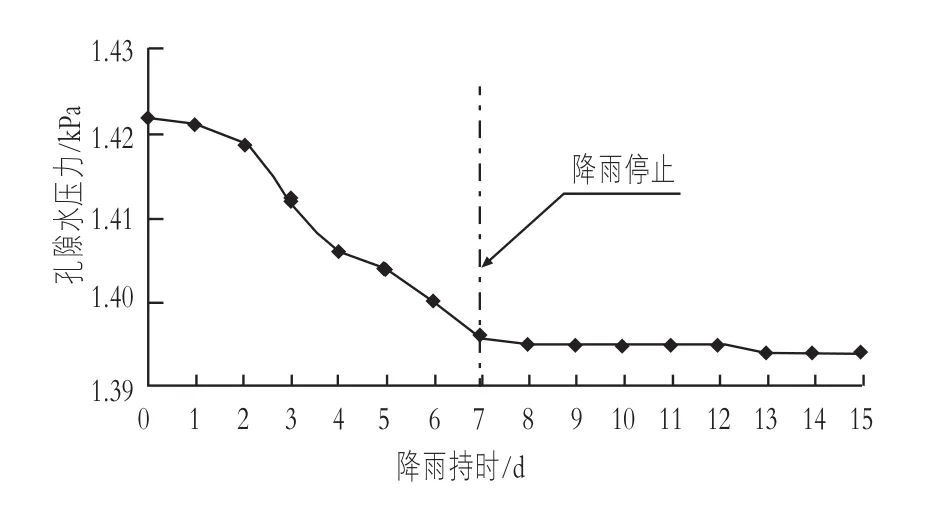
图10 安全稳定性系数变化曲线

图11 第15 d边坡安全稳定系数

在实际工程计算时，对于暴雨工况下的弃渣场边坡稳定计算往往采用参数折减法进行简单计算，本文对两种计算方法进行对比分析，暴雨工况下渣体的物理力学参数作如下折减：重度采用湿重度，内摩擦角由26.5°降低至25°，粘聚力由10 kPa降低至5 kPa，其余参数不变。采用瑞典圆弧法、简化Bishop法、Janbu法分别计算，结果对比如表2所示。从表2中可看出，瑞典圆弧法、简化Bishop法、Janbu法采用参数折减计算出弃渣场边坡安全系数均比采用渗流稳定耦合计算的结果要小，二者差值在9%～10%左右；参数折减条件下采用简化Bishop法计算得到的安全系数为1.256，初始状态下安全稳定性系数为1.422，安全系数降低了11.7%。由此可见，参数折减法计算结果相对偏于保守，渗流稳定计算结果更加贴近于实际。

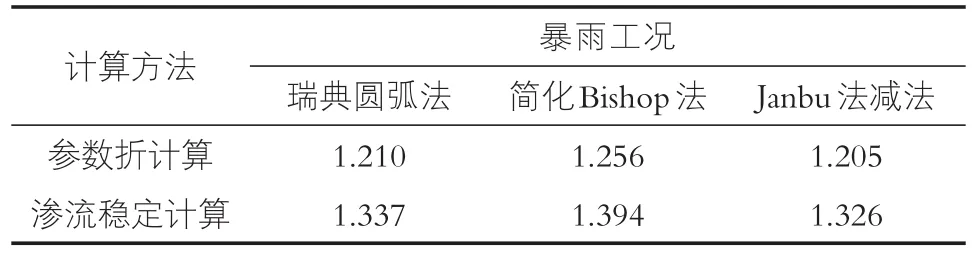
表2 渣体边坡安全稳定性系数计暴雨工况算结果对比

4 结论

基于桐子林水电站头道河渣场，利用SEEP/W与SLOPE/W模块进行耦合计算，对水电站弃渣场在降雨条件下的渗流特性及边坡稳定性进行研究分析，得到以下结论：

1）降雨发生时，渣体内部含水率增加，孔隙水压力逐渐增大，随着降雨的持续，渣体表面部分区域会形成暂态饱和区，在坡体表面形成正的暂态水压力，孔隙水压力变为正值；

2）降雨停止后，渣体表面孔隙水压力逐渐消散，孔隙水压力缓慢减小，渣体内部由于有上部渗水的补充孔隙水压力仍在缓慢增大；

3）降雨入渗导致渣体内部基质吸力减小，渣体抗剪强度参数不断降低，渣体边坡安全稳定系数不断减小，边坡稳定性下降，雨停之后边坡安全系数趋于稳定；

4）相对于采用渗流稳定计算，采用参数折减法计算暴雨工况得到的渣体边坡稳定系数偏小，结果相对偏于保守。