基于改进判别性完整局部二值模式与格分割的织物瑕疵检测方法

赵树志， 狄 岚， 何锐波

(江南大学 数字媒体学院， 江苏 无锡 214122)

目前解决纺织品瑕疵检测问题的方法大致可分为3类：统计学方法、光谱和基于模型的方法[1]。近几年，国内研究人员董蓉等[2]提出了应用积分图的瑕疵检测方法，石美红等[3]提出了基于显著纹理特征的疵点检测方法。针对有图案纺织品，Ngan等提出了基于小波预处理的黄金图像相减方法(WGIS)[4]、布林线指标方法(BB)[5]、正则带方法(RB)[6]、基于基本图案方法(MB)[7]、Elo评分方法(ER)[8]。这其中的一些方法都是基于自动提取子图像基本图案模板。大多数基于模板的方法都是基于预定义和手动确定信息来构建模板。然而，其检测准确率在实际应用中还因为瑕疵的多样性而难以预测。这种固有的局限性制约了根据手动确定模板的方法在实际中的应用。因此本文使用自动模板提取方法(格分割)[9]，以避免手动确定模板所带来的局限性。

确定好模板后，针对模板进行特征提取。在特征提取方法的选择上，基于LBP(局部二值模式)特征的方法运算速度快，并且能有效地描述图像纹理特征，已受到广泛关注和研究。但是LBP算法对噪声敏感，且只考虑了中心像素与邻域像素的差值符号特征，没有考虑差值幅度，丢失了一部分数据信息[10]。为了使LBP特征提取更加充分，Guo等提出了完整局部二值模式(CLBP)算法[11]，CLBP提取的特征比较全面且具有较强的鉴别能力，将其应用在纹理分类中，取得了较高的识别率。但CLBP在提取全面信息的同时，不可避免地提取了干扰信息，不仅增加了时间复杂度，还影响了识别率。

针对传统CLBP所存在的局限性，本文提出一种改进算子，将光滑部分纹理信息考虑进去，提高了纹理识别的精细度；将上述改进的特征提取方法与一种自动格分割方法结合，在解决星形图案和箱形图案瑕疵中有较为出色的检测效果；在比较2种直方图离散程度时，使用双向相对熵散度(KLD)计算方法，提高了直方图间差异度，更有利于衡量离散度。

1 改进disCLBP的瑕疵检测算法实现

1.1 算法描述

本文算法总体分为2部分：训练部分和测试部分。

训练部分：对每张无瑕疵图做格分割处理，并计算得到每个格子(块)的特征直方图，最后求所有格子的平均特征直方图，再将每个格子的特征直方图与平均直方图做KLD散度(相对熵)计算求出散度值，最后得到阈值T。

测试部分：对瑕疵图做格分割处理，计算每张瑕疵图中每个格子的特征直方图并与平均特征直方图做KLD散度计算，将得到的每个值与阈值T做比较，大于阈值T的部分标记为瑕疵。KLD散度计算原理以及阈值T的选取将在下文中介绍。整体算法流程如图1所示。

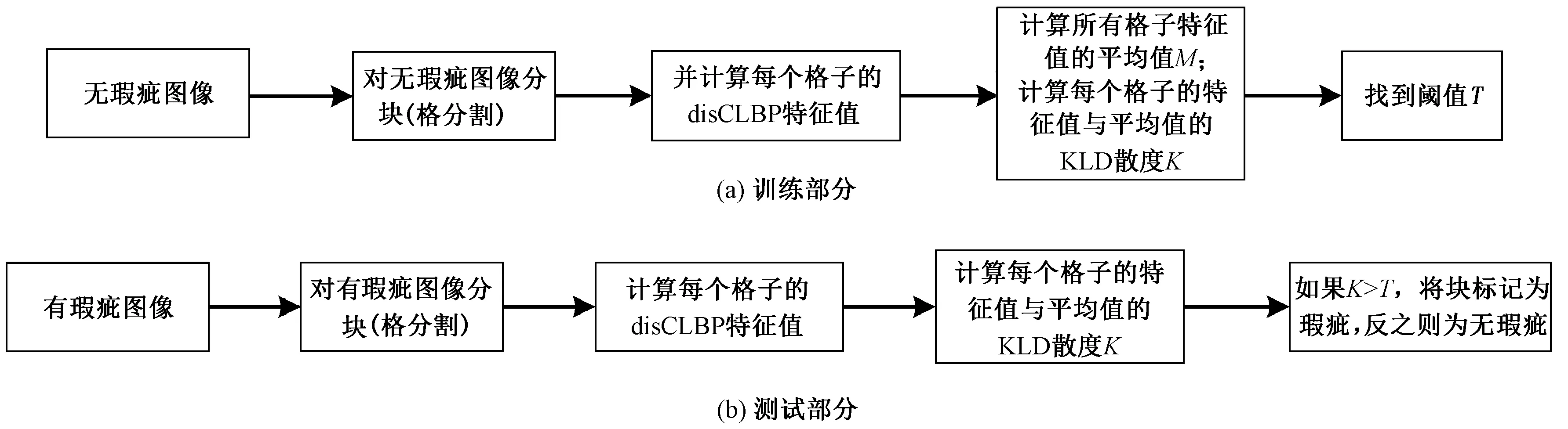
图1 算法流程图Fig.1 Overall block diagram of proposed algorithm. (a) Training part; (b) Testing part

1.2 自动格分割

本文预处理方法使用形态学成分分析(MCA)[13]将原图分成卡通层与纹理层2部分，并且只保留卡通层。下面采用基于自适应K-Means算法[14]的格分割方法对图像分块，具体算法步骤为：

步骤1：用MCA得到输入图像的卡通层Ic并根据阈值二值化产生IIC；

粉丝们pick偶像，就是pick平凡努力的自己；粉丝们pick偶像，某种程度也是在享受反权威的快感。如果说2017年的娱乐关键词是打call，2018年则为pick无疑。pick意为挑选、选择，因选秀节目《偶像练习生》《创造101》的火爆而成功出圈。

步骤2：计算二值图像IIC中各行背景像素数的多重集h，各列背景像素数的多重集v；计算各行背景像素数的多重集h和各列背景像素数的多重集v的峰值hp和vp；

步骤3：分别计算上述中的峰值hp和vp的越区切换算法(HC)轮廓系数，以最大轮廓系数对应的聚类个数初始化 HC 算法，并对峰值hp和vp分别进行聚类，得到的聚类中心构成多重集hc和vc；

步骤4：根据多重集hc和vc计算阈值hmax和vmax，分别计算hp中不小于hmax的峰值所对应行索引的间距和vp中不小于vmax的峰值所对应列索引的间距，计算构成稳定行间距的最长连续行索引的集合Sh以及构成稳定列间距的最长连续列索引的集合Sv；

步骤5：扩展集合Sh和集合Sv以覆盖图像的卡通成分Ic的大部分区域，并计算类格图案的Lh理想行数Lh和理想列数Lv。这样，即可确定出一个标准格的大小。

1.3 特征提取

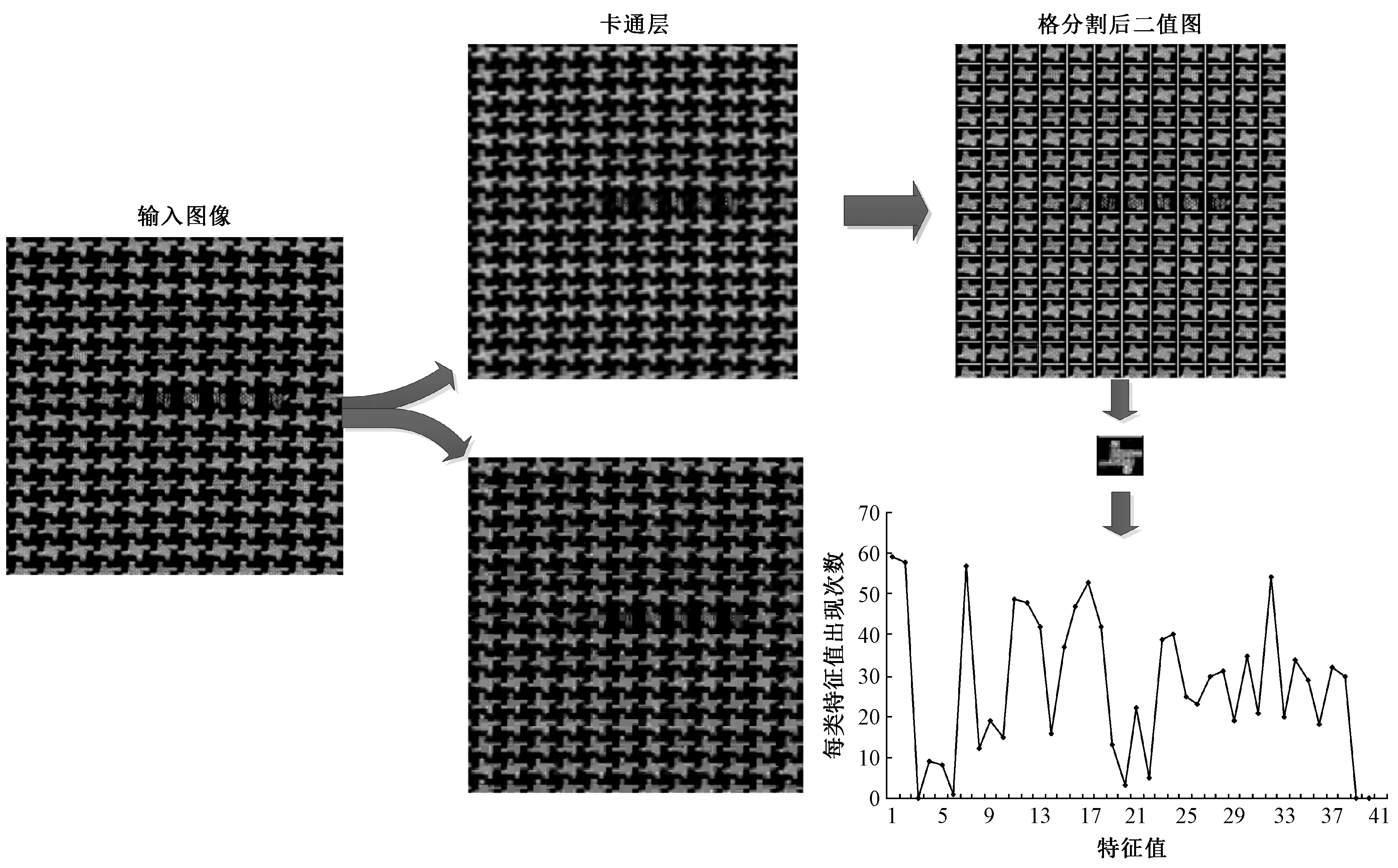
图2 格分割与特征提取Fig.2 Lattice segmentation and feature extraction

本文在传统CLBP的基础上提出了一种改进窗口梯度差异度算子M，通过对比2像素点的灰度差异幅值的均值大小描述局部窗口内灰度梯度差异特征。窗口灰度差异算子S与中心像素点描述算子C与传统CLBP相同。改进算子的计算方法如下：

式中：p为邻域数目；s(x)为算子S、M、C的符号；gc为窗口中心像素点灰度值；gp为中心P邻域各点灰度值；gN为每个窗口内灰度值均值；N为图像划分子窗口个数。本文将改进CLBP算法与判别性CLBP方法结合，将改进disCLBP算法应用到图片特征提取中。上述格分割与特征提取的算法流程图如图2所示。

1.4 相对熵计算及阈值选取

由上述特征提取方法所得直方图的含义是每类特征值在每副图中出现的频率。直方图中，横坐标即为每类特征值，纵坐标为每类特征值出现的次数。KLD散度(相对熵)[15]是一种用来衡量2个概率分布距离的方法(D1,D2)。本文采取一种改进的KLD散度计算方法，与传统方法不同的是，针对特征直方图进行双向KLD计算并求和，计算方法如下：

式中：N为特征向量维数；Pi特征值为i的特征向量在待检测图的特征直方图中出现的频率；Qi为特征值为i的特征向量在平均特征直方图中出现的频率；D为相对熵的值。

在训练部分，通过计算无瑕疵图的每个格子的特征直方图与平均特征直方图的KLD得到一些KLD散度值，在这些散度值中选取阈值的方法为

T=max(Tk)

式中：Tk为所有样本中第k个格子计算得到的散度值。

2 实验结果与分析

图3 星形图断端疵点图像设置不同(R,P)值的疵点检测结果Fig.3 Star broken end defect image and fabric detection results using different (R,P) values.(a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

本文实验使用了香港大学电气和电子工程系工业自动化实验室提供的81幅256像素×256像素的24位彩色纺织品图像[9]，在实验中这些图像被转换为8位的灰度图像。81幅图像包括2种图案：箱形图像和星形图像，其中箱形图像中包括26幅无瑕疵和15幅有瑕疵图像；星形图像中包括25幅无瑕疵和15幅有瑕疵图像。2种图案的有瑕疵图像包括3种瑕疵类型：断端，网纹，和细条纹，所有瑕疵图像都有相同大小的瑕疵基准图，瑕疵基准图为二值图像。其中1表示瑕疵，0表示背景。本文用于比较的算法有传统LBP、WGIS、BB和ER。实验部分所用到的评价指标有：TPR、FPR、PPV、NPV。TPR表示瑕疵基准图中表示瑕疵的像素被算法正确标定为瑕疵的比例，FPR表示瑕疵基准图中表示背景的像素被算法错误标定为瑕疵的比例，PPV表示算法输出的瑕疵基准图中的瑕疵所占比例，NPV表示算法输出的瑕疵基准图中的背景所占比例。对于TPR，PPV和NPV，指标值越大越好，对于FPR则越小越好。

2.1 不同半径和邻域对检测效果的影响

对于disCLBP，设置不同的领域半径R和不同的邻域数目P都会影响检测结果，本文针对这个问题首先进行了对比实验。在实验中，分别设置(R，P)的值分别为(1,8)、(3,8)、(5,12)、(5,16)，针对星形和箱形图进行对比实验，结果如表1、2、图3～8所示。表中黑体表示该行的最优数据。

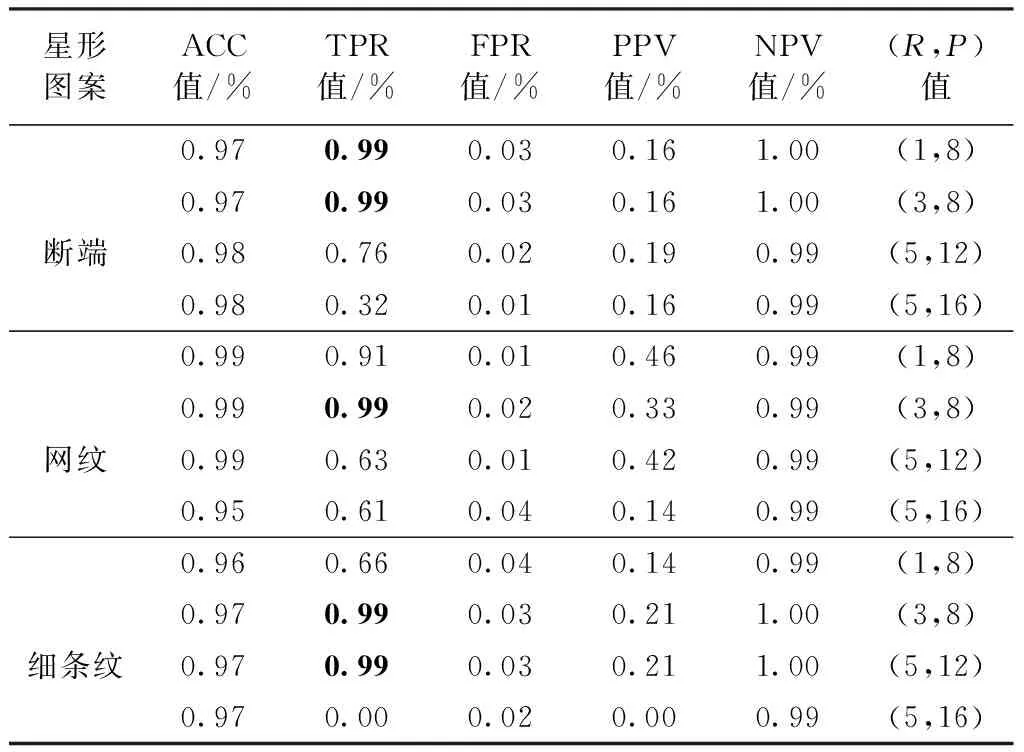
表1 不同(R,P)值对星形图案的检测效果影响Tab.1 Effect of different (R,P) values on star patterns

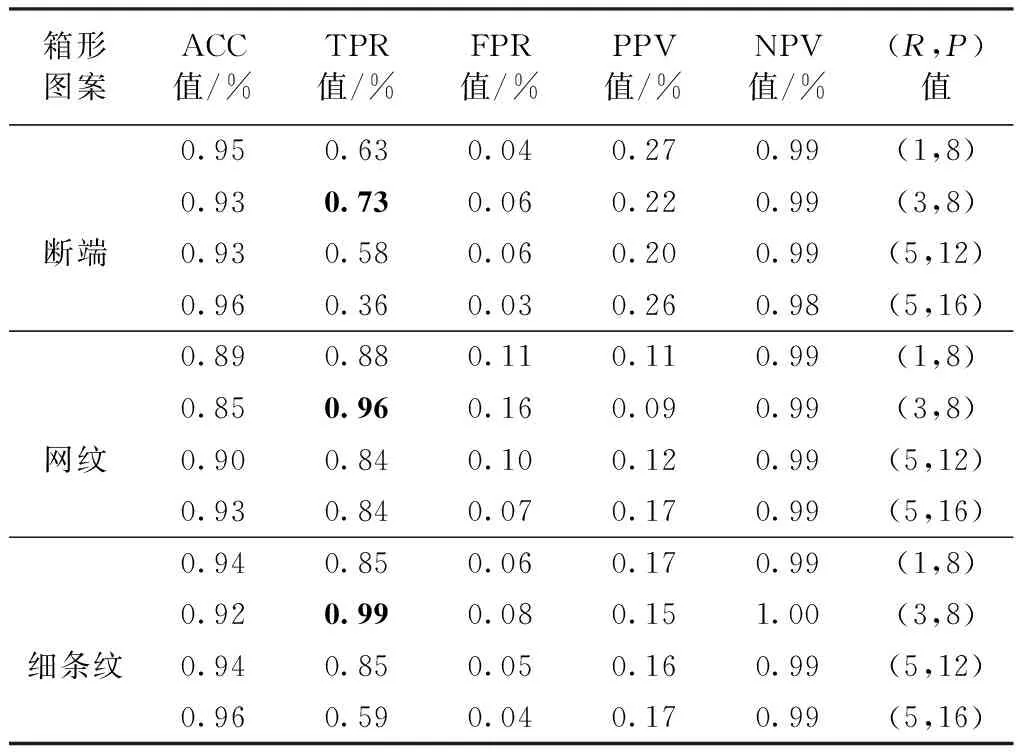
表2 不同(R,P)值对箱形图案的检测效果影响Tab.2 Effect of different (R,P) values on box patterns

图4 星形图网纹疵点图像设置不同(R,P)值的疵点检测结果Fig.4 Star netting multiple defect image and fabric detection results using different (R,P) values.(a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

图5 星形图细条纹疵点图像设置不同(R,P)值的疵点检测结果Fig.5 Star thin bar defect image and fabric detection results using different (R,P) values.(a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

图6 箱形图断端疵点图像设置不同(R,P)值的疵点检测结果Fig.6 Box broken end defect image and fabric detection results using different (R,P) values.(a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

图7 箱形图网纹疵点图像设置不同(R,P)值的疵点检测结果Fig.7 Box netting multiple defect image and fabric detection results using different (R,P) values. (a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

图8 箱形图细条纹疵点图像设置不同(R,P)值的疵点检测结果Fig.8 Box thin bar defect image and fabric detection results using different (R,P) values. (a) Original drawing; (b) (1,8); (c) (3,8); (d) (5,12); (e) (5,16)

2.1.1星形图

对于星形图中的断端类型瑕疵图、网纹类型瑕疵图，在(R，P)值为(1,8)、(3,8)时TPR值差异不大且大于(5,12)、(5,16)时的值。对于细条纹类型瑕疵图，(R，P)值为(3,8)、(5,12)时TPR值达到1.0，(5,16)时TPR值为0。瑕疵检测结果如图 3所示，TPR，FPR，PPV和NPV的平均值(平均值或平均数是算法对特定瑕疵类型的所有图像检测结果的平均值)见表1。

分析图3～5可看出，在网纹类型瑕疵图中，(R,P)值为(5,16)时TPR值虽然有0.61与(5,12)时差异不大但却出现大面积的误检。在细条纹类型瑕疵图中，(R,P)值为(1,8)时出现了小面积的误检，而(R,P)值为(5,16)时TPR值为0且检测结果全部为误检。

2.1.2箱形图

对于箱形图中的断端类型瑕疵图，(R、P)值为(1,8)、(3,8)时的TPR值高于(5,12)和(5,16)时的TPR值，(3,8)时的TPR值最高。对于网纹类型瑕疵图(R,P)值为(3,8)时的TPR值高于其他3种情况，(R,P)值为(5,12)、(5,16)时的TPR值相同且二者都低于(1,8)时的TPR值。对于细条纹类型瑕疵图，(R,P)值为(3,8)时的TPR值最高，达到0.99，(R,P)值为(1,8)和(5,12)时的相同，(R,P)值为(5,16)时的TPR值最低。

图9 星形图断端疵点图像基于不同算法的检测结果Fig.9 Star broken end defect image and fabric detection results using different algorithms. (a) Ground-truth; (b) Method of this paper; (c) LBP; (d) WGIS; (e) BB; (f) RB

分析图6～8中可看出，在网纹类型瑕疵图中，(R,P)值为(1,8)、(3,8)和(5,12)时，存在一定面积的误检，(5,16)时误检率低于其他3种情况。在细条纹类型瑕疵图中，都没有出现误检情况，当(R、P)值设置为(3,8)时，TPR最高。

综上所述，(R,P)值为(3,8)时对2种类型纺织品检测效果最出色，且与相关文献[16]中(R,P)值相同。以下对比实验初始R,P值均为(3,8)。

2.2 本文算法与其他算法对比

将本文算法与传统LBP、WGIS、BB和RB算法进行了对比实验。针对星形图和箱形图的对比实验结果如表3～4、图9～14所示。

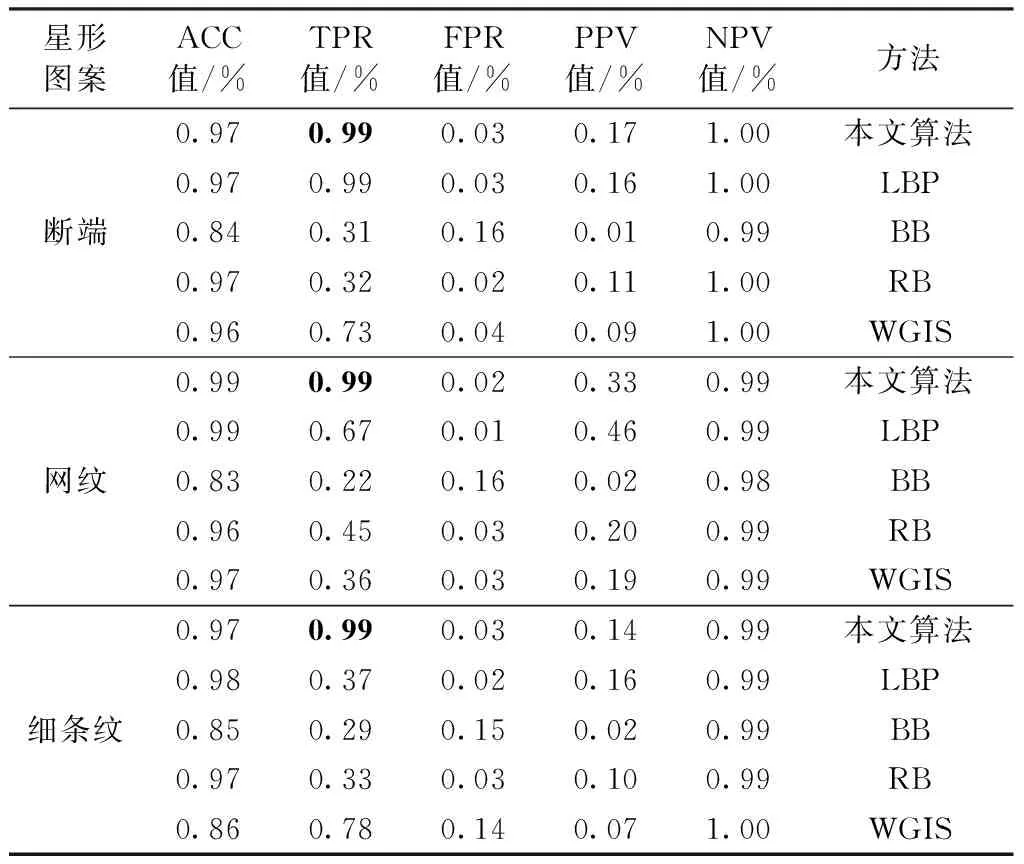
表3 不同算法对星形图案的检测效果对比Tab.3 Test effect of different algorithms on star patterns

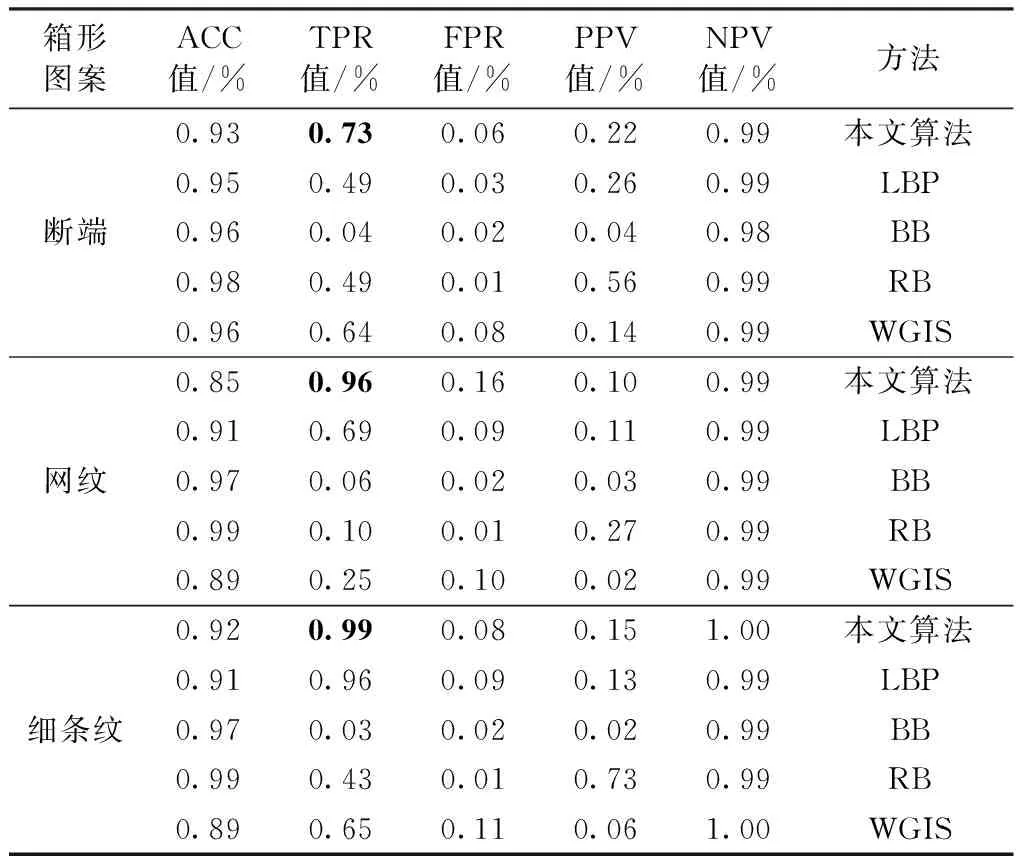
表4 不同算法对箱形图案的检测效果对比Tab.4 Test effect of different algorithms on box patterns

2.2.1星形图分析

图10 星形图网纹疵点图像基于不同算法的检测结果Fig.10 Star netting multiple defect image and fabric detection results using different algorithms. (a) Ground-truth; (b) Method of this paper; (c) LBP; (d) WGIS; (e) BB; (f) RB

图11 星形图细条纹疵点图像基于不同算法的检测结果Fig.11 Star thin bar defect image and fabric detection results using different algorithms. (a) Ground-truth; (b) Method of this paper; (c) LBP; (d) WGIS; (e) BB; (f) RB

图13 箱形图网纹疵点图像基于不同算法的检测结果Fig.13 Box netting multiple defect image and fabric detection results using different algorithms. (a) Ground-truth; (b) Method of this paper; (c) LBP; (d) WGIS; (e) BB; (f) RB

图14 箱形图细条纹疵点图像基于不同算法的检测结果Fig.14 Box thin bar defect image and fabric detection results using different algorithms. (a) Ground-truth; (b) Method of this paper; (c) LBP; (d) WGIS; (e) BB; (f) RB

分析图9～11可看出，在断端瑕疵类型的检测结果中本文算法与传统LBP算法接近且优于其他3种算法，在网纹瑕疵类型的检测结果中本文算法优于其他4种算法，在细条纹瑕疵类型检测结果中本文算法优于其他算法。

表3中数据显示，本文算法在所有3种类型瑕疵中的TPR值均达到最优，FPR值保持稳定， PPV值在断端中达到最优。

2.2.2箱形图分析

分析图12～14可看出，本文算法在断端和细条纹瑕疵类型图中的检测效果均为最优， 在网纹类型瑕疵图中可检测出所有瑕疵，但是存在一定的误检。LBP算法无法检测出所有瑕疵且存在小范围的误检，其他3种算法的检测结果都较差。

由表4数据可知，本文算法在所有3种类型瑕疵中的TPR值均达到最优，NPV值在断端、网纹和细条纹类型瑕疵中达到最优。总体来看，本文方法的查全率整体优于其他算法。

3 结 论

本文提出了一种改进判别性完整局部二值模式(CLBP)织物瑕疵检测方法。提出的改进CLBP算子在一定程度上解决了传统CLBP算法在图像小部分区域变化幅度剧烈或变化幅度平缓时，传统CLBP存在局限性的问题，并结合一种自动格分割算法将图像分块，充分发挥了改进CLBP算子的特征提取效果。本文算法针对星形图和箱形图有较好的检测效果，尤其是针对星形图的检测效果最佳，3种瑕疵类型的TPR值均可达到0.99，且明显优于对比算法的TPR值。针对箱形图的2种瑕疵类型的TPR值均可达到0.95以上，且所有3种的TPR值明显优于对比算法。本文算法的局限性在于可以检测纺织品的类型有限，由于使用的格分割方法无法对数据库中的点形图进行分块，故本文算法无法对点形图进行检测。结合本文方法及其他瑕疵检测方法来克服这些局限性是下一步研究的方向。