《平面向量》解题错因探析及预警教学策略研究

周巧菊 宁文辉

(湖南省常德市鼎城区第一中学 415101)

一、问题的提出

《平面向量》作为高中数学的一块重要内容，它在数学领域应用很广，这决定了它的基础地位.在数学教学中，国内国外有很多教师对向量的教学已有较深的研究.学生在学习平面向量时，常出现的一些典型错题，笔者也有一些研究.

二、平面向量中的典型错题

平面向量是数学中基本和重要概念之一，是沟通代数和几何的重要工具，在实际中也有广泛的应用.通过学生的典型错题，错因探析，形成预警教学策略，这样能让学生正确理解和掌握平向量有关概念，形成严谨的数学思维，提高学生的逻辑分析能力和解决问题能力.

1.平面向量的有关概念

例1 (教材P78第6题(1)、(4)问)判断下列结论是否正确：

(1)若a，b都是单位向量，则a=b.

(2)直角坐标平面上的x轴、y轴都是向量.

易错解答：(1)对；(2)对.

正确解答：(1)错；(2)错.

错因探析向量的概念有两个基本要素：向量的大小(模)与方向.向量的有关概念的理解应抓住这两个基本要素.相等向量是长度相等且方向相同的向量，而单位向量是模等于1个单位的向量，两个单位向量的方向并不一定相同；而x轴、y轴只有方向，没有大小，因而不是向量.这两个小题的错因都是概念理解不到位，属于思维中的大前提错误.

预警教学策略此类概念错误在学生初学时极易出现，在教学时教师注重引导学生对基本概念的理解，形成清晰的判断标准.具体地，可把一些易混淆的概念放在一起让学生自己进行比较辨析，加深学生对基本概念的理解.

例2 下列向量中，可以作为基底的是

A．e1=(0,0),e2=(-1,2)

C．e1=(3,5),e2=(-6,-10)

D．e1=(1,-2),e2=(5,7)

易错解答：选A. 或选B、C.

正确解答：选D.

错因探析平面内两个不共线的向量叫做平面内所有向量的一组基底.对这个命题，学生在学习时只是机械地接受，并没有获得本质上的理解.反之，如果两个向量共线，那无论怎么线性组合都只能表示出与之平行的向量，而不能表示与之不平行的向量.零向量是一个特殊的向量，大小为0，方向可以是任何方向(向量不能没有方向).选A的学生忽视了零向量与任一向量共线的性质，A中的两向量e1,e2是共线向量，不是一组基底；选B或C的学生是对基底的概念并不理解.此题的错误属思维中的大前提错误.

预警教学策略为了避免学生出现此类错误，教师在讲授平面向量的基底这一概念时，要强调两个向量不共线，自然一定是非零向量，可以通过问题的反面设计，让学生理解作为基底的两个向量为什么不能共线；为什么零向量与任何向量共线.

2.平面向量的夹角问题

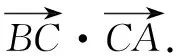
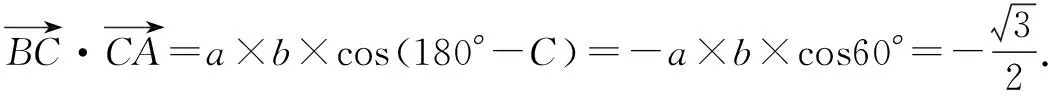
错因探析这类错误发生的频率比较高：有的学生是没有理解两个向量夹角的概念中必需是有相同的起点( 这个小题的错因都是概念理解不到位),因而属于思维中的大前提错误.

3.共线向量的特殊性

例4 (教材P120第1题(7)问) 若平面向量a,b,c两两所成的角相等，且∣a∣=1, ∣b∣=1, ∣c∣=3, 则∣a+b+c∣等于( )

易错解答：错选A. 认为向量a,b,c两两所成的角相等，它们两两的夹角为120°，

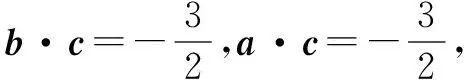
正确解答：因为向量a,b,c两两所成的角相等，

(1)当向量a,b,c共线时，它们两两的夹角为0°，所以，a+b+c=a+b+c=1+1+3=5.

(2)当向量a,b,c不共线时，它们两两的夹角为120°，以下同错解.故应选C.

错因探析在利用题中的条件平面向量a,b,c两两所成的角相等时，学生忽视了向量a,b,c共线同向的情形，考虑问题不严谨，属思维中的小前提错误.

预警教学策略由于学生的思维缺乏严谨性，在考虑问题时常常会对一些显而易见的东西不加注意，三个向量两两所成的角相等，学生确实很容易忽视三个向量共线同向的情形.在数学教学中如何培养学生思维的严谨性的确是数学教师应该引起重视的，就这个错解而言，指导学生发现并纠正错误不难，要有效地预警教学则是很不容易的.要培养学生具有质疑的思维品质：三个向量所成的角两两等，除了成120°的角，还有其他可能吗？即使这样，还是有可能想不到0°，还需要思维的敏锐性.应该说这是一个长期的潜移默化的教学过程.(所以在两个向量的加法和减法的几何意义教学时就需强调，加深理解向量共线的情形)

三、结语

“学生的错误都是有价值的(布鲁若)”.我们老师在课堂上要转变观念，让学生暴露错误，解读学生错误，了解学生错误背后的障碍，错因探析，形成预警教学策略.让错题帮助学生理解和掌握平面向量的基本知识，让错题体现价值.在这一个过程中，巧思妙用，让错题展示魅力，提高了学生分析问题、解决问题的能力，学生数学素养得到提升.