发挥数学题功效 提高学生思维能力

梁秋健

(江苏省吴江高级中学 215200)

数学教学离不开解题，但是数学教学不能沉湎于题海，因此，教师在教学中应该精选习题，发挥每道试题的最大作用，以此减轻学生负担.笔者在教学中，充分发挥数学题的功效，不仅可以引导学生跳出题海，而且还可提高学生的思维，提高教学效益.下面谈谈在教学中提高学生思维能力的几种做法.

一、一题多解，提高学生思维的创造性

有时教师不太重视一题多解，这种做法对学生应试来说，没有错，但是确不利用学生思维能力进一步的发展，事实上，一题多解有利于提高学生探求精神、数学兴趣和独创性思维能力.

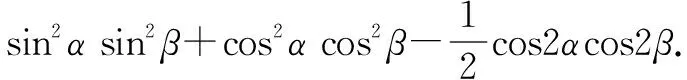
解法一从“角”入手

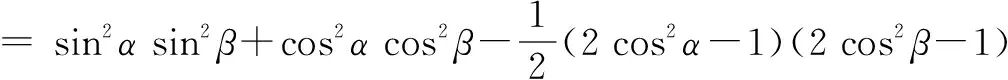
解法二从“名”入手

解法三从“形”入手

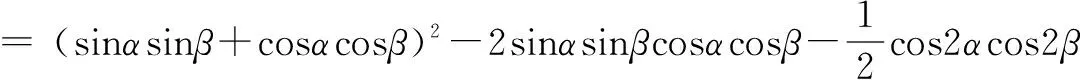
解法四从“幂”入手

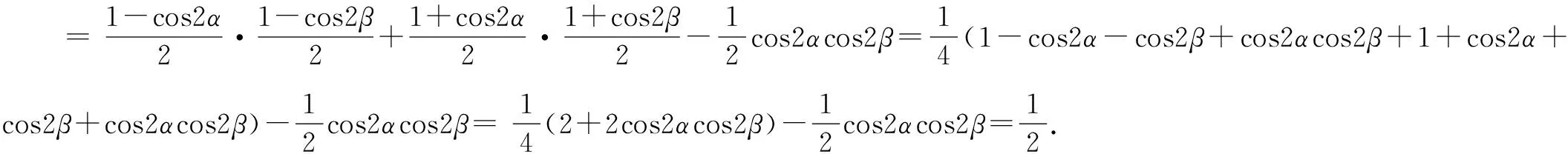
解法1的复角化单角，解法2的同化正弦式，解法3的平方和关系，解法4降次扩角等，都是选择恰当的途径达到目的.因此在习题课教学过程中，可以在发挥学生个性、提高学生独创性思维方面实现突破.

二、一题多变，提高学生思维的灵活性

通过一题多变，如变换已知条件、变换设问、变换解法等途径，可增强学生思维的灵活性，提高解题本领.

例2 已知函数f(x)=x2-2x，x∈[-1,1]，求函数f(x)的最大值和最小值.

变式1 已知函数f(x)=a(x2-2x)，a≠0，x∈[-1,1]，求函数f(x)最大值和最小值.

变式2 已知函数f(x)=x2-2ax，a∈[-1,1]，x∈[-1,1]，求函数f(x)的最小值，用a表示.

变式3 已知函数f(x)=x2-2ax，x∈[-1,1]，求函数f(x)的最值,用a表示.

变式4 已知函数f(x)=ax2-2x，a≠0x∈[-1,1]，求函数f(x)的最小值，用a表示.

这个问题就比较难，结合在解决前四个问题的基础上层层推进，学生会找到解决问题的方法，这样的问题就像是小孩子在果园里摘苹果一样，跳一跳就会有更大的收获.这样必然会调动学生的学习兴趣，使得新旧知识产生化学变化，得到更新的知识，解决更多的问题.

三、一题多问，提高学生思维的发散性

学生拿到一个问题能否及时准确切入，不仅取决于他们的知识储备，更受限于他们思维的广阔性，让他们进行讨论、交流，这样可以启迪思维，开拓解题思路.

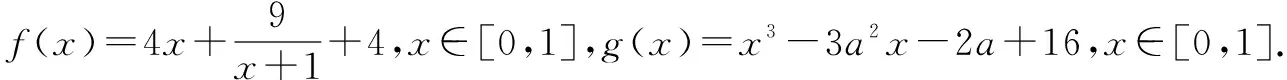
(1)求f(x)与g(x)的值域；

(2)若∀x1∈[0,1],∃x2∈[0,1]，使得g(x2)=f(x1)成立，试求a的取值范围.

分析值域可直接求，本题重在对符号语言的阅读与理解，因此转化成值域或最值处理的典型问题.

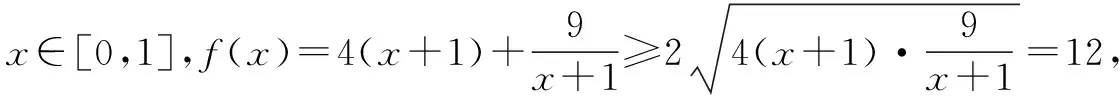
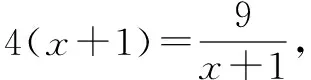
∴f(x)max=max{f(0),f(1)}=13，从而f(x)值域为[12,13].

g′(x)=3x2-3a2=3(x2-a2)≤0，∴g(x)在[0,1]上为减函数，

g(x)min=g(1)=-3a2-2a+17，g(x)max=g(0)=-2a+16.

∴g(x)的值域为[-3a2-2a+17,-2a+16].

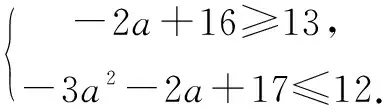
当问题解决后，对该问题还可以进一步追问，如：

(1)若∀x1∈[0,1],∃x2∈[0,1]，使得g(x2)>f(x1)成立，试求a的取值范围.

(2)若∀x1,x2∈[0,1]，使得g(x2)>f(x1)成立，试求a的取值范围.

(3)若∀x∈[0,1]，使得g(x)>f(x)成立，试求a的取值范围.

在教学中除了对上述的经典的高考题进行设问外，现行的苏教版新课标教材中，有一部分例题的“思考”是把例题进行变式训练的，如：苏教版高中数学教材必修2第24页到25页上，在证明了等角定理“如果一个角的两边分别平行于另一个角的两边，并且方向相同，那么这两个角相等”后，提出思考问题：“如果∠BAC和∠B1A1C1的边AB∥A1B1,AC∥A1C1且边AB,A1B1方向相同，而边AC,A1C1方向相反，那么∠BAC和∠B1A1C1之间有何关系？为什么？”

教师在解题教学过程中，不能仅满足于该题会解，要针对教学的重难点，精心设计有层次、有坡度、有广度的问题，要让学生通过一题多问，使思维的广阔性得到不断地发展.

四、正误双解，提高学生思维的批判性

美国教育学家波尼提出了培养学生批判性思维的技巧性策略，在教学中不妨有意识的在学生易犯错的地方，进行正误双解.

例4 若二次函数f(x)的图象关于y轴对称，且1≤f(1)≤2,3≤f(2)≤4，求f(3)的取值范围.

误解∵f(1)=a+c,f(2)=4a+c，

∴1≤a+c≤2,3≤4a+c≤4，

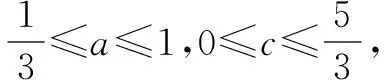
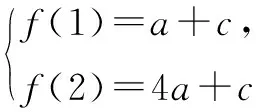
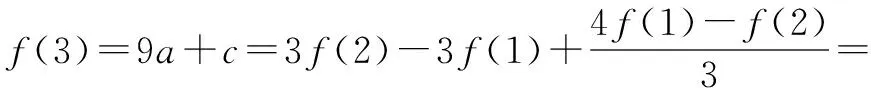
在日常的教学中，要有意识的创造机会让学生发现错误，或者要注意对课本、参考书和教师同学的解法进行反思加工，以此来提高批判思维能力.

总之，数学教师要善于发挥数学题的功效，以小见大，以少胜多，切实培养学生思维能力.除上文所述的方法之外，在解题教学中还应该重视特殊化与一般化思想的熏陶，提高学生思维敏捷性，这样学生必能够获得解决问题一般方法的学习习惯和能力，实现思维升华.