数学思想在解三角形中的精彩绽放
2018-09-22 02:52陈国林
数理化解题研究 2018年22期
蒋 敏 陈国林
(1.四川省南充龙门中学 637200;2.江西省赣南师范大学科技学院 341000)
一、分类讨论思想在解三角形中的应用
例1 已知锐角三角形的边长分别1,3,a,则a的取值范围是
( ).
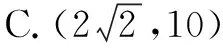

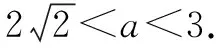
(3)当a=3时,显然此时三角形为锐角三角形,所以选B.
评注由本题题意可知此三角形为锐角三角形,因此必须满足最大边对的角为锐角.因为a与3的大小不定,所以要分类讨论.
变式训练1 在△ABC中,若a2cosAsinB=b2sinAcosB,试判断△ABC的形状.


二、转化与化归思想在解三角形中的应用
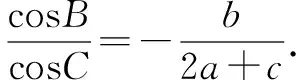
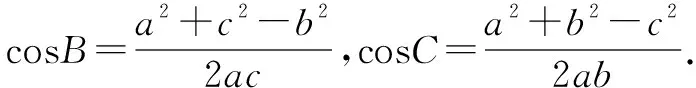

评注本题综合考查了正、余弦定理在转化三角形的边角过程中的作用以及三角变换公式.两种解法诠释了边化角与角化边的解题方法.边化角常常会结合三角恒等变换公式求解;角化边则需利用代数恒等变换求解.
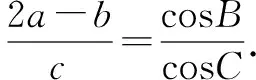
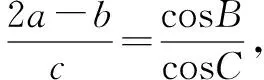
三、函数与方程思想在解三角形中的应用
例3 已知腰长为a的等腰Rt△ABC中,当两个锐角顶点A、B分别在x轴、y轴的正半轴上移动时(C与原点在AB的两侧),求OC的最大值和△AOC面积的最大值.


评注有关最值、取值范围问题常需要运用函数思
想去解决,一般需要通过观察总结进而转化为具体函数的值域和最值问题.
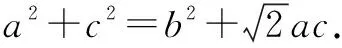
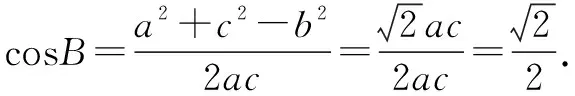
猜你喜欢
中等数学(2021年9期)2021-11-22
中等数学(2021年8期)2021-11-22
语数外学习·初中版(2020年6期)2020-09-10
数学大王·中高年级(2019年2期)2019-01-23
东方教育(2017年14期)2017-09-25
小学生学习指导(中年级)(2017年4期)2017-03-20
中学生天地(B版)(2016年12期)2017-01-05
中国中西医结合皮肤性病学杂志(2016年4期)2016-07-18
课程教育研究·学法教法研究(2016年1期)2016-03-17
西南医科大学学报(2015年1期)2015-08-22

