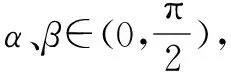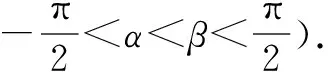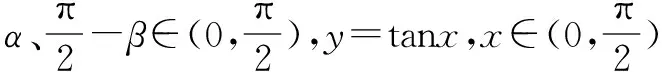挖掘隐含条件 巧解三角问题
张艺琼
(河北省石家庄二中实验学校 050000)
在解三角问题时,应善于挖掘题目中的隐含条件,采用联想、构建等诸多方式,将隐蔽问题转化为熟知而明朗的问题,从而开辟出解题通道,获得新颖别致而富于创造性的巧妙解法.现将学习中的体会整理如下.
一、挖掘出锐角三角形中,两角之和的范围
例1 在锐角△ABC中,比较sinA+sinB+sinC与cosA+cosB+cosC的大小.
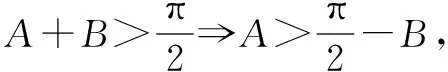
同理有sinB>cosC,sinC>cosA,三式相加,得
sinA+sinB+sinC>cosA+cosB+cosC.
二、转化为三角形中,边角的大小关系
例2 在△ABC中,设条件p:sinA>sinB,条件q:A>B,判断p是q的什么条件.
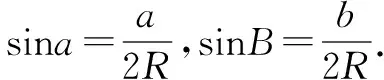
三、构造出直角三角形中的边角关系
例3 已知锐角α、β满足条件7sinα=5sinβ,7cosα+5cosβ=7,求α+2β的值.
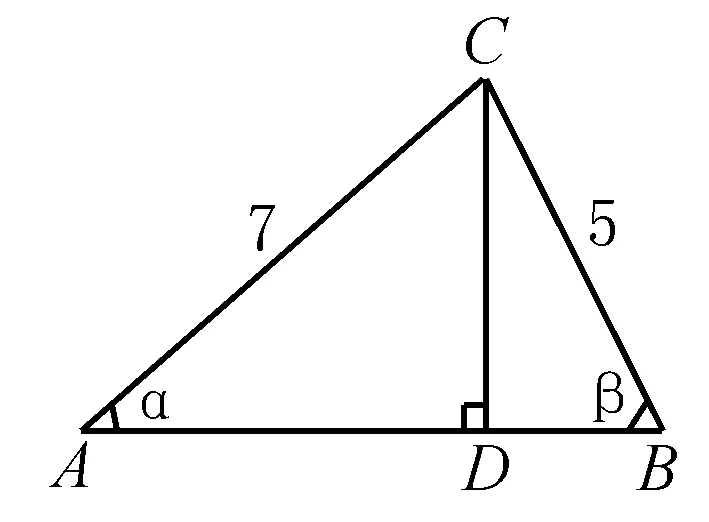
解把7sinα、5sinβ与7cosα、5cosβ视为直角三角形中的两个直角三角形的直角边,如图1.
构造锐角△ABC,CD是高,其中AC=7,BC=5,∠A=α,∠B=β.由直角三角形中的边角关系知
7sinα=CD=5sinβ,7sinα=AD,5sinβ=DB.
AB=AD+DB=7sinα+5sinβ=7,可知AB=AC,故∠ACB=∠B=β.由三角形内角和知A+B+C=π,即α+β+β=π,从而α+2β=π.
四、利用|sinx|≤1,|cos|x≤1.
例4 已知α、β均为锐角,且sin(α+β)=2sinα,求证α<β.
证明由α、β是锐角,知0 解将原式去分母,整理成2sinx-ycosx=y+1. 根据辅助角公式可得 例6 求cos271°+cos71°cos49°+cos249°的值. 解记a=cos271°+cos71°cos49°+cos249°, 构造对偶式b=sin271°+sin71°sin49°+sin249°. 则a+b=1+cos(71°-49°)+1=2+cos22°①, a-b=cos142°+cos(71°+49°)+cos98° 解f(-x)=ln(secx+tanx),与f(x)的解析式对照,发现隐含公式,f(-x)+f(x)=ln(sec2x-tan2x)=ln1=0,从而f(-x)=-f(x),所以f(x)是奇函数. 分析将已知式去分母,并化为关于α+β、α-β的三角式. 证明已知式去分母,可得到sin2α+sin2β=4sinαsinβ. 右边积化和差,可写成 sin[(α+β)+(α-β)]+sin[(α+β)+(α-β)]=-2[cos(α+β)-cos(α-β)], 化为sin(α+β)cos(α-β)=cos(α-β)-cos(α+β), 另一方面,
五、呈现辅助角公式
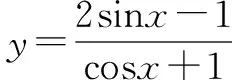
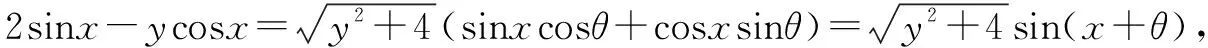
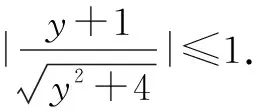

六、联想正弦、余弦的平方和、平方差公式


七、应用隐含公式sec2x-tan2x=1
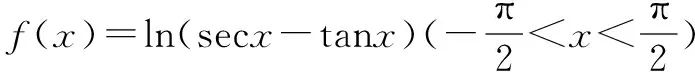
八、引入相应函数
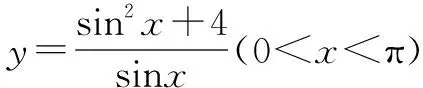
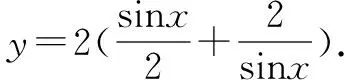
九、采用夹逼法