向量问题中的最值学习札记

武增明

(云南省玉溪第一中学 653100)

一、从建立平面直角坐标系入手

因为向量可以用坐标表示，所以通过建立平面直角坐标系，把向量转化为坐标，就把向量问题转化为代数或三角问题，接下来的工作就是去解决代数或三角问题.

1.从建立平面直角坐标系入手，把问题转化为三角函数最值问题

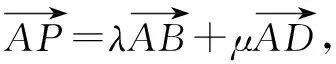
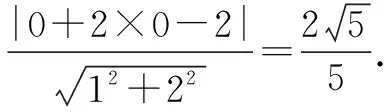
评注(1)建立平面直角坐标系，将点A，B，C，D，P的坐标表示出来是快速解决此题的关键.(2)以点A或点B或点D为原点建立平面直角坐标系的计算量比以点C为原点建立平面直角坐标系的计算量稍大一些.(3)由上述解法知，λ+μ有最小值1.

2.从建立平面直角坐标系入手，把问题转化为二元函数最值问题

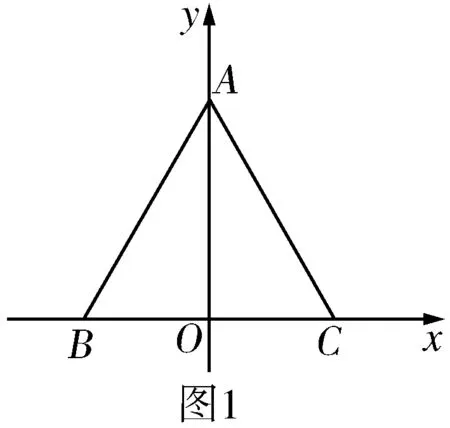
评注对于平面向量中涉及求数量积的最值(取值范围)问题，建立平面直角坐标系，可使问题变得简单.

二、从向量的基本定义入手

从向量的基本定义、基本运算法则、基本公式、线性运算、坐标运算及向量的几何意义入手，把向量问题转化为代数或三角函数问题.

1.从向量的基本定义入手，利用向量绝对值三角不等式及基本不等式解决问题

例3 (2017年高考浙江卷·文15理15)已知向量a，b满足|a|=1，|b|=2，则|a+b|+|a-b|的最小值是 ，最大值是 .

解析∵|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|=2，且|a+b|+|a-b|≥|(a+b)-(a-b)|=2|b|=4，∴|a+b|+|a-b|≥4，当且仅当a+b与a-b反向时取等号，此时|a+b|+|a-b|取最小值4.

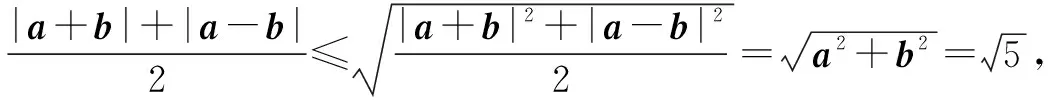
当且仅当|a+b|=|a-b|时取等号，此时a·b=0.

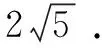
2.从向量的基本运算入手，把问题转化为函数最值问题

例4 上述例3.

解析设b=(2，0)，a=(x，y)，则x2+y2=1.

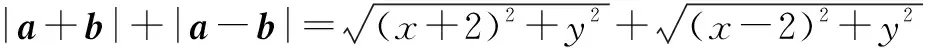
∵ 0≤x2≤1，

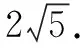
当x2=1，即a∥b时，|a+b|+|a-b|有最小值4.

评注设a=(cosθ，sinθ)也可以.

3.从向量的坐标形式入手，把问题转化为函数的最值问题

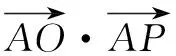
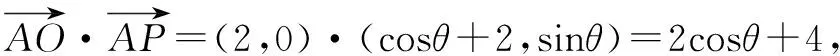
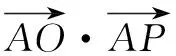
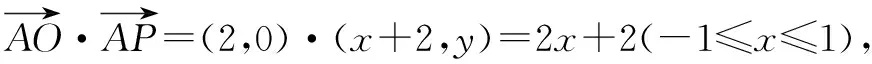
三、从图形入手，通过图形的直观判断解决最值问题

向量是沟通代数与几何的重要工具，它集数与形于一身，既有代数的抽象性，又有几何的直观性，因而向量是几何研究的一个有力工具.恰当地将抽象的向量语言转化为图形语言，通过图形的直观性去观察、分析，就可以寻找到解决问题的突破口，这种方法称为图解法，这种思路是破解向量背景下最值问题的一种有效途径.

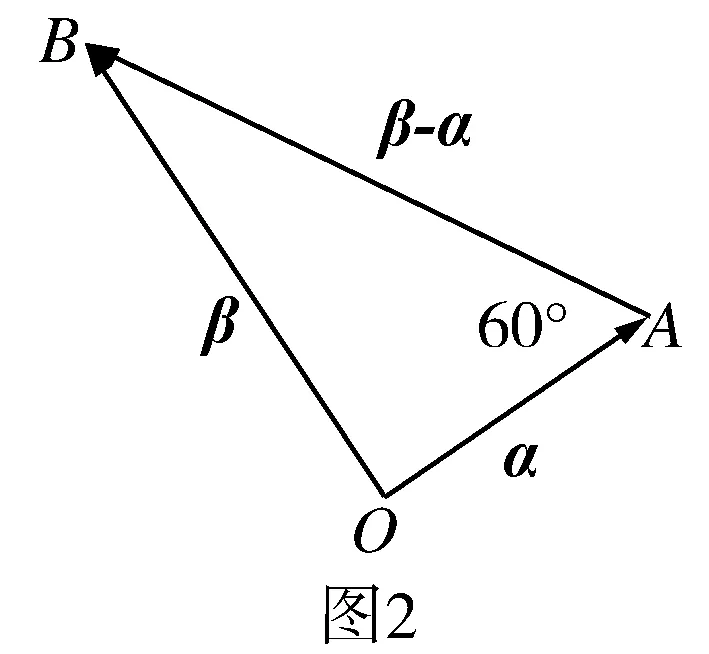
例6 (2010年高考浙江卷·理16)已知平面向量α、β(α≠0，α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的最大值是 .

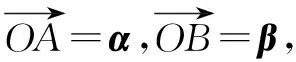
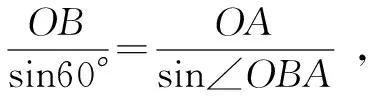
评注(1)向量是既有大小又有方向的量，具有代数和几何的双重身份.本题由β-α联想到向量减法的几何意义，恰当地将条件转化为图形语言，将向量问题转化为三角问题，借助解三角形的方法来处理，有效地建立了向量与三角的联系，使问题变得清晰明了.(2)此题解法较多(参见文[3])，笔者认为上述解法直观、简捷，容易被学生接受，值得我们一线教师重视.

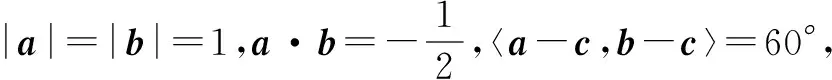
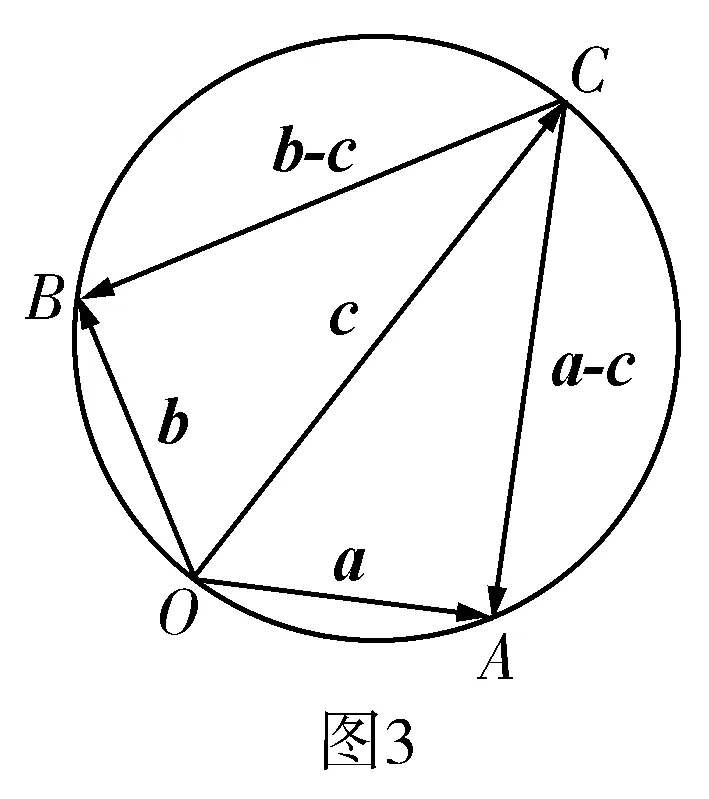
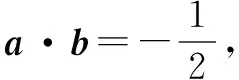
又由〈a-c，b-c〉=60°，知∠ACB=60°.

因此∠AOB与∠ACB互补，所以O、A、C、B四点共圆，根据图形可得当OC为该圆的直径时，则|c|为最大.

此时，∠OAC=∠OBC=90°，又OA=OB=1，所以Rt△OAC≌Rt△OBC，得∠AOC=∠BOC=60°.

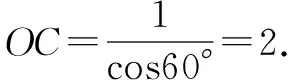
故选A.

评注(1)该题的“原型”是2008年高考浙江卷理科第9题：已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是( ).

将两者进行比较，发现除了角度的设置不一样，其余几乎一致.这也提醒我们要多研究高考题，从高考题的求解中去总结思想方法，方能以不变应万变，进而提高自己的解题能力.(2)此题被考生公认为当年高考难题，难倒了许多考生.究其原因，是没有想到要从图形角度思考，或者作出符合题意的图形后，没有想到四点共圆.此题可以说确实难，如果没有想到上述解法，用其它方法很难求解，甚至解不出来.