电梯运行模式的分析及优化设计

罗昱颖 泸州天立国际学校

引言：随着社会经济的发展，高层建筑不断涌现，而电梯是高层建筑中必不可少的交通设备高效，因此高效的电梯运行模式显得尤为重要。对于一些上班族和学生党来说，既想要睡懒觉，又想上班、上学不迟到，那么从家到公司、学校所需等待和乘坐电梯的时间就决定了你是否能准时搭上公交车，是否能躲过迟到的魔爪。本文通过对我们生活中最常采用的随机运行模式和奇偶层运行模式进行建模分析找到电梯运行模式的优化方案。

1 模型假设及参量描述

1.1 电梯运行规则假设

（1）楼层数为（F+1）（F≥1）

（2）电梯上行时均在第一层达到满载，最大客容量为P，下行时不再装载客人

（3）每位乘客在各层下电梯的概率相等，且相互独立

（4）电梯需要向各层运送的乘客数为c，设各层人数相等，即电梯需要运送的总乘客数为（F+1）c

1.2 电梯运行时间假设

（1）不考虑电梯启动与制动时的加速和减速过程，即电梯已匀速v运行

（2）电梯运行时在相邻两层楼间所经时间为t1

（3）设电梯在每层停留以供乘客出入的时间与乘客量无关，为时间t2（该时间已包含电梯停靠时门的打开和关闭所需时间）

（4）设电梯完成一次全部输送所需的总时间T

将所用变量列为表一：

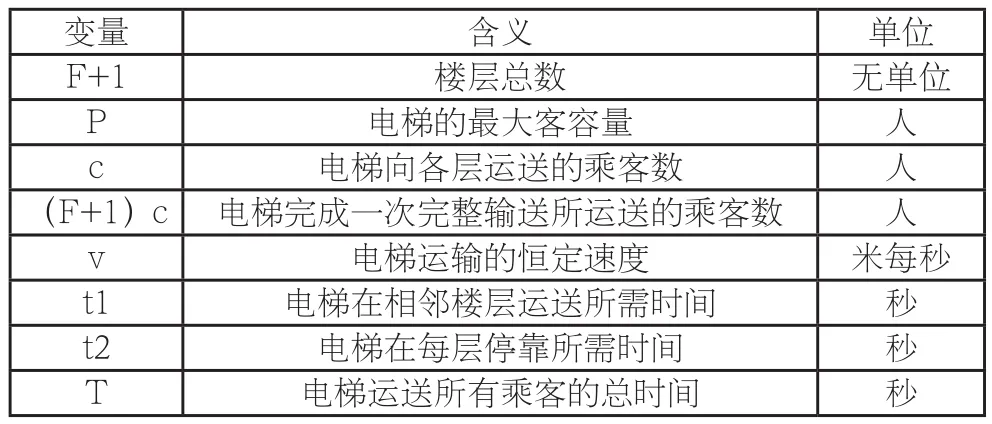
变量 含义 单位F+1 楼层总数 无单位P电梯的最大客容量 人c电梯向各层运送的乘客数 人（F+1）c 电梯完成一次完整输送所运送的乘客数 人v电梯运输的恒定速度 米每秒t1 电梯在相邻楼层运送所需时间 秒t2 电梯在每层停靠所需时间 秒T电梯运送所有乘客的总时间 秒

2 常见电梯运行模式比较

在我们生活中最常见的两种电梯运行模式则是随机和奇偶层运行，为简化描述同时不失一般性，假设有两台电梯同时运行。如果一个电梯交通系统能满足高峰期的交通需求，那么该交通系统就能满足任意时间段的运输工作。因此，这里我们考虑如何在电梯使用的高峰期，尽快的将乘客运送至目的楼层，以电梯运送所有乘客的总时间T最短，依据“电梯运行周期与运行总时间之比等于电梯在一个周期内运送的乘客与乘客总数之比”的“比例”原则，对电梯常见运行方式进行评价。

2.1 随机运行方案

此方案允许电梯上行时在任意楼层停靠，可知两台电梯理论的平均运行周期为（2Ft1+Ft2），乘客总数为2P，一个周期内实际运送的乘客数为Fc，所用时间为T.依照上述的比例原则有：

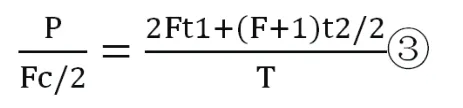
化简得：

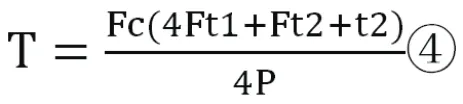
2.2 奇偶层运行方案

该方案要求两台电梯向上运行时，一台停靠奇数层，另一台停靠第一层和偶数层，现讨论F的奇偶性

（1）当F为奇数时，F+1为偶数，运行奇数层的电梯运行周期为（F-1）(2t1+t2/2),运行偶数层的电梯运行周期为【2Ft1+(F+1)t2/2】,所以电梯运送所有乘客的时间即为完成运送至偶数层的乘客所用的时间，仿照①式可得：

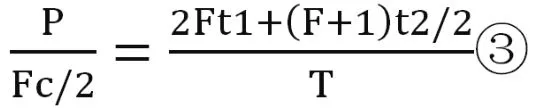
化简有：

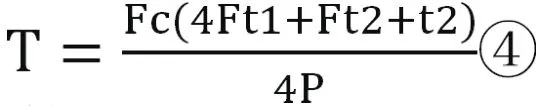
（2）当F为偶数时，F+1为奇数，运行奇数层的电梯运行周期为（2Ft1+Ft2/2）,运行偶数层的电梯运行周期为【2（F-1）t1+Ft2/2】,所以电梯运送所有乘客的时间即为完成运送至奇数层的乘客所用的时间，仿照①式可得：

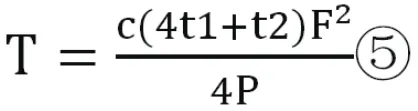
3 电梯运行模式的优化设计

研究了上述两种运行模式后，我们不妨想象一下如果将楼层分成几个板块，再分别由电梯运送，会不会使电梯的运送时间更短，现对电梯新的运行模式作假设：以（Fm+1）（0＜m＜1）层为界分为上下两段，一台电梯运行第一层至第（mF+1）层，另一台则运行第一层，第（Fm+2）层至第（F+1）层，同理可得：

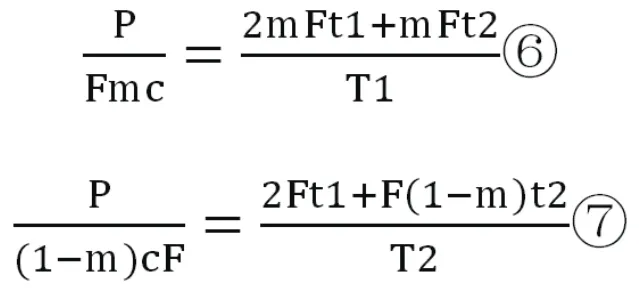
化简上述两式得：

由⑧⑨可知，当m增大时,T1增大，T2减小，所以T1是关于m的增函数，T2是关于m的减函数，令T1=T2,解得

现对m的大小进行分类讨论

当m＞n时,T1＞Tn＞T2,T=T1

当m＜n时,T1＜Tn＜T2,T=T2

当m=n时,T有最小值，此时运送所有乘客的总时间最短，即

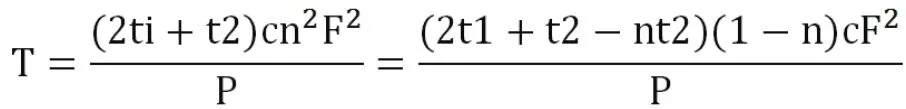
依据以上对三种模型求得的时间，观察可得分段运行模式最优。

4 电梯对临时需求的响应

电梯根据各层的用户通过面板发出的临时指令需要做出响应，各楼层发出向上或者向下的指令的概率，在一天中绝大多数的时刻服从均匀概率密度函数，在上下班等高峰段择更接近于正态分布的概率极大值点。电梯根据任意时间片段内的指令之和，综合做出对应的运行行为。楼层信息通过各层不同的赋值，可以通过计算判断对特定的指令，到底是向下运行或向上运行，在有两台以上电梯时，是否由同一台电梯并向上或向下运行至楼层的最大或最小楼层，期间出现的所有楼层信息都加入到电梯对临时需求的决策内，每到一楼层就判断临时的需求中是否有包含该楼层，有则在该层停留，并移除该层需要再停靠的信息，无则继续运行，运行至最值处，重新从临时乘梯的需求中找出最值，并判断向上或向下运行，如此循环。当一段时间内没有需求信息后，电梯选择在合适的楼层停靠等待一段时间，并实时的监测是否存在需求。

5 电梯故障响应决策

电梯运行的过程故障率是极低的，可靠性很高，但是设计者必须考虑故障时的处理方法，以避免在极小概率情况下的安全和财产损失。

考虑一个具体的情形：有4部以上的电梯，同时有3部以下的电梯发生了故障。由于电梯总体上上下人是同时进行的，这在现实中可以实现，用不同的时间起点去描述电梯的骑士运行时间，即把电梯记录故障的时刻设置不同步就可以了，也就是电梯系统运行中可能最多会有3个不同的故障，这时我们的办法是，对故障发生的楼层进行重要性的大小排序，一次只去解决一个故障，注意在响应这个故障后，电梯已经运行到了新的位置。解决完这个故障后，将这个故障在需要处理得故障清单中清除，然后再对余下剩下的电梯故障重新排序，然后继续以上的过程，直到所有的故障得以消除或者解决。人数变化时需要等待正在改变人数的电梯运行完才能变化，也就是说，一次只能一个电梯改变其内的人数，其后的电梯运行到任务楼层后只能停在原地等待，改变完的电梯会继续运动。

比如电梯楼层是0-21层，当键盘监测到22以上的输入时，则不做出任何响应，在0-21层中，只需对监听到的值进行特定的数学运算就可决定接下去如何运行。

只有一个电梯时发生故障时无法解决电梯的调度的，因此2部以上的电梯不仅是运力的需要，也是故障容错机制的必要。理论上2部电梯就会很好的运行，并且在电梯变多后，不仅带来运力的线性提升，还带来运行控制方法成倍的复杂化。因为一些并发问题使策略容易出现较为复杂的情形，这时总的原则同以上所述。

6 电梯停靠策略

并非所有的时刻电梯在都在同时被需求，实际的情况很有可能是这样：考虑电梯楼层不特别高，在相对有限的时间内能完成一次完整的运行，电梯只在一个楼层停，这样乘电梯的每个人都在这个楼层走到自己想去的楼层。那么怎么知道电梯每次在哪个楼层停下来呢？在一楼的时候每个乘客选择自己的目的层，电梯可以快速的自动计算出应停的楼层。这个应停的楼层应该保证这次乘坐电梯的所有乘客的爬楼梯层数之和最少（包括上下楼）。

7 问题分析及数学建模

该问题本质上是一个数学优化问题。首先为这个问题找到一个合适的抽象模型。从问题的场景中可以看出，有两个因素会影响到最后的结果：乘客的数量及需要停的楼层。因此，我们可以从统计到达各层的乘客数目开始分析。

假设楼层总共有N层，电梯停在第x层，要去第i层的乘客数目总数为total[i],这样，所爬楼梯的总数就是∑{total[i]*| i - x|}(i =1 , 2 , …… ,N-1,N)。因此我们的任务就是找到一个整数x使得∑{total[i]*| i - x|}(i = 1 , 2 , ……N-1, N)的值最小。及求函数：

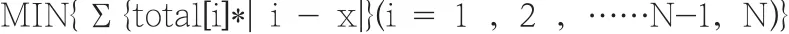
数学求解

方法一：

先考虑最简单的解决方案，然后在此基础上进行优化，可以第一层开始枚举x一直第N层，然后计算如果电梯在第x层停的话所有乘客总共要爬多少层楼。这是最为直观简洁的一个解法。

方法二：

现在我们来更仔细的分析一下这个问题，看看怎么样优化一下。假设电梯停在第i层楼，我们计算出所有乘客总共爬楼梯的层数是Q。如果有N1个乘客想去的楼层在第i层之下，有N2个乘客正好想去的楼层是第i层，有N3个乘客想去的楼层在第i层之上。这个时候，考虑一种具体的情形：如果电梯改停在i-1层，所有目的地在第i-1层以下的乘客可以少爬1层，总共少爬N1层，所有在i层及以上的乘客要多爬一层，总共多爬N2+N3层，这时总共需要爬Q-N1+N2+N3。

反之，如果电梯在i+1层停所有目的地在第i层以上的乘客可以少爬1层，总共少爬N3层，所有在i层及以下的乘客要多爬一层，总共多爬N1+N2层，这时总共需要爬Q+N1+N2-N3层。

可见，当N1＞ N2+N3 时，电梯在第i-1层楼停更好；当N1+N2＜N3 时，电梯在i+1层停更好。其他情况在第i层更好。

通过以上的讨论，电梯的运行策略需要考虑的角度较多，可以根据不同的情形建立数学方程，并且从数学的角度进行解决。

8 结束语

本文讨论了电梯运行中的规律和可能采取的运行策略。并建立了相应的数学模型，在此基础上进行了讨论和比较，给出了优化运行的方法。