气动肌肉的滑模控制仿真研究

张 猛，韩亚丽，朱松青，沈 培，吴振宇

(南京工程学院 机械学院，江苏 南京 211167)

1 引言

气动肌肉因具有较好的功率/质量比和功率/体积比，且柔顺性好，近年来成为研究的热点，并广泛用于各类服务型机器人中[1～5]。虽然气动肌肉有其优点，但由于空气的可压缩性，再加上气动肌肉力学特征本身有很强的非线性，要使气动肌肉作为柔性驱动发挥最佳效果，精确的气动肌肉建模及控制是必须的。

针对气动肌肉模型的建立，主要分为理论建模与实验数据的拟合。Schulte根据气动肌肉的几何关系、能量守恒原理以及虚功原理，将气动肌肉看做理想气缸进行建模[6]，Chou和Hannaford的研究表明气动肌肉收缩过程中库伦摩擦力占主要作用，因此忽略黏性摩擦力的作用，在Schulte模型的基础上加入库伦摩擦力以及橡胶囊厚度的影响提出了一种修正模型[7，8]。Pujanu-Arrese采用实验数据拟合的方法进行了包含气动肌肉收缩量与气动肌肉内部气压的多项式数学建模，ShameekGanguly等人考虑到摩擦力因素，建立了包含气动肌肉内部气压、肌肉收缩率和肌肉收缩变化率的多项式数学模型。

由于气动肌肉非线性特征，针对气动肌肉的控制，研究者们进行了不同控制方法的研究，Tri Vo Minh采用PI控制器进行了单根气动肌肉的控制研究[10]，V.Jouppila等[11，12]对单根气动肌肉进行了滑模控制研究和光滑可变结构滤波器相结合的控制策略，华中科技大学吴军[14]等采用基于模糊补偿的滑模控制方法进行气动肌肉研究，浙江大学的李超等[15]进行了基于微分器的滑模控制研究。对于建模方法，本文采用拉线式位移传感器，精度高，成本低。使用气缸充气提供负载，操作方便，易与调控。控制方法采用等效滑模控制，具有控制鲁棒性强，跟踪效果好等优点。

本文研究的气动肌肉拟用于下肢膝关节外骨骼机构中，在进行应用之前，需对气动肌肉的性能特性进行研究。由于气动肌肉的内部的设计和结构参数很难获取，采用理论模型很难实现气动肌肉的建模，本文采用实验拟合建模的方法对气动肌肉进行建模，并借鉴国内外研究，采用滑模控制对气动肌肉进行控制研究。

2 气动肌肉建模实验研究

搭建了气动肌肉特性分析平台，通过实验的方法得到了气动肌肉的拉力、收缩量和内部气压之间的关系。图1为原理图。图2为实物图。

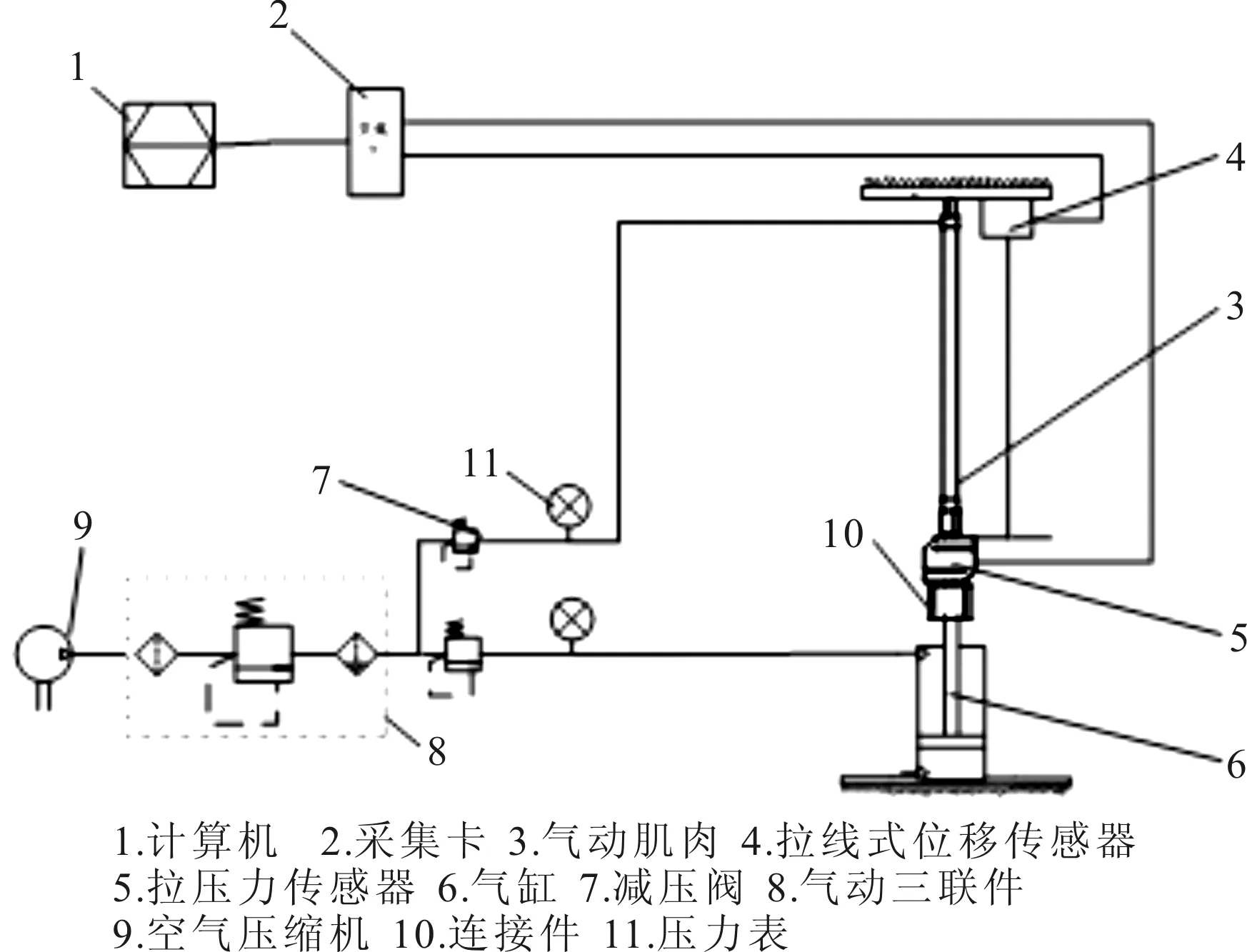
图1 气动肌肉特性分析系统原理

图2 气动肌肉特性分析实验平台

(1)等压实验。即保持气动肌肉内部气压不变，改变负载大小得到气动肌肉的收缩力(收缩拉力)与收缩量(气动肌肉原长度与收缩后长度之差)之间的关系。实验过程描述为：气动肌肉与气源之间连接有减压阀，通过减压阀调节气动肌肉的内部气压，使气动肌肉内部气压保持在0 bar,此时以同样的方式调节气缸内的气压以达到改变负载的目的，使气缸内的气压从0 bar以0.5 bar的增幅增加到5 bar，并通过气动肌肉的一端连接有拉力传感器检测到每档气压下气动肌肉所产生的收缩力以及拉线式位移传感器检测到气动肌肉的收缩量，并记录下来。完成以上实验之后调节气动肌肉内部气压保持在1 bar，再次调节负载大小同时记录对应气动肌肉的拉力和收缩量。依次类推，在气动肌肉内部气压2 bar、3 bar、4 bar、5 bar、6 bar时分别做以上实验。表1为等压实验数据。图3为等压实验折线图。可以看出在气动肌肉的气压不变时，收缩率越小，气动肌肉的收缩力越大。

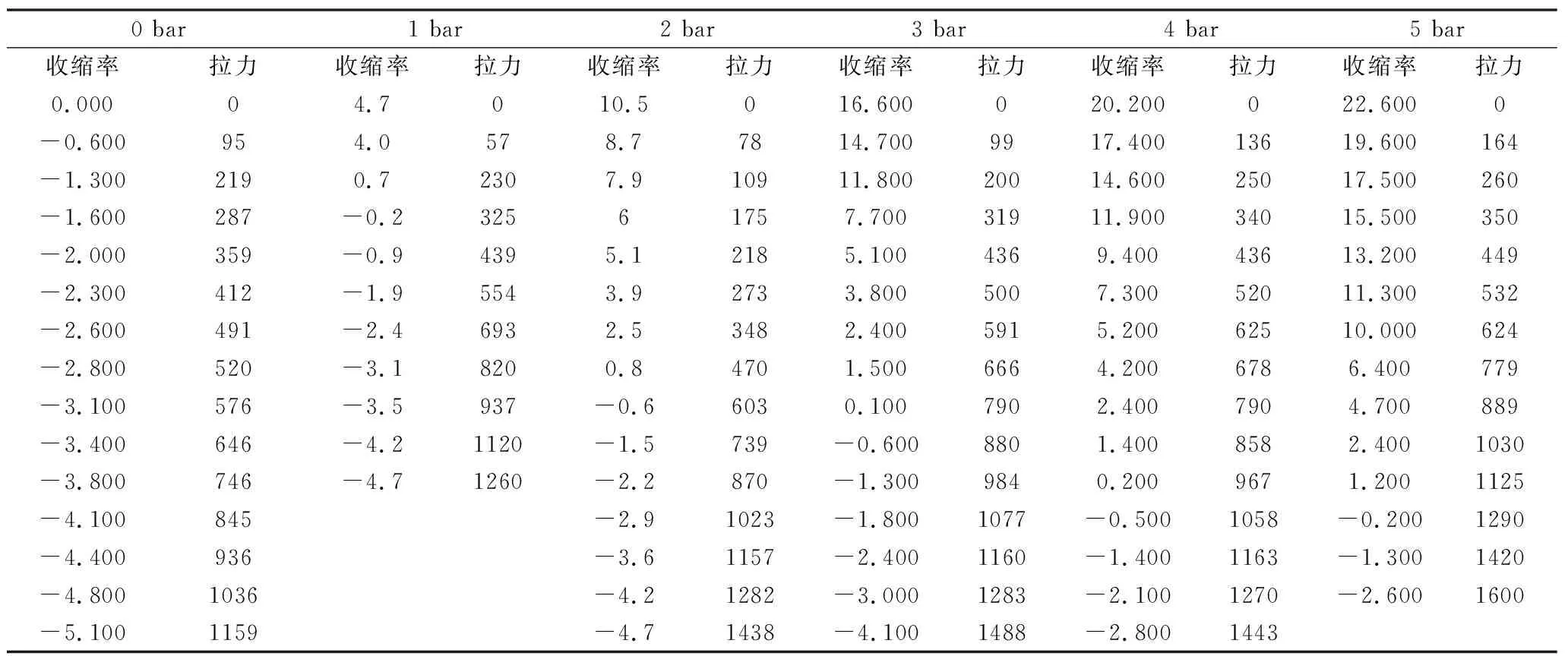
表1 等压实验数据

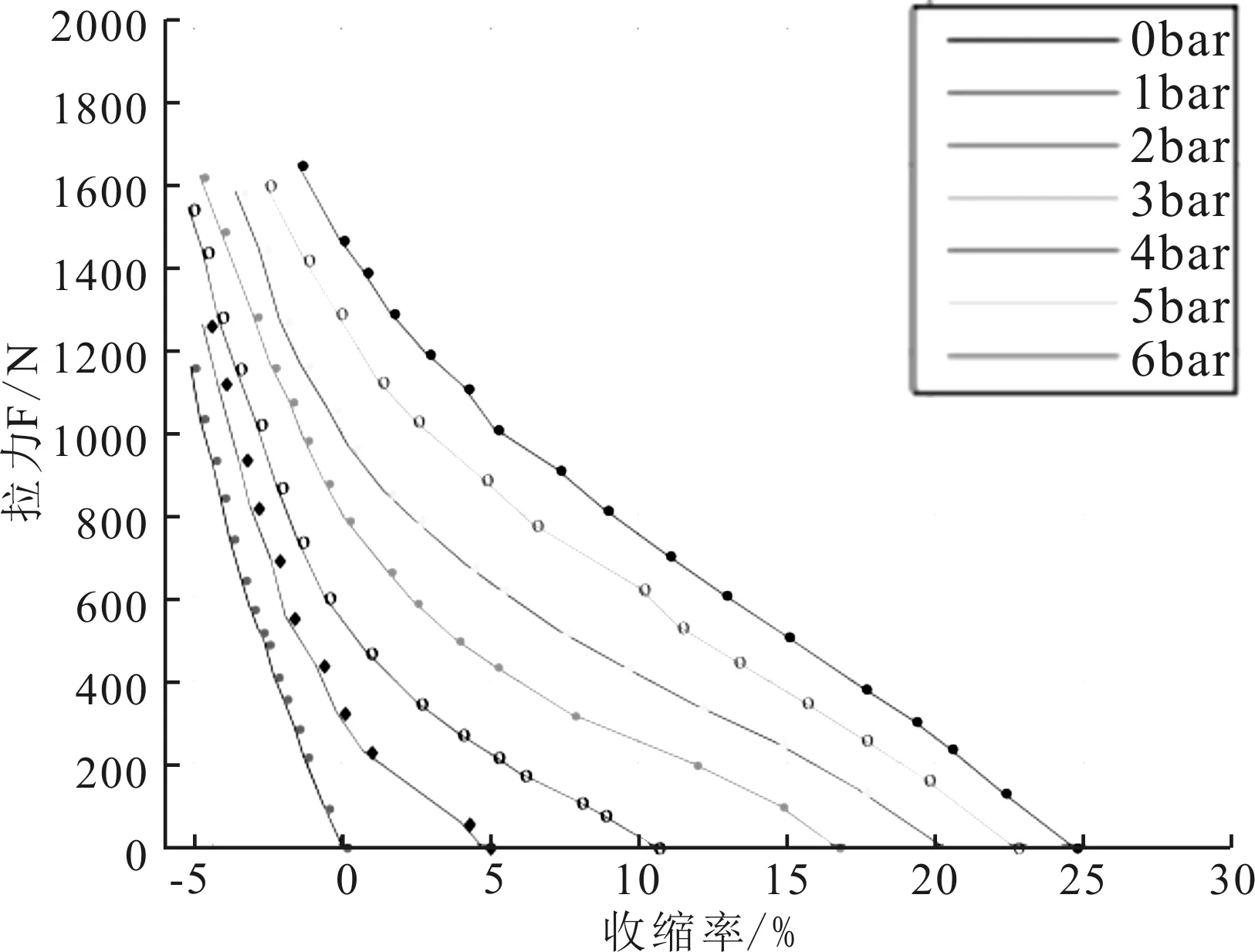
图3 气压固定时拉力与收缩率关系图

(2)等长实验。即保持气动肌肉的收缩量不变，调节气动肌肉内部气压的大小，检测气动肌肉产生的拉力。实验过程描述为：通过调节气缸内部气压的大小，使气动肌肉的收缩量保持在0 mm,然后调节气动肌肉的内部气压从1 bar开始以0.5 bar的增幅到6 bar，记录下每档气压下气动肌肉的收缩力大小。完成以上实验后调节气缸内部气压使气动肌肉的收缩量保持在10 mm，再次调节气动肌肉内部气压，记录下对应的收缩拉力。依次类推，当气动肌肉的收缩量为20 mm、30 mm、40 mm、50 mm、60 mm、70 mm、80 mm时分别做以上实验。表2为等长实验数据，图4为等长实验折线图。可以看出，当气动肌肉的收缩率不变时，其内部气压越大，收缩力越大。

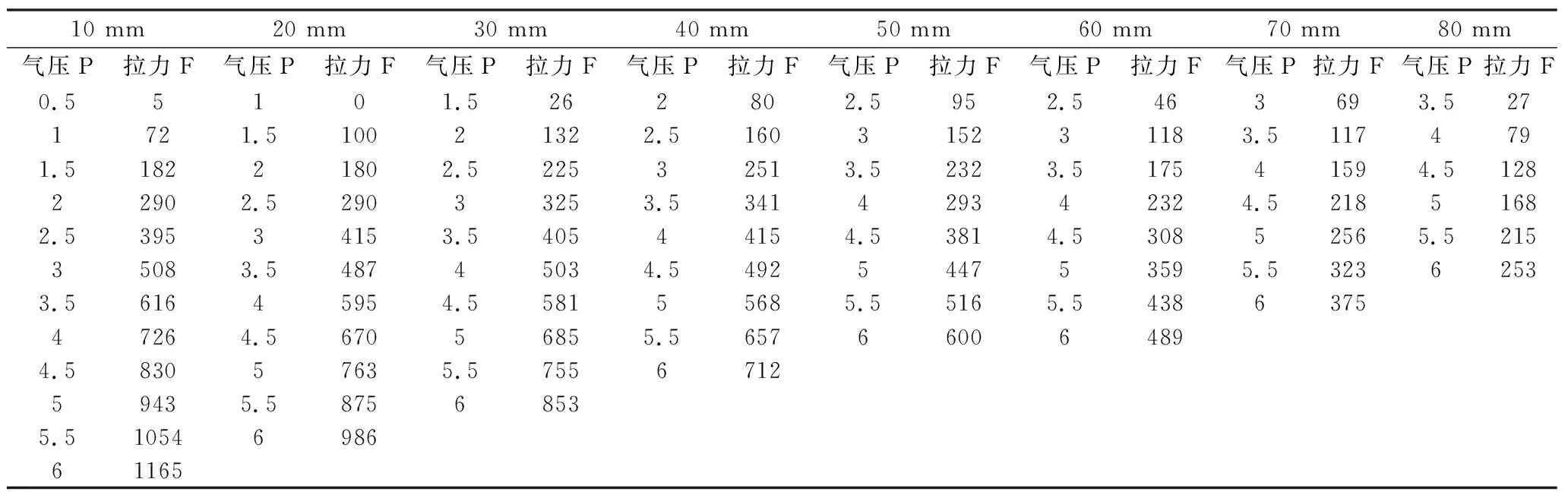
表2 等长实验数据

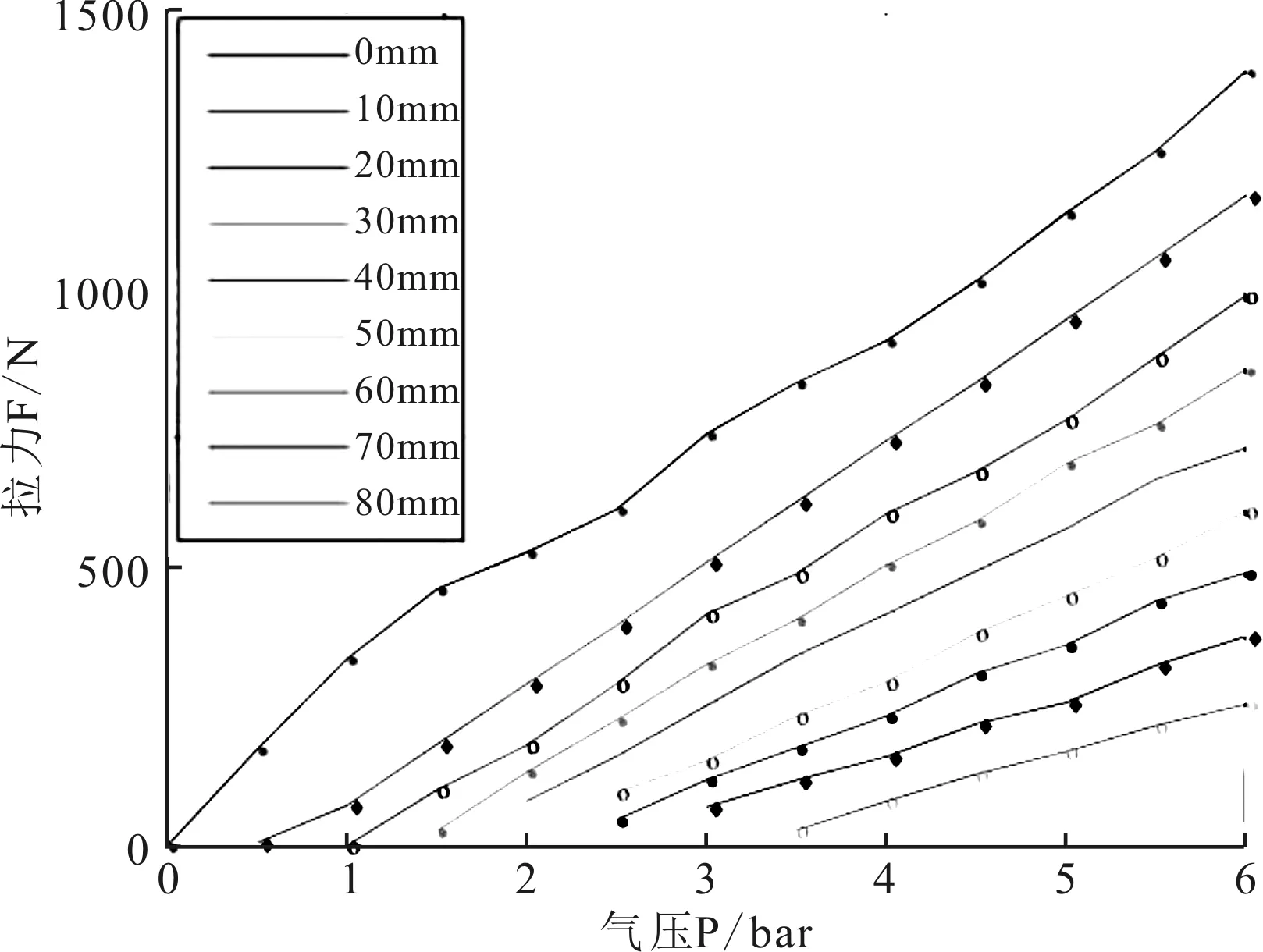
图4 收缩量固定时拉力与气压关系

(3)等张实验。即保持气动肌肉的轴向拉力不变，调节气动肌肉内部气压大小，检测对应气动肌肉的收缩量。实验过程描述为：调节连接气缸的减压阀，使气动肌肉的轴向拉力保持在200 N,然后调节气动肌肉的内部气压，使其从0 bar开始以0.5 bar的增幅增加到6 bar，记录下每档气压下对应气动肌肉的收缩量。依次类推，在气动肌肉的收缩力分别为300 N、400 N、550 N、700 N、900 N、1200 N时做以上实验，记录下对应气动肌肉内部气压与其收缩量。表3为等张实验数据，图5为等张实验折线图。可以看出，气动肌肉负载不变时，气压越大，收缩拉力就越大。并且成线性关系。

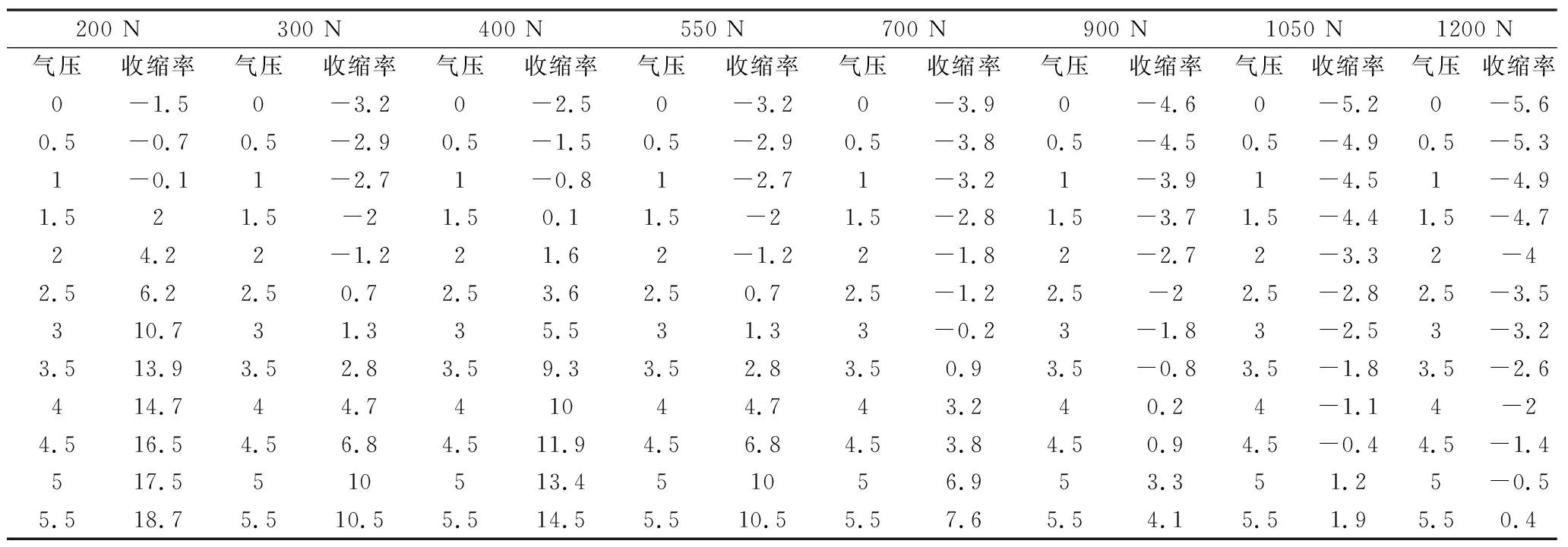
表3 等张实验数据

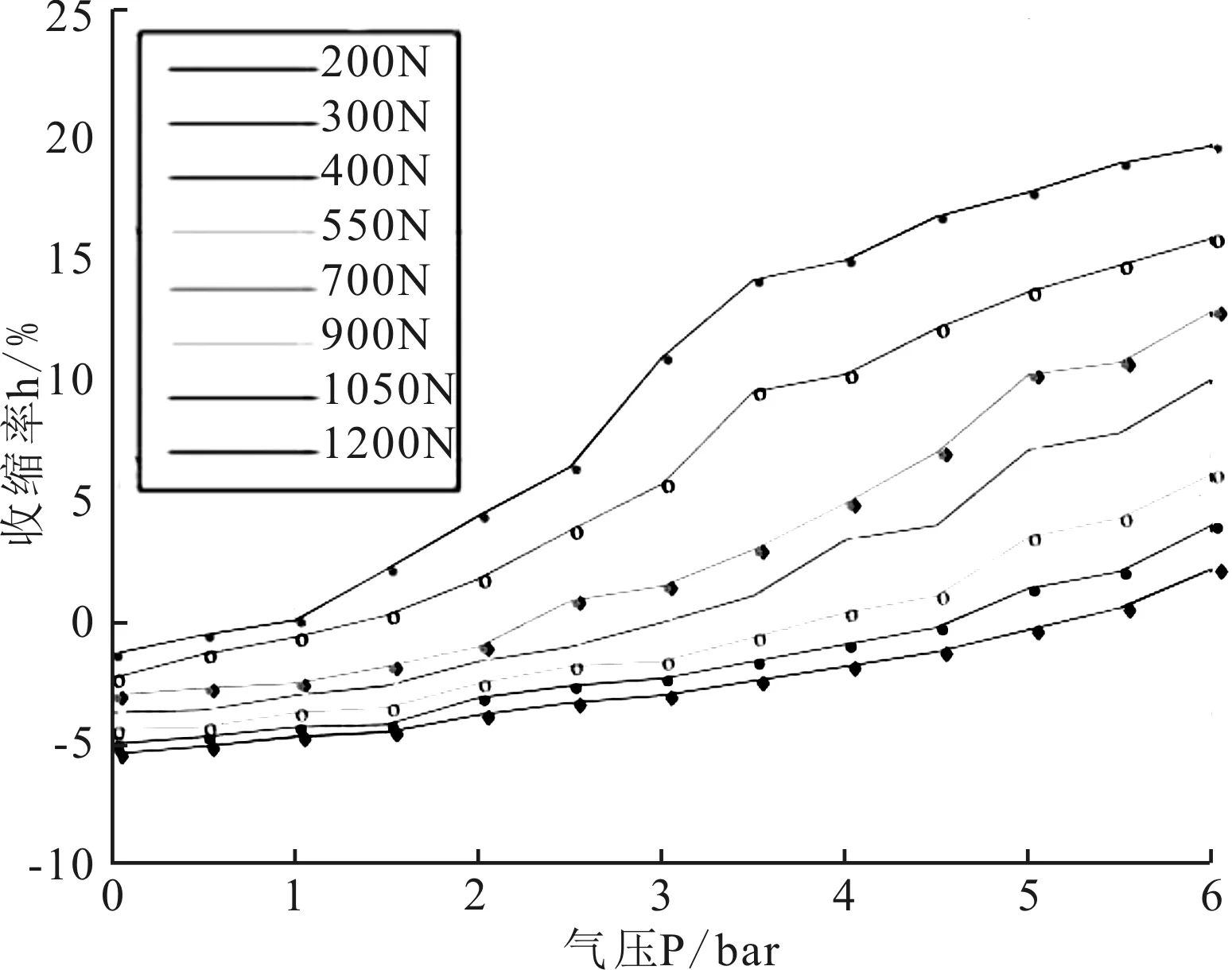
图5 收缩力固定时收缩率与气压关系

通过三项实验可以得到较为全面的气动肌肉3个参数之间的关系，以使建模更加精确。从图3～5可以直观地看出在气动肌肉的3个参数中保持其中一个不变时，另外两个参数之间的变化趋势关系，特别的，在等长实验中可以看出在收缩量不变时，气动肌肉的气压和收缩力成线性关系。同时，基于Pujanu-Arrese提出的多项式模型[9]，利用Matlab中lsqcurvefit(最小二乘法)函数对所有实验数据进行拟合，得到气动肌肉拟合模型如式(1)所示：

F(P,ε)=(43.1759+225.6671P)+(-103.2922-4.7673)ε+12.9757-0.1628ε-0.7097ε3+0.0143ε4

(1)

3 单根气动肌肉的滑模控制研究及仿真

采用滑模控制[16,17]对单根肌肉进行控制研究，控制阀选用的是FESTO公司的三位五通高速比例方向阀MPYE-5-1/8-LF-010-B，用等效节流孔模型对开关阀的质量流量描述如式(2)所示：

(2)

负载一定时，气动肌肉的体积与收缩量成正比关系，通过实验数据进行以如下公式进行拟合，如式(3)所示：

V(x)=V0+V1x

(3)

式(3)中，V0和V1为拟合曲线系数，V(x)为气动肌肉的体积，x是气动肌肉的收缩量。

气动肌肉内部的压力微分方程如式(4)所示：

(4)

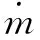
当气动肌肉负载固定时，对气动肌肉充放气进行控制，动力学模型如式(5)所示:

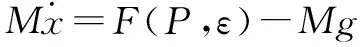
(5)

式(5)中，M为等效惯性质量，x为气动肌肉的收缩量，F(P,ε)为气动肌肉的输出力，g为重力加速度。

对式(5)进行微分，得到系统模型如式(6)所示：

(6)

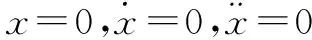
(7)

(8)

当M=10 kg时，将l0=0.424m,a1～a8带入(7)和(8)可得式(9)：

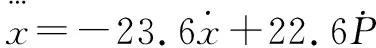
(9)

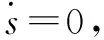
等效控制的作用在于保证气动肌肉的收缩状态在滑模面上，切换控制的作用在于保证气动肌肉的收缩状态不离开滑模面。对于三阶系统，定义以下二阶滑模面，如式(10)所示：

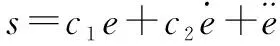
(10)

其中，e为轨迹跟踪误差(e=xd-x)。

令c1=23.6,c2=0

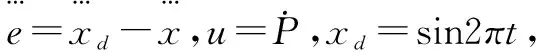
(11)

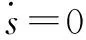
(12)

设计切换控制律如式(13)所示：

(13)

其中，b=22.6,K>0，设K=0.1

滑模控制律由等效控制项和切换控制项组成，即

u=ueq+use

(14)

将式(14)代入式(11)得式(15):

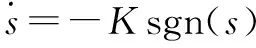
(15)

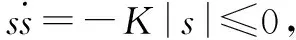
(16)

控制律中usw为鲁棒项，用于克服干扰。

基于前文理论分析，采用Matlab/Simulink进行滑模控制仿真研究，调节滑模参数得到以下仿真结果，控制输入u如图6，仿真输出结果如图7所示，图7中的(a)、(b)、(c)分别为位置跟踪、速度跟踪与加速度跟踪图。

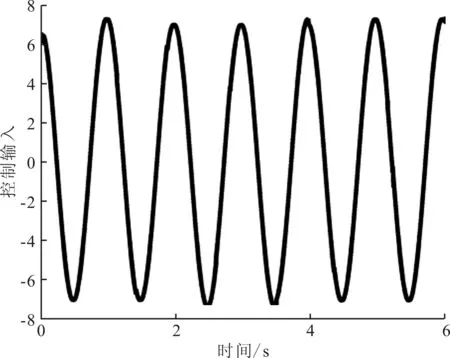
图6 仿真输入

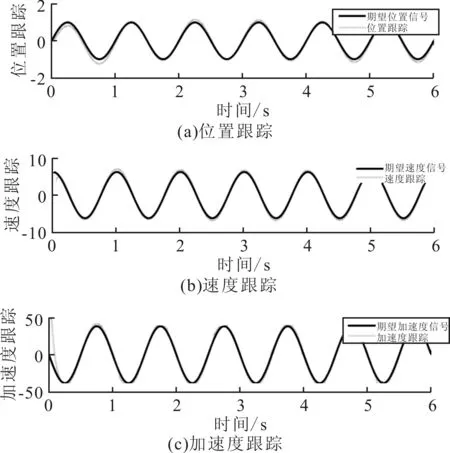
图7 仿真输出

由仿真结果可知，滑模控制在位置、速度和加速度控制上都具有很好的跟踪效果并且都具有很好的稳定性。控制非线性较强的气动肌肉，滑模控制依旧可以很好地满足对气动肌肉的控制要求。

4 结语

实验运用最小二乘拟合的方法对气动肌肉进行建模，得到了气动肌肉的参数模型。通过理论分析得到滑模控制律，并采用Matlab/simulink进行仿真分析，仿真结果表明滑模控制对系统的位置、速度、加速度具有较好的跟踪效果，后续的研究包括滑模控制算法与其它控制算法的比较，以及对气动肌肉实施控制的实验研究。