一类李超代数的中心扩张
谷翠梅,王 艳
(天津大学数学学院,天津 300354)
文献[1]给出了Balinsky-Novikov超代数(简称为BN超代数)的定义,其通过仿射化构造可得到无限维李超代数.本文中的李超代数就是由一类2|2维BN超代数仿射构造得到的,它们的偶部都是中心为0的W(2,2)李代数.通过对应2|2维BN超代数上满足一定条件的双线性型,构造得到了这些李超代数的2维上闭链,并验证所得的这些2维上闭链都是线性无关的,且正好是对应超代数2维上同调群的一组基.文中的数域都是复数域C.
1 预备知识






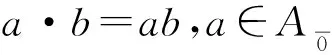



且具有以下运算关系:
[a[m],b[n]]=((m+1)ab-(n+1)ba)[m+n],
[u[r],v[s]]=(u∘v)[r+s].


e1e1=e1,e1e2=e2,e2e1=e2,
(1)


表1 李超代数Wi(i=1,…,7)的运算
2 主要结果
设g是域C上的李超代数. 若线性函数φ:g⊗g→C满足:
φ(x,y)=-(-1)|x||y|φ(y,x),
φ(x,[y,z])=φ([x,y],z)+(-1)|x||y|φ(y,[x,z]),∀x,y,z∈g.
则称φ为g上的一个2维上闭链,记Z2(g,C)为g上所有2维上闭链的集合.若存在一个线性函数f:g→C使得
φ(x,y)=f([x,y]),∀x,y∈g,
则称φ为g上的一个2维上边界,记B2(g,C)为g上所有2维上边界的集合.商空间H2(g,C)=Z2(g,C)/B2(g,C)称为g的2维上同调群.由文献[3]可知要研究李超代数g经由C的一维中心扩张,只需计算H2(g,C).

(1) (反)对称性
fi(a,b)=(-1)i+1fi(b,a),fi(u,v)=(-1)i+1fi(v,u),fi(a,u)=fi(u,a)=0;
(2) 不变性1
f1(ac,b)=f1(a,bc),f1(ua,v)=f1(u,va),
f1(a,u∘v)=f1(au,v)+f1(u,av)+f1(ua,v);
(3) 不变性2
f2(ac,b)=f2(a,bc)=f2(ca,b)+f2(a,cb),
f2(a,u∘v)=2f2(au,v)=-2f2(u,av),f2(ua,v)=f2(u,va);
(4) 不变性3
f3(ac,b)=f3(a,bc)=f3(ca,b),
2f3(a,u∘v)=2f3(au,v)=2f3(u,av)=f3(ua,v)=f3(u,va).
令

设Lε(A)(ε=0或1)是由A通过Balinsky’s构造得到的李超代数,则可定义Lε(A)上的双线性型αi:Lε(A)⊗Lε(A)→Lε(A)(i=1,2,3),
αi(a[m],b[n])=fi(a,b)βi(m,n),
αi(a[m],u[r])=0,
αi(u[r],v[s])=fi(u,v)γi(r,s).
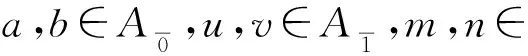
引理2.1[4]如上定义的αi是Lε(A)(ε=0或1)的2维上闭链,当且仅当fi满足相应的(反)对称性和不变性i(i=1,2,3).
文献[4]给出了引理2.1当ε=1时的证明,可类似得到ε=0的情形.
利用引理2.1,下面将通过Wi(i=1,…,7)对应BN超代数上的不变双线性型来确定Wi上的2维上闭链.


(2)
(3)

(4)
(5)



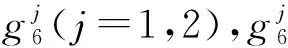






设α:W1×W1→C是W1的一个2维上闭链;f:W1→C是W1的一个线性函数,其作用定义如下:

此外,定义αf=α+φf,其中φf∈B2(W1,C).
首先计算ε=0时,αf的非零作用(∀m,n,r,s∈Z).
根据αf(L0,[Lm,Ln])=αf([L0,Lm],Ln)+αf(Lm,[L0,Ln]),可得
(m-n)αf(L0,Lm+n)=-(m+n)αf(Lm,Ln).
而由αf(L0,Ln)=α(L0,Ln)+f([L0,Ln])=0,易知αf(Lm,Ln)=0(m+n≠0). 设a(n)=αf(Ln,L-n),由αf(Lm+n,[L-m,L-n])=αf([Lm+n,L-m],L-n)+αf(L-m,[Lm+n,L-n]),可得
(m-n)a(m+n)=(m+2n)a(m)-(2m+n)a(n).
(6)
在(6)式中令n=1,则
(m-1)a(m+1)=(m+2)a(m)-(2m+1)a(1).

(7)
根据αf(L0,[Lm,In])=αf([L0,Lm],In)+αf(Lm,[L0,In])可得
(m-n)αf(L0,Im+n)=-(m+n)αf(Lm,In).
而由αf(L0,In)=α(L0,In)+f([L0,In])=0,易知αf(Lm,In)=0(m+n≠0). 设b(n)=αf(Ln,L-n),由
αf([Lm,Ln],I-m-n)=αf(Ln,[I-m-n,Lm])-αf(Lm,[I-m-n,Ln]),
可得
(m-n)b(m+n)=(m+2n)b(m)-(2m+n)b(n).
(8)
在(8)式中令n=1,则
(m-1)b(m+1)=(m+2)b(m)-(2m+1)b(1).

(9)
据αf(L0,[Gr,Gs])=αf([L0,Gr],Gs)+αf(Gr,[L0,Gs])可得αf(L0,Ir+s)=-(r+s)αf(Gr,Gs).而αf(L0,In)=α(L0,In)+f([L0,In])=0,易知αf(Gr,Gs)=0(r+s≠0).设p(r)=αf(Gr,G-r),显然p(r)=p(-r),根据αf(Lr+s,[G-r,G-s])=αf([Lr+s,G-r],G-s)+αf(G-r,[Lr+s,G-s]),可得
2b(r+s)=(3r+s)p(s)+(r+3s)p(r).
(10)
在(10)式中令s=1,则
2b(r+1)=(3r+1)p(1)+(r+3)p(r).
又由于







