直线共轭内啮合齿轮副的重合度研究

段 刚， 崔建昆， 高铭良

（上海理工大学 机械工程学院，上海 200093）

直线共轭内啮合齿轮副的核心是一对特殊齿形的齿轮副，构成齿轮副的外齿轮齿廓为左右对称的直线，内齿圈齿廓为与外齿轮齿廓共轭的曲线，外齿轮和内齿圈均为圆柱齿轮。

与外啮合齿轮副相比，这种内啮合齿轮副中心距小，而且两齿轮回转方向相同，相对角速度较小，所以，构成了该传动方式最突出的优点：滑动系数小、噪声低[1]。

目前直线共轭内啮合齿轮副运用最广泛的是在内啮合齿轮泵中。率先成功研发第一台直线共轭内啮合齿轮泵的是瑞士Turninger公司[2]，其齿数比为13：17，结构简单，输出的工作压力很容易达到20 MPa，其噪声最小可达53 dB，在行业内被称为安静泵。

上海航空发动机制造厂设计制造了NB系列直线共轭内啮合齿轮泵，NB泵既具有一般齿轮泵结构简单、对介质污染敏感性小的优点，又具有柱塞泵的高压力和螺杆泵的低噪音、长寿命的优点，是目前国内最先进、最具有竞争力的定量泵。

本文根据齿轮啮合原理，推导出直线共轭齿轮副的啮合曲线，推导出直线共轭内啮合齿轮传动重合度的计算公式，针对关键的齿形参数对重合度的影响进行实例研究。

1 外齿轮基本参数

在直线共轭内啮合齿轮副中，外齿轮齿廓为图1所示的左右对称的直线，其中，θ为分度圆上齿厚所对应的圆心角，β为外齿轮的齿形半角，r1为外齿轮分度圆半径，L为外齿轮中心到轮齿一侧直线的距离。直线齿廓外齿轮上的压力角在齿廓各点不一样，仿照渐开线齿轮的参数设置，规定齿轮齿廓曲线分度圆上的压力角为标准压力角，用α表示。

以外齿轮中心o1为原点建立坐标系（o1-x，y），则可得

式中，z1为外齿轮齿数。

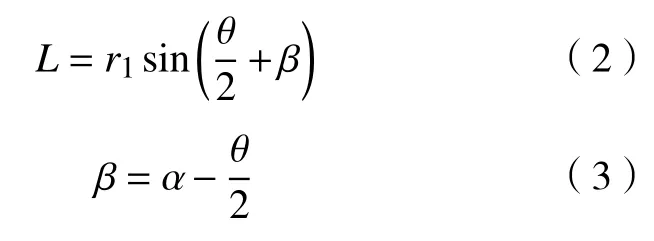
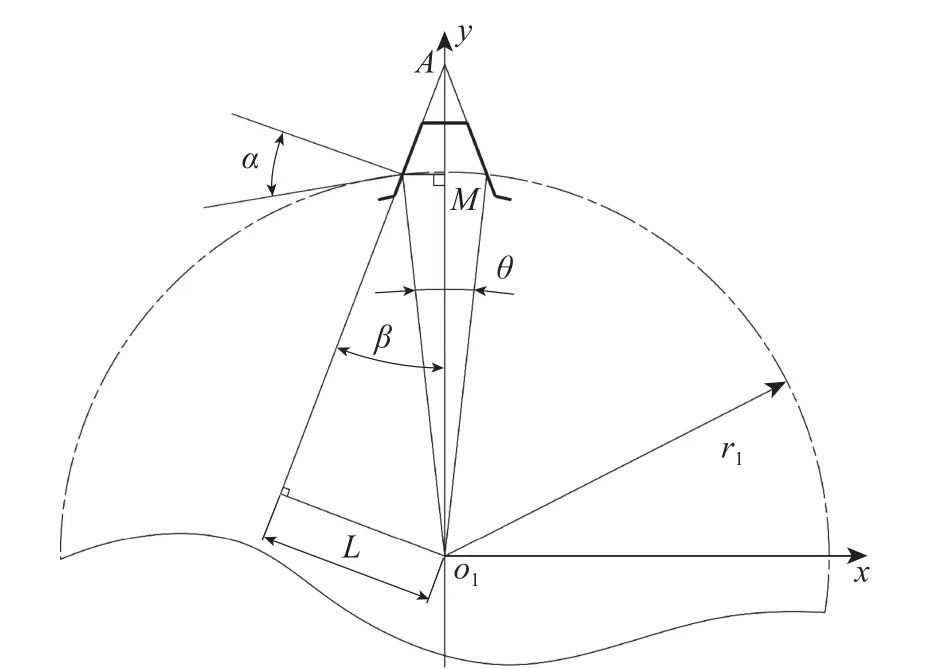
图 1 直线共轭内啮合齿轮副外齿轮齿廓Fig. 1 External gear tooth profile of the internal meshing gear pair with a straight line tooth profile out gear

由此可见，当压力角一定时，齿数越小，齿形半角越小。同时，曲线与x轴的交点表示设定参数条件下的最小齿数，如图2所示。

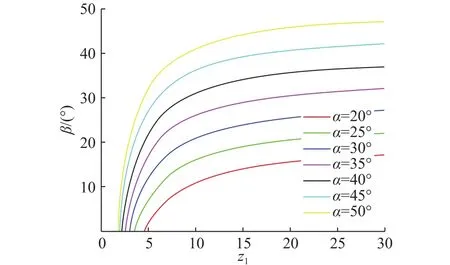
图 2 β与z1的关系Fig.2 Relationship between β and z1

由图1可以得出齿轮左侧齿廓直线方程为

2 齿高限制

在直线共轭齿廓中，外齿轮的齿廓左右对称，因此，其齿顶最高不会超过齿廓与对称轴的交点A，如图3所示。但事实上，点A不一定就是内外齿轮齿廓啮合时的极限点， 经过齿轮齿廓上的一点M作齿轮齿廓的法线，交节圆于P1点；将M点连法线沿齿廓向上平移，则P1点也在节圆上向右移动，最终到切点Pc，此时的啮合点C才是齿轮齿廓的啮合极限点。超过啮合极限点的齿廓CA因没有共轭曲线，而且齿高过高，可能在齿轮啮合过程中会发生齿廓干涉现象。啮合极限点C也可能在A点的上方，由于轮齿采用对称齿形，C点超过A点的线段并没有实际意义，因此，在设计过程中，可以规定齿顶不能超过C点和A点中y轴坐标较小的点。

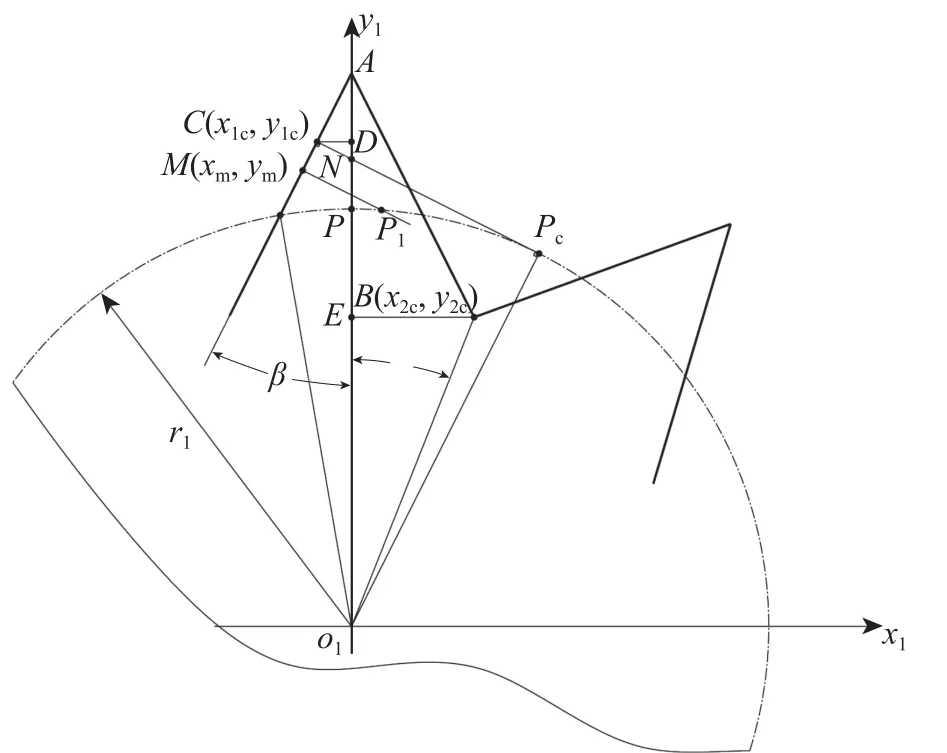
图 3 啮合极限点Fig.3 Meshing limit points

当外齿轮的齿数和压力角确定时，外齿轮的齿形也就随之确定，因此，齿轮齿槽两侧的直线齿廓在齿根相交于B点，称为齿根极限点。

3 啮合线方程

啮合线是齿轮副啮合过程中，啮合点在固定坐标系中的轨迹，可以通过齿廓法线法来进行求解。啮合线可以表达齿轮副的啮合特性，还可以用于直线共轭齿廓重合度的分析。

图4为两齿轮的啮合原理图，当齿廓上任一点K为啮合点时，外齿轮需逆时针旋转ψ1，此时，R1和R2分别为K点到外齿轮和内齿圈中心的距离，a为中心距。根据勾股定理，可得

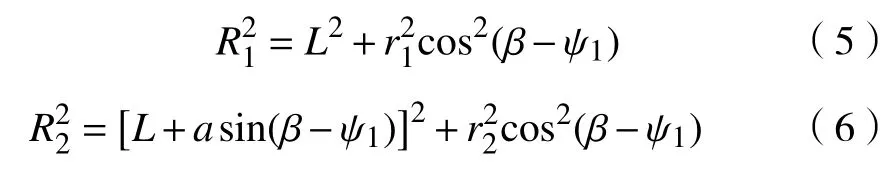
设两轮的传动比为i12，外齿轮的分度圆半径为r1，其齿廓曲线为g1，内齿圈的分度圆半径为r2。在图4中，以内外两齿轮节圆切点P为原点建立固定坐标系（P-x，y）；以o1为原点建立坐标系（o1-x1，y1），它与外齿轮固联并随它一起旋转；以o2为原点建立坐标系（o2-x2，y2），它与内齿圈固联并随它一起旋转。

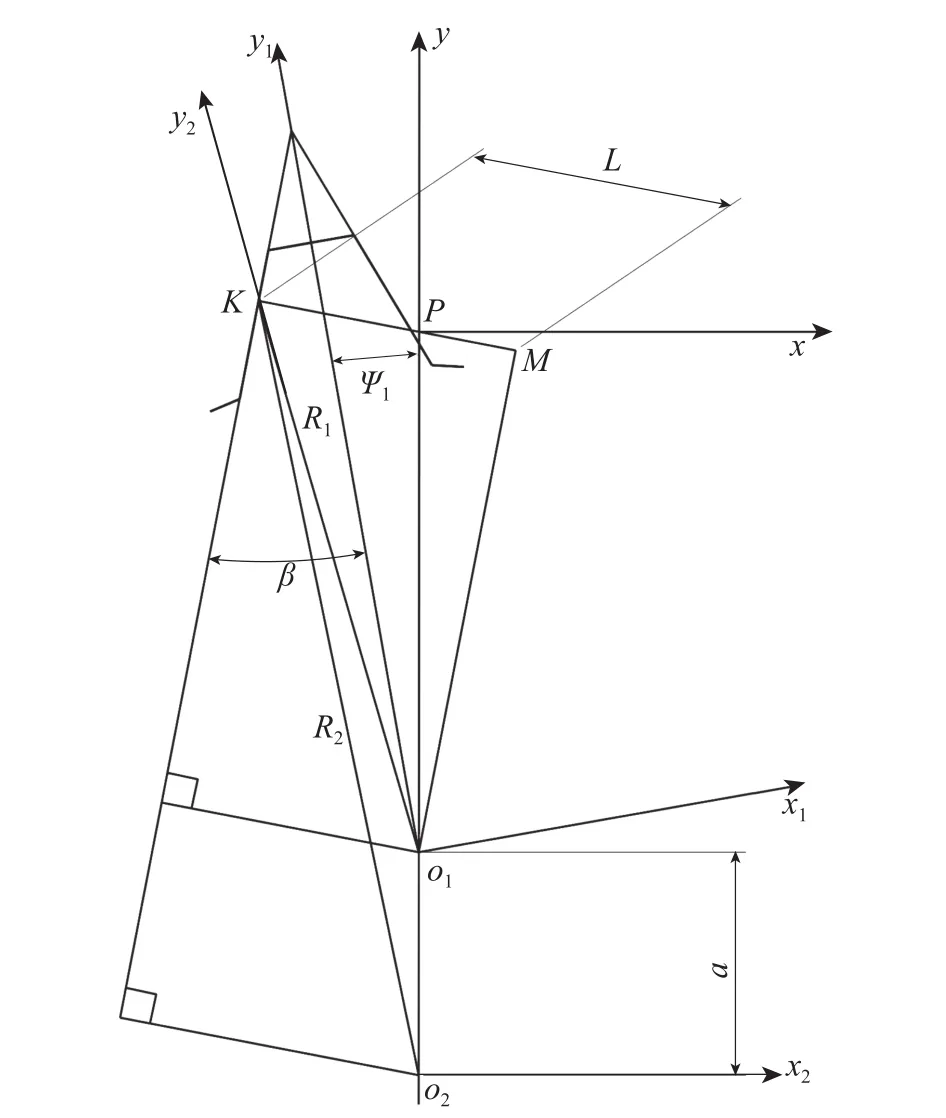
图 4 啮合局部几何关系Fig. 4 Local geometric relationships in engagement

初始位置如图5所示，两齿轮齿廓在K点接触，K1为齿廓g1上的任意一点，它在坐标系（o1-x1，y1）中的坐标为（x1，y1），外齿轮齿廓g1在K1点处的法线为K1P1，且与外齿轮节圆相交于点P1。

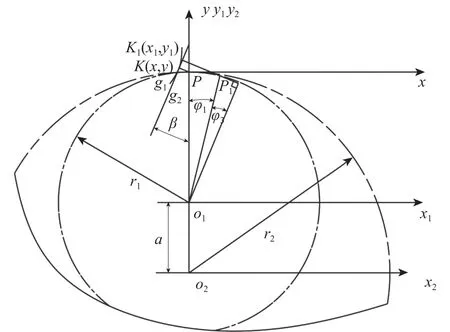
图 5 齿轮副在K点啮合Fig.5 Gear pairs conjugating at point K

如果要使K1点成为接触点，则必须将外齿轮连同其坐标系（o1-x1，y1）相对于其初始位置逆时针旋转角度φ1；与此同时，内齿圈也将连同其坐标系（o2-x2，y2）按传动比i12相对于其初始位置逆时针旋转角度φ2，如图6所示（见下页）。此时K1点在固定坐标系（P-x，y）的坐标（x，y）即为两齿轮的啮合线对应点的坐标。根据坐标变换原理[3]可得啮合线方程为

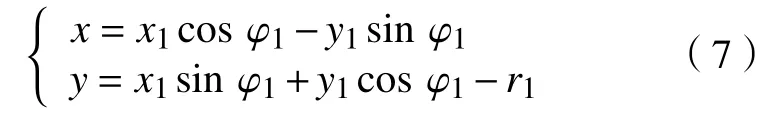
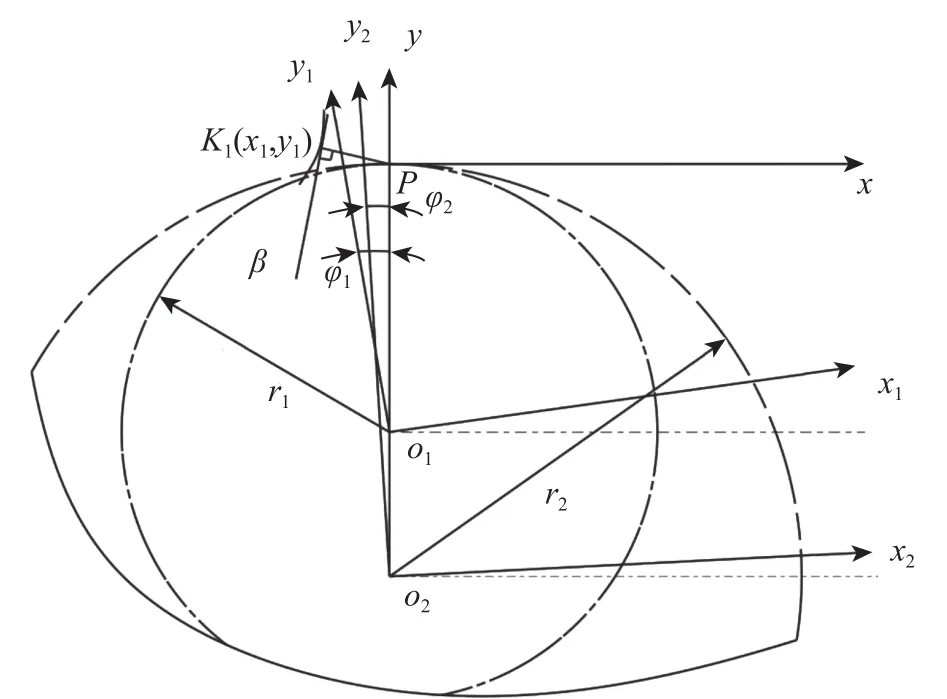
图 6 齿轮副在K1点啮合Fig.6 Gear pairs conjugating at point K1

取齿轮副为例，参数如下：z1=13，z2=20，r1=23.493 mm，β=22.5°，a=12.65 mm，外齿轮齿顶圆半径ra1=25.62 mm，内齿圈齿顶圆半径ra2=38.7 mm。

通过软件Matlab可以得到啮合线，如图7所示。由图7可以看出，相比于渐开线齿轮的直线型啮合线，直线共轭内啮合齿轮副为曲率逐渐增大的曲线，这代表着他们的啮合特性有着很大的区别。同时，由于渐开线齿轮的基圆半径不会因齿轮位置的移动而改变，所以，当渐开线齿轮副中心距有变动时啮合线不会发生变化，而直线共轭齿轮副的啮合线会因为中心距的变化而改变。

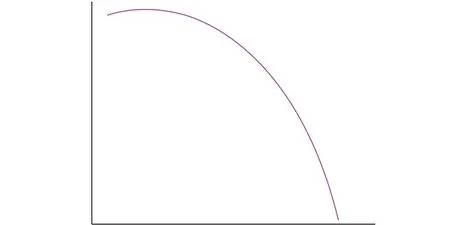
图 7 直线共轭内啮合齿轮副的啮合线Fig.7 Meshing line of the internal meshing gear pair with a straight line tooth profile out gear

4 重合度

重合度的大小表示同时参与啮合的轮齿对数的平均值。重合度大意味着同时参与啮合的轮齿对数多，提高了齿轮传动的平稳性和承载能力。但对于齿轮泵，如果重合度太大又会引起困油现象[4]。

由于直线共轭内啮合齿轮副与渐开线内啮合齿轮副的啮合线不同，在渐开线内啮合齿轮副中，该种啮合方式的重合度可以通过实际啮合线的长度与法向齿距的比值来确定。然而，由于直线共轭内啮合齿轮副与渐开线内啮合齿轮副的啮合线不同，所以，直线共轭内啮合齿轮副的重合度就不能单纯地应用渐开线齿轮副重合度的计算方法计算[5]。根据齿轮的啮合原理，可以得出一种较新的重合度ε计算方法。

式中：φ为啮合作用角；φ为周节圆心角。

周节圆心角为一个周节所对的圆心角，即

于是，还需要确定齿轮在啮合时的转角φ。在内啮合齿轮传动中，两齿轮在啮合传动时，总是从外齿轮的齿根部分和内齿圈的齿顶部分的接触点开始啮合。

当啮合点运动到外齿轮齿顶圆与内齿圈的齿根的接触点时，两齿轮齿廓将脱离接触，该接触点即为终止啮合点。

如图8所示，ra1为外齿轮齿顶圆半径，ra2为内齿圈齿顶圆半径。根据啮合原理，齿轮副从内齿圈的齿顶圆处开始啮合，从外齿轮的齿顶圆处脱开，即A点为啮合起始点，B点为啮合终止点，曲线段AB则为实际啮合线，设计量起始位置为x1轴，齿轮进入啮合时的转角为φ01，齿轮脱离啮合时的转角为φ02。当相互啮合的一对齿轮的参数确定后，就可以根据啮合线方程和两齿轮的齿顶圆和齿根圆来确定这对齿轮在啮合时的起始啮合角φ01及终止啮合角φ02，即

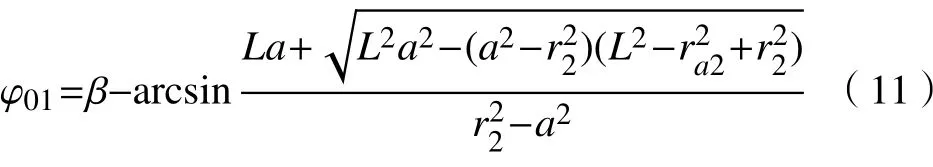
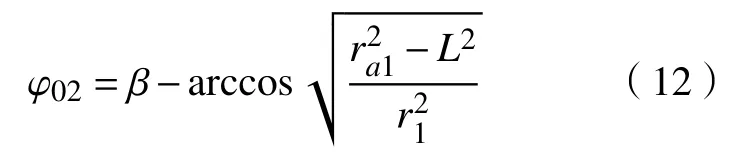
由此可得直线共轭内啮合齿轮传动的重合度ε的计算公式为

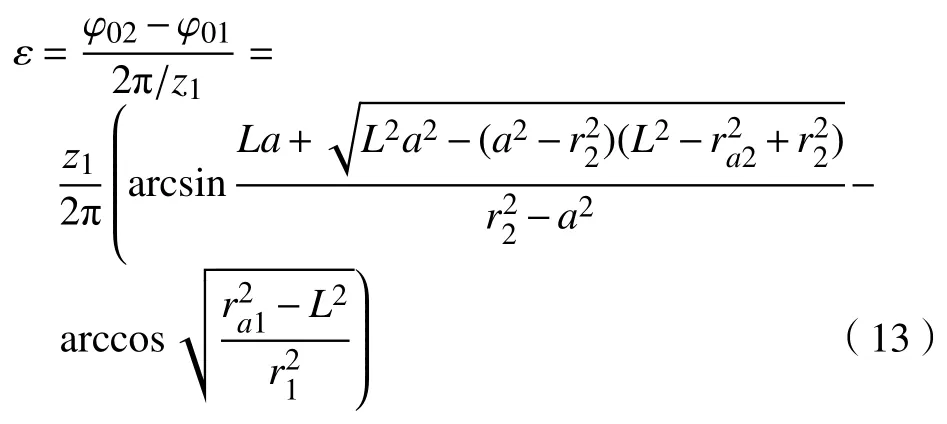
将前后的基本参数代入式（13），可得ε=1.218 6。

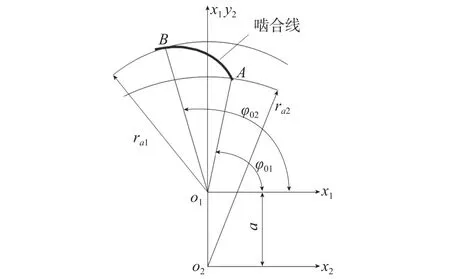
图 8 内外齿轮啮合转角Fig.8 Conjugate angle of the internal and external gears

5 重合度的影响因素分析

从重合度的计算公式中可以看出，外齿轮的齿顶圆半径ra1，内齿圈的齿顶圆半径ra2和距离L等参数同齿轮传动的重合度ε有直接关系。但是，外齿轮中心到轮齿齿廓一侧直线的距离L在设计中没有直观的几何意义，所以，研究其与重合度的关系也没有什么重要的意义。外齿轮和内齿圈齿顶圆半径受齿轮的齿顶高系数影响最大，所以，可以研究齿顶高系数来代替齿顶圆半径。同时，对于直线共轭内啮合齿轮副，如果再已知压力角α，就能确定齿轮的具体齿形。所以，压力角α对于重合度的影响也是一个重要的研究对象。

5.1 外齿轮齿顶高系数的大小对重合度ε的影响

由于重合度ε与外齿轮齿顶圆半径ra1有密切关系，在其他条件不变的情况下，通过改变外齿轮齿顶高系数的大小来观察其与重合度ε的关系。由于受到式（12）的限制，因此，外齿轮齿顶圆半径ra1有一最大极限值，即所以，对于外齿轮齿顶高系数也有极限值。

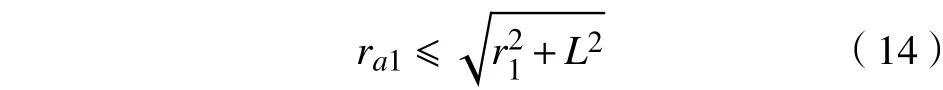
但是，如果重合度太大，就会引起困油现象[6]，所以，外齿轮的齿顶高系数就不能取太大的值。

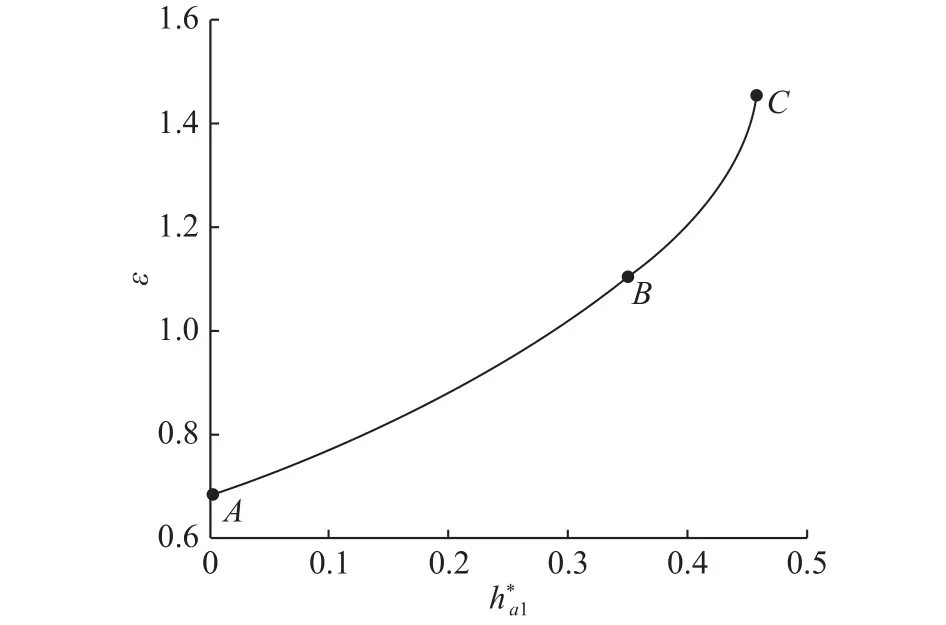
图 9 与ε的关系Fig.9 Relationship between and ε

此外，由于齿高h与外齿轮齿顶圆半径为非独立关系，从而可以得到h与外齿轮转角φ的关系图应与图9类似，事实验证也确实如此，如图10所示（见下页）。

由式（13）还可以看出，重合度ε与内齿圈齿顶圆半径ra2有关联，影响齿顶圆半径最重要的因素为齿顶高系数。内齿圈齿顶圆半径ra2的取值又受到式（11）的限制，因此，内齿圈齿顶高系数也有一定的取值范围。显然，内齿圈齿顶圆半径ra2应小于或等于内齿圈分度圆半径r2，即

5.2 内齿圈齿顶高系数的大小对重合度ε的影响

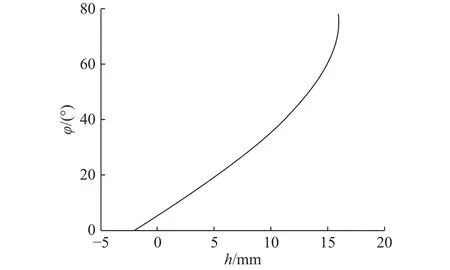
图 10 外齿轮齿高与其啮合转角的关系Fig.10 Relation between the tooth height of the external gearand its meshing angle

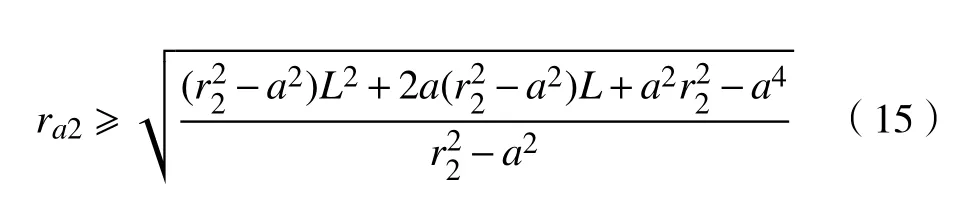
根据直线共轭内啮合齿轮泵的实际运动情况，内齿圈齿顶圆半径ra2又要受到外齿轮的齿根圆半径rf1的限制，如图11所示，为了方便计算，图中将内齿圈齿顶圆半径ra2近似表示，即得

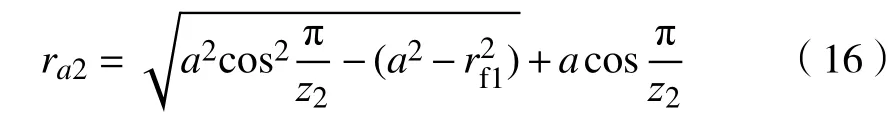
式中，z2为内齿圈齿数。

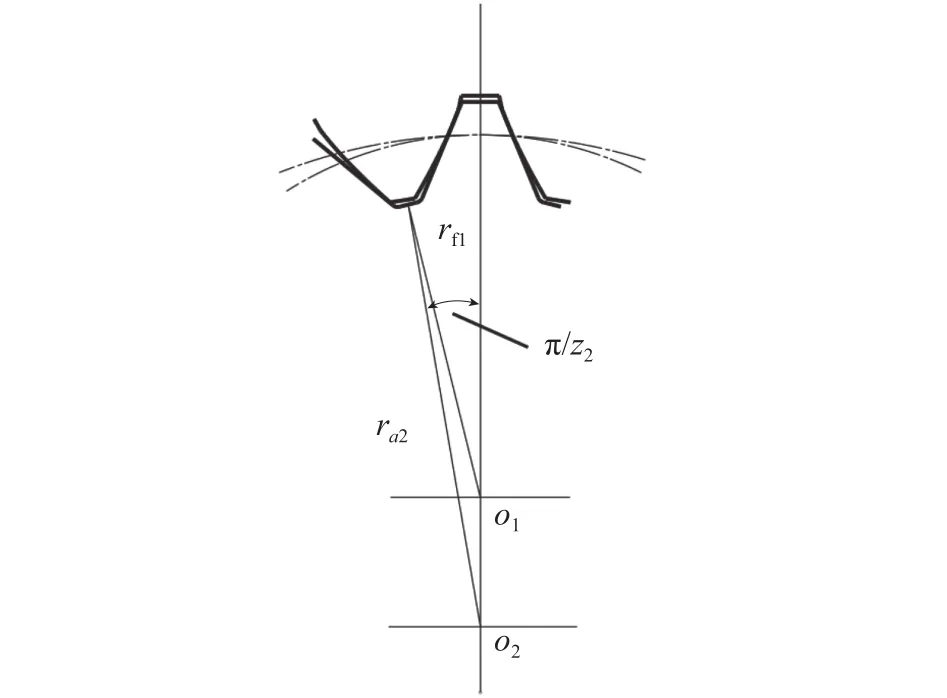
图 11 内齿圈齿顶圆的近似计算Fig.11 Approximate calculation on the crown circle of the internal ring gear

比较式（15）与式（16）中内齿圈齿顶圆半径ra2大小，并设其最大者为ra2max，则可得内齿圈齿顶圆半径ra2的取值范围为从而得到齿顶高系数取值范围，得出内齿圈齿顶高系数与重合度的关系如图12所示。

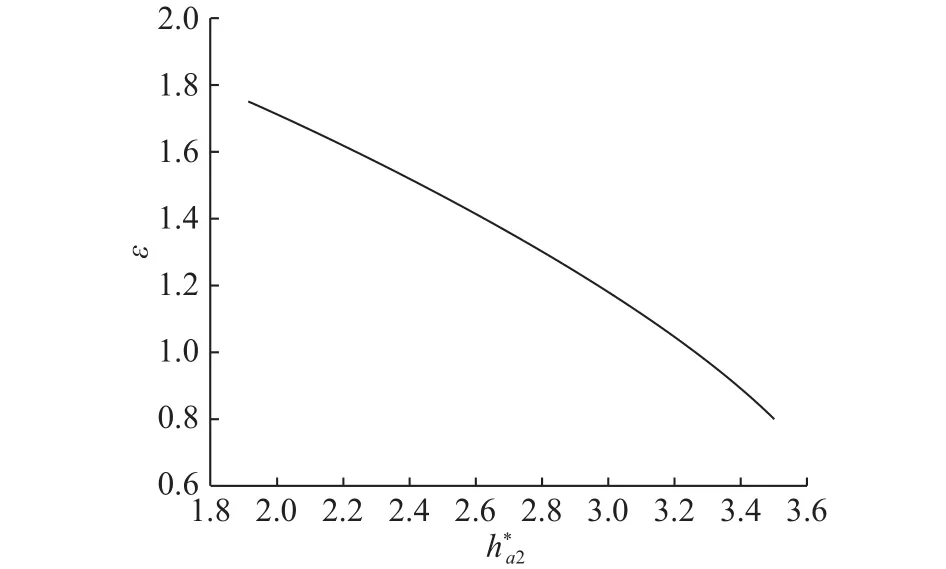
图 12 与ε的关系Fig.12 Relationship between and ε

5.3 压力角α的大小对重合度ε的影响

压力角α可以根据式（3）与齿形半角β的关系来确定。由于外齿轮齿形半角β的取值直接决定齿轮啮合传动会不会出现旋轮线的干涉现象，因此，必须要考虑到齿形半角β的取值范围，使其保证齿轮在啮合传动过程中不产生旋轮线的干涉[7]。

一方面，齿形半角β的取值范围可以根据外齿轮中心到轮齿齿廓一侧直线的距离L确定；另一方面，齿形半角β的取值范围可由外齿轮齿顶圆半径ra1的大小确定。由式（12）和式（15）可得

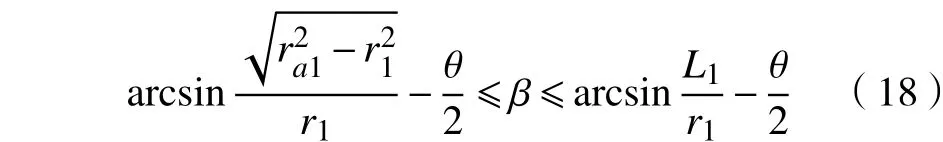
其中

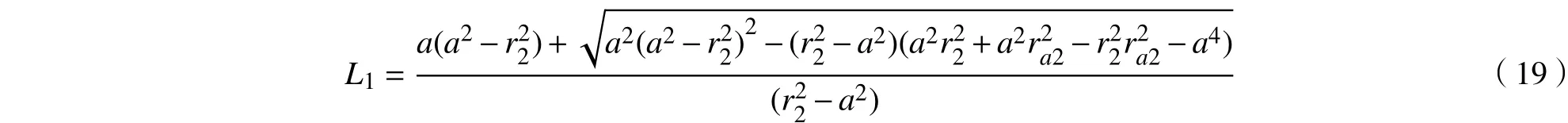
式中，L1为L的最大值。

此外，则要考虑到外齿轮齿顶圆半径ra1是随着齿形半角β的增大而减小的，如图13所示，当齿形半角β增大到某一值时，考虑到ra1的极限情况，即ra1≤o1A，此时有

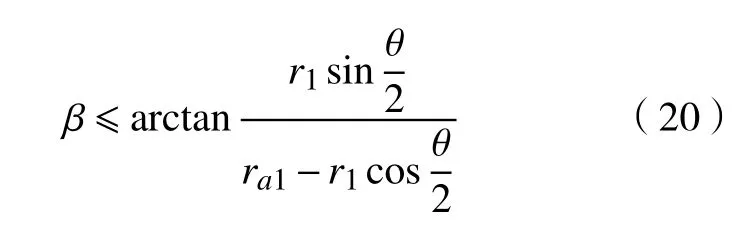
则可得外齿轮齿形半角β的取值范围为

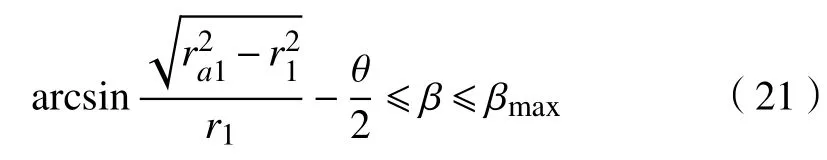
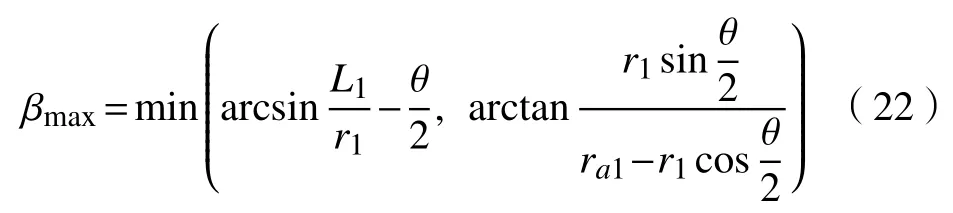
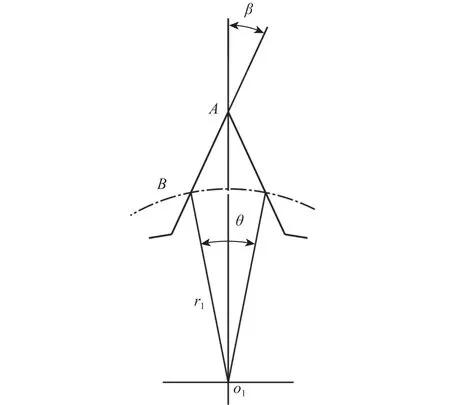
图 13 外齿轮齿顶部分几何关系Fig.13 Geometry relation of the addendum part of the external gear

从图14中可看出，随着压力角α的增大，重合度ε在逐渐减小。为保证齿轮传动能够连续平稳地运行，压力角α范围大约在20～25°。

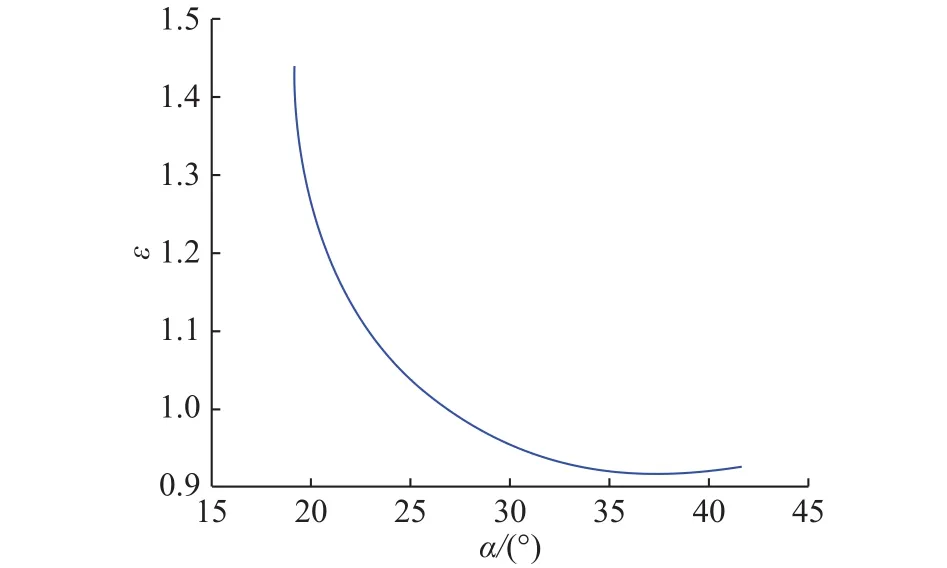
图 14 α与ε的关系Fig.14 Relationship between α and ε

6 结 论

a. 根据齿轮啮合原理，可以得到一对共轭曲线，构成了直线共轭内啮合齿轮副的齿形，并得出重合度的计算公式，通过重合度的计算公式可以确定重合度的影响因素为外齿轮的齿顶圆半径ra1，内齿圈的齿顶圆半径ra2和距离L等，为齿轮泵稳定连续工作齿轮参数的选择提供一定的理论依据。

b. 重合度随着外齿轮齿顶高系数的增大而增大，但当外齿轮齿顶高系数增大到一定值后重合度会急剧增加，对于本文所用齿轮副，当外齿轮齿顶高系数在0～0.35之间，重合度与齿顶高系数成正比；而当齿顶高系数大于0.35时，重合度急剧增加，重合度过大会引起困油现象。

c. 随着内齿圈齿顶高系数的增加，重合度逐渐减小，改变外齿轮齿顶高系数对重合度的影响比改变内齿圈齿顶高系数对重合度的影响要大。

d. 随着压力角的增大，重合度在逐渐减小，对本文所用齿轮副，为了保证齿轮能平稳地传动，压力角应该选择在15～27°之间。