基于简正波分解的不同阵列匹配场定位性能分析∗

贾雨晴1)2)3) 苏林1)2) 郭圣明1)2) 马力1)2)

1)(中国科学院水声环境特性重点实验室,北京 100190)2)(中国科学院声学研究所,北京 100190)3)(中国科学院大学,北京 100049)(2018年1月17日收到;2018年5月15日收到修改稿)

1 引 言

匹配场声源定位是水声学研究中的经典问题,近年来又成为国内外关注的热点[1−6].匹配场处理[7](matched field processing,MFP)利用声场模型计算得到阵接收声场的幅度和相位,形成拷贝声场向量,再与从实际阵接收数据中分析得到的接收声场向量进行相关处理[8],实现声源定位、环境参数估计.MFP充分利用了水声信道多途传播特点,属于一种广义的波束形成技术.

近几十年来,利用垂直阵、水平阵的匹配场声源定位方法已经得到了深入研究[9−14].垂直阵不仅是理论分析和仿真定位的起点,而且在实际实验中也是最容易实现的,因此水声实验主要选择垂直阵作为声接收阵.对于全海深布放的垂直线列阵,环境无失配时可以较好地分辨目标的深度信息和距离信息;而在无指向性水听器阵且不存在阵倾斜的情形下,垂直阵几乎没有方位分辨能力.垂直阵的定位性能受其孔径的影响,而阵列孔径被海深严格限制,在实际应用中局限较大.在定点实验中,垂直阵的系留布放形式通常会造成阵倾斜,从而使定位性能下降.对于水平阵,它具有良好的方位分辨能力,并且对位于端射方向的声源可以实现深度和距离的定位,但对于其他方位的声源,特别是正横方向的声源,定位性能大大降低,并且在满足基阵孔径和阵元数要求的前提下,浅海中海底水平线列阵的匹配场定位性能优于其他深度水平线列阵[15].传统的单一阵列形式受限于阵列的局限性,无法同时观测到目标的方位和位置信息,要么无法分辨同一方位附近不同距离的目标,要么深度分辨力较低,对于目标定位造成困难.基于实际试验的要求及现今中低频的探测定位需求,必须提高阵列探测性能,提高定位准确度,因此,综合利用多种阵形的定位优势,设计多种组合线列阵是必要的.

由于海洋环境复杂多变、实验设备布放困难等多种原因,传统的多阵列定位方法无法直接应用于海洋环境.近年来,国内外学者对组合阵形进行了较多的研究,并进行了理论仿真及实验研究,充分证明了组合阵列在水声领域的发展前景.其中最著名的实验是2000年美国国防部先进研究计划署(DARPA)立项实施的宽容被动声纳(RPS)项目,该项目在Santa Barbara水道进行实验,使用了五条均匀垂直阵,构成了一个底部边长为136 m的正五边形体[16],基于该实验,Tracey等[17]以及Zurk和Ward[18]采用自适应MFP技术,在存在水面干扰情况下,能够有效分辨水面和水下声源,对浅海运动目标进行三维定位.彭水等[19]研究了L形阵、U形阵和直线阵的MFP模型,揭示了阵形与定位性能之间的内在规律.Ge等[20]研究发现Γ形阵能够达到更好的定位.刘凤霞等[21]研究了螺旋线阵(double spiral line array,DSLA)的声源三维定位方法,利用垂直孔径和水平孔径同时估计声源方位、距离和深度,并采用宽带中频信号来提高短DSLA定位的可靠性.郑胜家[22]针对水下目标定位问题,提出了基于MFP的分布式多阵列三维定位方法,采用线性最小二乘算法对水平方位定位结果进行修正,并以各节点的目标定位深度均值作为目标深度估计,实现水下目标的三维定位.王学志等[23]通过声源穷举搜索实现三维定位,研究了声压、振速不同组合的定位性能.

分布式多阵列探测系统利用多个节点增加空间采样,能够增加目标定位的可靠性[24];此外,运用组合阵形进行目标定位可以利用不同阵形间的协同作用,实现对目标的三维定位.然而,对于组合阵形各子阵参数的选取还没有具体的研究.本文针对水下目标被动定位问题,提出了一种基于组合阵形的定位方法,通过对组合阵形接收到的声场做简正波分解,并对所得到的简正波分解矩阵进行分析,设计不同阵形对声源目标进行定位,着力提高实际实验环境下的定位性能,并降低实验设备布放难度.仿真结果表明,如果其中一个子阵对简正波分解效果较差,就会影响到最终定位效果.因此,在实际应用中,组合阵列的长度、阵元等参数的选取尤为重要.

2 垂直阵的简正波分解矩阵与阵形设计

记垂直接收阵的N个阵元位于(rn,zn),rn≡(xn,yn),n=1,2,···,N; 目标声源位于(rs,zs),rs≡(xs,ys).对于间距均匀的垂直线阵(vertical line array,VLA),阵元位置可以写成

其中dn=(n−1)Δ,Δ是阵元间距.记接收声(压)场向量为

其中ω=2πf是角频率,上角标“T”表示向量的普通转置,为了得到列向量的形式.在水平均匀的海洋环境中,接收声场向量元素可以写成简正波叠加的形式,

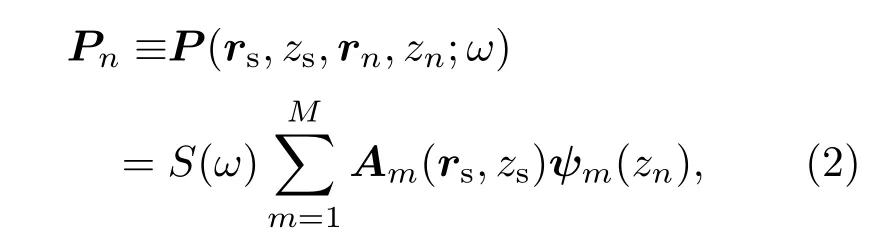
其中S(ω)是声源发射信号频谱,注意|rs−rn|=rs=|rs−r0|,

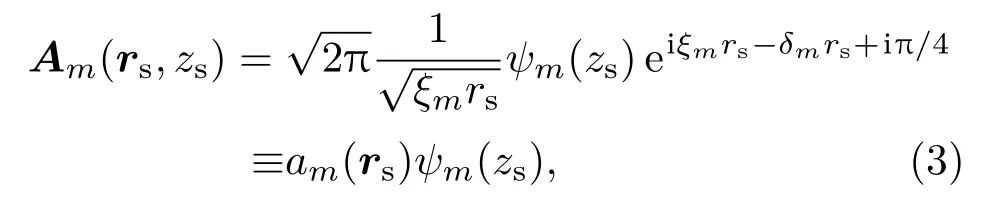
ξm,ψm(z)和δm分别是简正波本征值、本征函数和衰减系数,它们原则上也是频率的函数;M是对接收声场有显著贡献的简正波最高阶数.以传统的Bartlett线性处理器为例,归一化的匹配场定位模糊度函数为

其中Pr(r,z;ω)≡(Pr1,Pr2,···,PrN)T为拷贝声场向量,上角标“H”表示向量或矩阵的转置共轭,归一化系数为

(r,z)是假设的目标声源空间位置,当它与真实的目标声源位置(rs,zs)一致时,定位模糊度函数取最大值,从而确定出目标声源位置.用矩阵方程形式表示为

其中|r−rn|=r=|r−r0|,

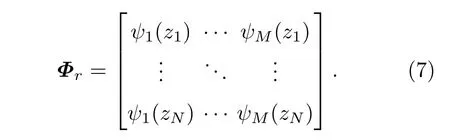
类似地,可以得到接收声场向量表示形式

形式上已经忽略了声源信号频谱项.注意不考虑失配影响时,Φ和Φr是完全一样的.这样归一化的匹配场定位模糊度函数可以重新写为

记

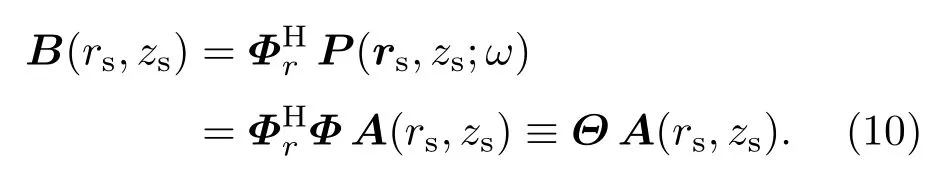
对应从阵接收声场中分解得到的简正波系数矩阵,则(9)式可以写为

注意到简正波本征函数的正交特性,在阵元足够多(满足积分离散求和近似要求)的情况下,有即简正波分解矩阵近似为对角占优矩阵甚至单位矩阵,从而能够提供尽可能多阶数和准确度的简正波分解结果,进一步支撑匹配场定位及其目标空间位置分辨.可以预见,模型计算得到的简正波系数与测量数据分解得到的简正波系数越相似,模糊度函数主瓣峰值越高,目标声源位置指示越明显;另一方面,能够正确分解得到的简正波阶数越多,主瓣宽度越小,主旁瓣峰值比越大,定位的分辨率越好.

从(10)式还可以发现,垂直线阵的简正波分解性能,实际上与阵形空间上简正波本征函数的正交性程度密切相关,利用了简正波垂直驻波场结构特征.对于布满整个水层的“满阵”情形,由于垂直接收阵最大程度地进行了简正波本征函数采样,也就最容易满足本征函数的正交性,简正波分解矩阵最接近满秩的单位矩阵,能够最大程度地区分开不同阶数的简正波.定义指标因子

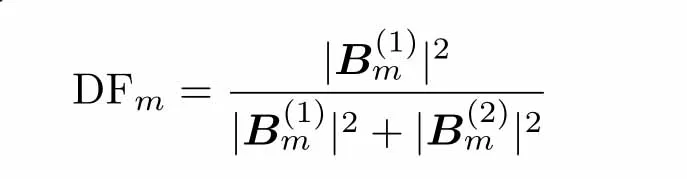
或

可以看到,对于第m阶简正波,指标因子越接近1或0 dB,分解效果越好,能够分解的简正波阶数越多,尤其是那些对远距离声场有显著贡献的简正波成分,最终的匹配场定位效果就越好.

接下来通过一些典型的数值计算示例,从简正波分解矩阵特性方面来具体分析垂直阵定位性能,说明所需要的阵形设计.数值计算仿真采用如图1所示的水平均匀浅海信道,海深100 m,声源位置距离7.5 km、深度50 m,声速剖面为典型的线性负梯度剖面,海面和海底附近声速分别为1500和1480 m/s.海底采用两层介质模型:介质密度为1.75 g/cm3,声衰减系数为0.35 dB/λ;沉积层厚度10 m,上界面声速为1600 m/s,下界面声速为1750 m/s;基底层为半无限空间,声速为1750 m/s.

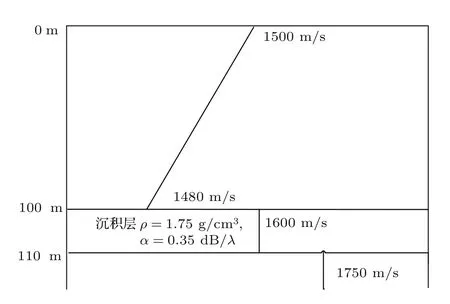
图1 海洋环境模型Fig.1.Ocean environment model.

图2给出了不同长度垂直阵的简正波分解矩阵取值分布情况,其中计算频率250 Hz,有11阶波导简正波,阵长从接近满阵的98 m变化到略小于半阵的44 m.从图2可以看出,阵长的减小使得简正波分解矩阵的对角化特征逐渐消失(对应简正波分解效果逐渐降低),但低阶简正波对应的贡献仍然保持在相当的水平上,显著大于其他阶次简正波的贡献.这是因为在负梯度声速剖面情况下低阶简正波一般局限在海底附近深度的水层范围,只需要比较短的接收阵就可以满足“充分采样”的要求.

图2 不同长度垂直阵的简正波分解矩阵取值分布情况 (a)垂直阵布放范围1–99 m;(b)垂直阵布放范围15–89 m;(c)垂直阵布放范围15–79 m;(d)垂直阵布放范围15–69 m;(e)垂直阵布放范围15–59 mFig.2.The value of mode decomposition matrices with different length of VLA:(a)VLA laying range 1–99 m;(b)VLA laying range 15–89 m;(c)VLA laying range 15–79 m;(d)VLA laying range 15–69 m;(e)VLA laying range 15–59 m.

表1为不同长度垂直阵简正波分解矩阵的特征值分布情况.从表1可以看出,由于阵长的减小,部分特征值已经从“满阵”时的接近于1变到了接近零的程度.小特征值的出现说明接收阵的简正波分解性能已经明显下降,也会导致匹配场定位性能的下降.

表2给出了50 m阵长的“半阵”垂直阵布放在不同水层深度范围时简正波分解矩阵的特征值分布情况.图3为50 m阵长“半阵”垂直阵的简正波分解矩阵取值分布情况,其中计算频率250 Hz,有11阶波导简正波.可以看到,垂直阵位于较深处时小特征值数目略微增加,意味着对于负梯度声速剖面情形,“半阵”布放于上半层水域可能易于得到较好的定位效果.

从上述典型浅海环境的计算结果可以看到:采用垂直线阵进行定位,一般要求阵长接近满阵水平,至少要超过“半海深”长度.

表1 不同长度垂直阵的简正波分解矩阵特征值分布情况Table 1.Eigenvalue distribution of mode decomposition matrices with different length of VLA.

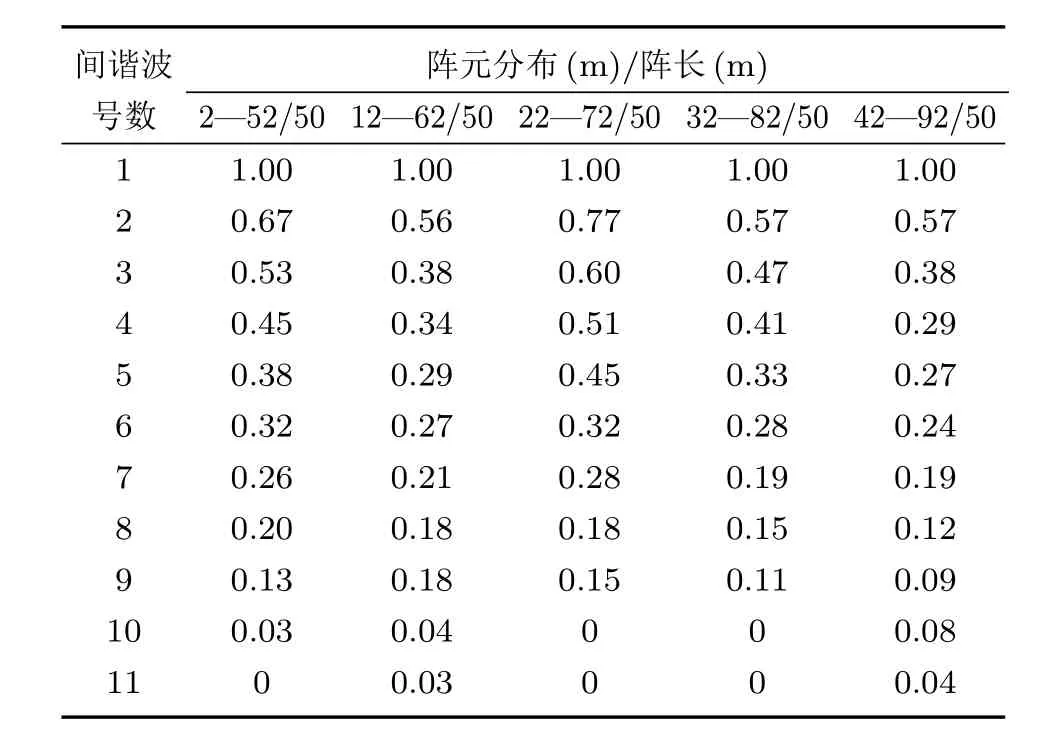
表2 给定长度垂直阵不同布放深度时分解矩阵特征值分布情况Table 2.Eigenvalue distribution of mode decomposition matrices with the same length of VLA.

图3 相同长度垂直阵的简正波分解矩阵取值分布情况 (a)垂直阵布放范围2–52 m;(b)垂直阵布放范围12–62 m;(c)垂直阵布放范围22–72 m;(d)垂直阵布放范围32–82 m;(e)垂直阵布放范围42–92 mFig.3.The value of normal wave decomposition matrices with same VLA length:(a)VLA laying range 2–52 m;(b)VLA laying range 12–62 m;(c)VLA laying range 22–72 m;(d)VLA laying range 32–82 m;(e)VLA laying range 42–92 m.

3 水平阵的简正波分解矩阵与阵形设计

对于间距均匀的水平线阵(horizontal line array,HLA),假设沿平行y轴方向布置,阵元位置为

其中Δrn=dncosφ.类似地,可以得到接收声场向量表示形式

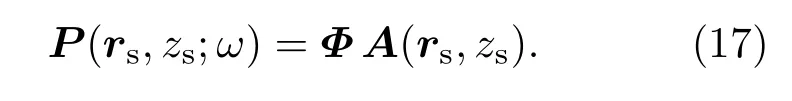
注意不考虑失配影响时,Φ和Φr是完全一样的.这样归一化的匹配场定位模糊度函数可以重新写为

记

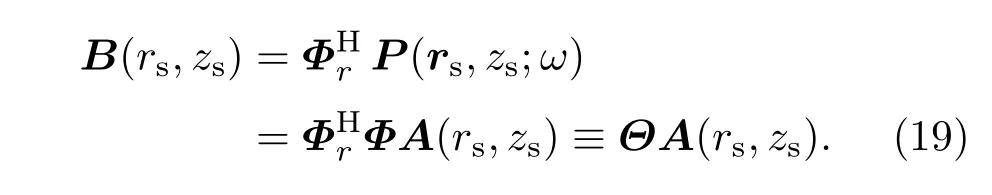
对应从阵接收声场中分解得到的简正波系数矩阵,则(18)式可写为

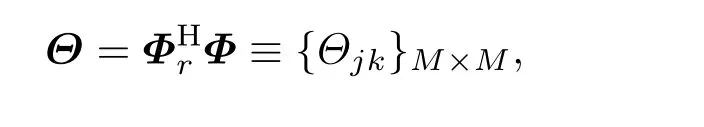
可以看到,与垂直阵不同,水平阵简正波分解实际上利用的是简正波声场在水平方向上的行波场特性,形式上类似平面波波束形成.水平线阵的角度分辨率越高,简正波分解矩阵越接近对角占优矩阵甚至单位矩阵,从而能够提供尽可能多阶数和准确度的简正波分解结果,进一步支撑匹配场定位及其目标空间位置分辨.可以预见,目标偏离正横方位时,等效的水平阵孔径越大,越有利于简正波分解.

图4给出的是不同长度的水平线阵简正波分解矩阵取值分布情况,海洋环境模型如图1所示,水平阵阵长从100 m到2000 m(相当于1倍海深到20倍海深)变化.当阵长大于500 m时具有较为明显的单位矩阵特征,随着阵长的减小,分解矩阵的对角化特征逐渐减弱,对应简正波分解能力以及定位能力下降.

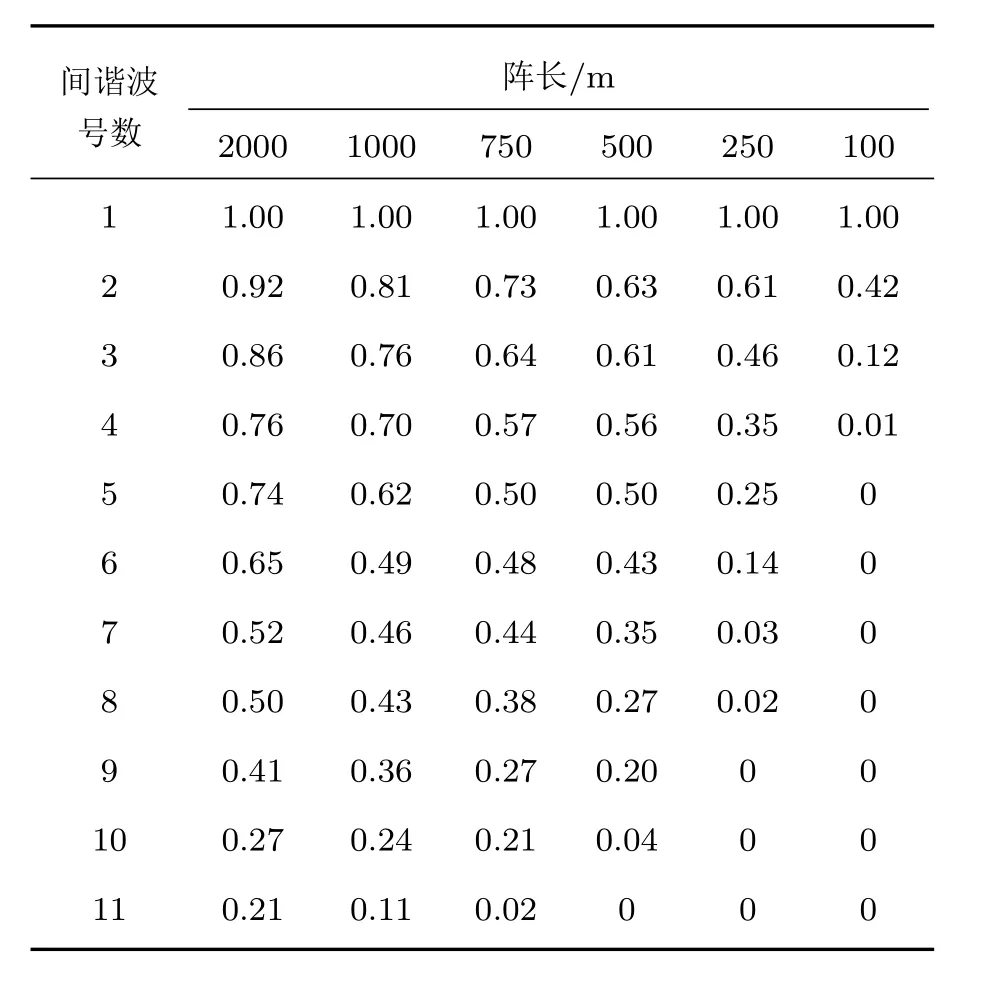
表3 不同长度水平阵的简正波分解矩阵特征值分布情况Table 3.Eigenvalue distribution of mode decomposition matrices with different length of HLA.

表3为不同长度水平阵对应的分解矩阵特征值分布情况.与表1相比,从分解矩阵特征值的分布和变化情况来看,并没有发现其大小同各阶简正波的贡献有明显的对应关系.简正波分解在水平方向上利用的是“行波场”特征而非深度方向上的“驻波场”特征,这样短垂直阵可以利用低阶简正波本征函数局部区域分布特点来进行有效区分.从简正波分解矩阵计算(21)式来看,水平线阵的高阶简正波部分更容易满足单位矩阵的要求,使得分解矩阵具有局部单位矩阵的结构特点.由表3可以看出,随着水平阵长的减小,分解矩阵的部分特征值逐渐变小,当阵长小于500 m后,小特征值急剧增多,个别特征值甚至变为零,因此也无法进行有效的目标定位.

综上所述,如果采用水平线阵,目标在最有利的端射方向时一般要求6倍海深以上,偏离端射方向时要求的阵长还会增加,例如偏离45°时,大致需要端射方向的1.5倍阵长.

图4 不同长度水平阵的分解矩阵取值分布情况 (a)阵长2000 m;(b)阵长1000 m;(c)阵长750 m;(d)阵长500 m;(e)阵长250 m;(f)阵长100 mFig.4.The value distribution of mode decomposition matrices with different HLA length:(a)Length 2000 m;(b)length 1000 mm;(c)length 750 mm;(d)length 500 m;(e)length 250 m;(f)length 100 m.

4 水平阵和垂直阵的组合阵形

多条阵的组合阵形可以对空间进行大范围的声场采样,通过将不同位置的阵列作为一个超大孔径的多位基阵,获得更高的空间分辨力.记L个子阵对应的接收声场向量和拷贝声场向量为

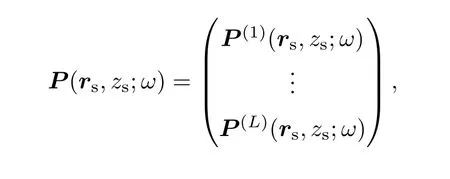
这样,传统的匹配场处理(CMFP)输出结果为

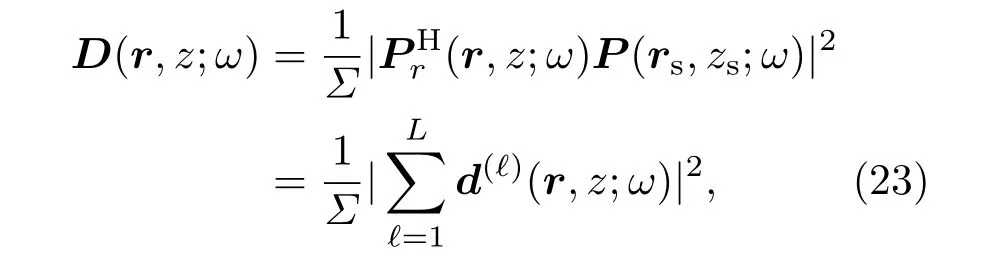
其中

各个子阵的定位模糊度函数为

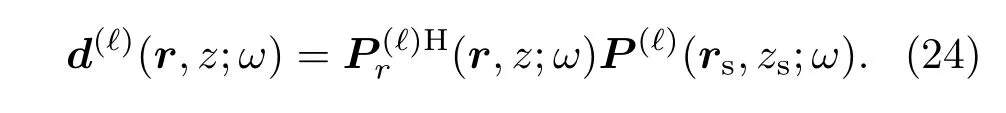
注意(23)式给出的是阵间非相干匹配场处理的形式,最大程度地利用了多个子阵提供的空间差异性.工程实际中也可以根据具体情况考虑阵间相干匹配场处理的形式

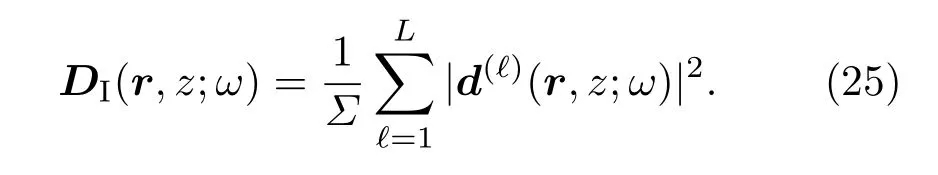
对于(23)式,进一步分析可知,

记

对应从阵接收声场中分解得到的简正波系数矩阵,则(26)式可写为

从以上可以看出:1)组合阵形的定位函数D(r,z;ω), 是单子阵定位函数d(ℓ)(r,z;ω)的加权求和形式,由于归一化因子项Σ的影响,权系数比重较小的子阵贡献很容易被“掩盖”;2)从简正波分解效果来看,组合阵形的分解结果仍然是子阵分解结果的加权求和形式,如果其中某一子阵的简正波分解能力差,但权系数比重大,就会影响到总体的分解效果.

如果直接从简正波分解的角度来看,组合阵形对应的简正波分解矩阵为

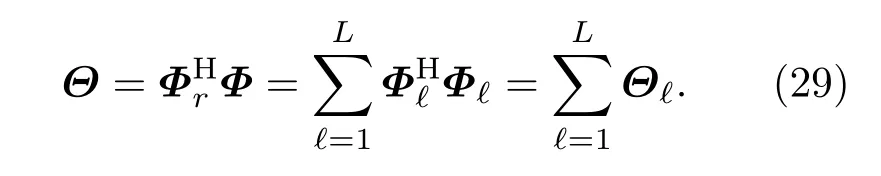
简正波分解矩阵Θ的矩阵元表达式为(30)式,组合阵形分解结果为(31)式:

由(30)式和(31)式易知,组合阵形的总阵分解结果,是各子阵单独进行简正波分解后,分别通过矩阵项进行修正的结果.原则上只要简正波分解矩阵Θ是满秩的,就可以有比较好的简正波分解效果以及进一步的定位效果,不论各个子阵对应的分解矩阵是否满秩.

对于CMFP而言,需要从模糊度函数的角度来进行分析,

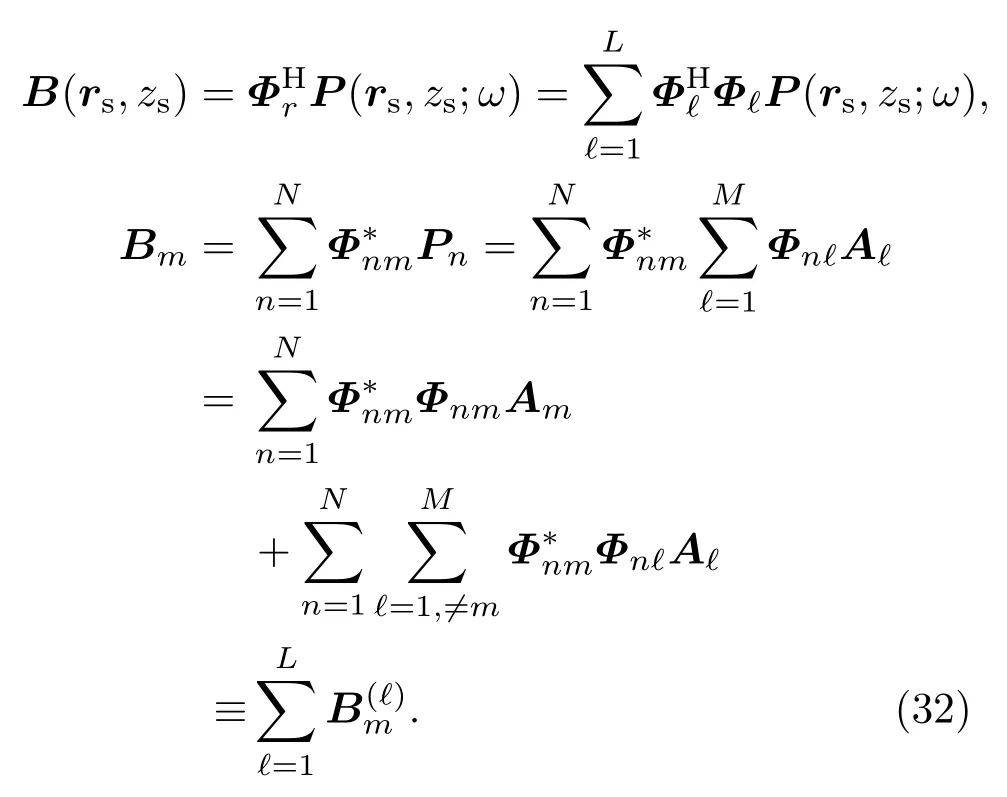
可以看到,组合阵形的模糊度函数由各子阵的模糊度函数叠加获得,因此,如果其中一个子阵对简正波分解效果较差,反而会影响到最终定位效果.

5 组合阵形定位性能仿真分析

对单个垂直阵或者单个水平阵的分析结果表明,节点基阵的设计应该兼顾垂直和水平孔径,综合垂直阵和水平阵两种阵形的目标探测和定位优势,充分利用水平阵的方位分辨能力和垂直阵的距离、深度分辨能力,两者结合以提高对水下目标的分辨和探测能力,并运用于水下目标探测定位和水面、水下目标的分辨.

典型的组合阵形有L形阵、垂直线阵+十字阵、垂直阵+环形阵、立体阵、多个垂直阵或水平阵等,这一部分将通过数值计算示例来分析组合阵形的目标探测和定位性能.

为了定量评估匹配场定位结果的优劣并进行比对分析,本文引入主旁瓣比[25](peak to sidelobe ratio,PSLR)作为衡量定位性能的参数,定义PSLR为主瓣峰值与最大旁瓣峰值的比值,旁瓣峰值会对临近点的目标产生干扰,这样强目标附近的弱目标就会被旁瓣掩盖.因此,PSLR越大,定位性能越好、准确度越高.

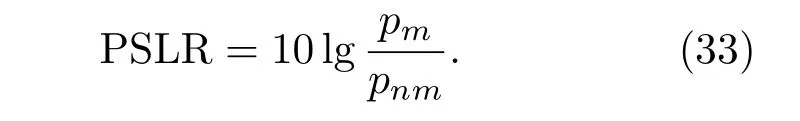
本文研究的组合阵形主要是L形阵,L形阵由一条垂直线阵和一条水平线阵组成,如图5所示,垂直阵布放在水平阵的一端,并将该端水平阵上第一个阵元作为参考阵元.为了简化计算过程,认为已经通过水平阵估计得到了目标方位值,从而主要是对目标距离和深度进行估计.

图5 L形阵布放示意图Fig.5.L-shaped array model.

数值计算仿真中,首先进行单一垂直阵(长阵)与L形阵定位性能的对比,假设垂直阵布放在26.5到73 m深度范围,阵元间距1.5 m,阵元数为32;水平阵为64元均匀线列阵,阵元间距1.5 m,布放在海底;声源位置距离3 km,深度30 m,海深80 m,声速剖面为均匀层,海洋环境如图6.当仅使用垂直阵部分进行定位时,得到的模糊度表面如图7所示,距离和深度定位准确度均为100%.将L形阵的垂直与水平阵部分都加以利用,当目标位于水平阵的端射方向时,得到的定位模糊度表面如图8所示.由图8可以清楚地看到,增加水平阵后,在水平阵端射方向旁瓣增加得较为明显,增加了次高峰,但深度定位准确度仍为100%,距离定位准确度有微小偏差,准确度为99.33%.

图6 海洋环境信息Fig.6.Ocean environment.

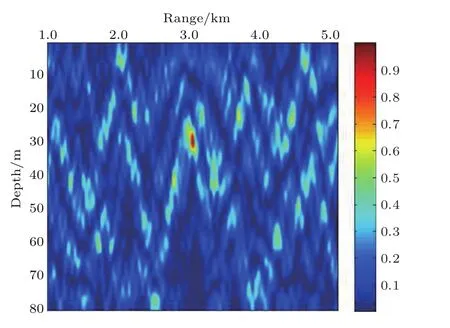
图7 单垂直阵(长阵)的定位模糊度表面Fig.7.Localization ambiguities surface of VLA.

图8 目标位于端射方向时L形阵的定位模糊度表面Fig.8.Localization ambiguities surface of L-shaped array when the target is located in end fire phase.

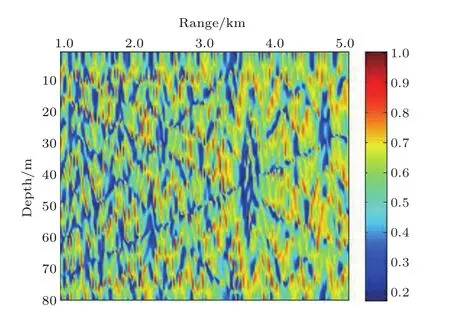
图9 目标位于端射方向时单水平阵(64元)的定位模糊度表面Fig.9.Localization ambiguities surface of HLV(array element is 64).

需要指出的是,由于仿真所使用的水平阵阵长较短,即便是目标在水平阵定位最有利的端射方向上,单独使用水平阵部分也很难进行目标定位.仅使用水平阵进行定位仿真的模糊度表面如图9所示,无法准确进行定位.在组合阵形定位中,增加短水平阵主要是为了增加方位分辨能力以及对旁瓣性能的改善.当使用L形阵进行定位时,得到的模糊度表面如图10所示,分别仿真了当目标位于水平阵端射方向、与水平阵夹角为30°,60°及正横方向的情况.

图10 L形阵(垂直阵为32元)定位模糊度表面图 (a)目标位于端射方向;(b)目标位于30°方向;(c)目标位于60°方向;(d)目标位于正横方向Fig.10.Localization ambiguities surface of L-shaped array(array elements of VLA is 32):(a)Target is from end fire;(b)target is from 30°;(c)target is from 60°;(d)target is from 90°.

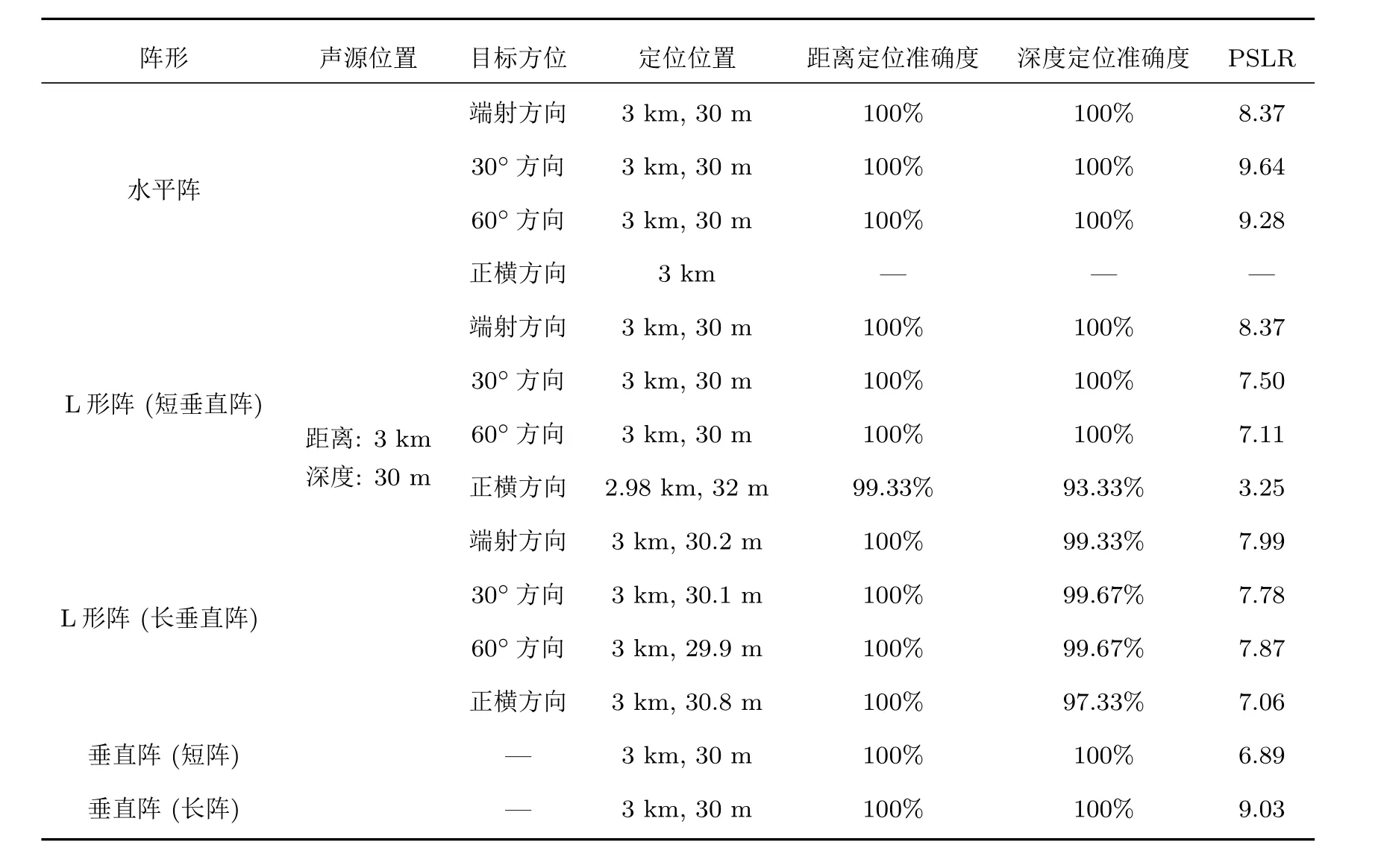
表5 不同阵形定位性能的比较Table 5.Comparison of different positional performances.

通过表5可以看出,在垂直阵阵元固定的情况下,增加一个水平阵更便于分辨不同方位的声源位置,但当目标位于水平端射方向时,可以明显地看出L形阵CMFP模糊度表面的旁瓣较高,PSLR较小,在30°及60°方向上,L形阵的PSLR与单一水平阵相比,有大幅度减小.表5中垂直阵(长阵)为32元垂直阵,布放深度接近全海深,可以看出,即使在定位性能最好的L形阵的端射方向,其PSLR也比垂直阵(长阵)的小,即定位性能较差.由此可知当某一子阵定位性能即简正波分解能力差时,会影响到组合阵形的定位性能.这种现象在垂直阵(短阵)和水平阵组合定位时却有着相反的结论,即垂直阵(短阵)的定位PSLR小于L形阵PSLR.下面对垂直阵(短阵)和L形阵做具体分析.

考虑到实际海上实验的困难,相较于全海深垂直阵而言,短垂直阵在浅海实验中使用更为频繁,更为直接.因此接下来对短垂直阵进行进一步研究,设定短垂直阵布放在6.5—29 m深度范围,阵元间距1.5 m,阵元数为16,对单短垂直阵进行定位仿真,海洋环境如图8,得到的模糊度表面如图11所示.可以看到,由于只有垂直阵,阵长较短、有效孔径较少,尽管能够正确定位目标,但其旁瓣比较高,定位性能较差.垂直阵(长阵)、垂直阵(短阵)及L形阵的具体定位性能比较如表5所列.

图11 单垂直阵(短阵)的定位模糊度表面Fig.11. Localization ambiguities surface of VLA(short array).

将L形阵的垂直阵(短阵)与水平阵部分都加以利用,当目标位于水平阵端射方向时,得到定位模糊度表面如图12(a)所示,与单独使用垂直阵(短阵)相比,旁瓣得到有效抑制.图12(b)和图12(c)是目标位于水平阵30°和60°方向的定位结果,随着目标逐渐偏离端射方向,尽管主瓣变化不明显,但深度和距离估计的旁瓣不断升高,目标在正横方向时,定位效果最差,但仍可进行定位,此时模糊表面如图12(d)所示.

图12 L形阵定位模糊度表面图(垂直阵为16元) (a)目标位于端射方向;(b)目标位于30°方向;(c)目标位于60°方向;(d)目标位于正横方向Fig.12.Localization ambiguities surface of L-shaped array(array elements of VLA is 16:(a)Target is from end fire;(b)target is from 30°;(c)target is from 60°;(d)target is from 90°.

从简正波分解矩阵的角度来解释以上现象,分别对垂直阵(短阵)和L形阵的端射方向所接收到的声场做简正波分解,分解矩阵特征值的分布情况如表6所列,图13为两种阵形简正波分解矩阵取值分布情况.由表6可以看出,虽然两种阵形的小特征值均较多,但垂直阵(短阵)的简正波分解矩阵特征值更快接近“0”值,代表着在相同的海洋环境中,使用垂直阵(短阵)进行定位更容易“失配”.从简正波的角度进行分析,垂直阵的简正波对垂直方向上的分量更为敏感,会在某些特征值上达到次高峰的效果,而水平阵引入了与本征值相关的e指数形式,使其在特定深度上的敏感度要高于单一垂直阵,从而达到抑制旁瓣的效果,造成模糊度函数表面上的旁瓣较低,PSLR有所提升的现象.

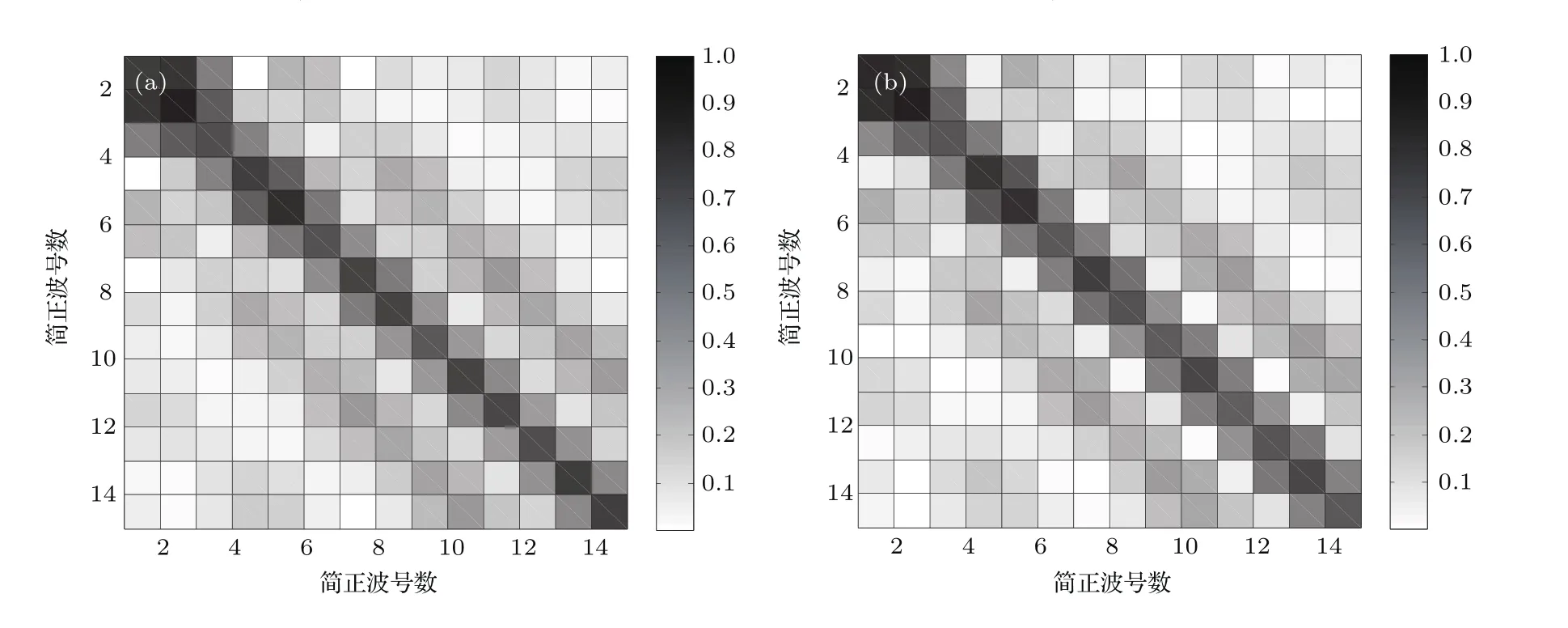
图13 不同阵形的简正波分解矩阵特征值分布情况 (a)垂直阵;(b)组合阵形Fig.13.The value of mode decomposition matrices with different arrays:(a)VLA;(b)combined array.

表6 不同阵形的简正波分解矩阵特征值分布情况Table 6.Eigenvalue distribution of mode decomposition matrices of different array.

虽然组合阵形可以实现目标的三维定位,增加方位信息,提高定位的可靠性,但在理论上没有提高,在某些情况还会使定位性能下降,目标定位准确度的提高也不大,因此确定组合阵形的相关参数,如阵长、阵元数等尤为重要.在实际应用中,满阵垂直阵布放较为困难,且易受到环境影响,增加定位难度.短阵布放较为简单,更适用于实际的定位实验.而对于水平阵,常见的布放方式为坐底布放和拖曳布放,增加了实验的可机动性和使用范围.对于短垂直阵和短水平阵的组合可以降低布放实验设备的难度,在某些情况下也可以达到长垂直阵的定位精度,在获得目标方位信息的基础上,增加了实验设备的选择空间.

对于双声源及复杂声源位置的情况,尽管长水平线列阵及长垂直线列阵可以确定声源的深度信息,但长水平线列阵的布放在实际操作中是很困难的,而且若考虑到平面波波束形成的要求,阵元间距要小于1.25 m,需要上百个阵元,这无疑带来巨大的实验成本.基于实际应用的考虑,组合阵无疑是对定位性能和实验复杂度的折中选择.

6 结 论

在浅海环境下,当海洋环境及阵形等参数无失配时,基于匹配场理论的声接收阵可有效实现目标的定位,但定位性能受阵形、阵元数目等阵列参数的影响.为此,本文针对浅海环境下,基于简正波分解方法,对组合阵形的目标声源定位性能进行了研究.

对垂直阵、水平阵及组合阵形的简正波分解矩阵特征值与定位模糊度表面进行了分析,当某一子阵的简正波分解效果较差时,组合阵形的定位性能会受到很大影响,会使定位性能下降.在垂直阵阵元固定的情况下,增加一个水平阵便于获取不同方位的声源信息,但组合阵的定位性能会受增加的短水平阵影响,而有所降低.而通过短垂直阵与组合阵的比较发现,由于水平阵引入了与本征值相关的e指数形式,使其在特定深度上的敏感度要高于单一垂直阵,从而达到抑制旁瓣的效果,造成模糊度函数表面上旁瓣较低,PSLR有所提升.尽管组合阵相对于长垂直阵的定位性能有所下降,但其定位准确度均处于90%以上,若提高搜索精度,其定位准确度还会有所增加.

在实际布放时,组合阵形会在一定程度上降低布放的困难,另外,多种阵形组合可以增加目标声源的方位及深度信息,实现三维目标定位.对于目标位于水平阵非端射方向时旁瓣较强的情况,可以通过宽频带匹配场处理器进行抑制,提高定位准确度.对于组合阵,从阵间相干匹配场处理器形势来看,也可以认为是对简正波分解系数的比较,组合阵形的定位性能的优劣可以通过简正波分解矩阵的性能来判定,从而建立一种彼此之间定性甚至定量的关系.在本文仿真条件下,组合阵形的简正波分解矩阵的特征值具有明显的对角化特性,其有效特征值为5阶,占总特征值阶数30%左右.对250—1000 Hz频段进行分析,均得到相似结论,可以近似认为当组合阵形的简正波分解矩阵的有效特征阶数占总特征值阶数的30%及以上且具有明显的对角化特性时,组合阵形可以进行有效定位.以此为依据,可以选取组合阵形各子阵的阵列长度和阵元等参数.但具体的阵元数和阵间距设置尚未发现量化规律,需根据不同环境分别仿真设计.此外,对双声源及高斯白噪声环境下目标定位也有类似的结论,由于篇幅原因不再赘述.对目标位于组合阵形某一阶简正波驻点情况、子阵阵元间距等参数的选取是下一步研究的重点.