工业废水排放与经济增长关系的实证分析

章恒全，韩若祎

（河海大学 商学院，南京 211100）

0 引言

改革开放以来，我国水环境污染与经济发展的矛盾日益突出。其中，工业废水排放作为工业用水的附属消耗产品，是废水排放的重要来源[1]。根据2016年发布的《中华人民共和国国民经济和社会发展第十三个五年规划纲要》，积极倡导落实最严格的水资源管理制度，同时将大力推进污染物总量减排放在重要位置，全面实施工业污染源达标排放计划，并推进水功能区分区管理。因此，减少工业废水排放，实现经济可持续发展，是节水型社会建设的客观要求。目前，国内对于经济增长和环境污染的研究主要基于面板数据，从理论和实证方面分析二者间环境库兹涅茨曲线的存在性及适用性，并对现有理论假设进行扩展研究[2，3]。计量方法的不同导致所得出的结论具有一定差异性，考虑到面板数据计量模型在分析截面数据以及时间序列数据上的优势[4]，本文基于八大经济区域数据研究工业废水排放与经济增长之间的关系，具有重大的现实意义。

1 模型构建与数据说明

1.1 模型构建

本文基于我国31个省八大经济区域1997—2015年相关数据，以工业废水排放量和各省人均GDP为度量指标，运用一种非结构性方法来建立各变量间关系的VAR模型，研究我国各区域工业废水排放与经济增长之间的关系。本文结合我国实际情况，在具体考虑工业废水排放与经济增长的基础上，建立面板VAR模型：

其中，Yit为i省（直辖市）t年的工业废水排放与经济增长构成的向量（以1997年为基准）；p为自回归滞后阶数；βj为各面板单位的协整系数矩阵；ait为各地区不同的固定效应；ɛit为随机扰动项。

此外，本文将我国31个省按八大经济区域的分类方式进行分别研究，在验证变量序列平稳性后，通过协整分析和脉冲响应分析对我国各区域工业废水排放与经济增长之间的关系进行相关研究。脉冲响应和方差分解是VAR模型常用的分析方法，其中，脉冲响应函数描述一个内生变量对误差的反应，VAR预测方差分解法则能够给出随机信息的相对重要性[5]。

脉冲响应函数的数学定义如式（2）所示：

式中，q为冲击向量，qk为来自第k个分量的冲击，Ⅱt-1是t-1时刻的信息集，即历史运行轨迹，n为冲击响应时期数。

方差分解讨论的一般是正交化残差对预测的均方差MSE影响的比率，对于将来s期的预测误差表示为[6]：

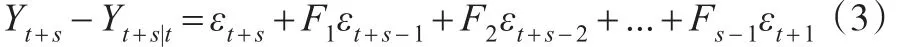
其中 Yt+s|t=E(Yt+n|Ⅱt-1)，所以：

正交分解后可得出每个变量在冲击中贡献的百分比，需注意的是，有必要排除干扰ɛt存在同期相关的情况。本文构建VAR模型，拟运用脉冲响应函数和方差分解来分析中国各区域工业废水排放与经济增长之间的相互作用和影响情况。

1.2 数据说明

本文中数据时间跨度为1997—2015年，现对变量选取情况、数据样本来源及处理进行相关说明。（1）本文采用工业废水排放量和各区域人均GDP为度量指标，并且为了剔除物价波动的影响，选择1997年为基期，将各地区人均GDP进行折算[7]；（2）鉴于研究数据的准确性和可获得性，及1997年前重庆市废水排放数据合并于四川省中，本文选取我国31个省份数据分析（不含港澳台），各年工业废水排放数据来源于《中国环境年鉴》；地区生产总值数据来源于中华人民共和国国家统计局、《中国统计年鉴》；（3）为消除异方差，本文各变量取对数化处理，按八大经济区域的分类方式分别考察。

2 实证分析

2.1 面板单位根检验

面板单位根检验，是指将面板数据中的变量各横截面序列作为一个整体进行单位根检验，它作为经济实证研究的基础，涉及到后续协整建模和误差修正分析的过程[8]。

需要说明的是，面板数据有同质型和异质型之分，对于同质型面板数据来说，假定零假设及备择假设相同；而对于异质型来说，其自回归系数均不同。因此有两类情况，一是假定所有面板单位包含相同单位根，典型检验如LLC检验 (2002)[9]、Breitung检验(2000)[10]、Hadri检验等；二是放宽条件，允许自回归系数取值不同，如IPS检验(2003)[11]、ADF检验、PP-Fisher检验等。

综合考虑后，本文在对变量工业废水排放量（lnfs）和人均GDP（lngdp）序列采取面板单位根检验时，按上面两类检验方式分别进行五项检验，得出：除了东北地区变量序列的水平值和一阶差分值无法通过单位根检验，以及长江中游地区lngdp、lnfs序列原值通过单位根检验外，其余六大经济区人均GDP和工业废水排放量序列的水平值均无法拒绝单位根的原假设，即原值序列不平稳，检验无法通过。但在对相关数据进行一阶差分处理后再次检验，剩余六大经济区各变量序列均平稳，通过单位根检验。由于协整检验分析的前提要求变量同阶单整，东北地区一阶差分值不能满足检验要求，因此予以剔除。

2.2 协整检验

本文对经济区变量数据进行分析，首先建立lngdp对lnfs序列数据回归模型，然后对各截面方程进行残差单位根检验，根据若可以显著拒绝“所有截面回归方程的残差序列都有单位根”的原假设，则证明面板数据序列工业废水排放和经济增长之间存在协整关系，分析发现，各截面残差序列平稳，不含单位根，即工业废水排放和经济增长之间存在协整关系，由于步骤重复，这里不再赘述，由最后的检验结果可知，残差序列平稳，检验值小于1%显著性水平下临界值，因此判断被检验的六大经济区的工业废水排放和经济增长之间具有长期的均衡关系，可以建立面板数据的误差修正模型。本文VAR模型所有倒数根的模都小于1，即该模型稳定，可以进行脉冲响应分析。此外，经过各项判别标准相关参数计算，模型最优滞后阶数确立为3阶。

2.3 面板误差修正模型

在协整检验通过后，依据面板误差修正模型可以进一步探讨工业废水排放和经济增长间的长期和短期动态关系（见表1）。

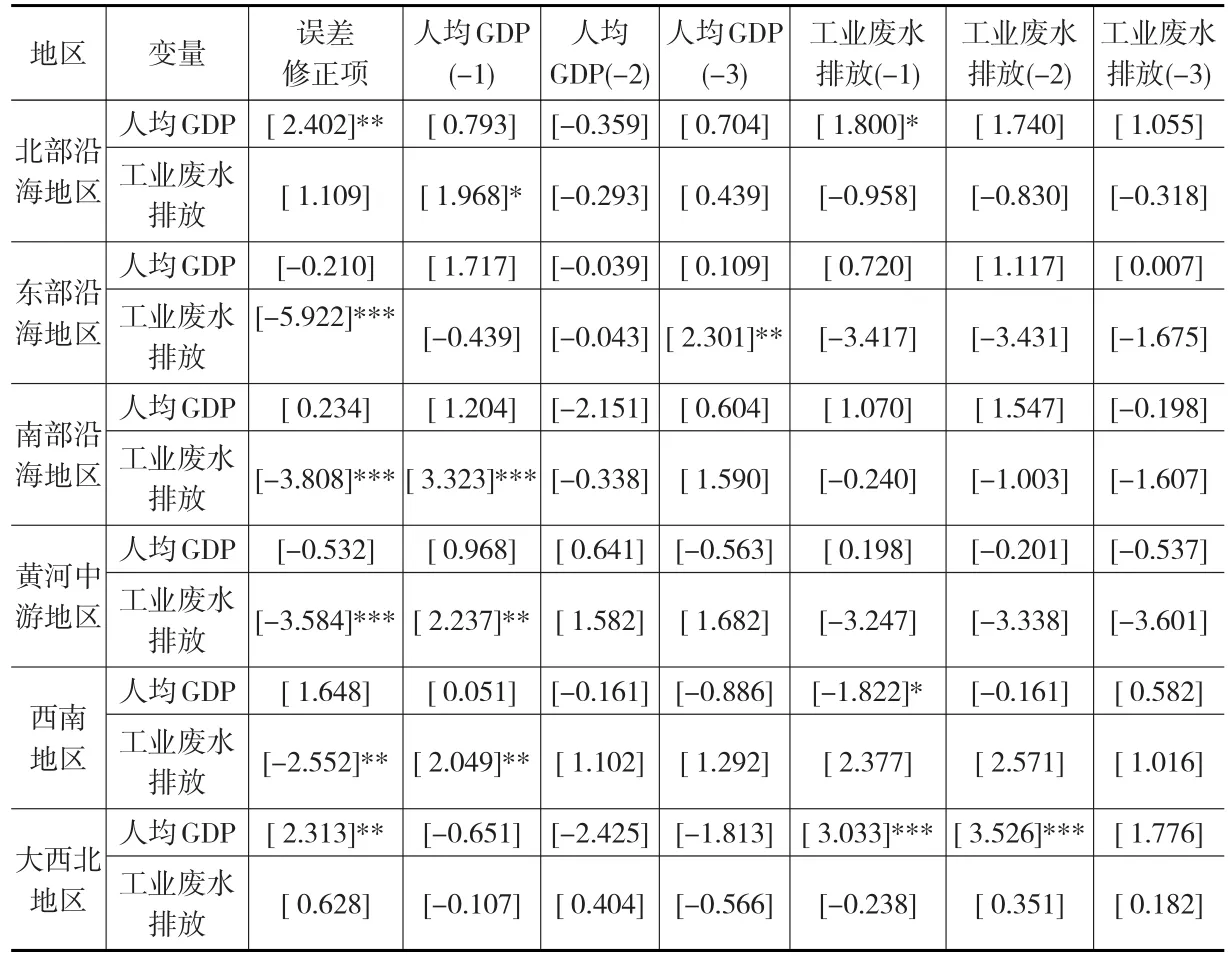
表1 面板误差修正模型结果

由表1中VEC结果可见，北部沿海地区长期存在工业废水排放到GDP的单向因果关系、短期存在工业废水排放与GDP的双向因果关系（时间调整期均为1年）；东部沿海地区长期存在GDP到工业废水排放的单向因果关系、短期内存在GDP到工业废水排放的单向因果关系（时间调整期为3年）；南部沿海地区和黄河中游地区长期存在GDP到工业废水排放的单向因果关系、短期存在GDP到工业废水排放的单向因果关系（时间调整期为1年）；西南地区长期存在GDP到工业废水排放的单向因果关系、短期存在GDP与工业废水排放的双向因果关系（时间调整期均为1年）；大西北地区长期存在工业废水排放到GDP的单向因果关系、短期内存在工业废水排放到GDP的单向因果关系（时间调整期为2年）。此外，各经济区工业废水排放与经济增长正负相关性见下页表2。

2.4 脉冲响应和方差分解

本文根据面板VAR模型，分析变量变化之间的相互影响关系，通过脉冲响应分析，观察变量对于冲击的响应情况。首先，从北部沿海地区经济增长对工业废水排放一个单位冲击的响应可知，LNGDP的当期反应值为负，然后逐步平稳下降，到第7期后处于稳定状态，整个分析期内LNFS对LNGDP的总体影响为负值，即工业废水排放的变动对区域经济发展会产生负面效应，有一定抑制作用；从北部沿海地区工业废水排放对经济增长一个单位冲击的响应可知，LNFS的当期反应值为正，在第2期达到最高值后下降，直至第7期为0，后下降至第9期达到稳定状态，表明随着区域经济增长，工业废水排放有减小的趋势，但短期经济增长会增加工业废水排放量，这与前文协整分析及区域间比较分析的结果相吻合，同理可证其余地区结论基本与前文区域间分析相符。为了更加清楚地表明各区域经济增长和工业废水排放量的相互影响程度，进行预测方差分解，分解结果见表3。

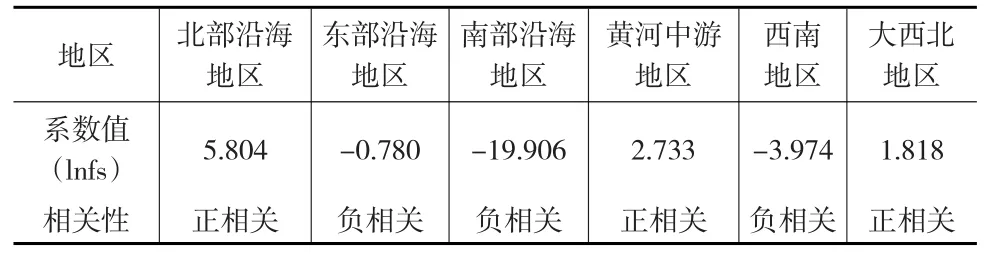
表2 面板数据模型估计

表3 预测方差分解结果

不考虑自身贡献率为前提，由表3数据易知，各经济区域工业废水排放量对人均GDP的贡献率与人均GDP对工业废水排放量的贡献率都基本维持在0～30%之间，其中，工业废水排放对经济增长影响程度从大到小排列依次为大西北地区、北部沿海地区、东部沿海地区、南部沿海地区、黄河中游地区、西南地区；经济增长对工业废水排放影响程度从大到小排列依次为黄河中游地区、东部沿海地区、西南地区、南部沿海地区、北部沿海地区、大西北地区。

3 结论与建议

本文基于我国31个省八大经济区域1997—2015年相关数据，以工业废水排放量和各省人均GDP为度量指标，运用VAR模型研究了我国各区域工业废水排放与经济增长之间的关系，得到以下结论和建议：

（1）北部沿海地区、东部沿海地区、南部沿海地区、黄河中游地区、西南地区、大西北地区的工业废水排放和经济增长之间具有长期稳定的均衡关系。

（2）各大经济区内经济增长与工业废水排放之间的相互影响存在较为明显的区域异质性。其中，经济发展最为发达的东部沿海地区与南部沿海地区经济增长与工业废水排放之间存在良性影响，随着经济的逐步发展，工业废水排放呈现下降的趋势，有必要持续增加废水治理的投入，使工业废水排放量严格控制在限制标准范围内；北部沿海地区工业废水排放量的增加能够在一定程度上推动区域经济发展，但长期来看这种影响会逐步减弱直至得到抑制；黄河中游地区作为钢铁工业和有色金属工业基地，经济增长带来工业废水排放量的增加，虽然这种影响也在缓慢减弱，但长期无法得到有效改善；西南地区是以旅游开发为重心的工业基地，人口流出性大，有效促进了工业废水排放的下降，在工业节水方面具有很大的进步空间；大西北地区的工业废水排放却对经济增长具有显著推动作用，短期内通过废水排放对经济产生正向促进效果，非长远之计，必须因水制宜，逐步减缓工业废水排放，改善水环境污染问题。

（3）工业废水排放对经济增长的预测方差贡献度比经济增长对工业废水排放的预测方差贡献度要小，这与当前社会发展现状相符合。因此，在考虑经济增长的同时，也要重视水环境污染问题，减少并严格控制工业废水排放，建立有效的水环境保护体系，开创双赢局面。